体验数形结合思想的功效

戴美红

【摘要】数形结合，主要指的是数与形之间的一一对应关系。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”“以数解形”、“数形转换”即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的效果。本文结合自己的教学实践阐述了如何使用教材对数形结合思想进行有效渗透，使学生逐步提高数形结合的能力。

【关键词】数形结合思想 转化 契合点

【中图分类号】G4 【文献标识码】A 【文章编号】2095-3089（2015）09-0124-01

新课标指出“使学生获得必要的数学基础知识和基本技能”是初中数学课程的目标之一。以下结合自己的教学实践，分别从引导学生直观感受基本的数学概念，亲身探究定理、结论产生的背景及应用等方面渗透数形结合思想，逐步提高学生的数形结合能力。在解决数学问题时，根据问题的条件和结论，使数的问题借助形去观察，而形的问题借助数去思考，采用这种“数形结合”来解决问题的策略，我们称之为“数形结合的思想方法”

数形结合的基本思路是：根据数的结构特征，构造出与之相适应的几何图形，并利用图形的特性和规律，揭示其几何意义，使数量关系和空间形式巧妙、和谐地结合起来，并充分利用这种结合寻找解题思路使问题得到解决。

在平时的解题过程中，我发现学生不易理解，解决不了的数学问题，往往是需要用数形结合来分析，比如学习了一段时间，要对这段时间的学习进行检测，进行检测的试卷中，当你认为哪些题目需要在班级进行讲解时，这些题目中，有60%是需要用数形结合来分析，从中我也意识到了数形结合思想在初中数学中的地位，因此我在这一轮的教学中，特别重视学生的数形结合思想的培养和转化，我认为它是一种非常好的方法，它——直观，形象。

教学中可以从以下两个方面，让学生在数学学习过程中，通过类比、观察、分析、综合、抽象和概括，形成对数形结合思想的的应用。

一、渗透数形结合的思想，养成用数形结合分析问题的意识

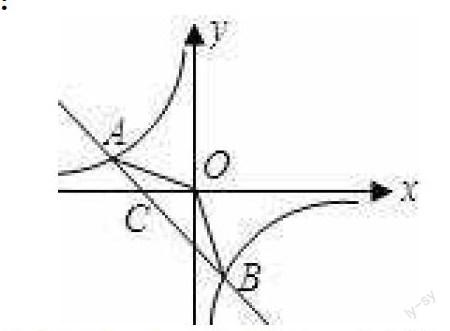
在学习九年级（上）第一章反比例函数的应用时，我设置了这样一道题：

1.如图，已知A（-4，n），B（2，-4）是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点.

（1）求反比例函数和一次函数的解析式；

（2）求直线AB与X轴的交点C的坐标及△AOB的面积；

（3）求方程kx+b-=0的解；

（4）求不等式kx+b-<0的解集.

学生当堂练，我拿着一支红笔站在学生旁边，时刻准备着给他们批阅，鼓励他们，看哪位，哪些先做好，我就先给他批，学生们劲头很足，但通过我这么观察和批阅下来，我发现学生之间的差距还是蛮大的，快的不到2分钟就做好，慢的要5分钟才好，出现这么大的差距，主要原因是学生与学生之间所用的方法不同导致的，归纳起来大体两类，平时习惯于用数形结合解决的，2分钟时间不到就好了，又快又准，平时用数形结合解题较少的同学，就在那里算，特别是第4小题，如果用计算的方法解决的话，那就要用到解一元二次不等式，初中阶段还没学到，基础好点的，知道对X要进行分类讨论，但耗的时间会很多，基础弱一点的，就不会想到分类讨论，这样就漏解。

在我观察，批阅，了解到学生的学情之后，我对这道题进行了点评，首先是通过这道题对那部分用数形结合又快又准得到答案的学生进行肯定和表扬，然后再用数形结合和学生一起分析这道题的过程，等我刚一讲完，我发现我们很多孩子在发出感叹，并且嘴里在说，“没想到通过图形去解决，那么方便，直接，数学结合方法真的很神奇”，这时让我感觉平时注重渗透数形结合思想是一种非常明智的做法。

二、学习数形结合思想，增强解决问题的灵活性，提高分析问题、解决问题的能力

在教学中渗透数形结合思想时，应让学生了解，所谓数形结合就是找准数与形的契合点，根据对象的属性，将数与形巧妙地结合起来，有效地相互转化，就成为解决问题的关键所在。

在八年级（下）第五章平行四边形的复习课中，我又设置了这样一道题：

2.在面积为15的平行四边形ABCD中，过点A作AE⊥直线BC于点E，作AF⊥直线CD于点F，若AB=5，BC=6，求CE+CF的值。

这道题我是以导学案形式发给学生的，它排在导学案中第8题（总共8题），当学生们做到这一题时，很自然的会想到画图，通过图形去解决，但是在画图的过程中，出现了很多小问题，主要表现在：1.AE，AF画成两条内高；2. AE，AF画成两条内高和外高，导致班级有两种错误的答案：；或；然后学生算出来是以上这两种错误答案之一时，他会认为自己是对的，没有更深入的重新思考，直到我过去批改、提醒时，才意识到自己的思考有错误，通过这道题也同时告诉我们要利用数学结合解决的题目很多时候是比较复杂的，因此在把图画好后，要通过图形回顾一下题目，是否和题目相吻合，这样才能体现利用数形结合方法的高效。

由以上的两个例子，我们可以看出数形结合思想的应用往往能使一些错综复杂的问题变得直观，解题思路非常的清晰，步骤非常的明了。另一方面在学生学习过程中，可以激发学生学习数学的兴趣。

利用现有教材，教学中着意渗透并力求帮助学生初步掌握数形结合的思想方法，结合其它数学思想方法的学习，注意几种思想方法的综合使用，给学生提供足够的材料和时间，启发学生积极思考。相信会使学生在认识层次上得到极大的提高，让学生更加热爱数学，感受数学的味道。

参考文献：

[1]《初中新学案优化与提高》天津科学技术出版社

[2]《全日制义务教育课程标准（实验稿）》北京师范大学出版社