某离心机模型辨识与仿真

牛宝良，陈洪

（中国工程物理研究院 总体工程研究所，四川 绵阳 621900）

加速度环境是各类飞行器必然遇到的一个环 境，它对飞行器的功能、结构有重要影响。为此，加速度环境试验成为一个重要的环境试验项目。比较便捷和常用的加速度试验设备是离心机。装备环境试验用的大型离心机采用臂式离心机，机臂由转轴驱动旋转，机臂的长臂一端安装被试产品。转轴由大型直流电机驱动，采用转速、电流双闭环控制。离心机控制系统最核心的功能就是控制离心机大臂转速，使得被试产品中心处的向心加速度逼近目标加速度。由于转动惯量、旋转风阻、摩擦阻力都是重要的影响因素，通过辨识来获取这些参数，能够得到最贴合实际的参数，对于进行系统仿真与分析具有重要意义。

直流调速系统仿真对于调速系统设计、分析和优化有重要作用，文献[1—5]介绍了基于Matlab/Simulink的直流调速系统仿真，采用一阶环节传函表达各模块，属于线性化模型。其中文献[3—4]同时建立了精细模型，对整流、电机部分采用了Powersim中的精细模块，可以获得更具体的电学仿真结果。文中建立了时域仿真模型，对一阶、二阶环节进行离散化，辨识出的阻力模型直接用时域模型，最后综合为一个完整的仿真模型。时域模型的主要优点是便于处理非线性，仿真快速。

文中介绍了基于中国工程物理研究院总体工程所某离心机的模型辨识、建模与仿真，基于辨识的参数，仿真结果接近真实试验。

1 离心机简介

某离心机为中国工程物理研究院总体工程所自主研制，主机如图1所示，主要参数：名义半径为7 m（转轴至吊篮中心）；最大负载质量为2000 kg（100g以下，g=9.8 m/s2）；最大加速度为200g，0.5g～200g无级调速；能力为200g-t，负载质量范围如图2所示。不装上下锥法兰，试件+夹具最大允许3500 kg。信号传输采用光纤旋转接头。此外配有适量的电功率环、电信号环、液压旋转接头供测试用。

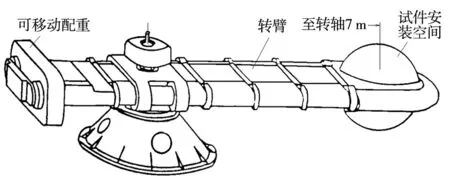
图1 离心机主体结构Fig.1 Diagram of the main structure of the centrifuge

图2 离心机负载质量曲线Fig.2 Load mass curve

3 参数辨识

3.1 试验数据

记录了4个工况的试验数据，分别是：空载，100g；空载，180g；负载1400 kg，100g；负载2106 kg，80g。每个工况记录了转速、励磁电流、电枢电流、电压时域数据。限于篇幅，给出了空载100g，2106 kg，80g两个工况实测数据的波形，如图3—5所示。

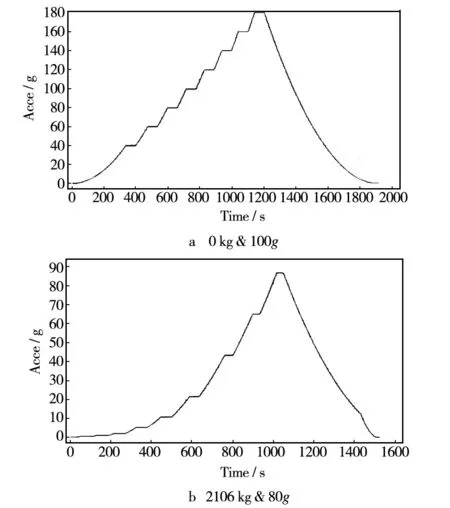
图3 加速度曲线Fig.3 Acceleration curve

3.2 参数拟合

图4 转速及其变化率曲线Fig.4 Speed and its changing rate curve

1）角加速度的拟合。角加速度是拟合等效转动惯量的重要参数。角加速度就是角速度的变化率，对角速度求导即可获得，但是这样直接计算的角加速度毛刺很大。这里采取的办法是对角加速度信号多次滤波，然后计算所有加速段的角加速度的平均值，然后由角加速度积分得到转速，根据积分转速与原转速波形的吻合程度再调整角加速度的平均值，直到两者完全吻合。得到结果见表1中的上升速率、下降速率。

图5 电流曲线Fig.5 Current curve

2）加速状态的电流-转速关系拟合。电机的驱动电流随着离心机加速或者保载状态而变，加速状态为克服惯性力矩，电流比较大。为拟合加速状态电流-转速关系，首先要从电流-时间曲线、转速-时间曲线中抽取出加速时的数据。以空载100g数据为例，从图4b可知，角加速度大约0.0201 rad/s2，用Matlab语句n1=find（x_jjsd＞0.01）可以找到所有处于加速状态的数据对应的序号，根据这个序号就可以提取出处于加速状态的电流、转速数据，见图6细线。用Matlab语句polyfit（x，y，2）就可以拟合到电流—转速多项式系数，x是电机转速，y是电流，2是指定的多项式阶次（试凑决定），拟合的曲线见图6a稍粗曲线。由于电流波动大，以第一次拟合的电流-转速曲线为基础，再筛选一次电流、转速数据，进行第二次拟合。拟合的曲线见图6a中的粗线，多项式见表1第三行。

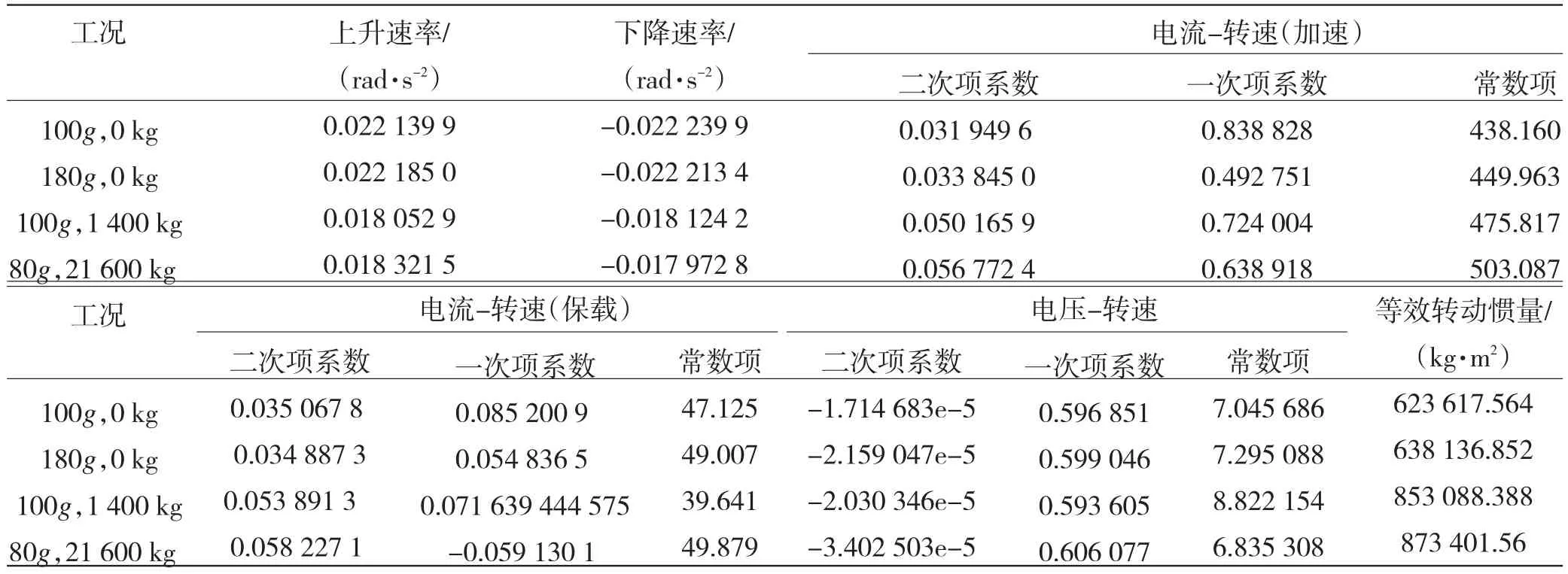
表1 辨识结果Table 1 Identification results

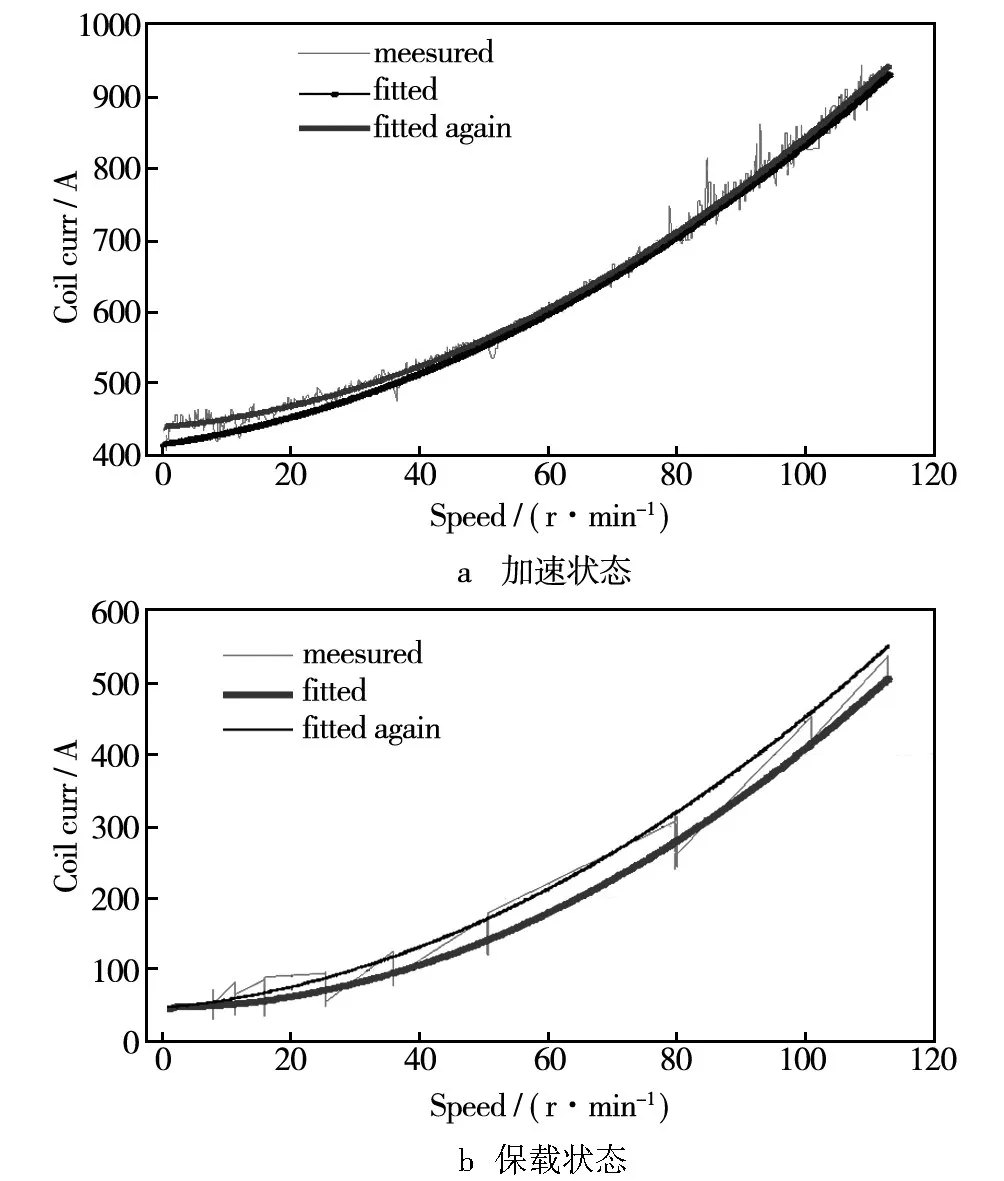
图6 实测、拟合的电流-转速曲线Fig.6 Measured and fitted current-speed curves

3）保载状态的电流-转速关系拟合。以空载100g数据为例，从图4b可知，角加速度大约0.02 rad/s2，用Matlab语句n1=find（x_jjsd＜0.01）可以找到所有处于保载状态的数据对应的序号。与加速状态的电流—转速拟合类似，也是进行2次拟合，拟合的曲线见图6b中的粗线，多项式见表1第四行。

4）等效转动惯量。离心机的重要参数之一是其等效转动惯量。效惯量就是把被试产品、机臂、转轴、电机等所有电机驱动的惯量折合为以主轴为转轴的惯量。以空载100g为例，在保载阶段，合力矩为0，阻力力矩与驱动力矩相等。根据拟合关系，转速为0时力矩为1 663.913 N·m。在加速阶段，根据拟合关系，转速为0时的驱动电流为438.160 9 A，对应力矩为15 470.804 N·m。加速时合力矩Mt=13 806.891 N·m，角加速度a=0.022 139 9 rad/s2，惯量J=Mt/a=623 617.564 kg·m2。

5）辨识数据的初步分析。等效转动惯量。基于空载100g，180g辨识的等效转动惯量为623 617.564，638 136.852，两者相差2.33%，在可接受范围。两个带载状态的等效转动惯量之间没有发现规律性的关系，这是因为影响因素比较多，包括试件、配重，配重半径等。作为仿真，不妨采用0～2106之间的线性预估，关系式为：

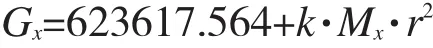
式中：Mx为试件质量，kg；Gx为等效转动惯量，kg·m2；k为系数，取2.42。

6）旋转阻力矩。保载电流与旋转阻力矩成比例，保载电流随转速的变化如图7a所示，空载的两条曲线非常接近，理应重合；负载1400，2106 kg的保载电流曲线有差异，说明负载质量对阻力矩有一定影响，但是影响不大。零转速时的电流分别是47.125，49.007，39.641，49.879 A，忽略离群的39.641，取49.007 A，对应的力矩是1730.363 N·m。此时风阻为0，主要克服摩擦阻力，即离心机的摩擦阻力矩为1730.363 N·m。风阻含有转速的一次项、二次项，一次项、二次项的系数随负载质量而变。

7）加速电流。加速电流随转速的变化如图7b所示，它包含了保载电流、惯量导致的电流，两个空载曲线基本重合，是合理的。不同负载质量下的电流曲线都不重合，正是反映了惯量因素。

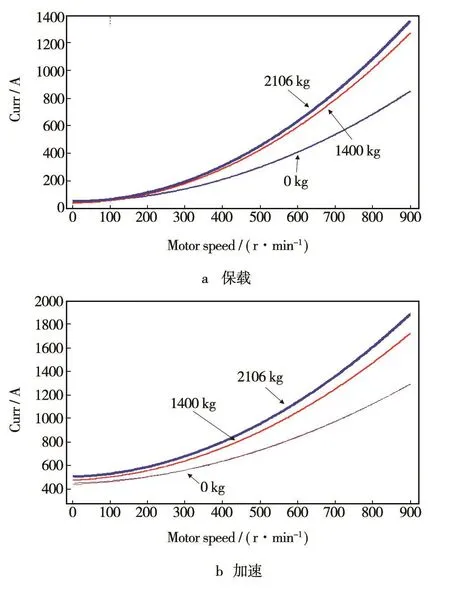
图7 保载电流、加速电流Fig.7 Currents at holding and speeding up

4 建模与仿真

4.1 离心机转速控制仿真模型

离心机转速控制采用双闭环直流调速，系统组成如图8所示，包括转速给定、转速PI控制器、电流PI控制器、电流放大器、直流电机及减速器、转臂、转速传感器、电流传感器等。仿真模型如图9所示，组成与图6相同。已有文献中的仿真模型多采用线性模型，也有同时采用线性模型、精细的电气模块模型两种模型的并进行比较。该模型采用时域仿真模型，原因有以下几点：控制器是基于PLC的，本身就是离散化PI控制器；时域模型可以表达像风阻这样严重的非线性特性；时域模型可以利用Matlab的Accelerator模式，仿真速度比Normal模式快若干倍；数据步长统一。这里重点介绍其中的电流放大模块、转臂运动模块。

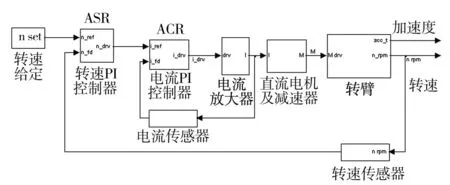
图8 离心机转速控制系统Fig.8 System block diagram of centrifuge speed control

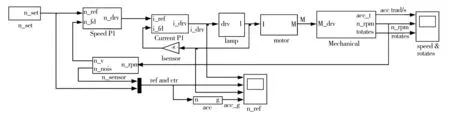
图9 离心机转速控制系统仿真simulink模型Fig.9 Simulink model of centrifuge speed control system

1）电流放大模块。三相全控桥式50 Hz，时间常数为0.0033 s，因此用一个时间常数0.0033 s的一阶环节来表示。比例系数是最大电流1455 A/10 V，此外加了一个饱和模块，饱和限是-1455，1455 A。

2）转臂模块。如图10所示，转臂模块反映了转臂在合力矩驱动下产生角加速度、转速。合力矩由电机驱动力矩、阻力矩合成，阻力采用上述拟合的阻力模型，并施加了少量随机成分，如图11所示。

图10 离心机转臂转动simulink模型Fig.10 Simulink model of centrifuge arm rotation

4.2 离心机转速控制仿真

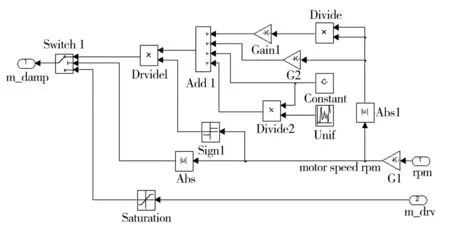
图11 离心机转臂阻力矩Simulink模型Fig.11 Simulink model of centrifuge arm damp moment

仿真算例，负载1400 kg，最高加速度为142g，保载60 s，上升过程的几次保载量级及持续时间与实际试验时一致。目的是了解200g-t的可实现性和不同控制方法抑制超调的效果。上升速率在0.14 rpm/s以下，可以达到200g-t，更高上升速率电流将会超极限1455 A。纯P控制，设置142g，实际达到138.85g，采取预补偿，达到142g且无超调。图12显示了仿真结果，依次是电流控制器输出、转速、电流、加速度波形。还可以获得驱动功率、风阻功率、转速控制器输出等更多内部信息，限于篇幅不做介绍。

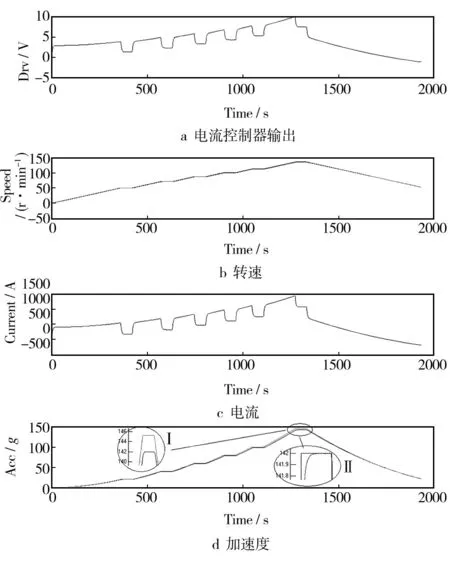
图12 1400 kg，142g仿真结果Fig.12 Simulink result of 142g，1400 kg load

4.3 关于超调

许多直流调速系统希望把超调控制在小范围，加速度试验也是一样。为消除静差，速度调节器常采用PI控制，I的加入就带来超调，如何控制超调，这里提出三个办法。

1）在给定信号后加一个低通滤波器。事实上有许多仿真模型或者系统框图有这个滤波器，但是其出发点是让参考信号与反馈信号经过同样滤波。这里主要是为了让上升段与平直段交点处平滑一些，减小交点处的超调量。此外，I增益参数尽量小。

2）采用P控制，不会有超调，但是有静差。先仿真一次，目标加速度a0，实际达到加速度a1，对应的转速分别是n0，n1，把目标转速设置为n0（n0/n1），再仿真或者直接用于试验，就可消除静差，且无超调。图10显示了这种方法的效果，加速度波形的局部放大图（图12dⅠ）可见预补偿后的实际加速度达到142g目标值且无超调。这个办法特别适合保载时间短（1 min以内）的试验，也可用于长时间试验。

3）如果是数字控制，把速度调节器中的积分输入设计成可切换的，保载时切入正常，其他情况积分输入为0，只是在保载阶段让积分用于消除静差，仿真效果如图12d中Ⅱ所示。I增益可以取大一些。

5 结论

文中基于离心机运行时的数据，辨识了离心机惯量、风阻等关键参数，为仿真分析奠定了基础。建立了基于Simulink的时域仿真模型，模型运行快速，仿真结果与实际运行结果相近，说明所建模型比较可信，可用于控制参数的优化。基于模型，对预期的试验量级进行仿真，可为判断系统能力提供参考。基于模型仿真，研究了超调问题，利用仿真结果进行加速度预补偿或者采用可切换积分，可实现无超调精确控制。

[1] 徐月华，汪仁煌.Matlab在直流调速设计中的应用[J].微计算机信息，2003，19（8）：32—33.XU Yue-hua，WANG Ren-huang.The Application of Matlab in Design of DC Speed Regulation[J].Micro Computer Information，2003，19（8）：32—33.

[2] 钮王杰，张斌超，刘春艳.基于MATLAB/Simulink转速闭环直流调速控制系统的仿真研究[J].山西大同大学学报（自然科学版）2011，27（5）：33—35.NIU Wang-jie，ZHANG Bin-chao，LIU Chun-yan.Research of Speed Closed-loop DC Speed Control System Simulation Based on Matlab/Simulink[J].Journal of Shanxi Datong University（Natural Science），2011，27（5）：33—35.

[3] 刘春艳，闻玉凤.基于MATLAB/Simulink双闭环直流调速系统的仿真研究[J].山西大同大学学报（自然科学版）2014 ，30（3）：26—28.LIU Chun-yan，WEN Yu-feng.Research of Double-loop DC Speed System Simulation Based on Matlab/Simulink[J].Journal of Shanxi Datong University（Natural Science），2014 ，30（3）：26—28.

[4] 董德智，孙驷洲.Matlab在双闭环直流调速控制系统教学中的应用[J].自动化与仪器仪表，2007（4）：40—43.DONG De-zhi，SUN Si-zhou.The Application of Matlab in Teaching of Double-Loop DC Speed regulation[J].Automation and Apparatus，2007（4）：40—43.

[5] 刘翔，曹萍，陈致远，等.直流调速系统与Matlab仿真[J].电气传动2013，43（4）：12—16.LIU Xiang，CAO Ping，CHEN Zhi-yuan，et al.DC Speed Control system and Simulation with Matlab[J].Electric Dive，2013，43（4）：12—16.