精密离心机结构误差对其运动精度的影响研究

王洪波，张映梅，李锋，卢永刚

（中国工程物理研究院 总体工程研究所，四川 绵阳 621900）

精密离心机是校准和标定高精度惯性仪表的大型高精密测试设备，其自身的精度直接决定了惯性仪表的校准和标定精度。精密离心机的主轴速率精度、径向误差、倾角误差是影响离心机系统精度的主要因素。国内外学者针对主轴回转误差对精密离心机系统精度的影响开展了大量研究[1—3]。文献[4]介绍了各种误差源对离心机精度的影响，如由不平衡力引起的主轴圆锥运动，但精密离心机回转精度对其向心加速度和失准角的影响分析尚不够充分。任顺清等[5—6]分析了主轴一次谐波误差对离心机瞬时工作半径的影响，提出在主轴上下两个截面上安装4个位移传感器测试主轴回转精度，克服了以往不能测试一次谐波误差的不足。

黎启胜等[7]研究了精密离心机结构安装误差对主轴回转精度的影响，建立了精密离心机结构安装误差对静压气体轴承主轴回转精度影响的计算模型。杨亚非等[8—9]指出在精密离心机上进行加速度计测试和标定时，加速度计的安装姿态误差和精密离心机主轴姿态误差是影响加速度计测试和标定准确度的重要因素，并重点分析了误差中偏载质量对系统精度的影响。李树森等[10]把描述气体轴承工作的雷诺方程与转轴动力学方程合并，采用直接数值求解方法分析了精密离心机静压气体轴承-转轴系统在不平衡力作用下主轴的稳定性情况，以及对主轴系统运动精度的影响，对旋转主轴的稳定性进行了理论分析和数值求解，给出了稳定性的判定条件和稳定区域范围。

国内外学者主要采用解析方法研究精密离心机主轴回转系统的运动精度。解析方法一般将复杂的机械系统简化，忽略了其中众多的影响因素。多体动力学仿真能更加真实地再现复杂机械系统的运动，具有精度高、计算周期短等优势。因此，文中基于LMS Virtual.Lab Motion多体动力学仿真软件，建立精密离心机主轴回转系统的运动模型，研究其结构误差对主轴回转系统运动精度的影响规律。

1 精密离心机多体动力学仿真模型

一种盘式高精度静态离心机，主要包括空气轴承、负载盘、连接体、电机、基座等部件。离心机工作时其主轴回转系统由负载盘、空气轴承轴套、连接体、电机转子等组成。利用多体动力学分析软件，建立精密离心机机械系统仿真模型，针对精密离心机结构复杂，且具有高精度要求，通过对关键零部件进行精确建模，对于复杂且次要构件在保证其质量、惯量等特性的前提下进行简化，静压气体轴承通过LMS Virtual.Lab Motion中衬套力定义空气轴承的刚度、阻尼实现，模型如图1所示。

2 精密离心机多体动力学仿真分析

2.1 主轴回转系统静不平衡量的影响

图1 精密离心机多体动力学仿真模型Fig.1 Simulation model of precision centrifuge

在精密离心机模型上一固定偏心距位置施加偏心质量块，通过改变偏心质量块的质量来分析不同静不平衡量对主轴回转系统半径误差和倾角误差的影响。

图2 主轴回转系统半径误差和倾角误差随静不平衡量的变化Fig.2 Rotary error of main shaft versus the plate eccentricity error relative to aerostatic bearing axes

高精度静态精密离心机的恒线性加速度范围为：1g～100g[7]。选取4种加速度，分别是1g，20g，60g和100g（对应转速分别为27.9，124.7，216.0，278.9 r/min）。在不同加速度下静不平衡量对主轴回转系统半径误差和倾角误差的影响如图2所示，可以看出，不同转速条件下，主轴回转系统的半径误差随静不平衡量的增加线性增大。当转速较小时，半径误差随静不平衡量的增大增长得非常缓慢；当转速逐渐增加时，半径误差随静不平衡量的增大增长逐渐明显。在上述静不平衡量变化范围内，半径误差最大只有0.497 μm。不同转速下，主轴回转系统的倾角误差非常小，随着转速的增加呈线性增长，且转速越大增长越明显，这与文献[7]理论分析的结果一致。

图3给出了转速为278.9 r/min，静不平衡量为1.70 kg·m时，主轴回转系统的运动响应。主轴回转系统质心在x轴和y轴方向的位移随时间的变化曲线如图3a，b所示，在给定的转速下，回旋系统质心的位移分量稳定变化。图3c为主轴回转系统绕轴承中心线的运动轨迹，表现为当回转系统受到静不平衡量的扰动时，质心由初始的位置偏移一定半径误差后，开始以此半径作稳定的圆周运动。图3d为回转系统倾角误差随时间的变化曲线，可以看出，主轴回转系统偏离中轴线后，以一固定的角度作圆锥运动，该角度非常小，可近似认为回转系统作圆周运动。

图4给出了不同静不平衡量下主轴回转系统半径误差、倾角误差沿主轴轴向的变化规律。可以看出，对于某一固定静不平衡量，主轴回转系统的半径误差沿轴向基本没有变化。随着静不平衡量的增加，主轴回转系统的半径误差逐渐增加。同样，对于某一固定静不平衡量，主轴回转系统倾角误差沿轴向基本没有变化。当静不平衡量增加时，倾角误差随之增加，由于倾角误差本身非常小，其增加不明显。在选取的轴向位置范围内，对于某一固定工况半径误差基本没有变化，倾角误差非常小，因此主轴回转系统基本作近似圆周运动。

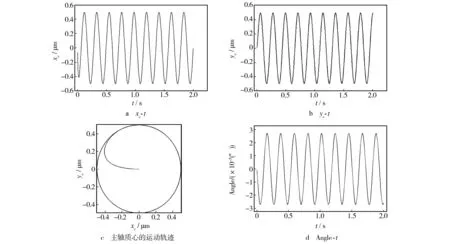
图3 主轴回转系统的响应（n=278.9 r/min，Δm·μ=1.70 kg·m）Fig.3 Response ofthe rotary precision of main shaft at n=278.9 r/min，Δm·μ=1.70 kg·m

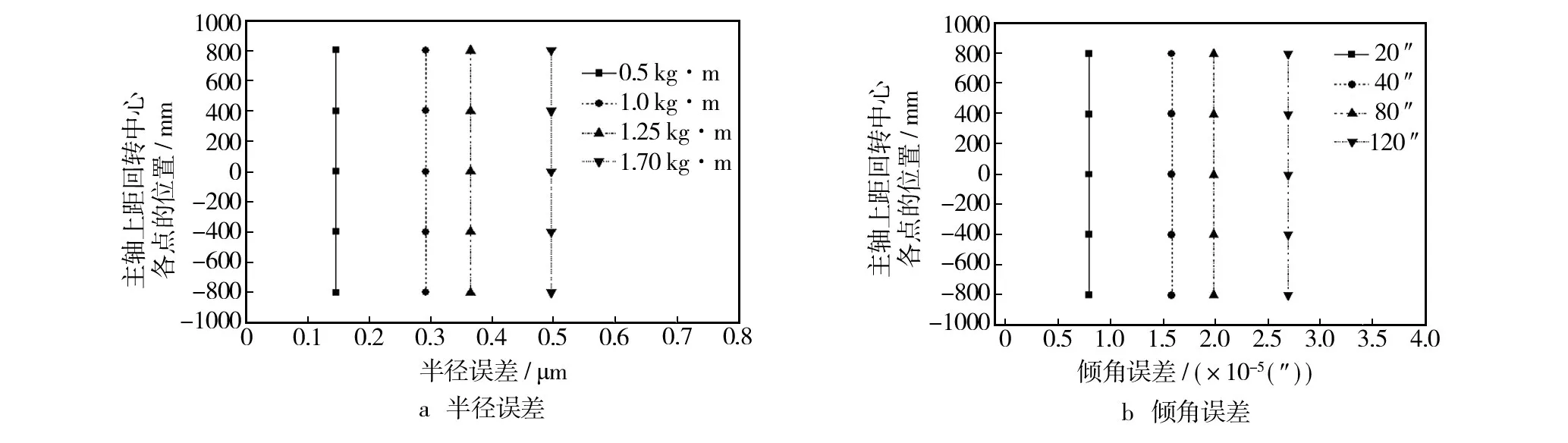
图4 主轴半径误差和倾角误差沿主轴的变化规律Fig.4 Rotary error of main shaft versus location of main shaft

2.2 主轴铅垂度误差的影响

文献[7]给出了主轴回转运动分析模型，主轴铅垂度误差引起的附加力矩和附加力可用方程（1），（2）表示：

由式（1）和式（2）可知，主轴铅垂度误差引起的附加力矩和附加力均与主轴回转系统的转速无关，因此主轴铅垂度误差引起的半径误差和倾角误差也与主轴回转系统的转速无关。通过给定不同的主轴铅垂度误差，在精密离心机模型上施加相应的附加力矩和附加力，分析主轴铅垂度误差对主轴回转系统半径误差和倾角误差的影响，如图5所示。

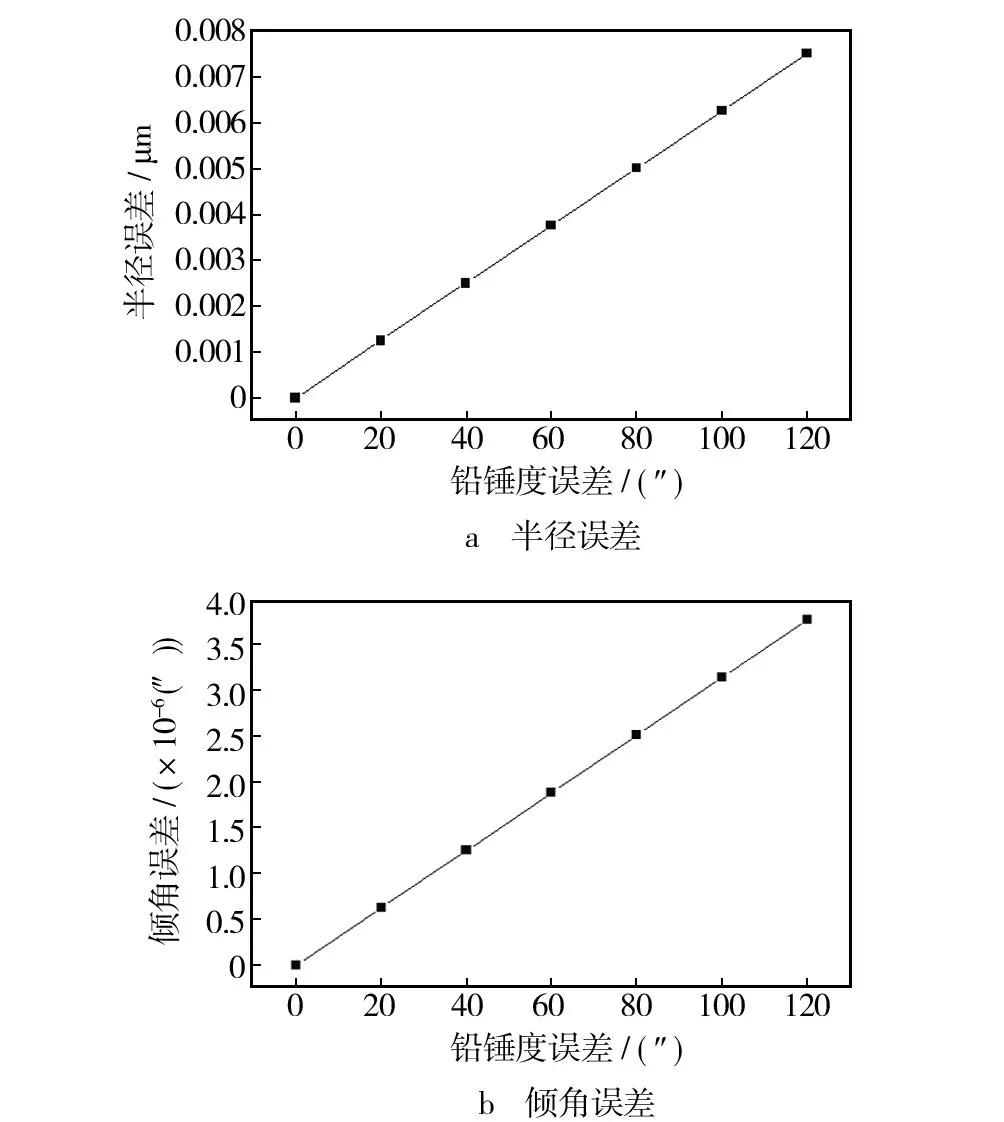
图5 主轴回转系统半径误差和倾角误差随铅垂度误差的变化关系Fig.5 Rotary error of main shaft versus the plumb assembly error of aerostatic bearing axes

分析发现，主轴回转系统半径误差、倾角误差随主轴铅垂度误差的增加线性增加。当主轴铅垂度误差为120″时，半径误差只有0.0075 μm，倾角误差只有3.8158e-6″。相对于静不平衡量对主轴回转系统半径误差和倾角误差的影响，主轴铅垂度误差的影响较小。

2.3 转盘与主轴安装垂直度误差的影响

由于转盘与主轴安装垂直度误差δ引起的附加力为0，附加力矩为[7]：

由惯性积的旋转变换规律得[11]：

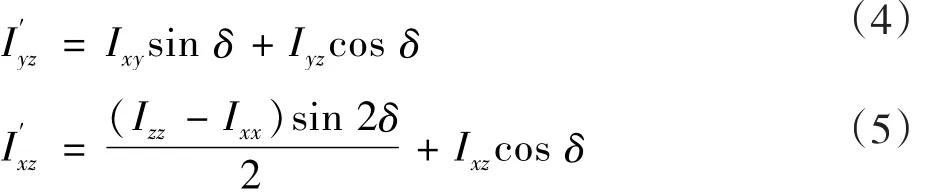
式中：Izz，Ixx分别为转盘与主轴垂直度误差为0时对z轴、x轴的惯性矩；Ixy，Iyz，Ixz分别为转盘与主轴垂直度误差为0时对坐标系o1xy中x轴及y轴、y轴及z轴、x轴及z轴的惯性积。

由于文中只考虑主轴回转系统以某一恒定转速旋转过程中转盘与主轴安装垂直度误差δ对主轴回转系统运动精度的影响，因此垂直度误差δ引起的附加力矩为：

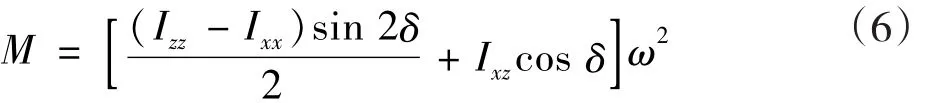
通过不同转速条件下给定不同的转盘与主轴安装垂直度误差，获得不同的附加力矩。在精密离心机模型上施加相应的附加力矩，分析不同垂直度误差对主轴回转系统半径误差和倾角误差的影响，如图6所示。

不同转速下，主轴回转系统半径误差和倾角误差随垂直度误差的增加线性增大。随着主轴回转系统转速的增加，其半径误差和倾角误差受垂直度误差的影响越来越明显，但在垂直度误差的变化范围内，最大半径误差为9.484e-5 μm，最大倾角误差为1.2561e-5″。

图7给出了不同垂直度误差下主轴回转系统半径误差和倾角误差沿主轴轴向的变化规律。可见，对于某一固定垂直度误差，在选取的轴向位置范围内，主轴回转系统的半径误差随轴向位置的升高逐渐增加，而倾角误差沿轴向位置没有明显变化。当垂直度误差增加时，主轴回转系统的半径误差和倾角误差沿着轴向位置依次增加。即随着垂直度误差的增加，主轴回转系统的圆锥运动越来越明显。

2.4 主轴回转系统静不平衡量、铅垂度误差和垂直度误差的综合影响

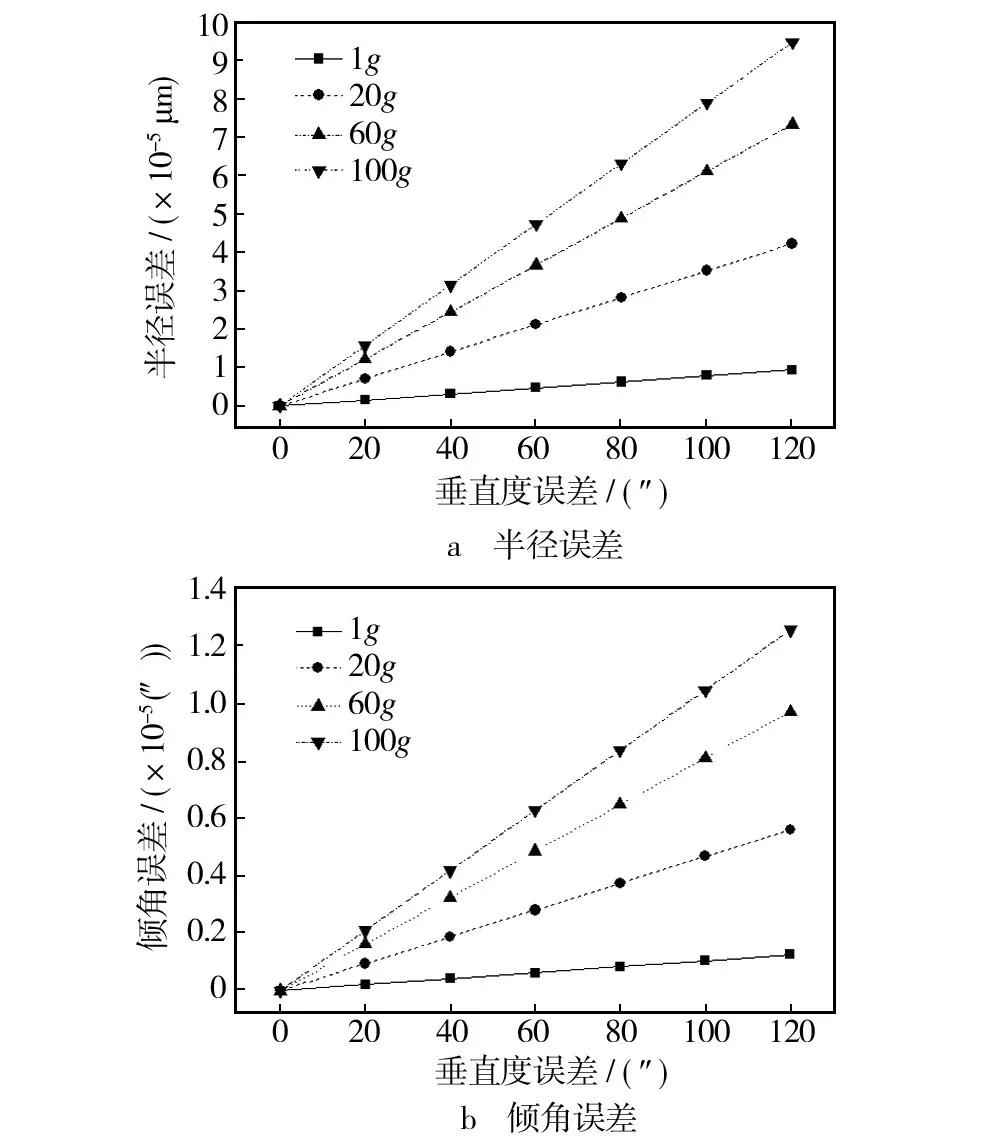
图6 主轴回转系统半径误差和倾角误差随垂直度误差的变化关系Fig.6 Rotary error of main shaft versus the plate perpendicularity error relative to aerostatic bearing axes

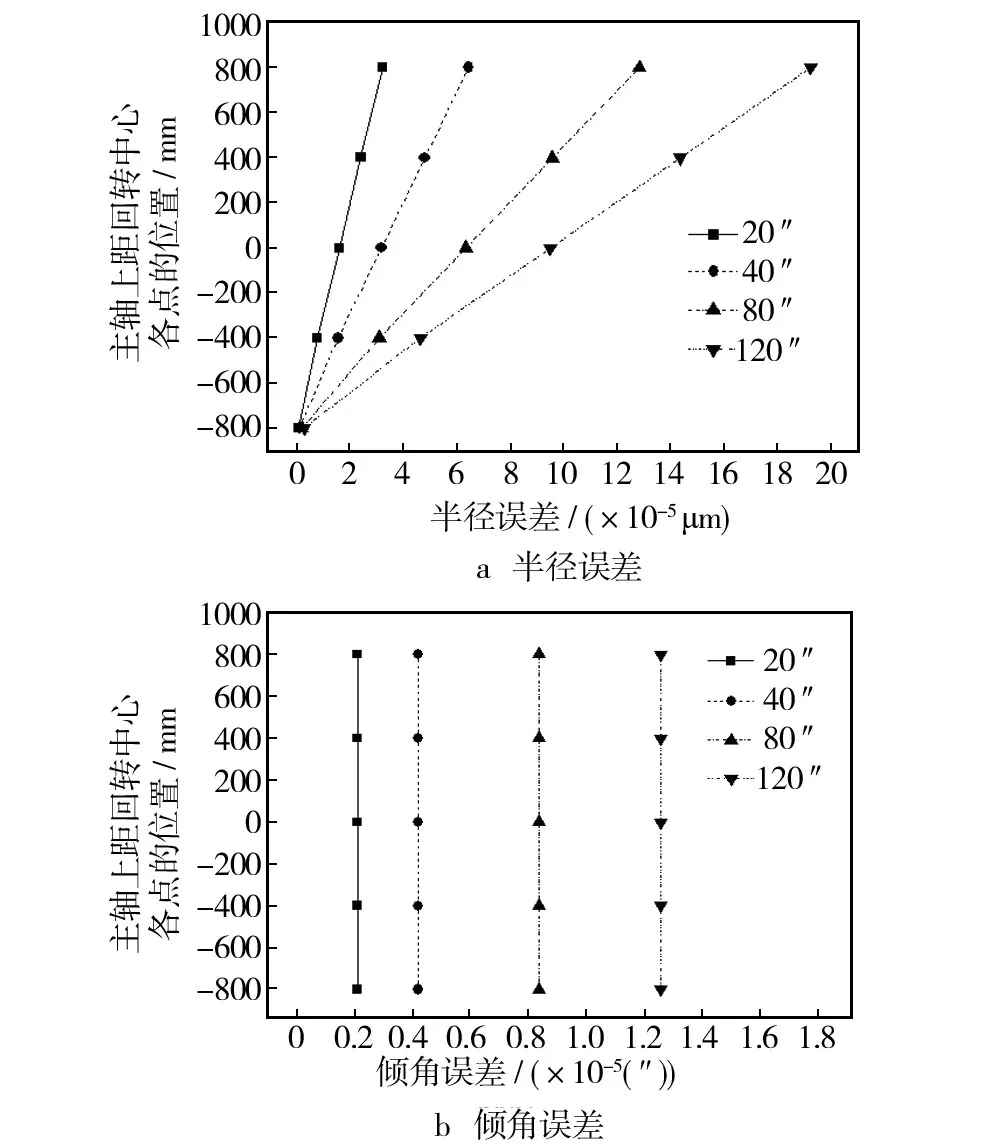
图7 主轴回转系统半径误差和倾角误差沿轴向的变化规律Fig.7 Rotary error of main shaft versus location of main shaft

采用278.9 r/min高转速，分析静不平衡量、铅垂度误差和垂直度误差对主轴回转系统半径误差和倾角误差的影响规律。图8和图9分别给出了主轴回转系统半径误差、倾角误差随着静不平衡量、铅垂度误差和垂直度误差的变化规律。

图8 半径误差随着静不平衡量、铅垂度误差和垂直度误差的变化规律Fig.8 Rotary error of main shaft versus the plate eccentricity error and the plumb assembly error as well as the plate perpendicularity error

由图8可知，不同铅垂直度误差、不同静不平衡量条件下，半径误差随垂直度误差的增长不是很明显。静不平衡量对主轴回转系统半径误差的影响在三个结构误差中占主导，铅垂度误差影响次之，垂直度误差影响相对最小。

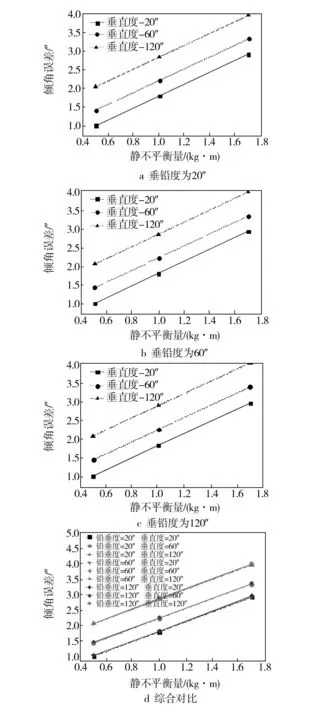
图9 倾角误差随着静不平衡量、铅垂度误差和垂直度误差的变化规律Fig.9 Rotary error of main shaft versus location of main shaft the plate eccentricity error and the plumb assembly error as well as the plate perpendicularity error

从图9可见，在一定的铅垂度误差和垂直度误差下，主轴回转系统的倾角误差随静不平衡量的增加线性增加；在一定的铅垂度误差和静不平衡量条件下，主轴回转系统的倾角误差随垂直度误差的增加而增加；在一定的垂直度误差和静不平衡量条件下，主轴回转系统的倾角误差随铅垂度误差增加不明显。综合三个结构误差对主轴回转系统倾角误差的影响分析发现，静不平衡量、垂直度误差对主轴回转系统倾角误差的影响占主导，而铅垂度误差影响次之。

3 结论

基于LMS Virtual.Lab Motion多体动力学仿真软件，分析了主轴回转系统静不平衡量、静压气体轴承主轴的铅垂度误差和转盘与静压气体轴承主轴的垂直度误差，以及各结构误差共同作用对主轴回转系统的半径误差和倾角误差的影响规律，结论如下：

1）随着主轴回转系统静不平衡量、铅垂度误差和垂直度误差的增大，主轴回转系统的半径误差和倾角误差均线性增加。

2）在静不平衡量、铅垂度误差和垂直度误差对主轴回转系统运动精度的综合影响下，静不平衡量对主轴回转系统半径误差的影响占主导，铅垂度误差影响次之，垂直度误差影响相对最小；对于主轴回转系统倾角误差，静不平衡量、垂直度误差的影响占主导，而铅垂度误差影响次之。

[1] REDDI M M，CHU T Y.Finite Element Solution of the Steady Stale Compressible Lubrication Problem[J].Journal of Lubrication Technology，1970，92（2）：495—503.

[2]WADHWA S S.Analysis of Externally Pressurized Gas Bearings By an Incremental Finite Element Method[J].Wear，1981，69（2）：133—141.

[3] CASTELLI V，PIRRICS J.Review of Numerical Methods in Gas Bearing Fnm Analysis[J].ASME，1968，90（4）：777—792.

[4] IEEE Std 836—2001，IEEE Recommended Practice for Precision Centrifuge Testing of Linear Accelerometers[S].

[5] 任顺清，杨亚非，吴广玉.精密离心机主轴回转误差对工作半径的影响[J].哈尔滨工业大学学报，2000，32（1）：54—57.REN Shun-qing，YANG Ya-fei，WU Guang-yu.Effect of Rotational Error of Precision Centrifugal Main Axle on Working Radius[J].Journal of Harbin Institute of Technology，2000，32（1）：54—57.

[6] 任顺清，陈岩，赵振昊.精密离心机主轴回转误差对加速度计输入精度的影响[J].中国惯性技术学报，2007，15（1）：116—119.REN Shun-qing，CHEN Yan，ZHAO Zhen-hao.Influence of Rotary Errors of Centrifuge Spindle on Accelerometer Input Accuracy[J].Journal of Chinese Inertial Technology，2007，15（1）：116—119.

[7] 黎启胜，张映梅，卢永刚，等.精密离心机结构安装误差对主轴回转精度的影响[J].机械设计与制造，2012（2）：5860.LI Qi-sheng，ZHANG Ying-mei，LU Yong-gang，et al.Effect of Assembly Error of Precision Centrifuge Structure on Rotary Precision of Main Spindle[J].Machinery Design&Manufacture，2012（2）：5860.

[8]杨亚非.精密离心机上加速度计安装姿态误差和主轴姿态误差对测试的影响[J].宇航计测技术，2002，22（4）：30—34.YANG Ya-fei.The Influence of Accelero-meters Fixing Attitude Errors and Main-axis Attitude Errors on Acceler-ometers Test on the Precision Centrifuge[J].Journal of Astronautic Metrology and Measurement，2002，22（4）：30—34.

[9] 杨亚非.动不平衡对离心机精度的影响[J].测试技术学报，2008，22（2）：95—98.YANG Ya-fei.Influence of Dynamic Unbalance on Centrifuge Accuracy[J].Journal of Test and Measurement Technology，2008，22（2）：95—98.

[10]李树森.精密离心机静压气体轴承主轴系统动力学稳定性研究[D].哈尔滨：哈尔滨工业大学，2002.LI Shu-sen.Research on the Stability of Pressurized Bearing of the Precision Centrifuge Centrifuge[D].Harbin：Harbin Institute of Technology，2002.

[11]郭茂政.论惯性积的平移变换和旋转变换[J].大学物理，2004，23（6）：23—31.GUO Mao-zheng.A Discussion on the Shifting Transformation and Rotating Transformation of Inertial Prouduct[J].College Physics，2004，23（6）：23—31.