联轴器刚度对离心机转速稳定性的影响

陈文颍，宋琼，洪建忠

（中国工程物理研究院 总体工程研究所，四川 绵阳 621900）

离心机系统结构中，在驱动系统与主体旋转结构之间需要通过动力传递装置进行连接。除少数采用电机转子——离心机主轴整体设计的特殊系统之外，常规离心机一般采用联轴器作为动力传递器件。根据联轴器是否包含弹性组件及扭转刚度的不同，可分为弹性联轴器与刚性联轴器两类，而不同大小的扭转刚度直接影响着系统性能。

转速稳定度是多数离心机设备的主要性能指标之一，不同类型的离心机设备对转速稳定度指标的要求不尽相同，如精密离心机将其作为核心参数[1]，而例行实验离心机与土工离心机则要求尽量兼顾转速稳定度指标。离心机的转速稳定度指标受到来自伺服驱动系统内部与外部扰动扭矩双重作用的影响。其中，内部扰动扭矩由离心机伺服驱动系统的转速环测速误差、电流环输出偏差、以及驱动电机固有转矩脉动等因素引起，其通过动力传递装置传输到系统旋转惯量后影响离心机的转速稳定度[2—3]；外部扰动扭矩则由离心机旋转时受到的非线性扰动扭矩组成（包括风阻波动、轴承阻力波动等）[4]，其影响可由伺服驱动系统通过闭环控制生成对应的调整扭矩进行抑制。

联轴器由于扭转刚度的不同具有不同的力传导频率响应特性[5]，刚度越高的联轴器力传导频响也越高，有助于伺服驱动系统调整扭矩的传输；刚度较低的联轴器力传导频响也较低，故能够滤除部分来自伺服驱动系统的内部扰动扭矩。文中以Matlab/Simulink数学仿真软件为工具，通过建立包含联轴器扭转刚度及阻尼特征模块的离心机转速伺服控制系统仿真模型，分析了联轴器扭转刚度对离心机系统转速稳定性的影响。

1 离心机伺服驱动系统数学模型

常规离心机的伺服驱动系统一般采用转速环——电流环的双层闭环控制结构，其转速控制过程的基本原理如图1所示[6]。向其所示的伺服控制结构中引入联轴器模拟环节，基于达朗伯原理的一个典型联轴器动力传递过程可由如下动力方程进行表述（忽略轴承摩擦阻尼）[7—8]：

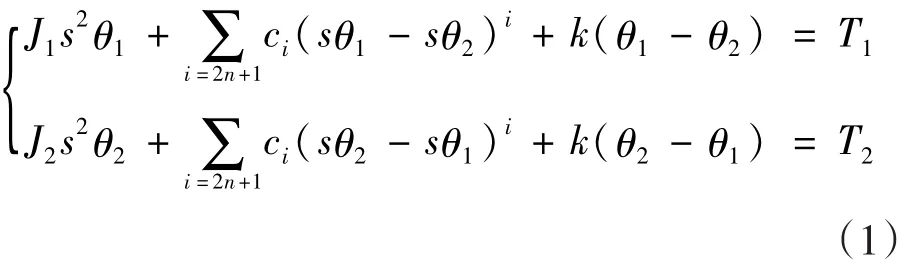
式中：J1，J2为驱动系统与被驱动系统的转动惯量，且J=J1+J2；T1，T2为驱动系统与被驱动系统的扭矩及阻扭矩，且 Te=T1-Tin，T2=TL；θ1，θ2为联轴器两端驱动系统与被驱动系统的转动角，且ωrm=sθ1或sθ2（由转速传感器的安装位置决定）；k，ci分别为联轴器的扭转刚度与第i阶扭转阻尼系数；s为微分算子。由此可得整合了联轴器结构的伺服驱动系统控制过程的数学表达式，如式（2）—（5）所示，其中Δωrm为系统转速测量误差：

2 联轴器刚度对离心机转速稳定性的理论分析

分析式（3）—（5）可知，离心机伺服驱动系统一方面将根据测速结果与转速指令的差值成调整扭矩，用于对抗扰动扭矩；另一方面还会因转速测量误差Δωrm产生系统自生扰动扭矩影响系统转速；此外拖动电机还不可避免地存在固有转矩脉动，并构成了驱动系统内部扰动扭矩Tin的主要成分。

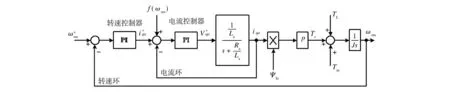
图1 伺服驱动系统原理Fig.1 The principle diagram of the servo drive system

综上所述，以提升离心机系统转速稳定度为目标，联轴器的设计选型显然期望其既能够滤除伺服驱动系统自生及内部的扰动扭矩——即选用刚性较低的联轴器，又能够有利于调整扭矩的传递——即选用刚性较高的联轴器。因此，离心机系统对联轴器的设计选型必须综合联轴器的扭矩传导频响特性、系统扰动扭矩组成与系统实际工况等因素。由此可得，典型离心机系统结构中（联轴器两端分别连接拖动电机转子与系统负载，拖动电机产生的扭矩经电机转子—联轴器—系统负载完成力传递过程），在忽略外界扰动扭矩TL及高阶扭转阻尼的影响后，联轴器两端的输出扭矩T与输入扭矩Te+Tin的关系表达如式（6）所示：

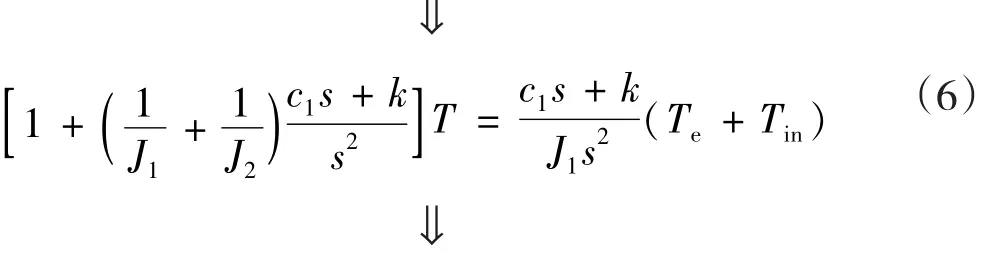
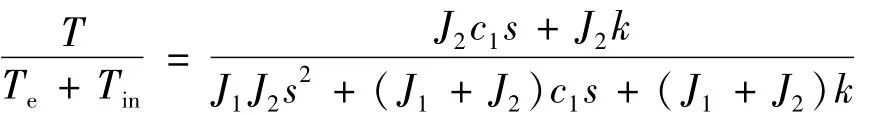
由此联轴器的扭矩传导频响特性可等效为一个二阶滤波器，基于典型滤波器参数计算公式可计算出其对应截止频率Fr（单位：Hz）如式（7）所示[9]。联轴器的扭矩传导频响范围随其扭转刚度k的增大逐渐变宽，且成0.5次方正比关系；并受到联轴器两端转动惯量的共同影响，且与之成近似0.5次方反比关系。

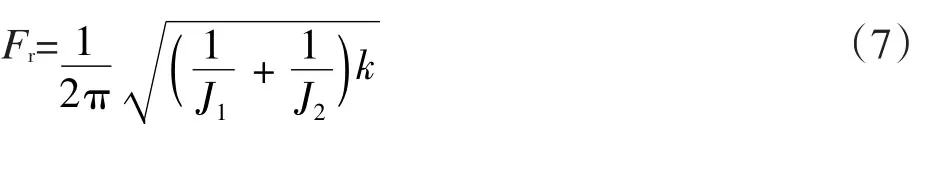
由于离心机系统中联轴器在面向扭矩传输功能时的滤波器特性，可认为联轴器的设计选型决定了伺服驱动系统的最高调速频率，其越大系统的动态性能越好，反之系统则具备更好的稳态性能），即决定了离心机系统的动稳态性能——当调速扭矩频率大于联轴器扭矩传导截止频率Fr时，其对系统负载的影响将逐渐降低直至归零。

3 系统仿真

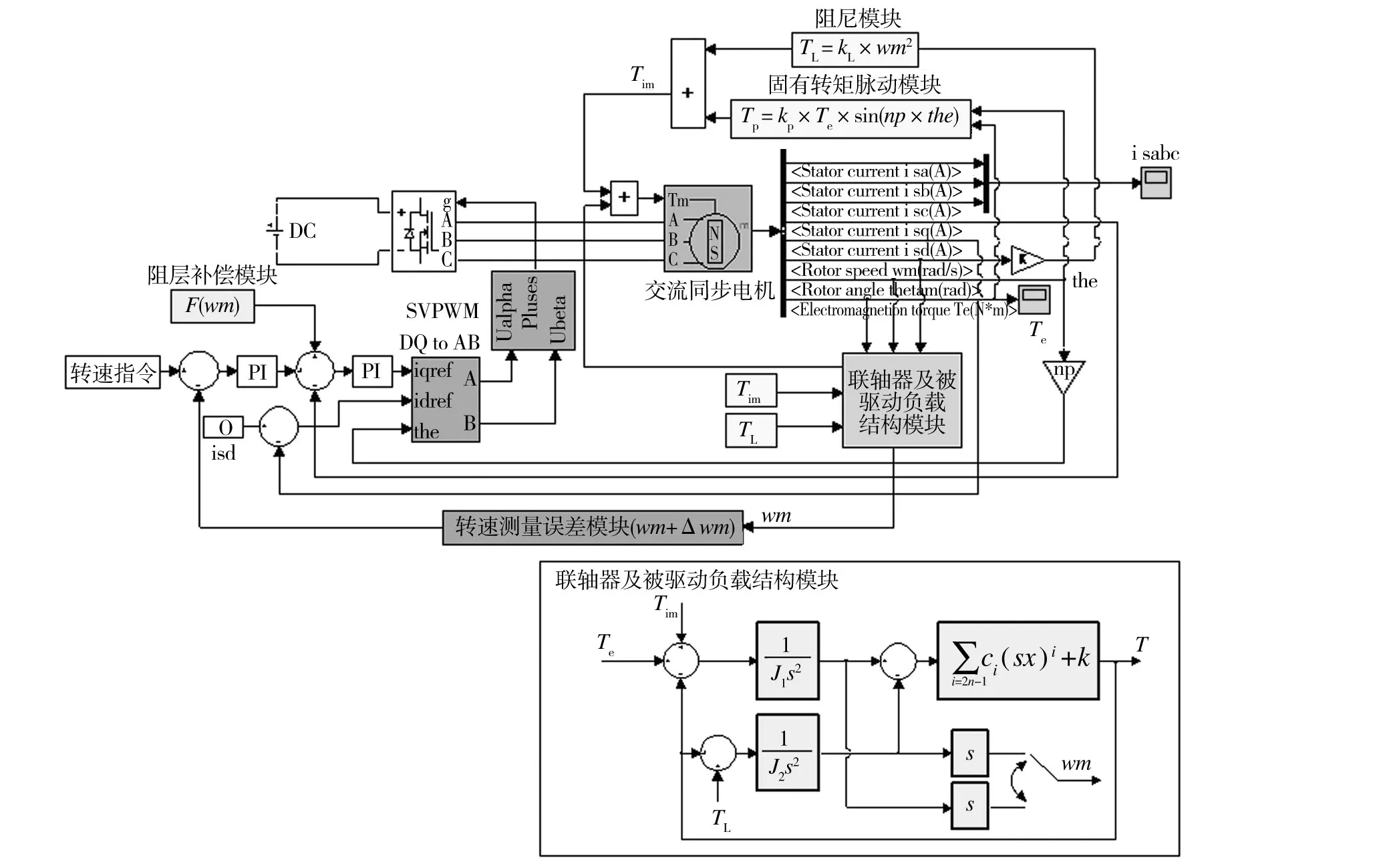
图2 离心机伺服驱动系统仿真模型Fig.2 The simulation model of the centrifuge servo drive system

基于上述离心机伺服驱动系统的原理结构与联轴器动力传递过程公式，并结合离心机系统中常用的矢量控制交流同步电机方案，建立如图2所示的整合了联轴器结构的离心机伺服驱动系统Matlab/Simulink数学仿真模型，并利用联轴器扭转刚度对离心机系统转速稳定性的影响开展仿真分析。

该仿真模型在整合了联轴器结构的基础上，由转速环、阻尼补偿模块、电流环、坐标变换模块、SVPWM模块、三项逆变器、同步电机组成，并考虑了转速测量误差、电流环固有输出偏差、扰动扭矩等干扰因素对系统输出转速的影响，能较为精确地模拟离心机的运转过程及其中各类非线性因素。

使用该数学模型进行仿真，分析联轴器的扭转刚度对离心机转速稳定度的影响。基于某动态离心机系统为原型设计仿真模型参数：驱动惯量为2.5 kg·m2，被驱动惯量为100 kg·m2，拖动电机转矩常数为15 N·m/A，系统额定输出扭矩为300 N·m等。

针对扰动扭矩的不同来源构造以下两类仿真目标——以伺服驱动系统的自生及内部扰动扭矩为主的离心机设备，对应外界扰动扭矩TL的绝对值期望为2 N·m，系统内部扰动扭矩Tin的绝对值期望为45 N·m（15%电机额定扭矩），转速测量编码器转角测量误差的绝对值期望为5×10-6rad（雷尼绍300 mm圆光栅编码器）；以外界扰动扭矩为主的离心机设备，对应外界扰动扭矩TL的绝对值期望为20 N·m，系统内部扰动扭矩Tin的绝对值期望为4.5 N·m（1.5%电机额定扭矩），转速测量编码器转角测量误差的绝对值期望为3×10-5rad（雷尼绍50 mm圆光栅编码器）。

基于此将联轴器扭转刚度设为1×104，3×104，1×105，3×105，1×106，3×106，1×107，3×107，1×108N·m/rad等9个等级进行仿真，并通过调节转速环增益系数Kω改变伺服驱动系统的调速频率，使离心机系统的转速波动量绝对值期望达到最小（单位：rpm）。仿真结果如图3所示，其显示了在两类仿真目标下，随着联轴器扭转刚度的增长，离心机系统转速波动量的对应变化趋势。

依据仿真结果，可以发现在以外界扰动扭矩为主的离心机系统中，系统最小转速波动量随着联轴器扭转刚度的增大逐渐降低，并最终收敛；同时与系统最小转速波动量相对应的伺服驱动系统调速频率随着联轴器扭转刚度的增大逐渐上升，并最终收敛。可以认为，选取扭转刚度较高的联轴器确实有助于降低该运转工况下离心机系统的转速波动量，但由于伺服驱动系统调速频率的设计需要平衡调整扭矩与系统自生扰动扭矩，因此系统对于调速频率的需求存在一个上限值，即对应仿真结果中的收敛点。由此可知，过高的联轴器扭转刚度对于系统转速稳定度并没有优势，反而会增加系统的安装难度。

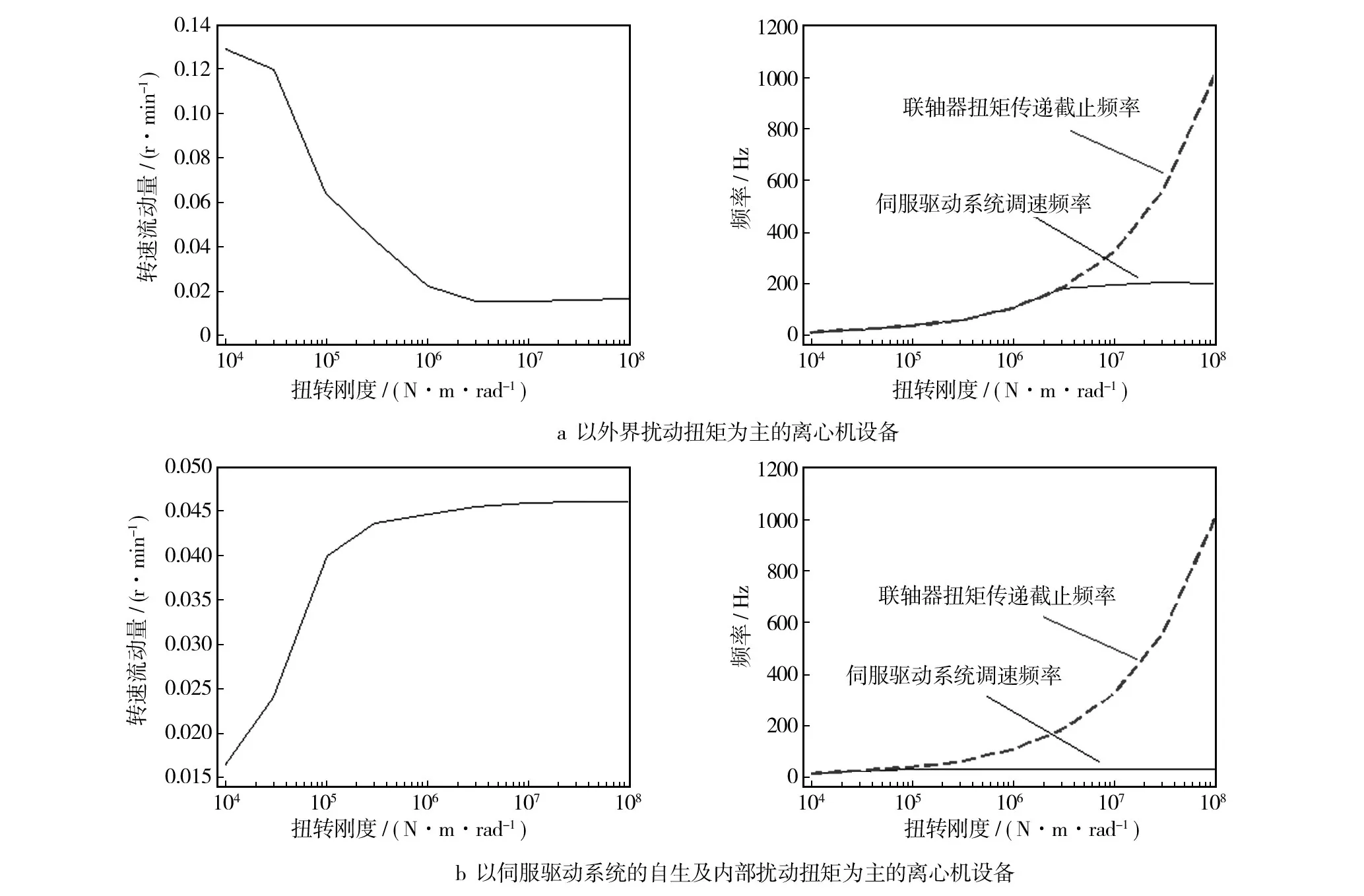
图3 仿真结果Fig.3 The simulation results

在以伺服驱动系统的自生及内部扰动扭矩为主的离心机系统中，系统最小转速波动量随着联轴器扭转刚度的增大逐渐上升并最终收敛，同时与之对应的伺服驱动系统调速频率随着联轴器扭转刚度的增大却基本没有增加。这是由于在这一运转工况下，系统以抑制自生扰动扭矩为首要控制目标，因此对于调速频率的需求较低（在该工况下约为25 Hz，远低于以外界扰动扭矩为主的工况中接近200 Hz的需求），从而限制了系统的动态响应能力。故扰动扭矩（以系统内部扰动扭矩为主）将基本不受伺服驱动系统调整扭矩的影响，并直接通过联轴器作用于系统负载之上，此时扭转刚度更低的联轴器所拥有的更小低通滤波截止频率将有助于消除高频段扰动扭矩对系统转速稳定度的影响。

4 结论

文中基于Matlab/Simulink仿真平台，通过建立包含联轴器刚性及阻尼特征模块的离心机转速伺服控制系统仿真模型，就联轴器扭转刚度对离心机系统转速稳定度的影响进行了仿真分析。基于该模型，能够为离心机系统中联轴器的设计选型工作提供必要依据。

研究表明，联轴器扭转刚度对离心机系统转速稳定度的影响来源于其对离心机系统动稳态调速性能的限制。选用扭转刚度较高的联轴器有助于提升离心机系统的动态性能以及对抗外界扰动扭矩的能力，选用扭转刚度较低的联轴器能够提升系统的稳态性能，并降低系统驱动环节固有扰动扭矩所造成的影响。因此在离心机设计过程中，应根据离心机系统的动稳态性能需求、扰动扭矩组成、以及安装难度等因素选择扭转刚度适中的联轴器作为系统动力传递装置。

不同离心机系统对动稳态调速性能的需求是不同的，因此针对离心机转速稳定度的联轴器设计选型，必须综合考虑离心机系统结构、系统扰动扭矩组成等因素。在确定离心机系统所要求的调速响应频率之后，方可基于联轴器的二阶滤波器特征对其技术指标进行设计，使之具备合适的扭矩传导截止频率。

[1] 熊磊，何懿才，龙祖洪，等.精密离心机不确定度分析与应用[J].误差分析，2003，23（6）：36—37.XIONG Lei，HE Yi-cai，LONG Zu-hong，et al.Uncertainty Analysis and Application of Precise Centrifuge[J].Journal of Error Analysis，2003，23（6）：36—37.

[2] QUANG N P，DITTRICH J A.Vector Control of Three Phase AC Machines：System Development in the Practice[M].New York：Springer，2008.

[3] JAHNS T M，SOONG W L.Pulsating Torque Minimization Techniques for Permanent Magnet AC Motor Drives，A Review[J].IEEE Trans.on Industrial Electronics，1996，43（2）：321—330.

[4] 黄鹏，尹益辉，徐建国.振动复合离心机风阻功率及启动过程分析[J].工程设计与力学环境，2006（3）：38—44.HUANG Peng，YIN Yi-hui，XU Jian-guo.The Analysis on the Wind Resistance Power and the Boot Process of the Vibration Compound Centrifuge[J].Engineering Design and Mechanical Environment，2006（3）：38—44.

[5] 苏芳.柔性联轴器对振动系统动态响应影响的研究[D].上海：复旦大学，2011.SU Fang.The Research on the Flexible Coupling′s Effect on the Dynamic Response of Vibration System[D].Shanghai：Fudan University，2011.

[6] 李珍国.交流电机控制基础[M].北京：化学工业出版社，2009.LI Zhen-guo.AC-Motor Control[M].Beijing：Chemical Industry Press，2009.

[7]马建敏，韩平畴.柔性联轴器刚度非线性对扭转振动的影响[J].振动与冲击，2005，24（4）：6—8.MA Jian-min，HAN Ping-chou.The Nonlinear Stiffness of Flexible Coupling Effect on the Torsional Vibration[J].Journal of Vibration and Shock，2005，24（4）：6—8.

[8]马建敏，杨万东.柔性联轴器非线性阻尼对扭转减振的影响[J].振动与冲击，2006，25（3）：11—13.MA Jian-min，YANG Wan-dong.The Nonlinear Damping of Flexible Coupling Effect on the Torsional Vibration[J].Journal of Vibration and Shock，2006，25（3）：11—13.

[9] 三谷政昭.模拟滤波器设计[M].北京：科学出版社，2014.MITANI M.Analog Filter Design[M].Beijing：Science Press，2014.