一类飞行器动态变化加速度模拟试验原理探索

张东锋，欧峰

（中国工程物理研究院 总体工程研究所，四川 绵阳 621900）

导弹、飞机等飞行器从发射起飞至下降着陆等过 程中都会承受持续加速度载荷，该持续加速度载荷的一类典型地面模拟方法是通过离心机实现的。若该持续载荷从某种典型特征面截取，则称之为稳态加速度模拟试验，模拟过程中飞行器与离心机的相对位置保持不变。如果需要模拟飞行器的连续动态变化，通常需要在离心机上安装常平架进行动态控制，称之为离心机连续动态模拟系统[1]。若加速度变化率大，则称为高动态模拟系统。从设备研发角度而言，模拟时输入角速度或角加速度可以实现某特定点的目标加速度，力学理论上称之为运动学正问题[2—5]，而加速度模拟试验原理研究却属于运动学逆问题范畴。运动学逆问题存在多值性和对初值的依赖性，比正问题复杂得多，目前主要集中在机器人领域，关于多轴运动研究较少。

文中首先针对研发的特殊高动态模拟系统建立三轴高动态加速度模拟系统的数学模型，从运动学正问题出发，探讨试件加速度与模拟系统各主要结构部件的角加速度、角速度及旋转角度之间的关系。通过反解方程，得到所需的角速度、角加速度及旋转角度，最后运用Matlab对双轴运动简例进行仿真分析。

1 数学模型

不同需求的加速度动态模拟系统中，常平架的安装方式也不同。如土工离心机中使用吊斗，在不同加速度载荷下离心机半径会动态改变，但不能人为控制吊斗，属于一种双轴模拟系统。飞行员和飞行器模拟系统通常使用内、中、外框等动量矩框架以及离心机转轴共同构成多轴旋转系统。文中研究一种特殊的离心机动态模拟系统，其常平架某转轴始终与离心机转轴方向相同，模拟系统外观如图1所示。该系统固定了三轴模拟系统的两轴方向，第三方向上试件可以自旋。动态模拟系统数学模型的几何描述与相关坐标系如图2所示。

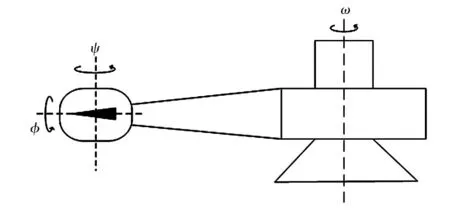
图1 某动态模拟系统Fig.1 Sketch map of simulation system with three-axial variable accelerations

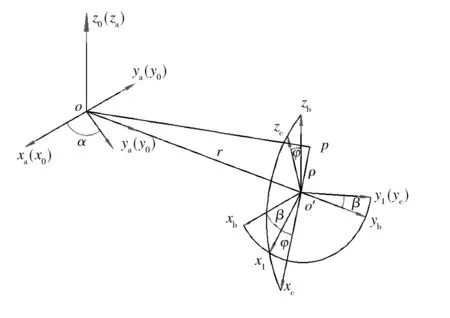
图2 动态模拟系统的数学模型Fig.2 Mathematical model of simulation system with three-axial variable accelerations

2 三轴加速度模型运动方程的建立

2.1 三轴加速度模型及相关坐标系

三轴加速度模型如图2所示，其中S0为惯性坐标系，Sa为与离心机固连的坐标系，S0，Sa的原点为o点。在离心机旋转研究中，通常以Sa坐标系代替S0坐标系进行惯性系研究，Sb为吊篮处与离心机固连的坐标系，它与Sa相差一臂长，记为矢量r。实际可以认为是同一坐标系，Sc是与常平架固连的坐标系，通常与飞行器固连，为本体坐标系，Sc与Sb的原点为常平架中心o′点。Sc是通过Sb先绕z轴旋转β，再绕y轴旋转φ实现的，旋转顺序表示为[6—9]：

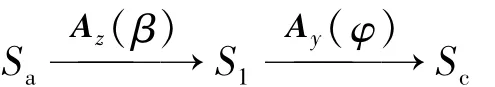
式中：Az（β）,Ay（φ） 为旋转矩阵；S1为中间过渡坐标。从Sa到Sc的转换矩阵Aca为：

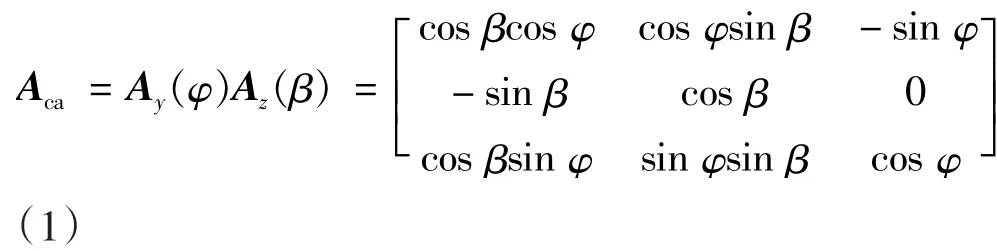
记从Sc到Sa的转换矩阵为Aac。

2.2 相对角速度、相对角加速度

相对于本体坐标系的角速度矢量可以表示为[10—14]：

相对角加速度Sc坐标系下的列阵形式为：

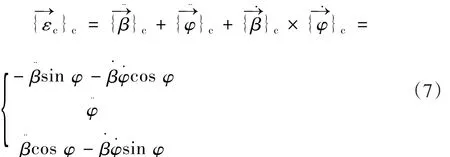
2.3 三轴加速度模型的建立

惯性坐标系下的速度及加速度矢量为：

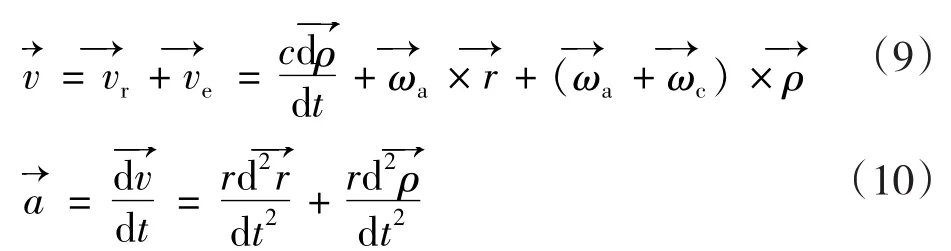
因为Sa坐标平移加速度式（10）整理为公式（11）：

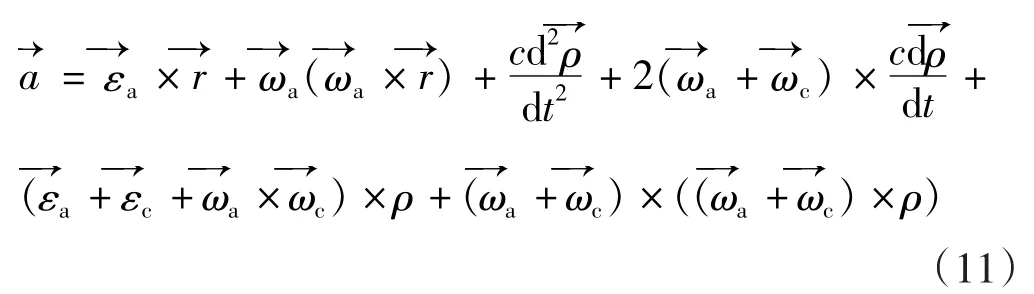
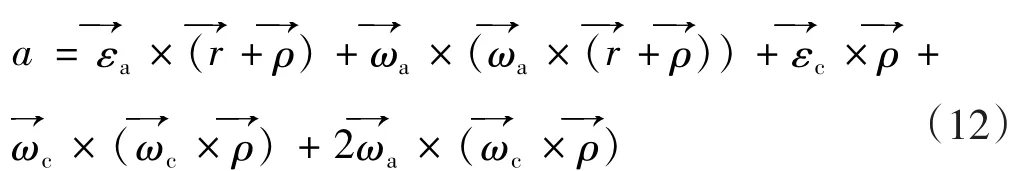
离心机旋转的角速度在Sa坐标系下的矢径表示为｛为其在Sa坐标系下的叉乘矩阵，为其在Sc坐标系下的叉乘矩阵，角加速度也同样表示，记为｛Sc坐标系原点点在Sa坐标系下的矢径表示为变 矢 量为了简化公式，将 Sa坐标系下的分量记为的位置矢量在Sa坐标系下的列式为：，则式（8）表示

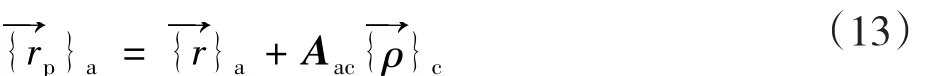
式（12）的绝对加速度在Sa坐标系下的列式为：

式（14）表示的加速度在x，y，z三个方向都存在偏移，试验中最常见的情况为z向、x向偏移设为0，仅仅

存在自转轴y向的偏移量，那么：

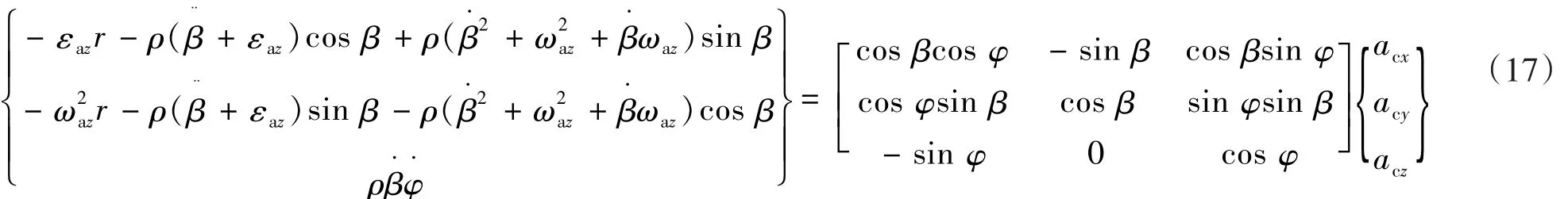
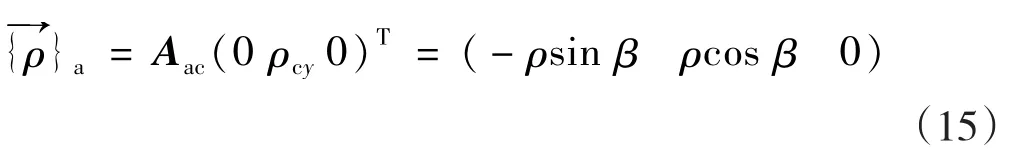
则（14）式改为：

通常试验中Sc坐标系下的绝对加速度已知，则Sc坐标系和Sa坐标系两坐标系下的绝对加速度转换公式为：

式（17）为三轴旋转时需要求解的微分方程，复杂问题需要求解该方程。为了算例简单，不考虑偏移量，即变矢量，同时不考虑重力加速度的影响，则φ=0。式（17）简化为：

简化公式为求解每时刻的圆周运动和试件转角。为了避免无解和多值波动，下面算例中将式（18）的角加速度作线性化处理，将方程转换为代数方程，计算时先联立求解角速度和角加速度，最后求解试件的旋转角度。

3 算例

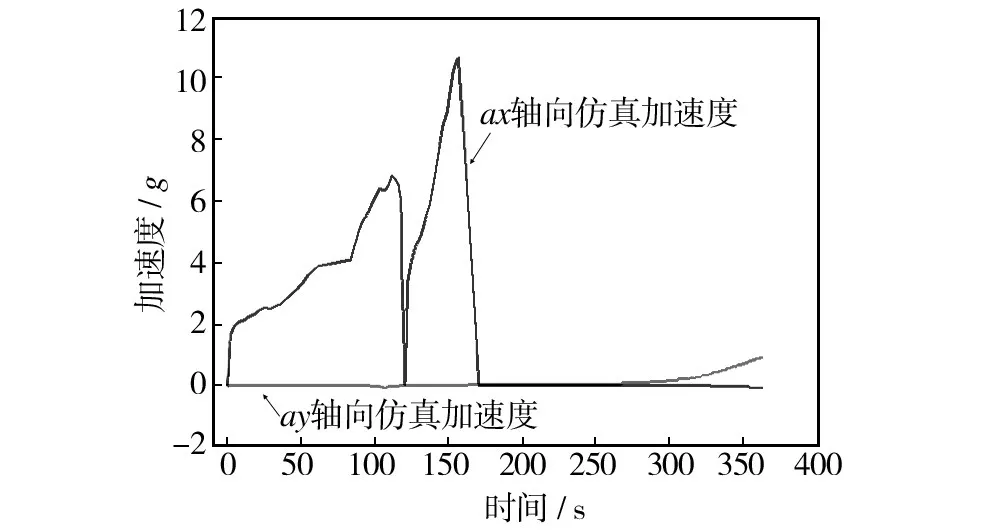
图3 试件轴向和横向目标加速度变化曲线Fig.3 Axial and transverse project accelerations

文中算例同时具有轴向和法向加速度，算例中机臂长r=3.5 m，轴向及法向目标加速度同时随时间的变化曲线如图3所示。试验时需要同时实现轴向和法向加速度动态变化，并且在整个试验过程中反映轴向和法向加速度剧烈的动态变化。

通过Matlab求解[15]处理后的方程（18），离心机旋转角速度和试件旋转角度如图4和图5所示。图5说明当轴向值趋近0时，横向目标的微小变化需要通过较大转角变化来实现。通过计算获得的离心机角速度和试件转角模拟仿真轴向加速度和横向加速度与目标加速度比较如图6所示。从图6a中可见，当加速度经剧烈变化到突然长时间变为0时，由于离心机的角加速度始终处于趋近于0的状态，横向模拟值与目标横向加速度存在0.07g的差值。从整体上以及图6b所示的横向加速度可知，能够很好地模拟轴向和横向的动态变化加速度。

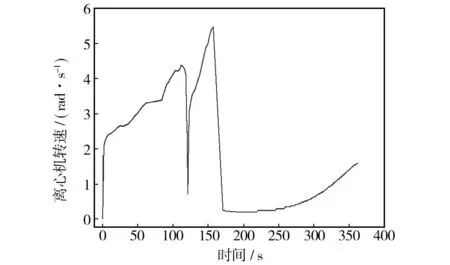
图4 离心机角速度随时间变化曲线Fig.4 Angular velocity of centrifuge

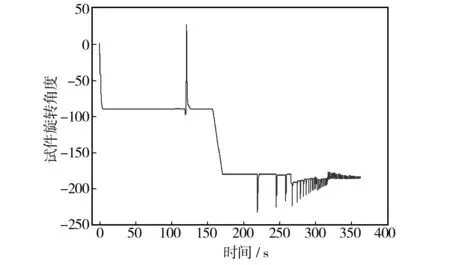
图5 试件旋转角度随时间变化曲线Fig.5 The changing curve of rotation angle of product over time

4 结语

图6 试件模拟值与目标加速度比较Fig.6 Comparison of transverse simulated value and objective acceleration

文中通过建立三轴动态变化加速度模拟系统的数学模型，从运动学正问题出发，建立了试件目标加速度与模拟系统各驱动结构的角加速度、角速度之间的关系，通过Matlab反解方程，并对方程进行线性化处理，减小初值的影响和多值性的影响，得到所需的角速度和试件旋转角度，最后对双轴运动简例进行仿真分析，仿真结果表明反解方程进行动态加速度模拟试验是可行的。

[1]贾普照.稳态加速度试验模拟设备——离心机理论与设计[M].北京：国防工业出版社，2013.JIA Pu-zhao.The Design of a Steady State Acceleration Simulation Test Equipment－Centrifuge[M].Beijing：National Defence Industry Press，2013.

[2] 由俊生，由勇，许叙遥，等.歼击机飞行员三轴加速度过载建模与仿真研究[J].系统仿真学报，2006，18（S2）：28—30.YOU Jun-sheng，YOU Yong，XU Xu-yao，et al.Research for Modeling and Simulation of Pilot Three Shaft Acceleration[J].Journal of System Simulation，2006，18（S2）：28—30.

[3] 马杰，姚郁.一种新型动态飞行过载模拟器及其运动学分析[J].系统仿真学报，2009，21（S2）：112—114.MA Jie，YAO Yu.Kinematics Analysis of a New Flight Acceleration simulator[J].Journal of System Simulation，2009，21（S2）：112—114.

[4] 马智周.三轴运动模拟转台的运动学和动力学[J].航空精密机械工程，1988（3/4）：28—34，9—13.MA Zhi-zhou.Kinematics and Dynamics of Three-axial Motion Simulated Turnable[J].Aviation Precision Manufacturing Technology，1988（3/4）：28—34，9—13.

[5] 潘文俊，王立新.持续载荷飞行模拟器过载模拟新原理[J].航空学报，2010，31（11）：2159—2164.PAN Wen-jun，WANG Li-xin.Principles of G-load Simulation for a Novel Sustained-G Flight Simulator[J].Acta Aeronautica et Astronautica Sinica，2010，31（11）：2159—2164.

[6] 赵育善，师鹏.航天器飞行动力学建模理论与方法[M].北京：北京航空航天大学出版社，2012.ZHAO Yu-shan，SHI Peng.The Modeling and Method of the Flight Dynamics on Space Shuttle[M].Beijing：Beijing University of Aeronautics and Astronautics Press，2012.

[7]肖业伦.航空航天器运动的建模——飞行动力学的理论基础[M].北京：北京航空航天大学出版社，2003.XIAO Ye-lun.The Modeling of Aerospace Vehicle－The theory of The Flight Dynamics[M].Beijing：Beijing University of Aeronautics and Astronautics Press，2003.

[8] 袁惠群.转子动力学基础[M].北京：冶金工业出版社，2013.YUAN Hui-qun.The Foundation of Rotor Dynamics[M].Beijing：Metallurgy Industry Press，2013.

[9] 徐明友，丁松滨.飞行动力学[M].北京：科学出版社，2003.XU Ming-you，DING Song-bin.The Dynamics of Flight[M].Beijing：Science Press，2003.

[10]贾书惠.刚体绕定点运动中的角速度和角加速度[J].力学与实践，1991，13（6）：50—53.JIA Shu-hui.The Angular Velocity and Acceleration for Rotation of Rigid Body with one Fixed Point[J].Mechanics in Engineering，1991，13（6）：50—53.

[11]李向荣，蔡屹立，潘红萍.刚体绕定点运动的角加速度合成公式[J].力学与实践，1989，11（5）：68—69.LI Xiang-rong，CAI Yi-li，PAN Hong-ping.The Angular Acceleration Compound Formula of Rigid Body Around a Fixed Point Motion[J].Mechanics in Engineering，1989，11（5）：68—69.

[12]陈勇.刚体在复合运动中角速度、角加速度合成定理[J].贵州师范大学学报（自然科学版），2000，18（4）：89—90.CHEN Yong.The Angular Velocity and Acceleration Composing Theorem of rigid body in compound motion[J].Journal of Guizhou Normal University（Natural Science Edition），2000，18（4）：89—90.

[13]张献图.四重转动参考系与质点的运动[J].河南教育学院学报（自然科学版），1997，6（1）：33—36.ZHANG Xian-tu.The Motion of Four Rotation Reference Frame and Material Point[J].Journal of Henan Institute of Education（Natural Science Edition），1997，6（1）：33—36.

[14]CHEN Wan-chun，XIAO Ye-lun.Relationship for Motion When Described in Any Two Rotational Reference Frames[J].Chinese Journal of Aeronautics，1999，12（4）：40—43.

[15]敖文刚，杜力，黄勇刚，等.基于MATLAB的运动学、动力学过程分析与模拟[M].北京：科学出版社，2013.AO Wen-gang，DU Li，HUANG Yong-gang，et al.Application of Matlab to Process Analysis and Simulation of Kinematics and Dynamics[M].Beijing：Science Press，2013.