600g-t 土工离心机吊篮力学分析与强度设计

杨玉明，刘远东，王沪毅

（中国工程物理研究院 总体工程研究所，四川 绵阳 621900）

土工离心机是用来模拟重力场，进行土工建筑物缩模试验研究的重要设备。土工离心模型试验是将1/n的模型置于离心机中，在n倍g离心加速度的空间进行试验。由于惯性力与重力绝对等效，且高加速度不会改变工程材料的性质，从而使模型和原型的应力、应变相等，变形相似，塑性区发展和破坏过程相似，以获取原型变形破坏机理和破坏过程的物理模拟试验技术[1—2]。土工离心机由传动系统、转臂系统、吊篮几大部件构成。吊篮是试验件的承载结构，试验件放置于模型箱中，模型箱安装在吊篮底部平台上，吊篮上端通过销轴连接于转臂的末端。在工作状态下，吊篮自身所受的重力产生离心力，离心机转速越高，离心力越大。模型箱及试验件也将产生很大的离心力，该离心力作用于吊篮平台上，因此，吊篮是关键的承力系统。这要求吊篮是高比强度、高比刚度的结构体系，在其强度设计和力学分析中，通常需对吊篮进行优化设计，文献[3—6]针对多个型号的离心机吊篮结构整体开展了优化设计，得到了满意的结果。

文中的土工离心机的容量为600g-t，有效旋转半径为5 m，有效旋转半径处（模型试验中心）的最大加速度达到200g，最大转速达到19.8 r/s，是目前国内较大的土工离心机。在对离心机吊篮初始设计方案进行力学分析的基础上，对吊篮开展了优化设计。因吊篮由多个部件构成，对吊篮作整体优化分析约束条件太多，不易收敛到满意的结果。不同于文献[3—6]，文中对结构的各个部件开展优化分析，在对吊篮结构作整体计算。通过优化设计，得到了满足强度要求的吊篮结构参数。

1 计算方法

1.1 接触算法

吊篮部件之间的连接为接触配合连接，吊耳与上端的向心关节轴承和下端的销轴均为接触配合，底部平台与销轴之间也为接触配合，在结构的力学响应分析中需要采用接触算法。

接触问题属于高度复杂的非线性问题，表现在接触的区域随时间不断变化，约束条件非常复杂，接触界面的摩擦条件也十分复杂。分析复杂的接触非线性力学问题，通常采用Lagrange乘子法和罚方法[7—11]。

Lagrange乘子法和罚方法是把约束条件乘以Lagrange乘子λ或罚参数α，并引入离散结构系统的变分公式，从而处理复杂的约束条件。Lagrange乘子作为独立的变量，即在平衡方程中增加了场变量，从而导致计算量增加。罚函数法是引入罚参数以消去平衡方程中的某一场变量，其困难在于罚参数的选择，会出现收敛性问题。

在接触分析中，通过位移约束来阻止网格的交叠，而且还要控制接触面网格的相互滑动。接触模型把可能发生相互接触的体（面或线）分为接触体和目标体，在增量方法的某步迭代中，当接触体上的节点k进入目标体的目标单元内时，若发生交叠，则通过返回节点k到目标单元的边界上。当接触体上的节点k是在滑动接触中，则位移约束应仅施加法向约束。约束方程为：

对于Lagrange乘子法，增量平衡方程为：

将式（1）的约束方程引入罚方法的平衡方程，其增量迭代方程为：

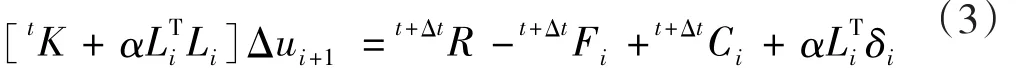
ANSYS软件具有较强的接触分析功能，支持点-点接触、点-线接触、点-面接触、点-体接触、面-面接触、面-体接触，通过调节法向接触刚度、初始接触关闭条件、切向罚刚度等实常数，可以提高收敛速度以及计算精度。文中采用Ansys软件增进的拉格朗日方法——Augmented Lagrangian Method来分析结构的接触非线性。该方法可寻找到精确的拉格朗日乘子，对罚函数进行修正迭代[12]。

1.2 优化分析方法

优化设计包括设计变量、目标函数和约束条件三个要素。目标函数表述为：

式中：x1，x2，…，xn为设计变量。

约束条件为：

或：

G（x）是不等式约束，H（x）是等式约束。目标函数是优化所要求最优设计性能，一般以结构的某要素作为目标函数，如质量最小或体积最小等。文中以Ansys软件来作结构的优化分析。

2 吊篮有限元分析及优化设计

2.1 吊篮结构

离心机吊篮由2个吊耳、底部平台以及销轴构成，如图1所示。其中，底部平台是由4根梁、加强筋板、底板和顶板焊接在一起的整体，底部平台的顶板上放置试验用模型箱。销轴用于连接底部平台与吊耳，吊篮的上端通过向心关节轴承与转臂系统的拉力带叉耳相连接。吊耳与销轴采用高强度钢34CrNi3Mo，底部平台采用Q690。离心机运转时，离心机主轴带动转臂旋转，转臂带动吊篮旋转，吊篮及模型箱受到离心力的作用。

图1 吊篮结构Fig.1 Structure of nacelle

2.2 有限元分析结果

吊耳上端孔与向心关节轴承为接触配合，连接吊耳与底部平台的销轴与吊耳下端孔和梁的孔也为接触配合，在这些接触配合部位建立面-面接触单元。由于结构和载荷的对称性，取1/4吊篮来建模。有限元模型如图2所示。在对称面施加面对称约束，在吊耳上端向心关节轴承内的销轴两端施加固支约束。

吊篮受到的角速度为19.8 rad/s，模型箱及试验件产生600g-t离心力，以压力的形式作用于吊篮底部平台上。在这两个载荷的作用下，吊篮的力学响应如图3所示。图3表明，吊耳上端孔、吊耳下端孔边缘、梁的孔边缘以及销轴退刀槽边缘存在应力集中，其中，吊耳的最大应力达到了772.9 MPa，销轴的最大等效应力达到1252.6 MPa，超过了材料的屈服强度。吊篮不满足强度要求。

图2 吊篮有限元模型Fig.2 FEM model of nacelle

2.3 吊篮结构优化设计

2.3.1 吊篮结构优化设计思路

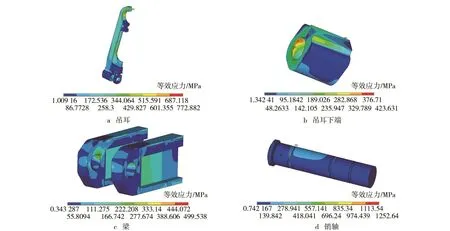
图3初始结构的等效应力Fig.3 Nephogram of von Mises stress of original structure

图3 的结果表明，吊耳上端孔以及下端销轴的应力较大。在离心机工作状态下，结构自身所受的重力产生离心力，质量越大，离心力越大。为减小离心机工作状态下吊篮受到的离心力，吊篮应设计为质量轻而刚度大的结构，据此对吊篮作了优化分析。因吊耳和销轴是关键承力件，吊耳上端是关键承力部位，对吊耳上端以及销轴进行加强，减轻吊篮底部平台的质量以降低吊篮自身的重力。对吊耳、销轴、底部平台以质量最小为目标，以应力满足强度要求为约束条件进行了优化。优化后吊篮结构作了以下改进：

1）增加吊耳上端孔凸台轴向长度及厚度，增加吊耳上端外缘直径；

2）将销轴由实心轴改为空心轴，并增加销轴外径，达到提高销轴抗弯截面模量、减轻销轴质量的目的；

3）增加加强筋板减重孔直径，梁的中间筋板开减重孔，底板厚度减薄。

图4为优化前、后的结构。

2.3.2 优化后吊篮结构力学响应

图5为优化后吊篮结构的等效应力云图。图5表明，优化后吊篮各部件的应力分布规律与优化前基本一致，但各部件的最大等效应力值较优化前下降很多。优化前、后吊篮结构各部件的最大等效应力见表1。可以看出，优化后吊耳的最大等效应力较优化前下降了48%，销轴的最大等效应力较优化前下降了59%，底部平台的最大等效应力较优化前下降了39%。优化后的吊篮结构的强度满足设计指标要求。

图4 优化前后吊篮部件结构Fig.4 Comparison of part structure of nacelle before and after optimization

图5 优化结构的等效应力Fig.5 Von Mises stress of optimizational structure

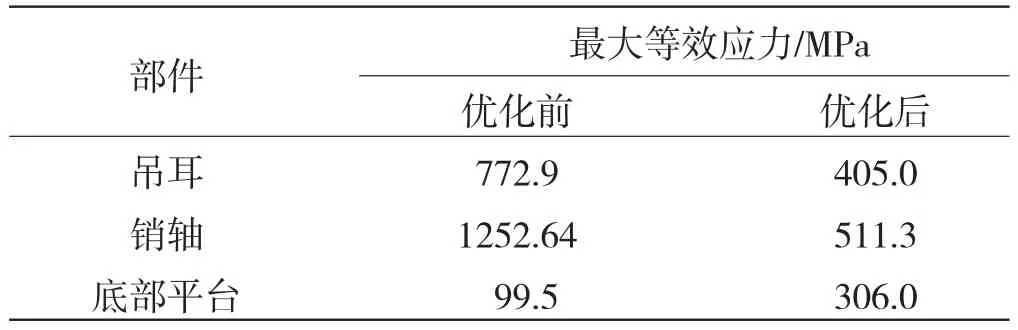
表1 优化前后吊篮的最大等效应力Table 1 Maximum von Mises stress of optimizational structure

3 结论

文中对吊篮结构的初始设计方案进行了有限元接触分析，在此基础上开展了吊篮各部件的优化分析。优化后吊篮结构的力学分析结果表明，吊篮各部件的应力大幅度下降，尤其是吊耳和销轴这两个关键承力部件应力分别下降了48%和59%。通过优化后得到了满足强度要求的吊篮结构参数。

[1] 白冰，周健.土工离心模型试验技术的一些进展[J].西部探矿工程，2000（4）：8—11.BAI Bing，ZHOU Jian.Progress Report of the Soil Centrifugal Model Test[J].West-China Exploration Engineering，2000（4）：8—11.

[2] 刑建营，刑义川，梁建辉.土工离心模型试验研究的进展与思考[J].水利与建筑工程学报，2005，3（1）：27—30.XING Jian-ying，XING Yi-chuan，LIANG Jian-hui.Review of the Soil Centrifugal Model Test[J].Journal of Water Resources and Architectural Engineering，2005.3（1）：27—30.

[3] 王东升，刘青林，钟继根，等.某型号离心机吊篮拓扑优化设计[J].航天器环境工程，2009，26（3）：254—258.WANG Dong-sheng，LIU Qing-lin，ZHONG Ji-gen，et al.Topological Optimization of the Nacelle on Centrifuge[J].Spacecraft Environment Engineering，2009，26（3）：254—258.

[4] 陈磊，洪建中，杨永生，等.相对变形约束下某离心机吊篮拓扑优化设计[J]. 航天器环境工程，2012，29（1）：100—103.CHEN Lei，HONG Jian-zhong，YANG Yong-sheng，et al.Topological Optimization of the Nacelle on Centrifuge Via Relative Deformation Constraint[J].Spacecraft Environment Engineering，2012，29（1）：100—103.

[5] 冉光斌，罗昭宇，刘小刚，等.土工离心机吊篮的设计及优化方法[J].机械设计，2009，26（11）：68—70.RAN Guang-bin，LUO Zhao-yu，LIU Xiao-gang.Design and Optimization Methods of the Nacelle on Soil Centrifuge[J].Journal of Machine Design，2009，26（11）：68—70.

[6] 冉光斌，洪建中，刘小刚.巨型多功能土工离心机吊篮的设计[J].机械设计，2011，28（10）：33—36.RAN Guang-bin，HONG Jian-zhong，LIU Xiao-gang.Design of the Nacelle on Giant and Multifunctional Soil Centrifuge[J].Journal of Machine Design，2011，28（10）：33—36.

[7]MOTTERSHEAD J E，PASCOE S K，ENGLISH R G.A General Finite Element Approach for Contact Stress Analysis[J].Int J Numer Meth Eng，1992，33：765—779.

[8] REDDY J N.Penalty-finite-element Analysis of 3-D Navier-Stokes Equations[J].Compu Meth Appli Mech Engng，1982，35：87—106.

[9] KIKUCH N.A Smoothing Technique for Reduced Integration Penalty Methods in Contact Problems[J].Int J Numer Mech Engng，1982，18：343—350.

[10]KANTO V，YAGAWA G.A Dynamic Contact Buckling Analysis by the Penalty Finite Element Method[J].Int J Numer Mech Engng，1990，29：755—74.

[11]REDDY M P，REDDY J N，AKAY H U.Penalty Finite Element Analysis of Incompressible Flows Using Element by Element Solution Algorithms[J].Computer Methods in Applied Mechanics and Engineering，1992，100：109—205.

[12]张洪才，何波.有限元分析—ANSYS13.0从入门到实战[M].北京：机械工业出版社，2011.ZHANG Hong-cai，HE Bo.FEM Analysis for ANSYS13.0[M].Beijing：China Machine Press，2011.