钢轨无损检测中的超声导波技术

周建民，徐清瑶，李 鹏，万 琪，廖晓苏

(华东交通大学机电工程学院，江西南昌 330013)

0 引言

钢轨在使用过程中，由于自然因素以及列车载荷的作用，致使其表面和内部易产生各类损伤和缺陷，严重时甚至会造成钢轨断裂、列车脱轨等重大事故［1］。因此，开展钢轨无损检测技术的研究具有重要的意义。

超声波检测是钢轨无损检测的重要手段之一。目前，常规超声波检测方法有脉冲反射法、穿透法和共振法等［2］。这些方法在技术方面比较成熟，但其检测过程采用逐点扫描方式，检测速度慢，已较难满足现阶段我国铁路轨道高速发展的需求。与常规超声波检测方法相比，新型的超声导波技术具有沿传播路径衰减小、传播距离远、检测速度快等优点，已被广泛应用于管道等大型构件的无损检测中［3］，并且该技术在钢轨大范围缺陷的完整性检测上具有良好的应用前景。因此，钢轨超声导波检测技术已成为近年来国内外无损检测领域研究的热点之一。

1 导波检测原理

机械振动在弹性介质中的波称为弹性波(即声波)，而频率大于20 kHz的声波则称为超声波。当超声波被局限在具有边界的介质(如平板、管道等)内传播时，超声波将会在边界处不断地反射，从而沿着介质的方向传播形成超声导波［4－5］。产生超声导波的这种具有边界的介质称为波导，轨头、轨腰和轨底是钢轨中三种典型的波导。由于这些波导的结构不同，在其中传播的导波频率和速度也相应发生变化。

用超声导波对钢轨进行无损检测时，可以通过信号发生装置产生激励信号，经功率放大器放大后由导波传感器在钢轨的一端激发超声导波。如果导波沿着没有损伤的轨头、轨腰和轨底传播，那么导波的群速度和相速度就基本保持一致。如果导波在传播过程中遇到界面不连续处(如轨底腐蚀)，则可能发生反射、散射和模式转换，这样便会产生携带局部缺陷特征的回波［6］，如图1所示。通过对回波信号进行分析就可以确定缺陷的位置，回波幅值还能够用于钢轨损伤程度的评定。

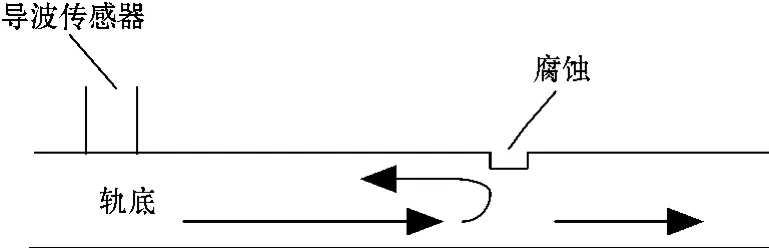
图1 超声导波检测原理(以腐蚀为例)

2 导波的频散及多模态特性

相对于体波(常见的超声波)，钢轨中超声导波的显著特点就是具有频散特性。导波在钢轨轨头、轨腰和轨底中传播时，由于受波导截面形状和尺寸的影响，使得在钢轨中传播的超声波速度依赖于波的频率，从而导致超声波的几何弥散，即导波的相速度随频率的不同而发生变化，这种现象就称为钢轨中超声导波的频散现象［7］。频散对超声导波的传播有很大影响，主要表现为导波信号在传播一定距离后时域波包的宽度会拉长，幅度明显减小，这不仅降低了检测的灵敏度，而且会给后续信号处理带来很大的困难。因此，应尽量避免将频散严重的导波模态用于钢轨的无损检测。

多模态是钢轨中超声导波的另一重要特性。波导结构一般在某一频率下至少存在两个或两个以上的导波模态，它们在波导中以不同的群速度传播。钢轨中的超声导波存在很多种不同的模态，多种模态叠加在一起并分别以不同的速度传播可能会使数据信号解析变得困难［8］。因此，需要合理选取合适的模态来检测钢轨不同部位、不同类型的典型缺陷。

3 钢轨中超声导波传播特性的数值计算

超声导波的传播特性(频散、波结构等)在很大程度上影响着其检测效果［9］。因此，应用导波技术对钢轨进行无损检测时，需要根据导波的传播特性来选择合适的导波模态和频率范围。规则截面波导(如板、管)中导波传播特性的数值计算方法已经很成熟［10－12］，但由于钢轨是异型截面波导，一般的商用软件无法完成其传播特性的数值计算，因此，钢轨中超声导波传播特性的数值计算一直是导波检测研究的热点。

国外很多学者应用半解析有限元(Semi－analy－tical finite element，SAFE)法对钢轨中超声导波的传播特性进行了相关研究。该方法由Taweel等［13］提出，可用于求解任意截面波导中超声导波的传播特性。将该方法应用于钢轨时，只需对钢轨横截面进行离散，沿波传播方向上的位移用谐波指数函数eikx(x为钢轨长度，k为导波的波数)来描述，从总体运动方程特征值系统中解得特征值ki(即，第i个共振模式的波数)后，便可获得频散关系。

Hayashi等［15］采用半解析有限元法计算日制JIS50型钢轨中超声导波的频散曲线，得到了导波在0～100 kHz范围内的相速度、群速度频散曲线，分别如图2和图3所示(其中，横坐标均为激励频率，纵坐标分别为钢轨中导波随激励频率变化的相速度和群速度)。从图中可以看出，钢轨在该频率范围内存在众多传播模式，有些模式的导波频散曲线在一定的频率范围内较为平缓，展现了较好的传播特性，可用于检测。为了验证数值计算结果，Hayashi等分别对轨头踏面和轨头侧面进行导波检测实验，实验得到的相速度、群速度频散曲线与理论得到的结果非常吻合。

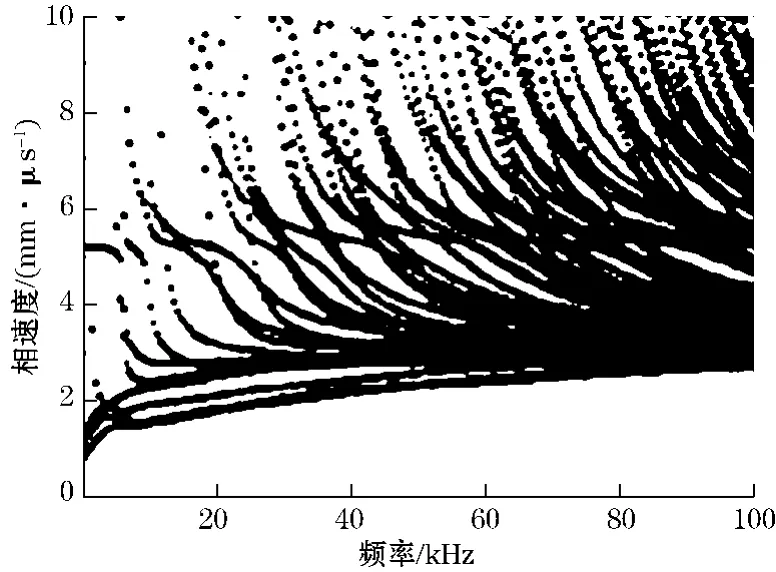
图2 钢轨相速度频散曲线

图3 钢轨群速度频散曲线

同样采用半解析有限元法对钢轨中超声导波的传播特性进行 数 值 计 算 的 还 有 Coccia［16］、Bartoli［17］、Loveday［18－19］、Lee［20］、Hesse［21－22］、卢超［23－24］以及常俊杰［25］等人，Hayashi［26］还结合半解析有限元法开发了一款用于计算钢轨中超声导波频散曲线的软件Rail Dispersion。

除了半解析有限元法，一些学者也采用其他方法来解决钢轨中导波传播特性的数值计算问题。Sanderson等［27］根据固有频率分析可以提供任意频率下结构所有传播模式的位移模态，采用三维固有频率分析方法求出了英制BS113A型钢轨在0～60 kHz范围内的频散曲线。国内何存富等［28］根据结构振动解与波动解的互化原理，采用振动模态分析方法提取出钢轨中导波的相速度和群速度频散曲线，并由钢轨振动分析中获得的变形信息求解出导波的波结构。

以上研究进展有利地推动了钢轨超声导波检测技术的发展，计算出的导波传播特性能为钢轨检测过程中激励频率及导波模态的选择提供依据。

4 激励频率及导波模态的选择

通过对钢轨中超声导波传播特性的数值计算表明，钢轨中存在很多不同种类的导波模态，且随着频率增大钢轨中的导波模态也会增多，因此，在用导波技术对钢轨进行无损检测时应选取合适的激励频率及导波模态。

Gharaibeh等［29］通过ABAQUS建立三维有限元模型进行数值模拟，得到了英制BS113A型钢轨中超声导波的8种模态，如图4所示。对这些模态进行分析，发现F3、T2、F2模态的导波能量都分别集中于单一部位(轨头、轨腰或轨底)，且在70 kHz时这三种模态的导波相速度基本一致。因此，分别选用70 kHz时F3、T2、F2模态的导波对钢轨缺陷进行检测，结果成功检测出离激励点9 m远处2 mm深的轨头横向缺陷和8 m远处5 mm深的轨底横向缺陷，从而验证了激励频率及导波模态选择的正确性。

Hayashi等［30］指出可将钢轨轨底主要的导波模态分为纵向振动模态、垂直振动模态和横向振动模态，纵向振动模态的导波群速度频散曲线总体上很杂乱且无规律，不适合用于检测，而横向振动模态和垂直振动模态的导波在60～200 kHz频率范围内群速度频散曲线较为平缓，可用于检测。

Lee等［21］指出对钢轨轨头剥离不敏感，而对轨头剥离下方的横向裂纹敏感的频率和模态能用于检测轨头剥离下方的横向裂纹，并得出结论:低频导波可以更好地检测位于钢轨轨头的横向裂纹，且能最大限度地减小剥离带来的影响。

图4 钢轨不同部位的导波模态

Rose等［31］认为适合钢轨检测的频率范围为40～80 kHz，并用电磁超声传感器激励60 kHz的导波进行实验验证。实验表明，该方法可以有效地检测钢轨的横向裂纹，但信噪比较低。

以上研究成果表明，选择激励频率和导波模态时，应保证在所选频率范围内所选模态的导波传播能力强，对缺陷具有较高的灵敏度，同时保证该导波的频散曲线较为平缓，以避开频散严重的检测频带，并且尽可能选择较低的激励频率，以减少钢轨中超声导波模态的数量。

5 导波信号处理方法

应用超声导波对钢轨进行检测时，对于给定的激励频率至少会包含2种模态，并且随着频率的增大模态还会增多，只有通过信号处理方法来区分接收信号的不同模态才能获得导波检测所需的模态。此外，实验获得的检测信号还可能受到实验环境引入的噪声等因素的干扰，这些干扰会影响甚至淹没检测中的有用信号，因此，需要用信号处理方法来增强目标信号［32］。

目前，常用的信号处理方法主要有时域分析、频域分析、时频分析以及小波变换等。由于钢轨中的导波信号同时受时间和频率的限制，具有典型的非平稳随机信号特征，若用单一的时域方法或频域方法则难以达到良好的处理效果，而时频分析是瞬时频谱分析，因此，用时频分析方法处理可以获得更丰富、更准确的信息。

Scale等［33］采用基于小波变换的时频分析方法来表征钢轨中具有多模态及频散特征的导波的传播。对长为4.6 m的美制115－lb AREMA型钢轨进行导波检测实验后，通过时频分析方法识别出了1～7 kHz范围内的3种纵向振动模态、一种横向振动模态以及一种垂直振动模态的导波，并采用Gabor小波变换从检测信号的小波尺度图中提取出了导波的群速度频散曲线和衰减系数曲线。同样采用时频分析方法对钢轨中导波检测信号处理的还有 McNamara［34］、Scalea［35］以及 Bartolia［36］等人。

针对超声导波检测时检测灵敏度和分辨率受钢轨中频散波模态影响较大的问题，Kappatos等［37］提出了一种基于离散小波变换的信号处理方法，并通过添加信噪比为－20～20 dB的频散波形来对这种信号处理方法进行评估，结果表明，该方法能在很大程度上减少频散波带来的影响。

6 导波技术在钢轨无损检测中的工程应用

目前，国外已有一些研究机构研制出了钢轨导波检测设备［38－42］，并将其应用于实际线路的钢轨无损检测。Gurvich等［38］研制了型号为AKR1224的便携式低频超声导波检测仪，如图5所示。该仪器将由12个超声波传感器组成的无线阵列式低频导波检测探头作为其发射和接收单元，并采用脉冲回波法进行检测，无需扫描整个钢轨表面就能快速寻找并定位钢轨中一定距离的缺陷，且能分别对轨头、轨腰和轨底缺陷进行检测。此外，该导波检测仪还内置存储器，用于存放测量结果。大量的现场测试表明，该导波检测仪最长检测距离为30 m，缺陷定位精度能达到0.1 m，且钢轨不同部位的缺陷检测不会相互干扰，检测性能良好。

图5 便携式低频超声导波检测仪

Wilcox等［39］研制了主要用于检测钢轨垂直裂纹和铝热焊缝缺陷的G－Scan钢轨超声导波检测装置，该装置通过一个机械/气动控制系统将传感器阵列干耦合到钢轨上来进行检测，且能控制检测模式和传播方向，满足铁路轨道快速检测的技术指标。

Scalea等［40］研制了基于超声导波的非接触式轨检车，该设备采用激光激励超声导波，并用空气耦合式换能器来接收，能快速检测出水平裂缝下的垂直裂纹。此外，该设备还通过离散小波变换来提高非接触检测的信噪比。

由以上研究成果得知，超声导波技术应用于钢轨时检测速度快且能保证灵敏度，检测性能良好，满足现代铁路轨道高速发展的需求。

7 结束语

超声导波技术作为一种新型的无损检测技术，检测速度快，可以避免逐点检测的费时和高成本，在钢轨的长距离检测中有着明显的优势。目前，钢轨超声导波检测技术在以下几个方面仍有待进一步研究。

(1)近年来国内外多采用半解析有限元法来求解钢轨中超声导波的频散曲线，探索新的频散曲线求解方法对于激励频率及导波模态的选择将会更有帮助。

(2)导波传播过程中存在很多种不同的模态，不排除其他模态的导波对钢轨无损检测会有更佳的效果。此外，还可以选择不同的导波模态对钢轨同一部位缺陷进行检测，通过特定数据融合方法，或许能更为全面地反映实际缺陷的特征。

(3)钢轨缺陷有很多种不同的类型，而目前钢轨超声导波检测技术在检测信号智能分析方面还鲜有文献报道，因此，很有必要选择合适的信号处理方法对检测信号进行准确的特征提取并实现检测信号类型的智能识别。

［1］任远，张友鹏，史宏章，等.基于LabVIEW的超声导波断轨检测系统的设计.铁道运营技术，2010，16(2):16－19.

［2］何学科.钢轨探伤.北京:中国铁道出版社，2009:34－35.

［3］王军阵，王建斌，张轩硕.基于ARM和Linux的超声导波管道检测系统.仪表技术与传感器，2011(4):51－52.

［4］ROSE J L.Ultrasonic waves in solid media.Cambridge，England:Cambridge University Press，1999:82 －92.

［5］丁辉.计算超声学—声场分析及应用.北京:科学出版社，2010:102－132.

［6］徐柳娟，王秋萍.导波技术在管道损伤检测中的应用研究评述.人民黄河，2013，35(3):124 －126.

［7］金建华，金纪东.基于磁致伸缩效应的管道纵向超声导波检测传感器.仪表技术与传感器，2004(11):3－4.

［8］王雪梅，倪文波，王平.高速铁路轨道无损探伤技术的研究现状和发展趋势.无损检测，2013，35(2):10－17.

［9］焦敬品，钟茜，王炯耿，等.窄板中超声导波传播特性试验研究.工程力学，2013，30(7):255 －261.

［10］阎石，张海凤，蒙彦宇.Lamb波频散曲线的数值计算及试验验证.华中科技大学学报(城市科学版)，2010，27(1):1－4.

［11］何存富，李隆涛，吴斌.超声导波在管道中传播的数值模拟.北京工业大学学报，2004，30(2):129 －133.

［12］郑祥明，赵玉珍，史耀武.兰姆波频散曲线的计算.无损检测，2003，25(2):66 －68.

［13］TAWEEL H，DONG S B，KAZIC M.Wave reflection from the free end of a cylinder with an arbitrary cross－section.International Journal of Solids and Structures，2000，37(12):1701 －1726.

［14］HAYASHI T，ROSE J L.Guided wave simulation and visualization by a Semi－ Analytical Finite Element Method.Materials Evaluation，2003，61(1):75 －79.

［15］HAYASHI T，SONG W J，ROSE J L.Guided wave dispersion curves for a bar with an arbitrary cross－section，a rod and rail example.Ultrasonics，2003，41:175 －183.

［16］COCCIA S，BARTOLI I，MARZANI A，et al.Numerical and Experimental Study of Guided Waves for Detection of Defects in the Rail Head.NDT＆E International，2011，44:93 －100.

［17］BARTOLI I，MARZANI A，SCALEAA F L，et al.Modeling wave propagation in damped waveguides of arbitrary cross－section.Journal of Sound and Vibration ，2006，295:685 －707.

［18］LOVEDAY P W.Measurement of modal amplitudes of guided waves in rails.The International Society for Optical Engineering，2008，6935(69351J):1－8.

［19］LOVEDAY P W.Guided wave inspection and monitoring of railway track.J Nondestruct Eval，2012，31:303 －309.

［20］LEE C M，ROSE J L，CHO Y.A guided wave approach to defect detection under shelling in rail.NDT＆E International，2009，42(3):174－180.

［21］HESSE D，CAWLEY P.Surface wave modes in rails.Journal of the Acoustical Society of America，2006，120(2):733 －740.

［22］HESSE D，CAWLEY P.A single probe spatial averaging technique for guided waves and its applica－ tion to surface wave rail inspection.IEEE Transactions on Ultrasonics，2007，54(11):2344 －2356.

［23］LU C，MEN P，LI L L.An experimential study EMAT ultrasonic surface waves modes in rail head.International Joural of Applied E-lectromagnetics and Mechanics，2010，33:1127 －1133.

［24］卢超，李诚，常俊杰.钢轨轨底垂直振动模式导波检测技术的实验研究.实验力学，2012，27(5):593 －600.

［25］CHANG J J.Nondestructive Evaluation for Bottom Edges of a Rail using Guided Wave.2011年全球华人无损检测技术高峰论坛，厦门，2011.

［26］HAYASHI T，MIYAZAKI Y，MURASE M.Guided wave inspection for bottom edge of rails.Review of Progress in Quantitative in NDE，2007，26:169 －175.

［27］SANDERSON R M，SMITH S D.The Application of finite element modelling to guided wave testing systems.Insight:Non－Destructive Testing and Condition Monitoring，2002，44(6):359 －363.

［28］何存富，刘青青，焦敬品，等.基于振动模态分析的钢轨中超声导波传播特性数值计算方法.振动与冲击，2014，33(3):9－13.

［29］GHARAIBEH Y，SANDERSON R，MUDGE P，et al.Investigation of the behavior of selected ultrasonic guided wave modes to inspect rails for long － range testing and monitoring.Proc.ImechE Vol.225 Part F:Rail and Rapid Transit，2010，44(2):311 －324.

［30］HAYASHI T.Guided wave dispersion curves drived with a semianalytical finite element method and its application to nondestructive inspection.Japanese Journal of Applied Physics ，2008，47(5):3865－3870.

［31］ROSE J L，AVIOLI M J，MUDGE P，et al.Guided wave inspection potential of defects in rail.NDT＆E International，2004，37:153 －161.

［32］吴斌，邓菲，何存富.超声导波无损检测中的信号处理研究进展.北京工业大学学报，2007，33(4):342－348.

［33］SCALE F L，MCNAMARA J.Measuring high － frequency wave propagation in railroad tracks by joint time－frequency analysis.Journal of Sound and Vibration，2004，273:637 －651.

［34］MCNAMARA J.Health monitoring of railroad tracks by elastic －wave based on non－destructive testing.PhD Dissertation，San Diego:Unive－rsity of California，2003.

［35］SCALEA L，MCNAMARA J.Ultrasonic NDE of railroad tracks:air－coupled cross－sectional inspection and long－range inspection.Insight，2003，45(6):394 –401.

［36］BARTOLI I，SCALEAA F L，FATEH M，et al.Modeling guided wave propagation with application to the long－range defect detection in rail－ road tracks.NDT＆E International，2005，38:325 －334.

［37］KAPPATOS V，SELUCK C，GAN T H，et al.Decreasing the influence of dispersive wave modes in long－range ultras－ onic rail testing using wavelets.5th IET Conference on Railway Condition Monitoring and Non－Destructive Testing，Derby，United kingdom，2011.

［38］GURVICH A K，SAMOKRUTOV A A，SHEVALDYKIN V G.Guided wave ultrasonic flaw detection in rails Application Experience［EB/OL］.(2011－08－10)［2014 －04 －27］.http://www.ndt.net/article/ecndt 2006/doc/We.4.5.4.pdf.

［39］WILCOX P D，PAVLAKOVIC B N，EVANS M J，et al.Long range inspection of rail using guided waves.Review of Progress in Quantitative in NDE，2003，22:236 －243.

［40］SCALEA L，RIZZO F，COCCIA P，et al.Non － contact ultrasonic inspection of rails and signal processing for automatic defect detection and classification.Insight，2005，47(6):1–8.

［41］COCCIA S.Ultrasonic guided waves for structural health monitoring and application to rail inspection prototype for the Federal Railroad Administration .San Diego:University of California，2007.

［42］MARIANI S，NGUYEN T，PHILLIPS R R，et al.Noncontact ultrasonic guided wave inspection of rails.Structural Health Monitoring，2013(12):539－548.