依托旋转研究极限，函数思想破解难关

☉江苏省南京市六合区实验高级中学 王安寓

依托旋转研究极限，函数思想破解难关

☉江苏省南京市六合区实验高级中学 王安寓

“直线与圆”是解析几何的重要组成部分，其地位同圆锥曲线.很多考试都会命制质量上乘的考查直线与圆的位置关系的题目.求解直线与圆的位置的关系的题目，最关键的是灵活转化——将题目所给的条件灵活转化为相关的式子，要能透过表象看透本质，看透命题人的目的，看透命题人想考查的知识点，看透命题人想考查的数学方法，应用之求解.

题目1 （2014年江苏南通五校联考，18）已知△ABC的三个顶点A（-1，0）、B（1，0）、C（3，2），其外接圆为圆H.

（1）求圆H的方程；

（2）若直线l过点C，且被圆H截得的弦长为2，求直线l的方程；

（3）对于线段HB上的任意一点P，若在以C为圆心的圆上都存在不同的两点M、N，使得点M是线段PN的中点，求圆C的半径r的取值范围.

易求得：（1）x2+（y-3）2=10；（2）x=3或4x-3y-6=0.

本文主要研究第三问.

分析1：由（1）知H（0，3）.解析几何的一个特点是数形结合.首先作出适合题意的图形，如图1，观察图1，我们发现：此题中圆心虽定，但半径不定——圆C在动；点P动带动M、N动，而且M、N的位置对于一个点P还可能有第二种可能.四个动的元素间还没有一个定其余随之定的关系，而是既相互干扰又有变动.初读题，觉得无从入手，找不到切入口.重新读题，想到MN是圆的弦，而圆中既变（位置）又不变（长度）的弦是直径，是不是从圆的直径入手？点P是线段HB上的动点，是不是优先考虑HB的端点？连接HC、BC，易知|HC|＞|BC|，取CH的靠近C的三等分点M0，以C为圆心，以|CM0|=为半径作圆，延长HC，与圆C交于N0，则|HM0|=|M0N0|，适合题意（如图2）.当P是线段HB上任意一点时（不与H重合），连接PC并延长，与圆C交于M1、N1两点，则|PM1|＜|HM0|=|M0N0|= |M1N1|，可将PM1N1绕P旋转，则PM1变长，M1N1变短，到某一位置PMN，必有|PM|=|MN|，即该圆C适合条件.随着圆C的半径增大总可以用旋转的方法找到适合题意的割线PMN；而当圆C的半径太大时，直线HB与圆C不相离，不存在割线，不合题意；当圆C的半径太小时，连接HC，与圆C交于M2、N2两点，则|HM2|＞|M2N2|，而M2N2是圆C的最长的弦，无论怎样旋转都不会有|HM2|=|M2N2|，不合题意.从而求得圆C的半径的范围是

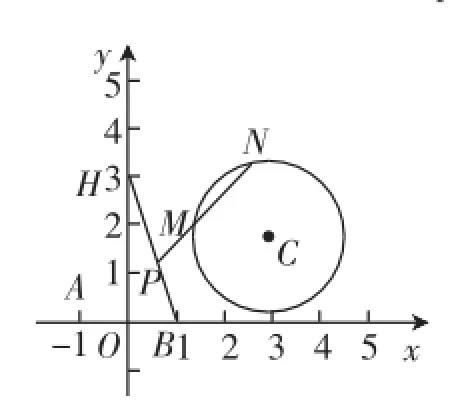
图1

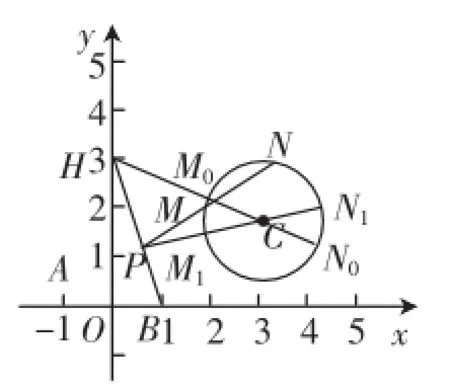
图2

解析1：见分析1.

分析2：∀P∈HB，都有P在圆C外，得|CP|-r＞0.|PM|= |MN|如何转化？注意到MN是圆C的弦，因此联系圆C的直径，必有|MN|≤2r，PM是线段HB上任意一点与圆C上一点连线的长度，自然与圆心C有关，依据三角形中两边之差小于第三边得|CP|-r≤|PM|，从而形成不等式链0＜|CP|-r≤|PM|=|MN|≤2r，再考虑∀P∈HB，自然转化为最值求解.

解析2：依题意得0＜|CP|-r≤|PM|=|MN|≤2r，即r＜|CP|≤3r恒成立.

分析3：从代数的角度思考，求出BH的方程，设出P、N的坐标，应用中点公式求得M的坐标，进而考虑M、N在圆C上，转化为两个圆有公共点问题，再转化为函数的最值问题求解.

解析3：易求得直线BH的方程为3x+y-3=0，设P（m，n）（0≤m≤1），N（x，y）.

因为该方程组有解，所以两个圆（以（3，2）为圆心、以r为半径的圆和以（6-m，4-n）为圆心、以2r为半径的圆）有公共点，所以2r-r≤≤2r+r.

易求得f（m）=10m2-12m+10，m∈［0，1］的值域为

点评：解析1是依托运动（旋转）找到解决的方法.解析2是由点P在圆C外得|PC|-r＞0，由三角形两边之差小于第三边和圆的弦中直径最长，得到PC-r≤PM，MN≤2r，再由条件M为NP的中点沟通，形成一个不等式链，通过恒成立达到解题的目的，这种求解的想法是源于前面的分析，是通过特殊到一般才形成的解题过程.∀P∈HB，都有r＜|CP|≤3r成立，自然运用函数思想，转化为最值问题求解.求解的过程简单，而思维的过程艰难.解析1呈现复杂而学生易于理解；解析2呈现简单而学生不易想到.如果把解析1的求解过程缩减，用相关的数学式子表征，那么就得到解析2.解析1是解析2的动态演示.解析3是从代数的角度入手，将点点、点圆的位置关系通过式子表示出来，进而转化为函数的最值问题求解.解析3是解析2的代数化.

变式1：已知点B（1，0）、H（0，3）、C（3，2），P为线段HB上任意一点，过点P作以C为圆心的圆的割线PMN，与圆C交于M、N，设M为PN的中点，则由所有满足上述条件的圆C组成的图形的面积为______.

变式2：已知点B（1，0）、H（0，3）、C（t，2），P为线段HB上任意一点，过点P作以C为圆心、以为半径的圆的割线PMN，与圆C交于M、N，设M为PN的中点，则实数t的取值范围是_________.

变式3：已知点B（1，0）、H（0，3）、C（2，s），P为线段HB上任意一点，过点P作以C为圆心、以为半径的圆的割线PMN，与圆C交于M、N，设M为PN的中点，则实数s的取值范围是_________.

变式4：已知点B（1，0）、H（0，3）、C（t，s），P为线段HB上任意一点，过点P作以C为圆心、以为半径的圆的割线PMN，与圆C交于M、N，设M为PN的中点，则所有适合条件的圆心C的轨迹所构成的图形的面积是________.

变式5：已知点B（1，0）、H（0，3）、C（t，s），P为线段HB上任意一点，过点P作以C为圆心、以为半径的圆的割线PMN，与圆C交于M、N，设M为PN的中点，则所有适合条件的圆的轨迹所构成的图形的面积是________.

变式6：已知点B（1，0）、H（0，3）、C（3，2），P为线段HB上任意一点，过点P作以C为圆心的圆的割线PMN，与圆C交于M、N，设（λ＞0，λ为已知的数），则圆C的半径的取值范围是_________.

高考链接

题目2 （2014年江苏，18）如图3所示，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区.规划要求：新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥两端O和A到该圆上任意一点的距离均不少于80m.经测量，点A位于点O正北方向60m处，点C位于点O正东方向170m处（OC为河岸），tan∠BCO=

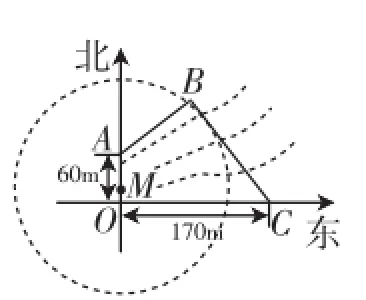
图3

（1）求新桥BC的长.

（2）当OM多长时，圆形保护区的面积最大？

题 目 3 （2011年 江 苏 ，14） 设 集 合 A=≤（x-2）2+y2≤m2，x、y∈B =（｛x，y）|2m≤x+ y≤2m+1，x、y∈R｝，若A∩B≠Ø，则实数m的取值范围是_______.

题目4 （2012年江苏，12）在平面直角坐标系xOy中，圆C的方程为x2+y2-8x+15=0，若直线y=kx-2上至少存在一点，使得以该点为圆心、1为半径的圆与圆C有公共点，则k的最大值是_________.

题目5 （2013年江苏，17）在平面直角坐标系xOy中，点A（0，3），直线l：y=2x-4.设圆的半径为1，圆心在l上.

（1）若圆心C也在直线y=x-1上，过点A作圆C的切线，求切线的方程；

（2）若圆C上存在点M，使|MA|=2|MO|，求圆心C的横坐标a的取值范围.

直线与圆的呈现千姿百态、百媚千娇，其求解过程美不胜收、令人流连，其答案驭繁于简、合理平实.如果再深层探究，那么会更摇曳生姿，会变换得美轮美奂，会让你进入另一个仙景——圆锥曲线景观.

1.王安寓.圆背景 椭圆题 推陈出新淡出奇［J］.中学数学（上），2013（9）.A