题高一尺 技高一丈
——立体几何三视图、直观图新题“破题法门”
☉浙江省湖州市第二中学 金伟兵
题高一尺 技高一丈
——立体几何三视图、直观图新题“破题法门”
☉浙江省湖州市第二中学 金伟兵
人教版《普通高中课程标准实验教科书(数学必修2)》中,空间几何体的三视图和直观图的内容约2课时,第一课时学习1.2.1中心投影与平行投影和1.2.2空间几何体的三视图;第二课时学习1.2.3空间几何体的直观图,此部分内容是在学习空间几何体的结构特征之后,在尚未学习点、直线、平面的位置关系的情况下教学的,可以为立体几何部分的学习奠定基础,有利于培养学生学习立体几何的兴趣.这块内容的教学目标是让学生能通过“实物模型—三视图—直观图”这样一个相互转化的过程认识空间几何体,是培养学生空间想象能力的有效途径,而只有奠定了空间几何体的认知基础,立体几何的教学目标才更加全面.但目前的教学现状是:按照“空间几何体”整体教学容量,留给“空间几何体的三视图和直观图”仅有2-3个课时的教学时间,很多内容在教学处理上往往被迫“点到为止”,而实际考查时却往往对这块内容的要求又比较灵活,出题也比较新颖,学生解题时最终容易陷入困境.所以如何提高此部分内容教学的针对性和有效性就显得颇为关键,笔者通过观察近年来高考三视图、直观图部分涌现出的一些新题,借此谈谈解决此类“变题”“巧题”的“破题法门”.
一、熟练“剑招”能破题
熟悉和掌握三视图、直观图问题中的基本原理和常见解法是我们解决此类问题的基础,可以说是“防身基本剑招”,主要有两方面.
“剑招”1:利用三视图、直观图中的基本“心法”,回避“还原”过程
三视图基本画图原理,我们可以总结为“长对正,高平齐,宽相等”,即主视图与俯视图的长对正(长相等),主视图与侧视图的高对正(高相等),俯视图与侧视图的宽必须相等.而直观图画法中,特别重要的一定要注意“横同,竖半,45°”,即建立45°斜二测坐标系,与坐标轴平行的线段保持平行,水平线段等长,竖直线段减半.熟记“心法”会让我们在实际解题中化繁为简,游刃有余.

图1
例1 (2014年高考北京文科第11题)某三棱锥的三视图如图1所示,则该三棱锥的最长棱的棱长为_________.
评析:本题虽只要求解三棱锥的最长棱,实质上需要对原几何体的具体结构和相应线段长全面把握,整体上我们容易发现此几何体是一条侧棱垂直于底面的三棱锥,而其中难点是如何确定底面三角形的形状,这里需要对三视图中“斜线段”到“直线段”的变化特别敏感,根据平行投影的基本原理,我们可以得到侧视图的下底长实质上是底边三角形的边在垂直方向上的投影,从而得到底面是个等腰直角三角形,这对一般学生的直观想象能力是个挑战.但如果利用基本“心法”:俯侧宽相等,则比较容易得到该几何体俯视图的高即为侧视图的底边长,所以最终求得最长的棱长为,利用基本“心法”可以巧妙回避三视图到直观图这一复杂的“还原”过程.
“剑招”2:熟记平面几何和基本空间几何体相关性质、公式,有助于快速解题
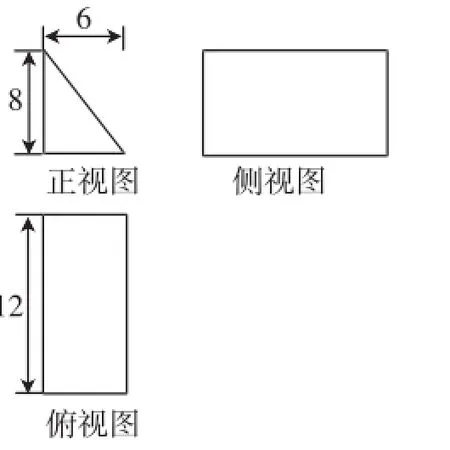
图2
三视图、直观图问题中,经常涉及平面几何相关知识点,如相似三角形、勾股定理等,同时也特别喜欢和柱、锥、台、球等常见几何体的面积、体积问题进行交汇命题,这就需要在平时的学习中熟练掌握相关的平面几何性质、表面积和体积公式等,这有助于我们迅速地找到思路,求解问题.
例2 (2014年高考湖南卷第7题)一块石材表示的几何体的三视图如图2所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于( ).
A.1 B.2 C.3 D.4
评析:由图可得该几何体是一个三棱柱,原问题即等价于在此几何体中找最大的内接或内切球,这个问题是三视图、直观图、柱和球多个知识点间的交汇,若熟练掌握平面几何性质,则可转化为平面几何问题,即求三个视图中内切圆面积谁最小,可发现是正视图,其半径为r==2,则其所对应的内切球最大半径即为2,从而迅速求解.
二、借助“法宝”巧破题
“法宝”1:以长方体作为背景模型利于“还原”
近年的“变题”中,对三视图题的直观图“还原水平”要求较高,往往很多是“不规则放置”的几何体,对学生的空间想象能力是极大的挑战.由于三视图是平行投影,因此若能引入长方体或正方体作为背景模型进行研究,把它的下、后、右侧面作为“投影幕布”,在还原过程中会收到奇效.
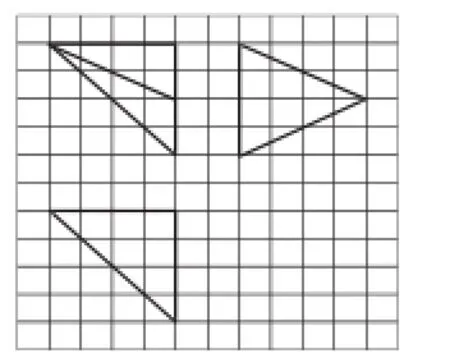
图3
例3 (2014年高考全国1理科第12题)如图3,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( ).


图4
评析:本题对空间想象能力要求比较高,由三个视图的形状可判断该多面体为四面体,但具体放置的角度比较难以想象,而由于长、宽、高均是4个单位,所以我们可以把几何体放置在棱长为4的正方体中研究,如图4所示,由俯视图可知四面体必位于正方体右上角部分空间,4个关键顶点中应取后面4点中3点,且上下棱各至少取1点,再由正、侧视图想象,另一顶点必位于前面右边棱的中点,连接即可得到.把四面体放置在正方体中研究,以后、下、右侧三个面作为投影“幕布”,想象平行光的照射投影,非常利于直观图的生成.
“法宝”2:“切橡皮”模式的巧妙转化
对于某些“残缺”几何体的直观想象,借助实际或想象中的橡皮来进行切割,不失为一个好办法.
例4 (2013年高考浙江理科第12题)若某几何体的三视图(单位:cm)如图5所示,则此几何体的体积等于________cm3.

图5

图6
评析:本题所给图中若去掉正、侧视图中的中间斜线,则可以发现是一个三棱柱,在这样的基础上,若我们借助三棱柱形的橡皮进行想象切割,则很快能发现“切”掉的是如图6所示的左上角锥体,从而利用三棱柱的体积减掉三棱锥的体积得到答案24,在此想象的过程中充分借助“切橡皮”的模式,有效地推进了空间直观感觉的生成,不失为一个妙招.
三、修炼“内功”稳破题
“内功”1:提高空间想象力的“内在修为”
高手对决,再厉害的剑招、法宝也敌不过“内功”修为的高深,要解决三视图、直观图不断涌现的“新题”“变题”,提高自身空间想象力的“内在修为”才是根本,而辩证唯物主义认为,任何事物的变化发展都有其内在规律,空间想象力的提高也是如此,它是逐步、逐级向上的,有明显的层次性.教师要把握好这一规律,将其渗透到平时的具体教学实践中,真正有效提高学生的空间想象能力,方是正道.在具体教学手段上,根据空间想象力的培养规律,首先应强化学生对三维空间的认知,高中学生已经具备二维空间(平面)的知识,对三维空间的感知也有,但对三维空间的无限性、复杂性认识不够,因此,通过比较平面内与空间中两直线位置关系的不同;通过认识线面关系、面面关系来逐步强化学生对三维空间的认识就显得比较合理和重要.其次,可以培养学生对空间几何图形(体)的分解、组合和变形的想象能力,因为这一能力的实质是对空间图形中点、线、面位置关系和数量关系的认识和想象.在这一过程中,可以大胆想象,深入剖析,在解决典型问题的过程中逐步提升自己的想象能力.有了对三维空间的较强的直观认知,学生解决问题的能力自然而然会获得提高,这跟武功修为是一个道理,内功深厚,招式就成了辅助,自然能克敌制胜,得心应手.
“内功”2:让模型意识“深入人心”
数学问题中对建模非常重视,三视图、直观图问题中常见模型也很多,在平时若能摸透这些基本模型,对其基本构造和特征有深刻认识,则必然能提高解题水平,熟与不熟,透与不透,这也是“内功”之一.比如,我们可以在平时教学中经常展示模型,引导学生认识生活中的原型,并让学生想象看不见的部分,想象线面继续延伸后的状态,提高对空间几何图形(体)的感知水平,同时重视对直观图的作图能力和制作模型能力的培养,如针对常见的柱、锥、台体,规范作图,甚至可以制作简单模型,这对提高对模型的熟悉程度非常有利,同时在制作过程中逐步建立常见几何体的直观认知,也是增强内功的一个好方式.另外,可以总结一些常见模型,如正(长)方体基本构造型;棱锥(柱)基本构造型;“三节棍”型几何体,以及各种常见柱、锥、台体的组合体,摸透这些基本空间图形和几何体的差别和关联,让这些模型的形象深入我们的“内心”,解题的时候对三视图、直观图的想象能力自然得到提升.总之,在训练中增强模型意识,让头脑中累积的丰富“题型素材”变成我们解决问题的一个宝库,再复杂的空间几何体也将不再令我们感到头痛.
总之,空间几何体的三视图和直观图在培养学生空间想象能力方面具有非常重要的作用,为立体几何的后续学习提供了基础保障,如果我们能熟练掌握其中的解题基本“剑招”,巧妙借助一些解题“法宝”,更重要的是在这个过程中,最终修炼提高我们空间想象力这一本质“内功”,面对层出不穷的“新题”“变题”“怪题”,也将不再恐惧,解题时自然也就游刃有余.A

