辨析问题本质 活化解题思维——一道椭圆问题的课堂探究

☉江苏省如东县马塘中学 陈宝霞

辨析问题本质 活化解题思维
——一道椭圆问题的课堂探究

☉江苏省如东县马塘中学 陈宝霞

一、问题展示

（1）略.

（2）是否存在直线l，使得点B在以线段AC为直径的圆上？若存在，请求出直线l的方程；若不存在，请说明理由.

二、课堂实录

师：圆锥曲线问题是高考重点及难点之一，寻找恰当的解题思路是问题顺利求解的关键，高考考查的题型可谓常考常新，题型虽然千变万化，但总有其规律可循，请同学们思考一下解答圆锥曲线问题的通用方法是什么？

生1：高考对圆锥曲线问题的考查大多以直线与圆锥曲线相交为背景，通用的方法是设出直线的斜率k，得出直线方程，设出交点坐标，将直线方程与曲线方程联立，代入消元后得到含x的一元二次方程.因直线与曲线有两个交点，故方程有两根，即判别式大于0，结合根与系数的关系，得出两根之和、两根之积关于k的关系式.

师：条件清晰，思维严谨.还有没有细节需要补充？

生2：在引入直线方程之前，应对直线斜率存在与否进行分类讨论；直线方程的引入因所给的条件不同，除了可设为y=kx+b外，有时还可将方程设为x=my+n，这样可简化计算；所给的曲线如为双曲线，则代入消元后，得到一元二次方程，其二次项系数不能为0等.

师：那么此题如何处理呢？请思考.

生3：判断点B是否在以AC为直径的圆上，我们通常的做法是判断∠ACB是否可能为直角，即BA与BC是否垂直，而对于垂直问题常用的做法是判断kBC·kBA是否等于-1，或是否为0，再结合上述通法解答问题.

师：具体如何操作？

生3：（2）由题意可设直线l的方程为x=my-1，A（x1，y1），B（x2，y2）.

……

师：我们在解答解析几何题时经常会碰到这样的情况，往往能找到某种解题思路，却因为运算量过大而不得不放弃自己的解答，或者解题思路“差之毫厘”，使得问题的解答“谬以千里”.大家能顺着生3的思路进行下去吗？

生4：我觉得生3的思路可以继续下去，但需要转变一下，在△ABC中，欲判断∠ABC是否为直角，可通过判断其他角，如∠ACB是钝角还是锐角，若其为钝角，则∠ABC不可能为直角，则这样的直线不存在，若∠ACB为锐角，则可能存在使得∠ABC为直角的直线.

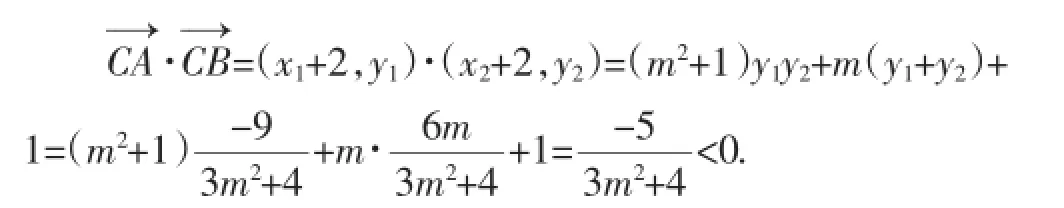
所以点B不在以AC为直径的圆上，即不存在直线l，使得点B在以AC为直径的圆上.

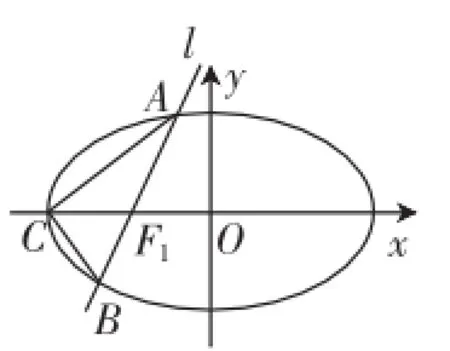
图1

师：此解法从我们熟悉的问题的解决方法入手，既落实了通性通法，又不拘泥于通法的形式.是否还有其他解法？

生5：因为直线AB经过点F1（-1，0），故向量可用向量来代换.

由题意知C（-2，0），F1（-1，0），设B（x0，y0）（-2＜x0＜ 2），则

师：此解法可谓一针见血地揭示了问题的本质所在，打破常规的解题思路，使问题得以圆满解决.数学通法是解决某一类数学问题时通用的解题方法，同学们在学习中要善于根据不同的题型，归纳出通用的解题方法，但在具体应用其解题时，要不拘泥于通法的形式，要量题而行.

三、变式演练

变式：如图2，焦点在x轴上的椭圆C过点（0，1），且离心率为Q为椭圆C的左顶点.

（1）求椭圆C的标准方程.

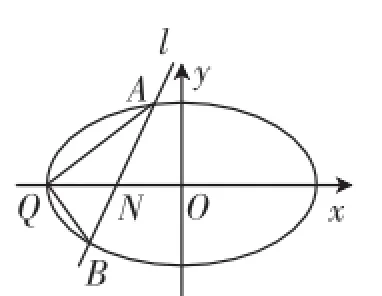
图2

（2）由（1）得Q（-2，0）.设A（x1，y1）、B（x2，y2）.

当直线l与x轴不垂直时，由题意可设直线AB的方程为y=k

由消去y得（25+100k2）x2+240k2x+144k2-100=0.

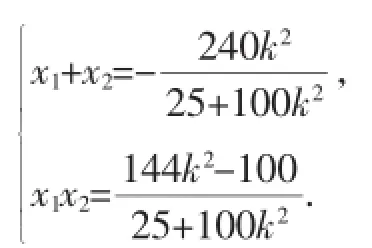
所以

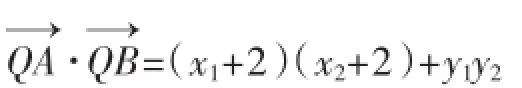
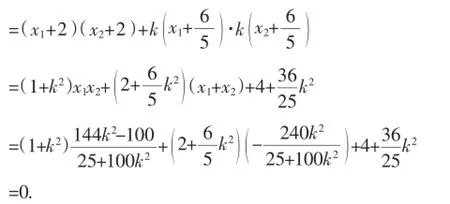
假设存在直线l使得△QAB为等腰三角形，则|QA|= |QB|.取AB的中点M，连接QM，则QM⊥AB.

所以当直线l与x轴不垂直时，不存在直线l使得△QAB为等腰三角形.

评注：在（2）的求解中，易想到的一种思路是：设A（x1，y1）、B（x2，y2），QA的中点D，利用kBD·kAQ是否为-1来判断|BQ|=|BA|能否成立.再利用是否为0，来判断∠ABQ是否为直角，进而陷入解题误区.本题借助生4的解题思想，可将问题求解.

新课程下高中数学的教学，要求教师不仅要有启发研究、诱发才能的能力，而且要能通过深入挖掘知识，培养学生提出问题、解决问题的能力.教师在课堂上要把握问题性原则，问题的设计要注意新颖性和层次性，尽力营造民主、开放的课堂氛围，学生与学生、教师与学生之间实现观点的多向交流；同时要把握学生主体性原则，为学生提供在课堂上独立活动的时间和空间.F