把握命题特色合理优化解题
——一道导数高考模拟题亮点赏析
☉江苏省常熟中学 曹正清
把握命题特色合理优化解题
——一道导数高考模拟题亮点赏析
☉江苏省常熟中学 曹正清
众所周知,函数与导数部分内容在全国各省市高考命题中均以把关题甚至是压轴题形式出现.函数的应用是考查的重点,导数已由解决问题的辅助工具上升为解决问题必不可少的工具,特别是在研究函数的单调性、极值和最值、零点,以及曲线的切线问题中,导数的作用更是功不可没.
下面以一道导数高考模拟题为例,就问题的解答谈几点意见和建议,供大家参考.
(Ⅰ)求函数f(x)的零点及单调区间;
在高考试题中导数问题的考查常以函数与导数、不等式的综合为主线,着重考查学生的数学素养和处理问题的能力,引导数学教学立足于数学知识、能力的基础上,提升学生的综合能力,导数压轴题的命制与实施,目的就是全面考查考生对数学知识的理解和能力的提升.
一、落实基础,突出能力
利用导数研究函数的单调性是导数的重要应用之一,解题中要注意对函数定义域的优先考虑,导函数的零点是否为极值点,要做充分性判断,即极值点两侧导数值异号.当x变化时,f′(x)、f(x)的变化情况如下表:


f(x)0,e ()f′(x)-f(x)↘3 3()∞3 2 e 2e2,+ 0 +↗
评注:此类问题的另一命题视角是给出单调性判断参数的取值范围,即函数在给定区间内单调递增或单调递减,则导函数在给定区间内恒大于等于0,或小于等于0,进而将问题转化为不等式恒成立问题求解.
变式1:(2015年北京海淀二模)已知f(x)是定义域为R的偶函数,当x≤0时,f(x)=(x+1)3ex+1,那么函数f(x)的极值点的个数是().
A.5B.4C.3D.2
解析:当x≤0时,f′(x)=3(x+1)2ex+1+(x+1)3ex+1=(x+ 1)2ex+1(x+4),令f′(x)=0,得x=-4,所以当x∈(-∞,-4)时,f′(x)<0,f(x)单调递减;当x∈(-4,0)时,f′(x)>0,f(x)单调递增,所以x=-4为极值点.
函数f(x)为偶函数,所以当x>0时,x=4为极值点.
又因为在x=0时,左右两侧函数单调性相异,故x=0为极值点.答案C.
评注:本题部分考生错选答案D,漏掉x=0为极值点的情况,即忽视函数极值点存在的充分条件,不可导点仍然可能为极值点.
二、把握知识关联

细心的考生已经注意到了,此时的g′(x)恰好是第一问的f(x),这也是本题亮点之一,能有效考查考生对知识关联的掌握及灵活应用的程度,进而使后续问题的求解顺理成章.

三、最基本的方法解决复杂的题目
导数的几何意义:函数在某点的导数值即为在该点切线的斜率,曲线y=存在斜率为6的切线,即导函数的值域包含6.
因为x0>,所以<2,-6x0<-3.所以y0=g(x0)<-1.
四、逆向探究,执果索因

变式3:(2015年全国新课标I)设函数f(x)=ex(2x-1)-ax+a,其中a<1,若存在唯一的整数x0,使得f(x0)<0,则a的取值范围是().

解析:设g(x)=ex(2x-1),y=ax-a,由题意知存在唯一的整数x0,使得g(x0)在直线y=ax-a的下方.

如图1,当x=0时,g(0)=-1,g(1)=3e>0,直线y=ax-a恒过点(1,0)且斜率为a,故-a>g(0)=-1,且g(-1)=-3e-1≥-a-a,解得≤a<1,答案为D.
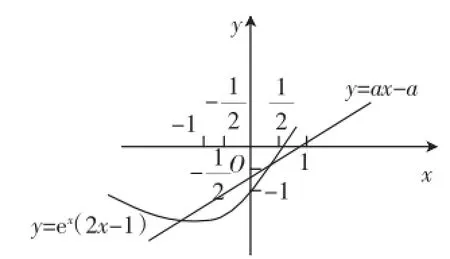
图1
本题乍一看是一个导数求最值的题目,但是因为题目中限定了“存在唯一的整数x0”这个条件,让很多同学感觉陌生和无从下手.这是默记解题套路给学生带来的思维局限.面对函数,求导只是手段而不是目的,求导是帮助我们认知一个函数的过程.题目中出现“整数”这个条件是在帮助我们简化题目,让我们只需要关注函数图像上的一些“散点”即可,但是因为高中阶段数学教学中对于离散问题研究的较少,让很多同学不适应,而忽略了问题的本质.F

