“n+n”歧义消解的博弈论模型研究*

杨 泉冯志伟

1北京师范大学汉语文化学院 北京 100875

2杭州师范大学外国语学院 浙江 杭州 311121

“n+n”歧义消解的博弈论模型研究*

杨 泉1冯志伟2

1北京师范大学汉语文化学院 北京 100875

2杭州师范大学外国语学院 浙江 杭州 311121

文章在对比典型博弈过程和歧义结构产生与消解过程的基础上,提出了一个结构歧义的博弈论模型。这个模型运用博弈论的思想和方法描述结构歧义产生及其消除过程,为歧义消解提供一种新的思路和方法。歧义消解的实例表明这种观点对我们理解和分析歧义的消解过程,提供了有益的帮助。

结构歧义 消歧 博弈论 策略

1 引言

歧义问题是语言学中的一个难点,是人与人打交道时产生误解的原因之一,更是机器翻译中的瓶颈问题,国内学者在几个不同的学术领域都对结构歧义进行过研究。

语言学界对歧义结构的研究有以下几个方面:1)研究个别歧义结构或歧义例句的语法、语义现象, 2)研究歧义结构与其它语言理论的关系,3)研究歧义结构的歧义指数与歧义度,4)研究歧义结构的产生与消除,5)对一种或几种歧义结构进行研究。

计算语言学界对歧义结构的研究主要有以下两个方面:

1 )歧义结构研究。冯志伟(1995)把他在研究科技术语结构中提出的“潜在歧义论”(PA论)进一步推广,说明在汉语日常语言中也广泛地存在着潜在歧义结构。詹卫东(1997)从计算机处理自然语言的角度着眼,指出了“PP<被>+VP1+VP2”格式对计算机造成的歧义问题,并通过归纳PP+VP组合和VP+VP组合的句法限制条件,找到了正确分析这个歧义格式的组合层次和内部结构关系的规则。詹卫东(1998)对“NP+的+VP”偏正结构的使用情况作了一番考察,概括了其句法、语义、语用特点。在此基础上分析了两个跟“NP+的+VP”偏正结构相关的歧义格式,给出了排歧办法。专门从同词性词构成短语的角度进行研究的有吴云芳(2003),主要是从句法、语义两个层面系统地研究了并列结构形成的语言规律,并列成分之间的约束关系,并对这些约束关系进行了形式化的描写。杨泉和冯志伟(2005a,2005b,2008a,2008b)在潜在歧义理论的基础上,对“v+v”、“n+n”、“v+v+v”、“n+n+n”等几种结构做了比较全面的研究,重点分析了其中动词或名词的语法、语义、语用特性,并找到了这几种结构产生歧义的原因和消解歧义的策略。

2 )歧义结构类型研究。心理学界近年来对歧义结构的研究主要从探讨人对结构歧义进行消解的心理过程入手,通过一系列实验,从另一个领域中论证了做句法结构消歧对人们更好地理解、使用句子,以及探讨句子产生的机制是非常有价值的。

本文对歧义结构进行的是一种宏观上的理论探讨,不是专门针对某个受限领域中的歧义问题进行研究,因此选取的语料是平衡的,经研究发现越是传统的,被人们立为典范的著作中,出现的实例真歧义短语越少。因此,我们的语料库是本着口语化色彩较强且可以收集到电子文本的原则建立起来的。本文收集了约100万字的语料,包括教材类、小说类、传记类、杂志类及电视新闻类。

在我们收集到的语料中可能产生歧义的结构有很多,本文仅以“n1+n2”中[+食物]类短语为例说明如何运用博弈论来消解结构歧义。从语料中提取出来的“n1+n2”结构可能产生的歧义为“定中|并列”型。例如:

两种食物一般都可以表示并列关系,这时“n1+n2”表示“n1”和“n2”是两种食物,如例(2)b中的“鸡蛋火腿”。但是“n1+n2”有时也可以表示定中关系,这时“n2”中含有“n1”,是一种食物,如例(2)a中的“鸡蛋火腿”.

上述语料中的句子都可以表示两种意思,如果在理解或者翻译的时候还原了句子的真实意思,则歧义消除,否则就会产生歧义。因此歧义消除的过程就是在遇到句子的意思有两个或两个以上的时候,如何选择其中之一以符合说话人真实意思的过程。这与经典博弈论求解最优方案在理论上是相通的。

2 “n+n”歧义结构的博弈论模型

博弈论(Game Theory)是关于包含相互依存情况中理性行为的研究。博弈论的思想及对具有博弈性质问题的研究可以追溯到19世纪初甚至更早。例如,中国著名的“田忌赛马”,三国中的“华容道”等都属于博弈论的范畴。但是一般以1944年John Von Neumann和Oskar Morgenstern合著的巨著《博弈论与经济行为》(Game Theory and Economic Behaviors)作为博弈论诞生的主要标志。20世纪50年代初,博弈论大师John Nash提出了博弈论中最为重要的解的概念——Nash均衡(纳什均衡),并证明了纳什均衡的合理性。纳什均衡适用于所有的博弈模型,为非合作博弈的一般理论奠定了基础,开辟了博弈论研究的新领域。在博弈论理论发展的同时,博弈论在军事、经济、政治等社会科学以及信息、控制、生物学、计算科学等自然科学中都得到了重要的应用。目前,博弈论不仅已经成为主流经济学的重要组成部分,甚至有学者认为它是整个社会科学的基础。

任何博弈都包括三个基本要素:1)参与人(或局中人,player),是指参与博弈的行为主体;2)战略(或策略,Strategies),每个参与人一般都有若干个战略可供选择,所有可供选择的战略构成该局中人的战略空间;3)收益(或支付,Payoff),即局中人在博弈结束后得到的利益(可能为正也可能为负),记局中人i的支付为Ui(s),s表示i个局中人的战略组合向量。显然可以看到,一个局中人的支付将不仅取决于自己所选择的战略,同样取决于其他局中人所采取的战略。

按照博弈的目的,博弈可以分为合作博弈与非合作博弈。

博弈论在经济等领域的成功运用,已经显示了其强大的作用,博弈论的理论研究也取得了很大的成功,有多位科学家因为用博弈论方法取得的成绩而获得诺贝尔经济学奖。如果我们能为自然语言处理中的一种歧义结构建立博弈论模型,就可以使用博弈论的理论和方法来分析和解决语言学中的歧义问题。下面我们以歧义结构“{牛奶咖啡}”为例来分析歧义的产生及消解过程,建立它的博弈论模型。设x={牛奶咖啡},信息发送者将x发出,当信息接收者收到x后,x有两个意思:

x1={牛奶咖啡}(定中结构,牛奶口味的咖啡);

x2={牛奶咖啡}(并列结构,牛奶和咖啡)。

他要从这两个意思中选择,如果接收者选择的意思和发送者的真实意思不一致,就产生了歧义。要消除歧义,就必须要使接收者所理解的意思与发送者要表达的意思取得一致。

从上面的分析可以看出,歧义消解的过程实际上就是信息发送者和接收者在含有多个意思的结构中相互选择确定意思的过程。如果我们把信息的发送者和接收者看作博弈的参与人,把他们可能选择的意思看作战略。显然他们在理解句意的过程中消除了歧义,则收益都为1,否则如果产生了歧义,收益为¯1。那么消除歧义的过程中具有了一个博弈过程的基本要素,因此我们可以把歧义消解过程看作一个博弈的过程。

这样我们为歧义结构“{牛奶咖啡}”建立了一个博弈论模型。在这个博弈过程中,战略空间为Θ= {x1,x2},建立该博弈的收益矩阵如图1所示。

这个博弈过程实际上是一个协调博弈问题,该问题的另一个典型的例子是左行与右行博弈,在一条路上相向而行的两个车,如果都靠左或者都靠右行,那么他们就不会相碰,假定各获得1个单位收益;但如果两个中一个靠左,一个靠右,那么他们就可能相碰,假定各获得¯1单位的收益,其支付矩阵也是图1。协调博弈是继囚徒困境博弈之后又一被广泛研究的博弈类型。为寻找解决协调问题的方法,学者们从理论上对协调博弈进行了广泛而深入的探讨。这一类型的博弈在经济和社会学中已经得到了重要应用。

3 博弈论模型的求解

在传统的博弈论中,一般都将纳什均衡作为博弈的解。

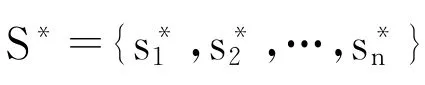
事实上一个战略组合如果不是纳什均衡,则意味着在这个组合里一定存在某个参与人(当其他参与人选择战略组合给定时),不能使自己的收益最大化。在这种情况下,理性的参与人会偏离该战略,从而使得这个战略组合不能成为博弈的结果。因此,一个战略组合如果不是纳什均衡,就不能成为博弈的解。协调博弈中存在多个纳什均衡点,参与人希望在其中任何一个纳什均衡点上实现各自的最大收益。消歧博弈有两个纯策略纳什均衡{x1,x1},{x2,x2},即双方都选择x1或都选择x2。在这类博弈中,参

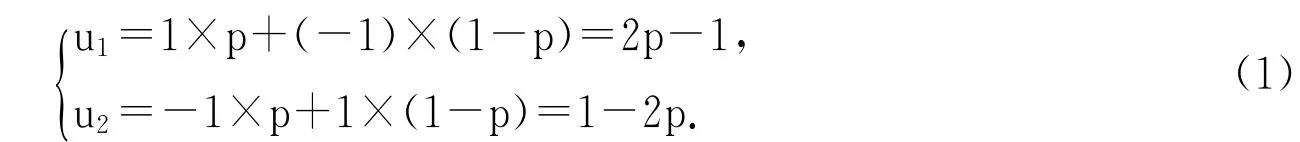
显然,接收者使自己收益最大化的一个基本选择是,当u1>u2,即p>1/2时,接收者选择x1,否则选择x2。

根据上面的选择策略,等价于选择出现概率大的那个意思,那么这个策略和传统的基于统计的歧义消除方法相同。博弈论的理论方法表明,在没有其他相关信息的条件下,基于概率的选择方法不失为一种好方法。我们将这种方法称为最大概率法,该方法的一个重要缺陷是在求解过程中使用频率较低的意思始终不会被选择,因此当发送者发送频率低的意思时总不能得到正确的理解,并且在重复多次的使用中得到同样的结果,错误永远不能得到纠正。当选择者以概率q和1-q选择x1和x2时,他的期望收益为qu1+(1-q)u2。我们希望选择一个,在发送者以不同的概率发送x1和x2时,接收者的期望收益始终非负。当接收者以与发送者相同的概率选择意思时,即令q=p,此时期望收益变为p的函数:

由f′(p)=0得,p=1/2。进一步由f″(1/2)=8>0,知p=1/2是极小值点,对应的极小值为f(1/2)=4 (1/2)2-4.5+1=0。而f(0)=f(1)=1,说明该点为最小值点。函数的最小值为零,说明函数为非负函数,因此这个策略可以满足在非负意义下的最优。采用这样的方法,不一定使期望收益最大化,可以理解为是期望损失最小。它以一定的概率在两种意思间变化,在重复执行时会得到不同的结果,能够修正错误。我们将这种方法称为基本博弈论方法。

在传统的方法中,上下文信息是进行歧义消解的重要根据。在博弈论模型的求解过程中同样也可与人在做选择时,唯一需要关心的就是其他人选择了什么,并据此做出选择。Sen(1967)将一个协调博弈称为“信心博弈”。他指出,协调博弈与囚徒困境博弈刚好相反,每个参与者选择策略A或B,仅仅需要确信对方也会相应地选择A或B。这个博弈的均衡策略中没有明显的优势策略,因此在具体的博弈过程中双方究竟选择哪个均衡还是不确定的。在实际生活中我们可以通过法律规定靠左或靠右行驶,使得交通博弈的某个均衡得以实现。在经济学领域中可以通过契约之类的东西,使得均衡得以实现。

在语言学当中,我们可以通过语法规则实现歧义消除,从而实现博弈论中的某个均衡。但是在我们研究的问题当中,语法规则已经不能进行区分。在这种情况下,两种策略无优劣之分,参与者将其多个纯策略以一定的选取概率进行组合,由此得到的均衡称为混合策略纳什均衡。例如在消歧博弈信息发送者以概率p选择x1,以概率1-p选择x2,信息接收者以概率q选择x1,以概率1-q选择x2。则两人的随机行动((p,1-p),(q,1-q))就是一个混合策略,当它满足纳什均衡条件时就是一个混合策略纳什均衡。这乍看起来似乎不可思议,实际上冯志伟(1985)已指出在人们用语言进行交际活动时,语言成分的使用会出现随机性,因此,可以使用统计的方法对其进行研究;语言统计、数理统计以及信息论等数学工具都可以用来研究语言成分出现的概率和频率,从而揭示语言的统计规律。

下面我们从信息接收者的角度分析“{牛奶咖啡}”这个歧义问题的混合策略纳什均衡。假设发送者选择x1的概率为p,则选择x2的概率为1-p。在实际应用中,接收者如何得到发送者选择某一意思的概率,一般可以从语料库中统计出每种意思出现的频率,用这个频率近似概率,作为这里的p。如果x1={牛奶咖啡}(定中结构,牛奶口味的咖啡)出现的概率为p,则x2={牛奶咖啡}(并列结构,牛奶和咖啡)出现的概率就是1-p。因此,接收者已知发送者的选择概率的假设是合理的,在此情况下接收者采取什么样的策略才能使自己的收益最大化呢?因为发送者不会始终重复地选择某个策略,这种情况下接收者不可能有合适的纯策略,他必须在两个策略之间随机选择。他以一定的概率来选择每个意思,使得自己的收益达到某种意义下的最优。接收者在该条件下选择x1和x2的期望收益分别为:以充分利用上下文的信息。博弈论的研究结果表明,解决这类无支付占优与风险占优区分的协调博弈的唯一方法是沟通。在歧义消解的过程中就是信息的发送者和接收者之间的沟通。实际上在任何语境当中,信息的发送者或多或少的给接收者发出了一定的信息,我们称为上下文信息,在博弈论中称为边信息。如果在上下文的信息中有“一份”存在,它是表示个体的量词短语,因此可以判断“牛奶咖啡”表示定中关系,是一种食物,有牛奶的咖啡;如果在上下文的信息中有“都”存在,它是表示将两种东西共存的副词,因此“牛奶咖啡”表示并列关系,是两种食物:牛奶和咖啡。如果接收者能够准确地捕捉和理解这些信息,则博弈双方就实现了沟通和协调,从而博弈可以稳定在某个均衡点上。

发送者在每次传递信息过程中对特定的类型发送特定的信息,与接收者进行沟通,接收者可以通过对这些意思的判断来选择自己的策略,达到消除歧义的目的。例如假定发送者会发送两种类型的信息x1或x2;两种类型的伴随信息m1或m2,那么接收者在收到信息m1时,判断发送者发送的类型为x1的后验概率是:

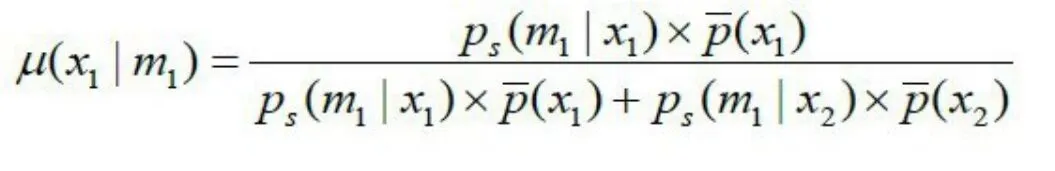
其中概率ps(m|x)表示类型x的发送者发送信息m的概率。例如当“m1=一份”时,ps=0.7,那么在这种情况下的后验概率μ(x1|m1)=90.32%,此时信息接收者选择x1,达到均衡的概率就增加到了90. 32%,这比单纯通过统计的方法要准确得多。同样我们可以计算出μ(x1|m2),μ(x2|m1)和μ(x2| m2)接收者可以根据不同的接收信息来计算后验概率,然后和先验概率进行比较,从而得出最优的行动。利用博弈论的理论和方法,我们在歧义消除过程中,尤其是在机器翻译过程中就有了具体的理论支持和可靠的操作方法,同时还有了明确度量方法好坏的标准。我们将这种方法称为包含上下文信息的博弈论方法。上述博弈论模型是根据图1所示的收益矩阵建立的,在实际应用过程中,对于一个歧义问题,它被成功消除产生的收益和歧义产生的惩罚不一定对等。它的消解结果对发送者和接收者产生的影响也不一定相等,此时收益矩阵不再是如图1所示的对等的矩阵,而是一个非对等博弈矩阵模型。如图2所示。

图2 非对等博弈矩阵

在这个博弈矩阵下,消歧的结果对双方的收益是不同的,显然也不存在纯纳什均衡,该模型仅存在混合策略的纳什均衡。接收者再根据(1)式计算自己的策略时,则得到的结果也会产生变化。显然当歧义的意思有两种以上的选择时,博弈的矩阵形式和求解的具体过程也会有相应的变化。

上面我们给出了三种消解结构歧义方法,第一种方法是根据每种意思出现的概率的大小,直接选择出现概率大的意思作为问题的解。第二种方法根据博弈论的混合策略原理进行选择。第三种方法使用上下文信息选择博弈模型的混合策略。

4 试验结果

我们将上节给出的三种方法编写程序,对从实际语料中选取出的100条包含“n+n”歧义的语料进行处理,检验它们的效果。首先我们对这些语料进行了分词和词性标注等处理。然后,对每一个“n+ n”歧义结构,统计其两种不同意思的使用频率p和1-p,根据图1的博弈矩阵建立博弈论模型。最后分别使用最大概率法、基本博弈论方法和包含上下文信息的博弈论方法对这些歧义结构混在句中进行分析处理。

我们使用三种方法对语料进行消歧,并统计每次错误数占总数的百分比。对于博弈方法由于消歧结果都是基于概率,在一次具体的使用过程中,只有对错两种具体的结果。只有对大量问题或者同一问题的反复求解中才能体现出以较大的概率选择正确结果的效果。受语料规模所限,我们用三个算法分别对这100条语料消歧,对每条语料执行10次,计算其错误百分比来得到错误率。这样也可以模拟算法对1000条语料消歧的效果。图3是每种方法的消歧情况。横坐标表示语料,纵坐标是错误百分比。

图3a 基于概率的消歧方法

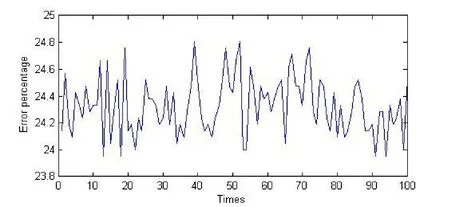
图3b 博弈论消歧方法

图3c 使用边信息的博弈论消歧方法

从图3可以看出,仅使用频率进行消歧,最大错误率在35%左右(图3a),因为10次的执行结果都相同。采取基本博弈论方法进行消歧,10次的结果各不相同,在重复的执行中有机会修正错误,因此最大错误率减少了10%左右,均小于25%(图3b)。当使用基于上下文信息的博弈论方法时,由于有了更多的信息,因此最大错误率进一步减少,达到15%左右(图3c)。

要对更加精确的模型和相应算法展开大规模和深入的实验验证,首先要有大规模的语料进行支撑。其次要对这些语料进行必要的前期处理,对不同的歧义结构出现的频率、伴随信息的数量、特征及权重等都需要进行标注。受到现实条件的限制,本文仅对语料库中出现的100条“n+n”结构的歧义现象建立博弈论模型,采取三种方法进行了消歧实验,结果证明使用博弈论的思想和方法处理结构歧义问题是行之有效的。

5 结论

信息技术的发展和大数据时代的到来要求语言处理技术不但要具有完整的理论基础,更需要能够方便在计算机上实现来处理语料数据。博弈论的迅速发展,不但具有了完备的理论分析,同时也有许多能够在计算机上方便实现的算法,在许多领域都显示了其重要的价值。本文在初步分析结构歧义产生的原因及消除歧义方法的基础上,结合博弈论的经典结果,给出了一个结构歧义的博弈论模型。理论分析和计算结论表明,该模型可以很好地描述“n+n”歧义的问题,并可以达到很好的消歧效果。使用博弈论的理论和方法不但能在歧义消除问题中应用,也为语言学的研究提供了一种新的思路和方法。

Feng,Zhiwei(冯志伟).1985.Shuli Yuyanxue数理语言学[Mathematical Linguistics].Shanghai:Shanghai Zhishi Chubanshe上海:上海知识出版社[Shanghai:Shanghai Knowledge Press].

Feng,Zhiwei(冯志伟).1995.Lun qiyi jiegou de qianzaixing论歧义结构的潜在性[On potential nature of ambiguous construction].Zhongwen Xinxi Xuebao中文信息学报[Journal of Chinese Information Processing]1995.4:14-24.

Rasmusen,Eric.2003.Games and Information(2ndedition).Oxford:Blackwell Publishers.

Sen,Amartya K.1967.Isolation assurance and the social rate of discount.Quarterly Journal of Economics 81:112-124.

Wu,Yunfang(吴云芳).2003.Mianxiang Zhongwen Xinxi Chuli de Xiandai Hanyu Binglie Jiegou Yanjiu面向中文信息处理的现代汉语并列结构研究[Study on Chinese Coordination for Chinese Information Processing].Beijing daxue boshi xuewei lunwen北京大学博士学位论文[Ph.D.dissertation,Peking University].

Xiao,Tiaojun(肖条军).2004.Boyilun jiqi Yingyong博弈论及其应用[Game Theory and its Application].Shanghai:Shanghai Sanlian Shudian上海:上海三联书店[Shanghai:Shanghai Sanlian Bookstore].

Yang,Quan(杨泉),&Zhiwei Feng(冯志伟).2005a.Mianxiang zhongwen xinxi chuli de xiandai hanyu“v+v”jiegou qiyi wenti yanjiu面向中文信息处理的现代汉语“v+v”结构歧义问题研究[“v+v”structure ambiguity study in contemporary Chinese for Chinese information processing].Yuyan Wenzi Yingyong语言文字应用[Applied Linguistics]2005.1:123-130.

Yang,Quan(杨泉),&Zhiwei Feng(冯志伟).2005b.Jiyong xiandai hanyu“n+n”jiegou qiyi yanjiu机用现代汉语“n +n”结构歧义研究[A study on the ambiguity of the“n+n”structure for computer].Yuyan Yanjiu语言研究[Studiesin Language and Linguistics]2005.4:105-111.

Yang,Quan(杨泉),&Zhiwei Feng(冯志伟).2008a.Jiyong xiandai hanyu“v+v+v”jiegou jufa gongneng qiyi wenti yanjiu机用现代汉语“v+v+v”结构句法功能歧义问题研究[Study on the ambiguity of“v+v+v”structure in con-temporary Chinese information processing].Yuwen Yanjiu语文研究[Linguistic Research]2008.4:14-20.

Yang,Quan(杨泉),&Zhiwei Feng(冯志伟).2008b.Mianxiang zhongwen xinxi chuli de xiandai hanyu“n+n+n”jiegou jufa gongneng qiyi wenti yanjiu面向中文信息处理的现代汉语“n+n+n”结构句法功能歧义问题研究[Disambiguity study of structure“n+n+n”for Chinese information processing].Hanyu Xuexi汉语学习[Chinese Language Learning]2008.6:37-47.

Zhan,Weidong(詹卫东).1997.“PP+VP1+VP2”geshi qiyi zidong xiaojie“PP<被>+VP1+VP2”格式歧义自动消解[“PP+VP1+VP2”format ambiguity automatic digestion].Zhongguo Yuwen中国语文[Studies of The Chinese Language]1997.6:424-431.

Zhan,Weidong(詹卫东).1998.“NP+de+VP”geshi zai zuju moupian zhong de tedian“NP+的+VP”格式在组句谋篇中的特点[Characteristics of“NP+de+VP”format in sentence planning].Yuyan Yanjiu语文研究[Linguistic Research]1998.1:16-23.

杨泉,女,1977年5月生,山东平度人。博士,北京师范大学汉语文化学院副教授,硕士生导师,主要从事计算语言学及对外汉语教学研究。在《语言文字应用》、《语言研究》、《汉语学习》、《语文研究》等刊物发表论文10余篇。

冯志伟,男,1939年4月生,云南昆明人。杭州师范大学外国语学院教授,博士生导师,主要从事计算语言学研究。主要著作有《自然语言的计算机处理》、《数理语言学》、《自然语言机器翻译新论》、《机器翻译研究》、《现代语言学流派》、《现代术语学引论》、《计算语言学探索》等二十几部;用中文、英文、德文、法文发表论文共200余篇。

Study of Game Theory Model of“n+n”Structural Ambiguity and Disambiguation

1Yang Quan2Feng Zhiwei

1College of Chinese Language&Culture,Beijing Normal University,Beijing 100875
2School of Foreign Languages,Hangzhou Normal University,Hangzhou Zhejiang 311121

Based on the comparison of ambiguous structures with the process of classical Game Theory,the paper proposes a Game Theory model for structural ambiguity.This model illustrates the occurrence of ambiguous structures and their disambiguation with the concepts and methods of Game Theory and provides new ways and methods to disambiguation of structural ambiguity.The illustrations of disambiguation greatly benefit our understanding and analysis of the process of disambiguation.

structural ambiguity;disambiguation;Game Theory;strategies

H087

A

1671-9484(2015)03-0250-08

2013年2月1日 [定稿日期]2014年1月17日

10.7509/j.linsci.201401.028987*《语言科学》编辑部和匿名审稿人提出了宝贵的修改意见,谨致谢忱。