对一道中考压轴题的解析与思考

☉安徽省当涂县大陇初中 倪兴隆

☉安徽省马鞍山市丹阳中学袁庆明

对一道中考压轴题的解析与思考

☉安徽省当涂县大陇初中 倪兴隆

☉安徽省马鞍山市丹阳中学袁庆明

中考压轴题的主要功能是对不同水平层次的同学进行区分和选拔，突出考查同学们在初中阶段对核心知识和重要数学方法、数学思想的理解和掌握水平.2014年安徽省中考数学压轴题（有改动），以正六边形为背景，命题的立意高、选材精、定位准；解题的入口宽、思路广、方法多，蕴含着丰富的数学思想和解题技巧，是难得的一道好题.

一、试题呈现

（2014年安徽卷第23题，有改动）如图1，正六边形ABCDEF的边长为a，P是BC边上一动点，过P作PM∥AB交AF于M，作PN∥CD交DE于N.

（1）求证：PM+PN=3a.

（2）如图2，点O是AD的中点，连接OM、ON.求证：OM=ON.

（3）如图3，点O是AD的中点，OG平分∠MON，判断四边形OMGN是否为特殊四边形，并说明理由.

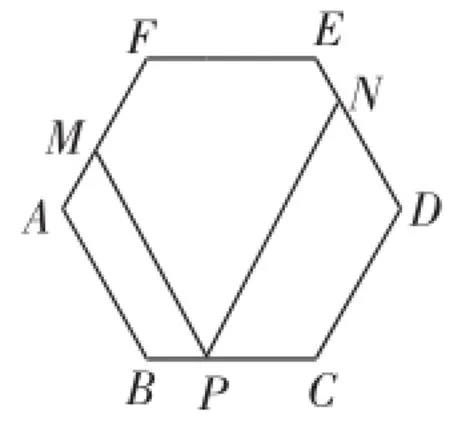
图1

图2

图3

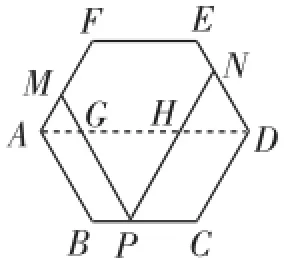
图4

二、解法荟萃

先探讨第一问的解法.

【思维导引】证明线段的和、差与倍分关系，通常采用“截长法”或“补短法”，解决本问的关键是利用转化思想，将线段PM和PN转化为正六边形的边长.

【思路分析1】如图4，通过连接AD，把线段PM和PN分割，使图中产生平行四边形和等边三角形，利用平行四边形对边相等和等边三角形三边相等的性质把线段PM和PN转化为正六边形的边长，从而完成证明.

证法1：如图4，连接AD，交PM于G点、PN于H点.

由PM∥AB，PN∥CD，六边形ABCDEF是正六边形，易知△AMG、△DHN和△PGH都是等边三角形，四边形ABPG和四边形DCPH是平行四边形，AD=2a.

PM+PN=PG+MG+PH+HN=AB+AG+CD+DH=BP+ PC+2a=BC+2a=3a.

【思路分析2】观察图形还可以发现图中存在等腰梯形，因等腰梯形两腰相等，所以还可以利用平行四边形、等腰梯形和等边三角形的性质，把线段PM和PN转化为正六边形的边长来证明.

证法2：如图4，由PM∥AB，PN∥CD，六边形ABCDEF是正六边形，易知△AMG、△DHN和△PGH都是等边三角形，四边形ABPG和四边形DCPH是平行四边形，四边形ABPM和四边形DCPN是等腰梯形，AD=2a，AM+DN=BP+PC=a.

PM+PN=MG+PG+HN+PH=AM+AB+DN+CD=3a.

【思路分析3】如图5，过B点作BG∥AM交PM于G，过C点作CH∥DN交PN于H，这样可以把PG与PH的和直接转化为BC，然后利用平行四边形对边相等把剩余两段分别转化为正六边形的边长.

图5

证法3：过B点作BG∥AM交PM于G，过C点作CH∥DN交PH于N.

由PM∥AB，PN∥CD，六边形ABCDEF是正六边形，BG∥AM，CH∥DN，得△BPG、△CPH是等边三角形，四边形ABGM和四边形DCHN是平行四边形.

PM+PN=PG+MG+PH+HN=PB+AB+PC+CD=BC+2a= 3a.

【思路分析4】连接BE，利用两个平行四边形和一个等边三角形，结合正六边形的对角线等于边长的2倍这一性质，把PM与PN的和转化为边长的3倍.

证法4：如图6，连接BE（或CF）交PM于点G.

由PM∥AB，PN∥CD，六边形ABCDEF是正六边形，得△BPG是等边三角形，四边形ABGM和四边形PGEN是平行四边形，BE=2a.

PM+PN=PG+MG+GE=BG+AB+GE=AB+BE=3a.

【思路分析5】上述几种方法是利用“截长法”来证明线段的和、差与倍分关系的，除此外还可以采用“补段法”来证明，即延长PM与PN.

证法5：如图7，分别延长PM和PN，与EF和FE的延长线分别交于G和H.

由PM∥AB，PN∥CD，六边形ABCDEF是正六边形，易知△FMG、△EHN和△PGH都是等边三角形，四边形ABPM和四边形DCPN是等腰梯形.

图6

图7

PM+PN=PG-MG+PH-NH=2GH-GF-HE=2（EF+GF+ HE）-GF-HE=2EF+（GF+EH）=2a+（GF+EH）.

易知AM+DN=a.

GF+EH=MF+NE=AF+DE-AM-DN=2a-a=a.故PM+PN=3a.

再探讨第二问的解法.

【思维导引】证明线段相等主要是通过三角形全等来证明，解决该题的关键是通过添加辅助线构造出全等的三角形.

【思路分析1】由于图中OM和ON所在的三角形显然不全等，所以必须通过添作辅助线构建全等的三角形，而垂线是常作的辅助线之一.

证法1：如图8，过O点分别作OG⊥AF，OH⊥DE，垂足分别为G和H.

由六边形ABCDEF是正六边形，OG⊥AF，OH⊥DE，易知OG=OH，AG= DH=a.

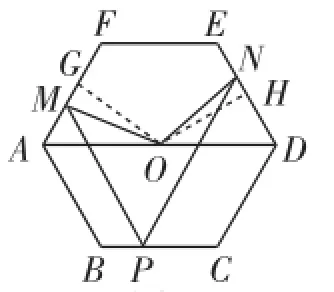
图8

图9

则△OGM≌△OHN，故OM=ON.

【思路分析2】虽然图中OM和ON所在的三角形不全等，但是若在图中标上适当的字母，就得到有可能全等的三角形，如图9中的△MGO和△OHN.

证法2：如图9，设PM、PN和AD分别交于点G和H.

易知△AGM和△DHN都是等边三角形，所以∠MGO=∠OHN=120°.

由AM+DN=a，AG+GO=a，AM=AG，DN=HN，得GO= HN.

同理，MG=OH.

则△MGO≌△OHN，故OM=ON.

【思路分析3】平行线也是常作的辅助线之一.如图10，连接BF，就有BF∥PN，这样就构建了可能全等的△AMO和△ENO.

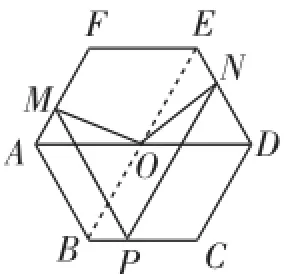
图10

证法3：如图10，连接EB（或CF）.

易知四边形ABPM和四边形EBPN都是等腰梯形，则AM=BP=EN.又AO=EO=a，∠MAO=∠NEO=60°，则△AMO≌△ENO，故OM=ON.

【思路分析4】点O既是正六边形的外心，又是它的内心，如果能够把O点转化为△PMN的外心，那么根据三角形外心的性质同样可以得到OM=ON.

证法4：如图11，连接OP和MN，过O分别作线段AB和CD的垂线l1、l2.

由l1、l2分别垂直平分线段AB和CD，四边形ABPM和四边形DCPN都是等腰梯形，得l1、l2也分别垂直平分线段MP和NP，即O是△MPN的外心，则OM=ON.

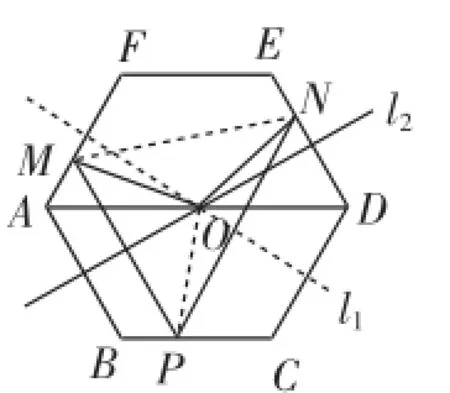
图11

【思维导引】四边形OMGN是菱形.由于根据第二问已经知道OM=ON，所以只要证明四边形OMGN是平行四边形即可.

【思路分析1】欲证明四边形OMGN是菱形，已经知道OM=ON，因此只要证明MG=ON即可（或证明OM=ON= MG=NG，利用四边相等的四边形是菱形得到证明）.

解法1：如图12，设PN交OD于H，连接EO.

由△AMO≌△ENO（图10已经证明），得∠MOA=∠NOE.又∠EOA= 120°，则∠MON=120°.

而OG平分∠MON，则∠MOG= 60°.

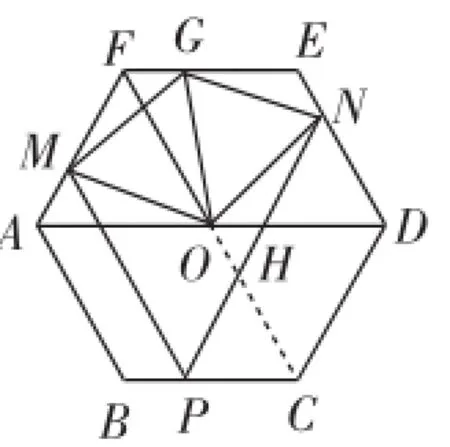
图12

则∠MOA=∠GOF，又∠MAO=∠GFO，OA=OF，则△AMO≌△FGO，则AM=FG.

又AM=BP=OH，MF=PC=DN=NH，∠MFG=∠NHO= 120°，则△MFG≌△NHO，则MG=ON.

同理MO=GN.又MO=NO（已证），则四边形OMGN是菱形.

【思路分析2】证明四边形OMGN是平行四边形，也可以根据已知120°的角，求出其他未知角的度数，从而得到对角相等来证明.根据前面的证明不难知道图13中有：△MFG≌△OKM≌△NHO≌△GEN.

解法2：如图13，易得△MFG≌△OKM≌△NHO≌△GEN，则∠FMG=∠KOM.又∠KOM+∠KMO= 60°，则∠FMG+∠KMO=60°.

又∠AMK=60°，则∠GMO=60°.

同理，∠GNO=60°，∠MGN=∠MON=120°.

图13

又OM=ON，则四边形OMGN是菱形.

【思路分析3】证明四边形OMGN是平行四边形，也可以通过对角线互相平分来证明.

解法3：如图14，连接MN.

由OM=ON（已证），OG平分∠MON，得OG垂直平分线段MN.

由MG=MO，MN垂直OG，得MN平分线段OG.

图14

则四边形OMGN是菱形.

【思路分析4】证明一个四边形是菱形，也可以利用两个全等的等边三角形拼成的四边形是菱形这一性质来证明.

解法4：如图15，连接OE、OF.

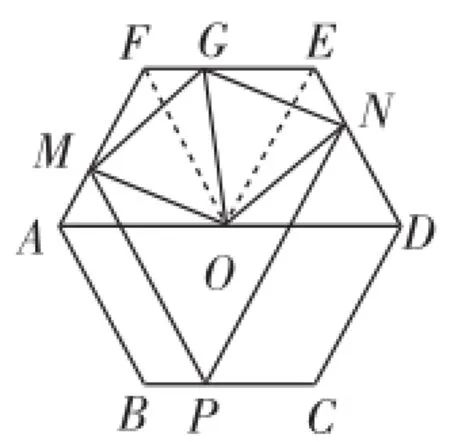
图15

由△AMO≌△ENO（图10已证），得∠MOA=∠NOE.又∠EOA=120°，则∠MON=120°.

而OG平分∠MON，则∠MOG= 60°.

又∠FOA=60°，则∠MOA=∠GOF.又AO=FO，∠MAO=∠GFO=60°，则△MAO≌△GFO，故MO=GO，因此，△MGO为等边三角形.

同理，可证△NGO也是等边三角形，故四边形OMGN是菱形.

三、模型拓展

纵观上述中考试题可以看出，它是以正六边形模型为载体，突出考查了动点定值问题和底角为60°的等腰梯形内接菱形问题.如果改变载体平台，将正六边形设计为其他的特殊图形，并将原有条件做适当调整，那么又会产生哪些结论呢？

1.关于正三角形

如图16，正三角形ABC的边长为a，P是BC边上一动点，过P作PM∥AC交AB于点M，作PN∥AB交AC于点N.

（1）思考：PM+PN的值是否变化？如果不变，则是多少？

（2）如图17，点O是△ABC的中心，连接OM、ON.试问：OM和ON相等吗？

图16

图17

参考答案：（1）PM+PN=AB=a.

（2）OM=ON.

2.关于等腰梯形

（1）动点定值问题.

如图18，等腰梯形ABCD的对角线长为b，过下底BC上一点P作PM∥AC，PN∥BD，分别交两腰AB、DC于点M、N，则PM+PN的值是多少？

图18

参考答案：PM+PN=b.

（2）内接菱形问题.

①顺次连接等腰梯形各边中点所围成的四边形是菱形吗？

参考答案：是菱形.

②如图19，已知M、N分别是等腰梯形的两腰AB、CD上的点，且BM= DN，作线段MN的垂直平分线分别交两底AD和BC于点E和F，判断四边形MFNE是否为特殊四边形，并说明理由.

图19

参考答案：四边形MFNE是菱形.

3.关于正五边形

如图20，已知正五边形ABCDE的边长为a，P是CD上的一点，PM∥CB，PN∥DE，试探究PM+PN的值是多少.

图20

四、方法提炼

深入研究上述中考题，我们会发现其中蕴含着许多数学思想方法.提炼这些方法，对我们解决各种类型的压轴题有一定的指导作用.

1.动点定值问题的探究方法

动点定值问题是近年来中考命题热点，更成为大部分学生学习的困扰.这类题型不仅考查学生对基础知识和技能的理解和掌握，对基本数学思想的领悟，更能间接而有效地体现学生数学思维的广度与深度.常见的定值问题有：线段定值、角度定值、面积定值、周长定值等.这类问题中，有时直接给出定值是何值，让我们去论证结论的正确性，但有时候却没有给出定值具体是何值，而是隐含在题设中，要我们自己去探讨，这是解决这类题的关键.而将动点位置特殊化是探究定值的一种有效办法.

2.线段相等关系的证明方法

证明线段相等关系的方法很多，主要有四种：（1）把要证的两条线段放在两个三角形中，利用全等三角形对应边相等来证明；（2）把要证的两条线段放在两个三角形中，利用相似三角形对应边成比例得到，从而证出a=b；（3）把要证的两条线段放在同一个三角形中，利用等角对等边来证明；（4）利用等式的性质，先证a=c，再证b=c，从而得到a=b.

3.线段的和、差与倍分关系的证明方法

证明线段的和、差与倍分关系，通常采用“截长法”或“补短法”，有时还会通过添加辅助线将要证的线段分解，逐步转化到一条已知线段上，从而完成倍分关系的证明.

4.特殊四边形的证明方法

欲想证明四边形为某种特殊四边形，首先要了解各种特殊四边形的从属关系，即：

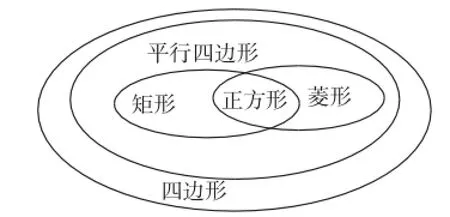
如果要证明某四边形是菱形，除了直接运用菱形的判定方法外（上述中考题第三问的证法1和证法4），也可以首先证明四边形是平行四边形，然后证一组邻边相等或证明对角线互相垂直即可（上述中考题的证法2和证法3）.

总之，中考数学压轴题具有立意新颖，知识点涵盖丰富，解题能力要求高，凸显数学思想方法，区分层次和选拔的作用，它是中考数学试题的精华部分.认真研究这样的中考试题，能够帮助学生克服畏难情绪，提升应试水平.