约束广义Birkhoff系统的Lie对称性与Hojman型守恒量
曹秋鹏
(苏州科技学院 数理学院, 江苏 苏州 215009)
约束广义Birkhoff系统的Lie对称性与Hojman型守恒量
曹秋鹏
(苏州科技学院 数理学院, 江苏 苏州 215009)
建立约束广义Birkhoff系统的微分方程,给出约束广义Birkhoff系统Lie对称性的确定方程,研究在时间不变的情况下由其Lie对称性导致的Hojman型守恒量,最后举例说明结果的应用.
广义Birkhoff系统; 对称性; 守恒量
0 引 言
自1979年Lutzky开始研究力学系统的Lie对称性与守恒量[1]以来, Lie对称性方法的研究得到了迅速的发展,并取得了一些重要的成果.梅凤翔研究了各类约束动力学系统的Lie对称性[2].其他一些学者也做了大量有意义的工作[3-4].作为Hamilton系统动力学自然推广的Birkhoff系统动力学的研究已经取得重要进展[5], 尤其在其Lie对称性研究方面已有一些有意义成果.文献[6]研究了Birkhoff系统在时间不变的无限小变换下的Lie对称性以及其导致的Lie对称性守恒量.文献[7]研究了广义Birkhoff系统的Lie对称性、对称性摄动与绝热不变量.梅凤翔在专著[8]中研究了广义Birkhoff系统的Lie对称性方法,以及广义Birkhoff系统Lie对称性直接导致的Hojman型守恒量以及间接导致的Noether守恒量.这些文献均未涉及到受约束情形下的广义Birkhoff系统的Lie对称性研究.本文进一步研究约束广义Birkhoff系统的Lie对称性,探究了在时间不变的无限小变换下Lie对称性导致的Hojman型守恒量.给出约束广义Birkhoff系统的Lie对称性的确定方程以及其导致Hojman型守恒量的条件和Hojman型守恒量的表达式.
1 约束广义Birkhoff系统的运动方程
广义Pfaff-Birkhoff-d′Alembert原理为

(1)
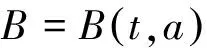

(2)
对其变分,得
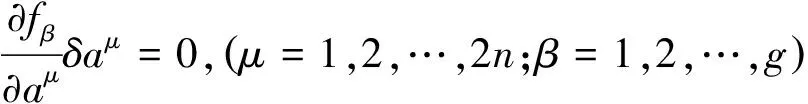
(3)
设
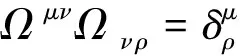
(4)

(5)
利用广义Pfaff-Birkhoff-d′Alembert原理(1)与虚位移方程(3),利用Lagrange乘子法,可得到约束广义Birkhoff系统的运动方程:
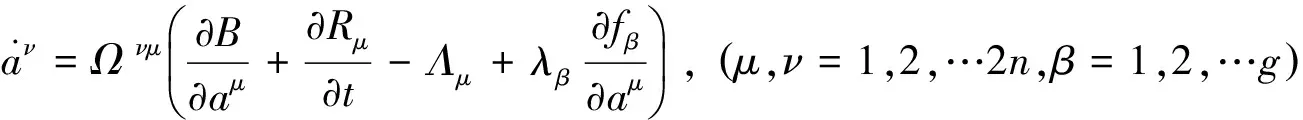
(6)
由方程(2)和(6)我们可以解出λβ.
2 约束广义Birkhoff系统的Lie对称性
约束广义Birkhoff系统的Lie对称性是指在无限小变换下的一种不变性,取无限小变换
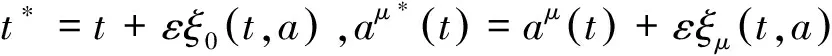
(7)
其中ξ0,ξμ为无限小生成元,ε是无限小参数.

(8)
我们可以得到如下命题
命题1 当且仅当

(9)
如果

(10)
则方程(6)在(7)式下保持不变.
由方程(8)我们将式(9)写成形式

(11)
方程(11)称为约束广义Birkhoff系统Lie对称性的确定方程,进而得到
命题2 如果无限小生成元ξ0,ξμ满足式子(11),则相应的对称性为约束广义Birkhoff系统的Lie对称性.
若时间是不变的,即ξ0=0,则Lie对称性的确定方程变成
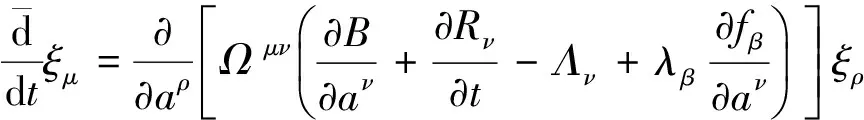
(12)
其中

(13)
3 Hojman定理的推广
对于时间不变的特殊情况下Lie对称性可导致Hojman型守恒量,我们有命题如下
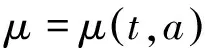
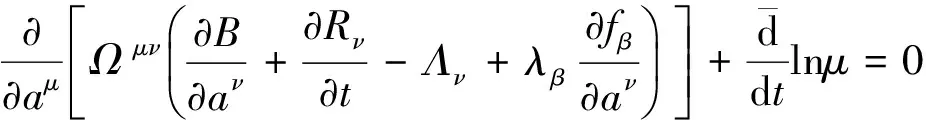
(14)
则系统有Hojman型守恒量

(15)
证明 将(15)按照方程(6)对t求导数得到
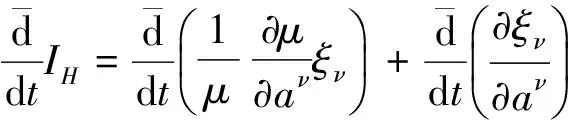
我们有以下关系成立
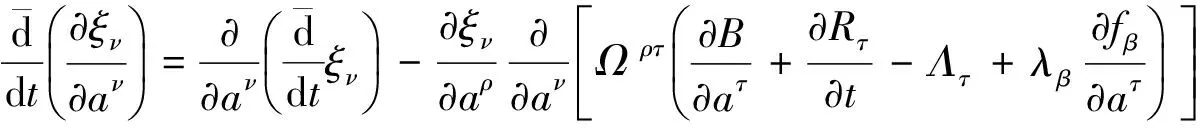
(16)
将(12)代入(16),同时利用(14)有
综上所述,质量管理系统是军工企业提高产品质量管控的主要保证,对军工企业前进与发展起着关键性影响,而当前军工产品质量管理系统在诸多方面还存在一定的不足,如部门设置、管理方式等方面,因此,结合当前现状制定合理、科学的军工产品质量管理系统优化策略至关重要,从而更好地发挥质量管理系统作用。
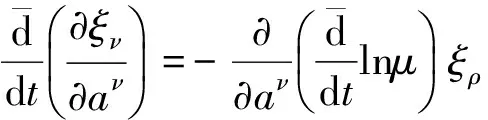
因此
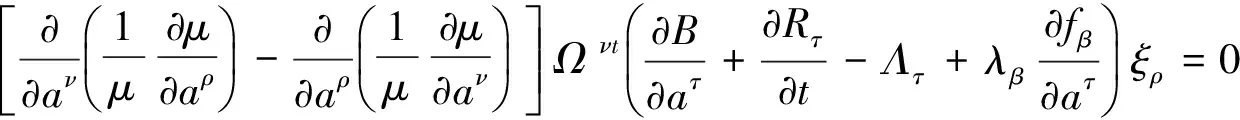
命题得证.
4 算 例
已知四阶广义广义Birkhoff系统,Birkhoff函数组和Birkhoff函数是
R1=R2=0,R3=a1,R4=a2,
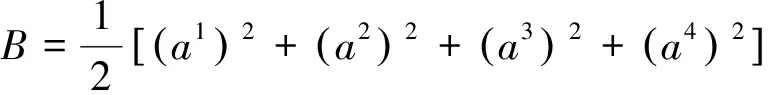
附加项为
Λ1=a1+a3,Λ2=a2+a3,Λ3=a2+a3,Λ4=a2+a4,
(17)
约束方程
f1=a1+a2=0,f2=a3+a4=0,
(18)
试由Lie对称性导出Hojman型守恒量.

由式子(6)我们得到
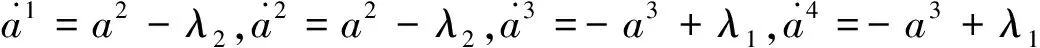
(19)
由(18)和(19)解出
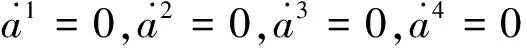
然后建立确定方程,由确定方程(12)可以得到
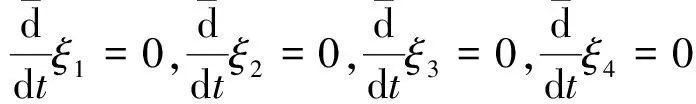
有如下解
ξ1=ξ2=ξ3=ξ4=1,
式子(14)给出
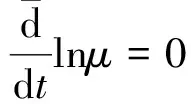
它有解如下
μ=a1,
则由守恒量(15)得到
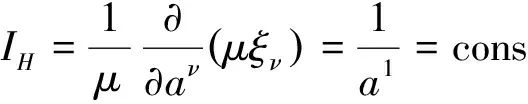
5 结 论
对于约束广义Birkhoff系统如果无限小生成元ξ0,ξμ, 满足确定方程(11), 则相应的对称性为Lie对称性.如果考虑时间不变则此时Lie对称性可导致出形如(15)式的Hojman型守恒量.
[1]LutzkyM.DynamicalSymmetriesandConservedQuantities[J].J.Phys.,A:Math.Gen.,1979,12 (7):973-981.
[2]梅凤翔.李群和李代数对约束力学系统的应用[M].北京:科学出版社, 1999.
[3]Jian-HuiF,YongP,Xiang-HongY.LieSymmetricalHojmanConservedQuantityofRelativisticMechanicalSystem[J].CommunicationsinTheoreticalPhysics, 2005, 43(6):1053-1055.
[4]HanY,WangX,ZhangM,etal.LiesymmetryandapproximateHojmanconservedquantityofAppellequationsforaweaklynonholonomicsystem[J].NonlinearDynamics, 2013, 71(3):401-408.
[5]SantilliRM.FoundationofTheoreticalMechanicsⅡ[M].NewYork:Springer-Verlag, 1983.
[6]张毅.Birkhoff系统的一类Lie对称性守恒量[J].物理学报, 2002, 51 (3) :461-464.
[7]LiYanmin.LieSymmetries,PerturbationtoSymmetriesandAdiabaticInvariantsofaGeneralizedBirkhoffSystem[J].ChinesePhysicsLetters, 2010, 27(1):010202-1-4.
[8]梅凤翔.分析力学[M].北京:北京理工大学出版社, 2013.
[责任编辑:徐明忠]
Lie symmetry and Hojman conserved quantity for a generalized Birkhoff system with constraints
CAO Qiupeng
(School of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou 215009, China)
The differential equations of the generalized Birkhoff system with constraints are established.The determining equations corresponding to the Lie symmetry are given.The Hojman conserved quantity is discussed which determined by Lie symmetry under time-invariant.In the end an example is given to illustrate the application of the results.
generalized Birkhoff system; symmetry; conserved quantity
2015-07-22;
2015-07-27
国家自然科学基金资助项目(No.11372169)
曹秋鹏(1991-), 男, 江苏南通人,苏州科技学院硕士研究生, 主要从事数学物理研究.
O316
A
1672-3600(2015)12-0034-04

