仿射Kähler-Scalar曲率为零的紧致仿射Kähler流形

姬秀, 胡传峰，崔艳丽

(1.长江大学 文理学院, 湖北 荆州 434000; 2．防空兵学院 训练部，河南 郑州 450052)

仿射Kähler-Scalar曲率为零的紧致仿射Kähler流形

姬秀1, 胡传峰1，崔艳丽2

(1.长江大学 文理学院, 湖北 荆州 434000; 2．防空兵学院 训练部，河南 郑州 450052)

仿射Kähler-Scalar曲率; Hessian流形; 仿射Kähler流形;

0 引言及主要结果

众所周知,J-C-P定理(n=2[1],n≤5[2],n≥2[3])陈述了Monge-Pogorelov方程(1)的任意严格凸光滑解一定是二次多项式.

det(fij)=1.

(1)

设x:M→An+1是由定义在凸域Ω⊂An上的某局部严格凸函数xn+1=f(x1,...,xn)给出的超曲面.李安民和许瑞伟在文献[4]中证明了:若f满足(2),则函数f一定是二次多项式.

(2)

本文我们研究下面的方程

(3)

易知,若f满足(1)或(2),则函数f一定满足(3).方程(2)意味着Kähler-Ricci曲率为零,而(3)意味着Kähler-Scalar曲率为零.

主要定理 设x:M→An+1是由定义在凸域Ω⊂An上的某局部严格凸函数xn+1=f(x1,...,xn)给出的超曲面,若(M,g)是具有0仿射Kähler-Scalar曲率的2维紧致Hessian流形,则函数f一定是二次多项式.

1 基础知识

设f(x1,...,xn)是定义在凸域Ω⊂An上的局部严格凸函数,考虑图超曲面

M={(x,f(x))|xn+1=f(x1,...,xn)，(x1,…,xn)∈Ω}

对M选取古典相对法Y=(0,0,...,1).则Calabi度量

是相对于Y的相对度量.对位置向量y=(x1,...,xn,f(x1,...,xn)) 有

(4)

余法场

U=(-f1,...,-fn,1)

(5)

下面给出一些基本公式[1]相应于度量G的联络有Chistoffel符号

(6)

Fubini-Pick张量Aijk和Weingarten张量满足

(7)

因此有相对Pick不变量

(8)

Gauss积分条件和Codazzi方程是

Rijkl=∑fmh(AmjkAhil-AikmAhjl),

(9)

Aijk,l=Aijl,k,

(10)

由(9)得Ricci张量

Rik=∑fmhflj(AmliAhjk-AikmAhjl),

(11)

定义函数

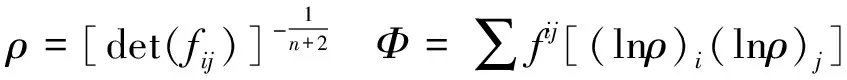
为了证明主要定理,我们先需证明Φ=0,,再利用J-C-P定理.

2 主要定理的证明

由(3)得

(12)

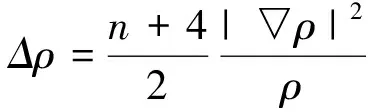
(13)

任取p∈M, 在点p的邻域取局部正交标架场, 利用(13)得

设Φ≠0取局部正交标架场使得

ρ1(p)=|gradρ|(p)>0,ρi(p)=0,∀i>1

则有

(14)

利用(13)及不等式

可得

利用Ricci恒等式得

由上述等式及(14)得

由下述方程

可得

又因为

所以

当n=2时

两边同时积分得

∫MΔΦ≥7∫MΦ2

由M紧致得

Φ=0,

利用J-C-P定理得到f一定是二次多项式.证毕

[1]Jörgens:K.ÜberdieLösungenderDifferentialgleichungrt-s2=1[J].Math.Ann.,1954,127:130-134.

[2]CalabiE.ImproperaffinehyperspheresofconvextypeandageneralizationofatheorembyK[J].Jörgens,MichiganMath.J,1958(5):105-126.

[3]PogorelovAV.OntheImproperconvexaffinehyperspheres[J].Geom.Dedicata, 1972(1):33-46.

[4]LiAnming,XuRuiwei.ArigiditytheoremforanaffineKähler-Ricciflatgraph[J].ResultMath.,2009,56:141-164.

[5]LiAM,JiaF.OntheBernsteinPropertyofAffineMaximalHypersurfaces[J].AnnalsofGlobalAnalysisandGeometry, 2003, 23:359-372 .

[6] 秦华军.仿射完备极大曲面的一个结果[J].四川大学学报, 2003(4):637-640.

[7]LiAM,SimonU,ZhaoG.GlobalAffineDifferentialGeometryofHypersurfaces,WalterdeGrayter[M].Berlin,NewYork, 1993.

[责任编辑：王军]

On compact affine Kähler manifolds with zero affine Kähler-Scalar curvature

JI Xiu1, HU Chuanfeng1, CUI Yanli2

(1.Yangtze University College of Arts and Science,Jingzhou 434000, China; 2.Department Training of the Air Defense College, Zhengzhou 450052, China)

affine Kähler-Scalar curvature; hessian manifold; affine Kähler manifolds

2015-07-17;

2015-08-09

湖北省教育厅科学技术基金资助项目(B2014281)；长江大学文理学院科研基金资助项目(201303，201304)

姬秀(1979-)，女，河南信阳人，长江大学文理学院副教授，主要从事微分几何的研究.

O174.2

A

1672-3600(2015)12-0013-03