一个极小谱任意的复符号模式

赵丽娟，邵燕灵

(中北大学 理学院，山西 太原 030051)

一个极小谱任意的复符号模式

赵丽娟，邵燕灵

(中北大学 理学院，山西 太原 030051)

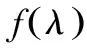
复符号模式；蕴含幂零；谱任意；幂零—雅可比

0 引 言

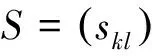
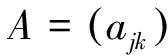
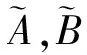
若S1=A1+iB1和S2=A2+iB2是两个n×n复符号模式矩阵，如果A2是A1的子模式，且B2是B1的子模式，则称S2是S1的子模式，也称S1是S2的母模式.若S2是S1的子模式，且S2≠S1，则称S2是S1的真子模式.

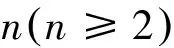
1 N-J方法

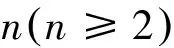
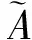
(3) 替换后的矩阵的特征多项式表达式如下：

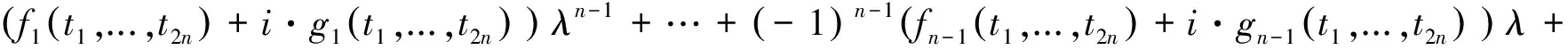
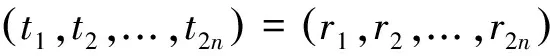
2 主要结果

(1)

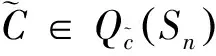
(2)

其中aj,bk为正实数，j,k=1,...,n.

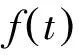
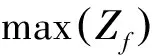
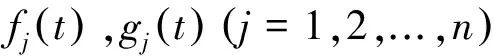
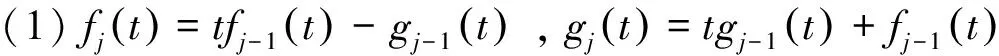
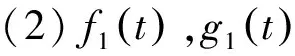
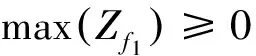
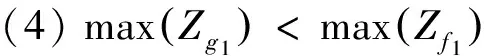
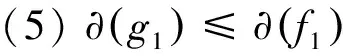
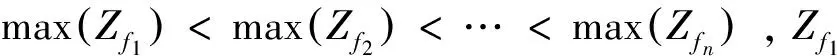
j=1,2,...,n.

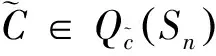
则有

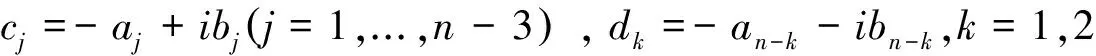
将第k行的λ倍加到第k+1行，k=1,...,n-1，再按第2,4...n-3,n-1,n列依次展开，得

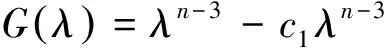
定理得证.

定理2 设Sn形如(1)，则当n≥5时，Sn及其母模式都是谱任意的.

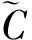
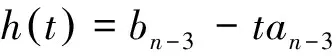
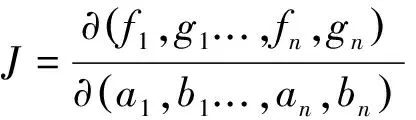
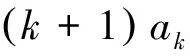
再把行列式按第1,2,...,2n-6行展开，得

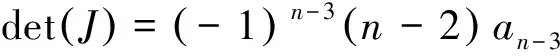
所以Sn及其母模式是谱任意的.证毕.

定理3 设Sn是形如(1)的符号模式，则当n≥5时，Sn是极小谱任意的.

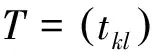
(1)显然，tkk=skk,k=1,n-2.

(2)若T所决定的定性矩阵类里的矩阵是奇异的或是非奇异的，则T都不是谱任意的，所以tk,k+1=sk,k+1,k=1,...,n-1.

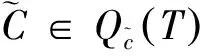
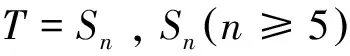
[1]DrewJH,JohnsonCR,OleskyDD,etal.Spectrallyarbitrarypatterns[J].LinearAlgebraanditsApplications, 2000, 308(1)：121-137.

[2]CaversMS,VanderMeulenKN.Spectrallyandinertiallyarbitrarysignpatterns[J].LinearAlgebraanditsApplications, 2005, 394:53-72.

[3]McDonaldJJ,StuartJ.Spectrallyarbitraryraypatterns[J].LinearAlgebraanditsApplications,2008,429:727-734.

[4]CaversMS,KimIJ,ShaderBL,VanderMeuleKN.Ondeterminingminimalspectrallyarbitrarypattern[J].TheElectronicJournalofLinearAlgebra,2005,13:240-248.

[5]BritzT,McDonaldJJ,OleskyDD,etal.Minimalspectrallyarbitrarysignpatterns[J].SIAMJournalonMatrixAnalysisandApplications, 2004, 26(1)：257-271.

[6]GaoYB,ShaoYL,FanYZ.Spectrallyarbitrarycomplexsignpatternmatrices[J].ElectronicJournalofLinearAlgebraanditsApplication,2009,18:674-692.

[7]Jia-YuShao,YLiu,Ling-ZhiRen.Theinverseproblemsofthedeterminantalregionsofraypatternsandcomplexsignpatternmatrices[J].LinearAlgebraanditsApplications,2006,416:835-843.

[责任编辑：王军]

A minimally spectrally arbitrary complex sign pattern

ZHAO Lijuan, SHAO Yanling

(School of Science, North University of China, Taiyuan 030051, China)

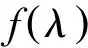
complex sign pattern;potentially nilpotent;spectrally arbitrary; nilpotent-jacobian

2015-03-04

山西省回国留学人员科研资助项目(12-070)

赵丽娟(1989-),女,山西大同人,中北大学硕士研究生,主要从事组合数学方面的研究.

O

A

1672-3600(2015)12-0008-05