借助数学软件掌握复变函数概念和函数级数

(上饶师范学院 物理与电子信息学院，江西上饶334001)

数学物理方法是解决各类物理和工程技术问题的工具[1]，涉及的内容广，对学生的数学和物理基础要求高。由于理工科专业的课程随着科学技术的迅速发展而不断增多，一方面后继专业课程对数学物理方法的内容需求发生了相应的变化，有些内容的应用价值在不断消失，可科学技术又提出越来越多需要解决的非线性数学物理问题[2]，如分形、孤立子和混沌等，丰富了数学物理方法的新内容，推动了数学物理方法自身的发展。而另一方面，由于专业课程数的增多，导致数学物理方法的平均教学时数的下降。因此，在这种形势下，研究采用合适的教学手段和方法，在有限的课时内，保证和提高教学质量具有重要的意义。

数学物理方法被公认为是一门比较抽象难学的课程，究其原因一是数学模型是具体物理模型和工程技术问题的数学描述，比较抽象；二是这些不直观的理论和求解方法难以理解和掌握；三是具体问题的数学计算往往非常复杂；四是在计算和推导过程中，需要用到较多的高等数学和大学物理中的基础知识，涉及面广[3]。近几年，我们一直在探索如何解决存在的这四个困难，找到的方法之一就是借助数学软件如Maple强大的符号运算功能解决计算和推导问题[4-6]，利用它的图像显示功能，解决数学物理方法中各种抽象的概念和公式的图像表达问题，使学生更直观地理解具体的数学物理现象，同时帮助学生掌握这些数学软件的使用方法，并将其应用到物理学和工程技术的领域中，解决具体的科学技术计算问题。显然有助于培养学生的创新能力和促进个性发展，并为学生毕业论文和设计打下良好的基础。

1 利用数学软件的图像显示功能，理解和建立形象的复变函数概念

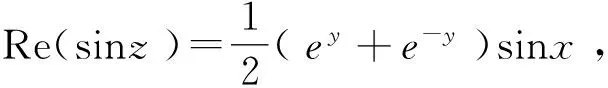
> with(plots): /加载数学软件Maple中的plots函数库,冒号指不显示加载后的结果。/

> r:=rationalize(expand(convert(sin(x+I*y),exp))); / convert是将正弦复变函数化成指数形式;expand是对表达式展开;rationalize是将复数有理化，使分母不含虚数，将实部与虚部分开;最后将经处理所得的复变函数赋给变量r。/

r1:=collect(Re(r),sin,factor); / Re是取出变量r的实部；collect是将实部按sin收集系数，并写成积的形式;将所得结果赋给变量r1。/

r2:=collect(Im(r),cos,factor); / Im是取出变量r的虚部；collect是将虚部按cos收集系数，并写成积的形式;将所得结果赋给变量r2。/

> plot3d(r1,x=-5..5,y=-2..2,axes=boxed,labels=[x,y,Re],color=[255,255,255]); /

plot3d是作出实部r1的三维图；x的取值从-5到5,y的取值从-2到2；axes=boxed 指定坐标轴围绕图形；labels=[x,y,Re] 指定坐标轴的名称为x,y和Re ；color=[255,255,255] 指定图形颜色的RGB值，为黑白，无色。结果如图1所示。/

>plot3d(r2,x=-5..5,y=-2..2,axes=boxed,labels=[x,y,Im],color=[255,255,255]); / plot3d是作出虚部r2的三维图；各参数含义同上。结果如图2所示。/

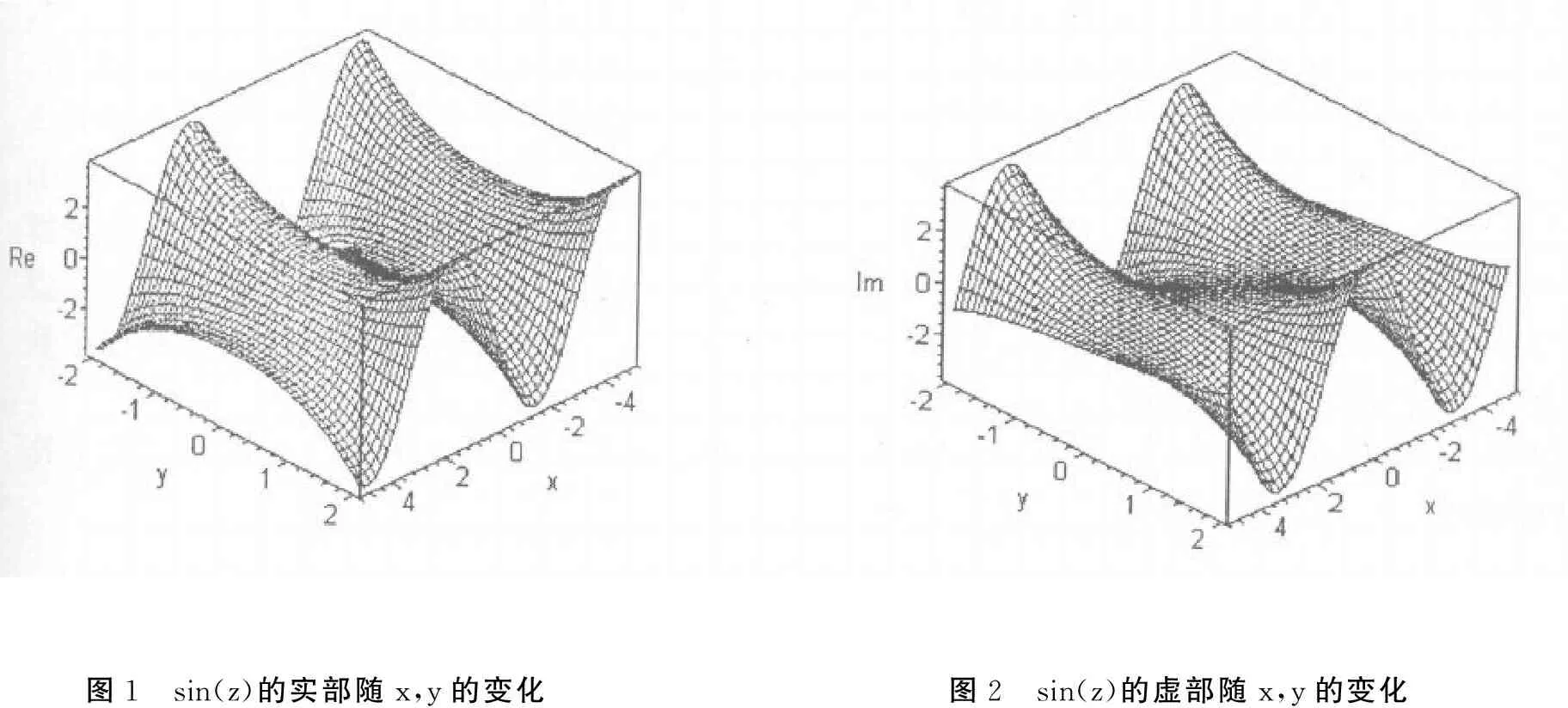
图1 sin(z)的实部随x,y的变化图2 sin(z)的虚部随x,y的变化

比较图1和图2，可知sin(z)的实部在x方向作正弦的周期变化，而在y方向按指数变化。虚部在x方向作余弦的周期变化， y方向按指数变化。

写入如下的指令，可得到sin(z) 随x,y变化的图像，如图3所示。

>complexplot3d(sin(z),z=-4-1*I..4+1*I,axes=boxed,labels=[x,y,sin(z)],color=[255,255,255]); / complexplot3d是作出复数sin(z)的三维图；z的取值从-4-1*I到4+1*I；labels=[x,y,sin(z)] 指定坐标轴的名称为x,y和sin(z) ；其它参数含义同上。/

由图3可直观看出，sin(z)随z=x+iy的实部x作周期变化，是以2π为实周期的函数，随虚部y作指数变化,其幅值可大于1，不同于实变函数sin(x)。

输入如下指令，可得双曲复变函数sinh(z)的图像，如图4。

>complexplot3d(sinh(z),z=-1-4*I..1+4*I,axes=boxed,labels=[x,y,sinh(z)],color=[255,255,255]);

由图4可直观看出，sinh(z)随z=x+iy的实部x作指数变化,而随虚部y作周期变化，是以2πi为虚周期的函数,不同于sinh(x)。

同样可画出其它三角函数、双曲函数、指数函数和对数函数的复变函数图像，有利于学生建立形象直观的复变函数概念。

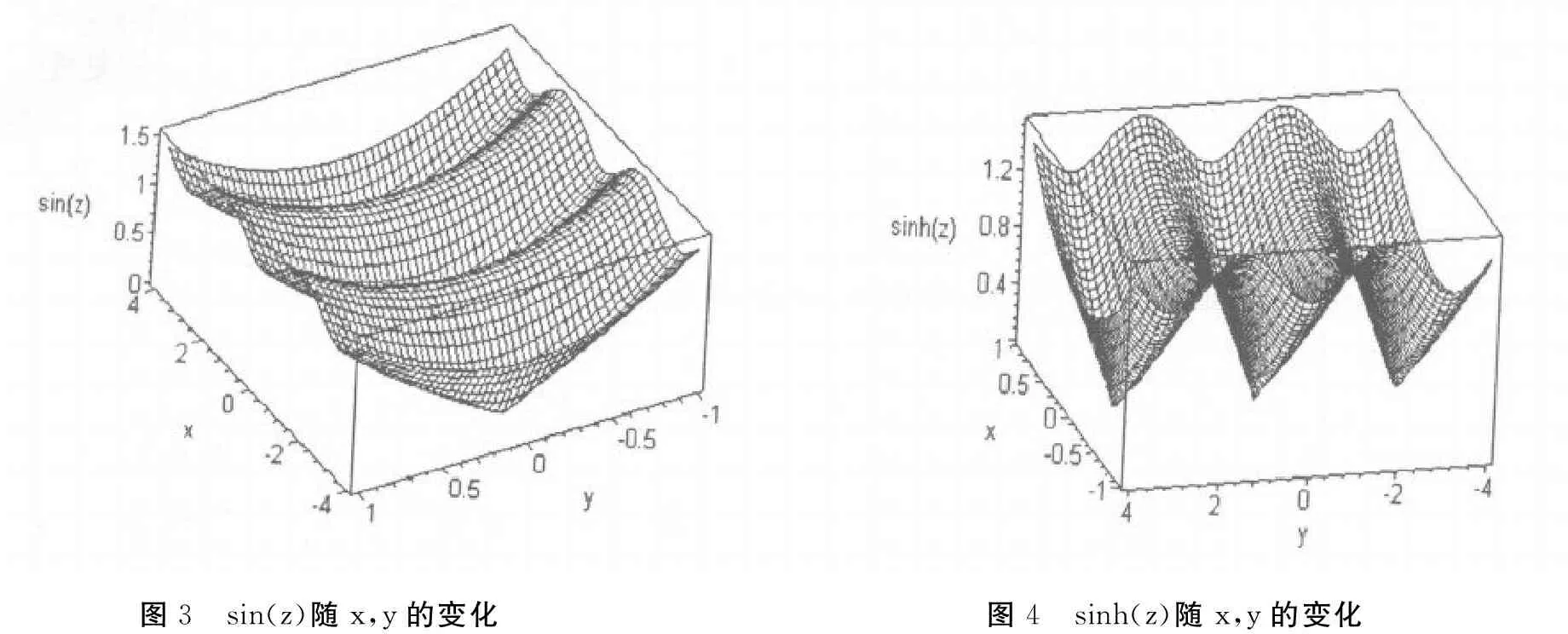
图3 sin(z)随x,y的变化图4 sinh(z)随x,y的变化

2 借助数学软件深化认识函数的级数

函数的级数作为解决物理和工程技术问题的一种理论工具，在计算积分和求解非线性微分方程的过程中，为了寻找起主要作用的物理量之间的关系，需要对其中的函数进行变换，如将一个函数用著名的幂级数、泰勒级数或付里叶级数表示。但是学生在学习和使用这种思想方法时，常常会遇到如下四道坎，一是为什么要将一个简洁的函数，用一个形式更加复杂的近似的级数表示？二是一个函数是否与级数等价，存在多大的误差？三是计算级数的系数，往往比较复杂；四是在应用过程中，将函数展开成哪种级数？有利于问题的解决，在哪点展开更合适？误差更小？对于第一个疑问，通过物理和工程技术中所遇到的困难，说明为什么要采用这种变换方法。等价与误差问题在教材中已有严格的证明和分析，但过于抽象不够直观。发挥数学软件的功能，有助于学生跨过后面三道坎。

Maple提供了幂级数、泰勒级数的展开功能，付里叶级数需要自己在Maple中写一小段程序，付里叶变换在 inttrans的函数库中。用下面二例加以分析比较。

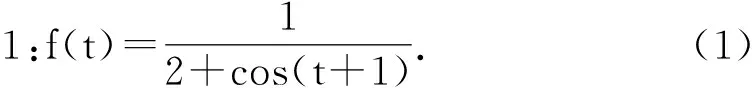
如果这个函数出现在微分方程中，很难求得精确解，甚至不可解；如果用手工计算它的积分，也不容易。所以在物理和工程技术中出现这样的函数，往往将它展开成级数进行分析讨论，寻找物理量之间的关系。首先将它展开成泰勒级数和付里叶级数，然后通过图像分析比较级数与原函数之间的一致情况。在Maple中输入如下指令：

>restart:with(plots): / restart系统复位，with(plots)加载作图函数库plots。/

>plot(1/((2+cos(t+1))),t=-Pi..Pi,linestyle=1,thickness=0,color=black);g1:=%: /画出函数1/((2+cos(t+1)))的平面图，linestyle 定义线型，1表示实线，2表示用点构成线，3表示虚线与点交错构成线；thickness 定义图线的粗细，0表示最细，数字越大，线越粗；color定义图像颜色，black黑色。g1:=%:将所得图像存于g1变量中，%表示上一次程序执行的结果。/

根据付里叶级数的定义，在Maple中编写一段付里叶级数展开的程序，存放于函数名为fseries中，指令如下：

> fseries:=proc(f,mg::name=range,n::posint)

local a,b,T,z,sum,k;

a:=lhs(rhs(mg));

b:=rhs(rhs(mg));

T:=b-a;

z:=2*Pi/T*t;

sum:=int(f,mg)/T;

for k from 1 to n do

sum:=sum+2/T*int(f*cos(k*z),mg)*cos(k*z)+2/T*int(f*sin(k*z),mg)*sin(k*z);

end do;

sum;

end:

> combine(fseries(1/((2+cos(t+1))),t=-Pi..Pi,5))：

plot(%,t=-Pi..Pi,linestyle=2,thickness=1,color=red);g2:=%: / fseries将函数展开成付里叶级数，5表示取级数的前五级，combine将所得结果进行合并，冒号不显示结果；plot画出1/((2+cos(t+1)))的付里叶级数的平面图，其中参数含义同上，图像颜色为红色；g2:=%:将所得付里叶级数的平面图存于g2变量中。/

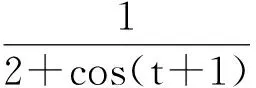
>tay：=taylor(1/((2+cos(t+1))),t=0,5); / taylor将函数展开成泰勒级数，并赋值给变量tay。/

>series(1/((2+cos(t+1))),t=0,5); / series将函数展开成幂级数。/

取出泰勒级数tay的前五项，再赋值给tay，然后作图,所得图像存于g3变量中。

>plot(tay,t=-Pi..Pi, linestyle=2,thickness=2,color=green,style=point);g3:=%:

将原函数图g1与付里叶级数的图g2、泰勒级数g3显示在同一张图中, 进行比较。

> display(g1,g2,g3); / 结果如图5。/

图5中ABCDE为原函数图线，BCD为原函数的付里叶级数图线，BCF为原函数的泰勒级数图线。由图可直观地看出，付里叶级数图线与原函数的图线很吻合，泰勒级数图线在展开点t=0附近BC段吻合，而CF段误差越来越大。可见对于周期函数展开成付里叶级数的误差比泰勒级数小。

误差的大小不但与展开级数的类型有关，与展开级数的项数有关，幂级数和泰勒级数还与展开点的选取有关。下面以非周期函数为例说明这一情况。

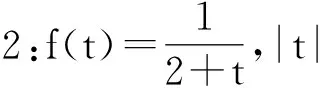
在将函数展开成级数的具体应用中，面临着选择展开的类型、阶数以及在哪个点展开等问题，不同的选择误差是不一样的。为了培养学生应用级数解决问题的能力，以(2)式为例分析比较误差的大小。用上述Maple方法将展开成泰勒级数和付里叶级数，分三种情况画出相应的图像，得到如图6-8.图中AF为原函数的图线,BE为原函数展开成泰勒级数的图线,CD为原函数展开成付里叶级数的图线，n的值表示展开成级数的项数，t的值表示泰勒级数的展开点。

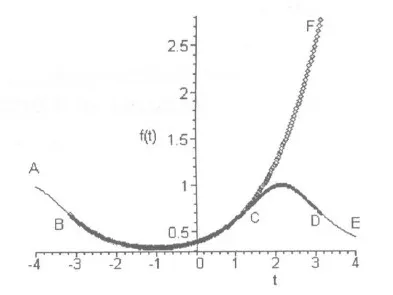
图5 原函数与展开级数的比较

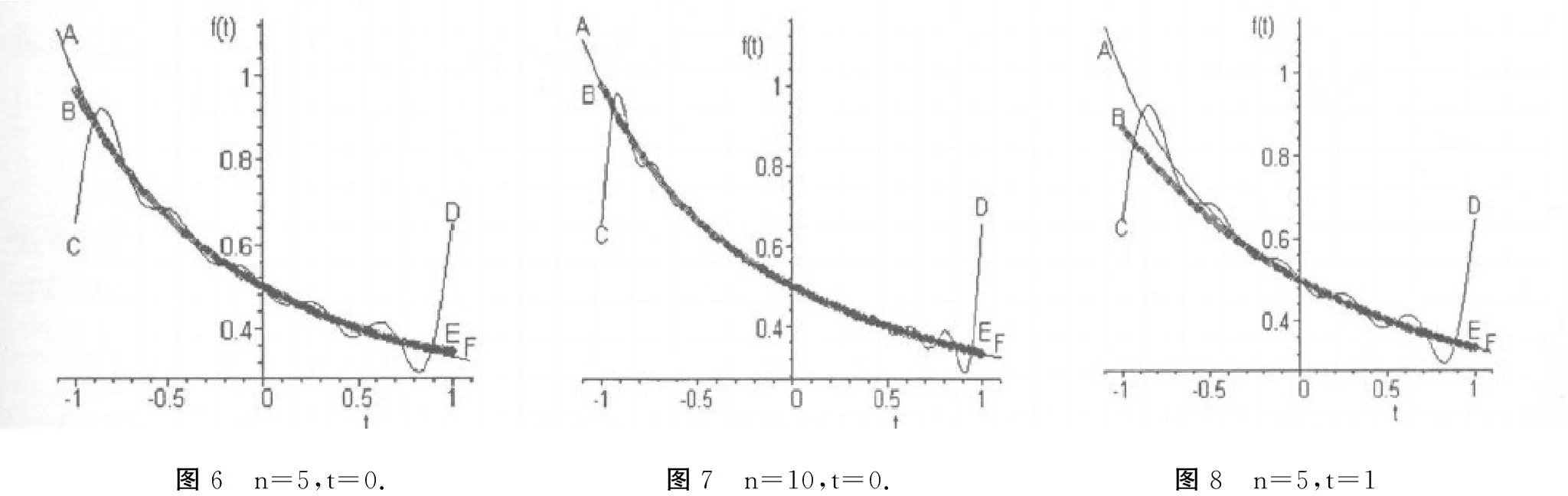
图6 n=5,t=0.图7 n=10,t=0.图8 n=5,t=1

根据图6至图8的曲线，可直观地分析结果。比较图6与图7，取展开的级数n越大，级数的曲线CD和BE越接近原函数的曲线AF,误差越小。对于非周期函数，由图6与图8可知，选择合适的展开点，泰勒级数的BE线比付里叶级数的CD线更靠近原函数的AF线，误差更小。图6的泰勒级数BE线是在t=0点展开，图8的泰勒级数BE线是在t=1点展开，其结果表明在t=1点展开的泰勒级数BE线更远离原函数的AF线，误差更大，在展开点附近的区域误差较小。可见，充分发挥数学软件在教学中作用，不但可减小繁杂的计算，而且有助于学生形象直观地理解内容，建立清晰的概念，可达到深化认识函数的级数的具体细节。

3 结论

数学物理方法是一门抽象、运算复杂、变化多的课程，用Maple中的plot、plot3d、complexplot3d等作图功能，可帮助学生理解其中的教学内容，建立清晰的概念；用collect、factor、combine、rationalize和expand等符号运算功能，可节省手工运算时间和精力，把更多的注意力集中到解决问题的方法和思路上；用fseries、taylor、series和convert等转换功能，可减小求级数系数的繁杂计算，结合作图功能，可更加深刻理解具体细节，培养和提高应用数学工具解决问题的能力。掌握一种数学软件的用法，不但可以在有限的教学时数内完成教学内容，提高教学效率，更重要的是培养学生对数学物理的兴趣，学会用先进的工具解决问题，为今后的发展打下更坚实的基础。

参考文献：

[1] 梁昆淼,刘法,缪国庆.数学物理方法[M]. 北京: 高等教育出版社, 2004.

[2] 楼森岳,唐晓艳.非线性数学物理方法[M]. 北京: 科学出版社, 2006.

[3] 马柏林，李丹衡，晏华辉．复变函数与积分变换[M]．上海：复旦大学出版社，2007．

[4] 刘琼.Maple软件在复变函她中的应用[J].邵阳学院学报(自然科学版),2013,10(1): 21-25.

[5] 阿荣．Maple在《概率论与数理统计》教学中的应用[J]．中央民族大学学报(自然科学版),2012，21(1):67-71．

[6] 周鄄川，吕同斌．Maple的图形功能在高等数学教学中的应用[J]．黄山学院学报，2010,12(3):117-119．

[7] 洪维恩,李强,董建刚.数学魔法师Maple 6[M]. 北京:人民邮电出版社, 2001.