阻尼惯性秤的定标和惯性质量的测量

(上饶师范学院物理与电子信息学院，江西上饶334001)

在大学物理实验中测量物体的惯性质量是一个基础实验，能提高大学生对物体质量的认识，并学会秤衡质量的一种新方法。在过去的惯性秤实验教学中，是研究忽略阻力作用下的惯性秤摆动周期、等效质量和附加质量块三者之间的关系[1]，虽然有利于理解摆动周期与惯性质量的关系，但不利于引导学生进一步解释惯性秤摆动幅度随时间的增大而减少的实验现象。

文献[2]建立了具有阻尼作用的惯性秤动力学方程

(1)

式中λ为空气阻力系数，K为秤臂的弹性系数，m0为秤台空载时总的等效质量，mi为附加质量，θ为秤台偏离平衡位置的角度，s为θ所对应的弧长，φ为固定的竖直平面与秤台运动平面的夹角，g为重力加速度。由此可解得摆动周期为

(2)

式中L为等效摆长。如果将秤臂秤台平面调成水平，与固定的竖直平面垂直，即φ=90°,cosφ=0，则

(3)

根据(2)或(3)式，分析讨论了阻力对周期和振幅的影响[2]。但没有提出具有阻尼的惯性秤定标和测量质量的实验方法。本文将解决具有阻尼的惯性秤定标和测量物体惯性质量的实验问题。

1 阻尼惯性秤的定标和惯性质量测量方法

由(2)式可知，由于阻力的存在λ≠0，使得周期T与质量mi失去了线性关系，出现了非线性曲线。利用传统方法对惯性秤定标的结果，将无法测量待测物体的质量。我们介绍一种借助数学计算软件Maple进行曲线拟合，对惯性秤进行定标和测量物体惯性质量的实验数据处理方法。

首先将惯性秤的秤臂秤台固定在竖直支架上，使夹角固定不变，可以不为90度。选用微秒(μs)记时器，测出惯性秤每摆动20个周期所需的时间，重复三次，结果分别记为Ti1，Ti2，Ti3。然后依次在秤台上增加已知质量块，改变mi(i=0,1,2..10)，测量对应的周期，结果如附表。表中Ti为一个周期的平均值。

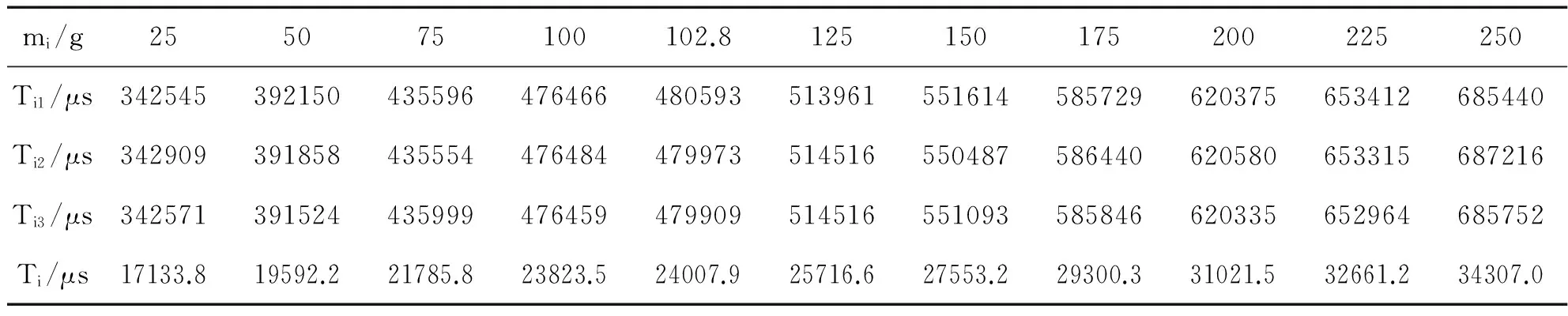
附表 用惯性秤定标已知质量块的质量与惯性秤摆动周期的实验测量结果

然后，根据附表的实验结果，利用数学计算软件Maple进行二次曲线拟合。曲线拟合或称回归，是根据二个物理量之间的实验结果，利用最小平方法，以求出最逼近或最能反映这二个物理量之间变化关系的函数，其计算方法和原理可参考文献[3]。由于曲线拟合的计算比较大，我们可以借助数学计算软件Maple进行曲线拟合。在Maple的state函数库中，有一个叫fit的子函数库，提供了leastsquare( )指令，该指令具有强大的曲线拟合功能。它有二种使用格式，一种是leastsquare[vars](data)，即以串行vars里的元素为变量做曲线拟合；另一种使用格式是leastsquare[vars,eqn,pars](data)，即以方程式eqn来拟合数据data,其中vars为eqn里的变量，而pars为变量的系数。以附表的实验结果，说明leastsquare( )这二种指令的用法，并分析比较直线拟合与曲线拟合结果的差异。在Maple中写入如下命令：

> restart: with(stats): with(fit): with(plots): with(PDEtools):

其中restart为清除内存中已有Maple的函数和变量，with(stats)、 with(fit)、with(plots)和 with(PDEtools)分别为将stats，fit，plots(作图工具函数库)，PDEtools(代数运算函数库)调入内存，冒号“:”为不显示函数库加载后的结果。将质量块的质量组成串行，赋值给变量mi，相应的指令为

> mi:=[25,50,75,100,102.8,125,150,175,200,225,250];

对附表中各质量块相应的测得周期进行计算，求出一个周期所需的时间，并组成串行，赋值给变量Ti，相应的指令为

>Ti:=[(342545+342909+342571)/60,(392150+391858+391524)/60,(435596+435554+435999)/60,(476466+476484+476459)/60,(480593+479973+479909)/60,(513961+514516+514516)/60,(551614+550487+551093)/60,(585729+586440+585846)/60,(620375+620580+620335)/60,(653412+653315+652946)/60,(685440+687216+685762)/60];

再求出一个周期的平方，组成串行，并赋值给变量ti，相应的指令为

> ti:=[T[1]^2,T[2]^2,T[3]^2,T[4]^2,T[5]^2,T[6]^2,T[7]^2,T[8]^2,T[9]^2,T[10]^2,T[11]^2];

如果以质量块的质量m为自变量，对应的一个周期的平方T为因变量，进行线性拟合，相应指令为

> eq1:= leastsquare[[m,T]] ([m[i], t[i]]);

拟合后的直线方程为

eq1：=T=0.1810375936 109+0.3917748779 107m。

(4)

如果对附表中的质量和周期的平方，进行二次曲线拟合，相应指令和拟合后的曲线方程分别为

> eq2:=leastsquare[[m,T],T=a*m^2+b*m+c,{a,b,c}]([ m[i],t[i]]);

eq2：=T=1990.599812m2+0.3365620824 107m+0.2097567093 109。

(5)

进行三次曲线拟合，相应指令和拟合后的曲线方程分别为

> eq3:=leastsquare[[m,T], T=a*m^3+b*m^2+c*m+d,{a,b,c,d}]([m[i],t[i]]);

eq3:=T=3.064306383m3+740.0860339m2+0.3508125491 107m+0.2056986520 109。

(6)

为了直观地分析讨论拟合后的曲线方程与实验结果的符合情况，先画出实验结果的图像，并赋值给变量g1

> g1:=plot(zip((m,T)->[m,T], m[i],t[i]),style=point,labels=[m,T]):

再分别画出直线方程eq1、二次曲线方程eq2和三次曲线方程eq3所对应的图像，并分别赋值给变量g2、g3和g4，对应的maple命令为

> g2:=plot(rhs(eq1), m=0..250):

g3 :=plot(rhs(eq2), m=1..250):

g4 :=plot(rhs(eq3), m=1..250):

然后将实验结果的图像g1逐一与g2、g3和g4进行比较，对应的maple命令为

> display(g1, g2); display(g1, g3); display(g1, g4);

分别得到如图1、图2和图3。

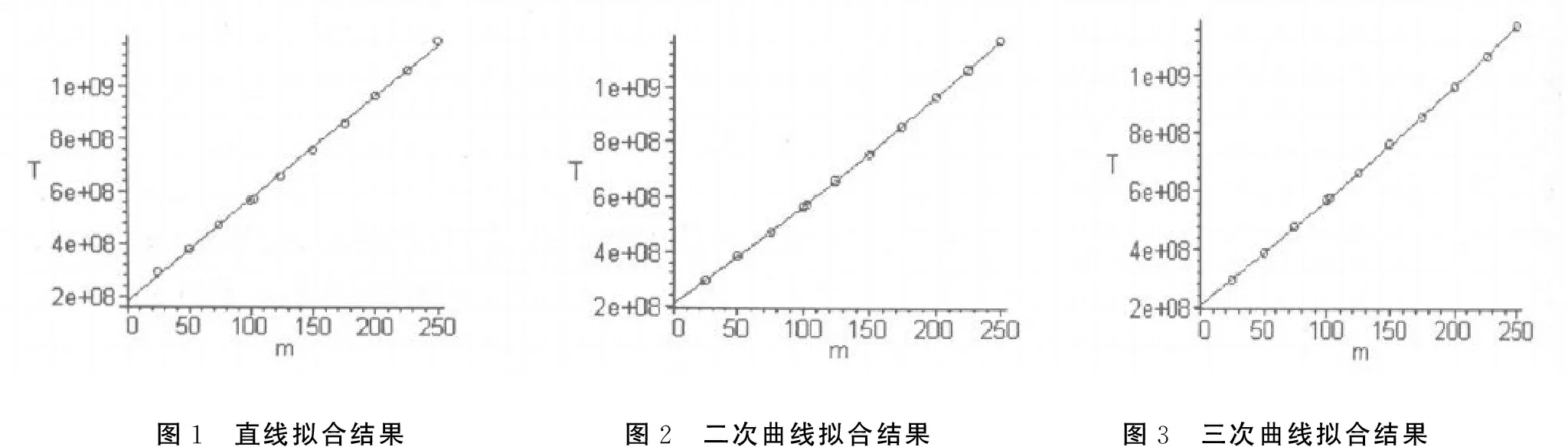
图1 直线拟合结果图2 二次曲线拟合结果图3 三次曲线拟合结果

图中横坐标m表示已知质量块的质量，纵坐标T表示质量对应一个周期的平方。空心圆圈表示实验数据点，实线表示拟合函数的质量m与一个周期的平方T的图像。

由图1可知，偏离直线的实验数据点较多，说明(4)式的直线方程

T=0.1810375936 109+0.3917748779 107m，

与实验结果误差较大。

由图2和图3可知，实验数据点均在曲线上，说明(5)式二次曲线方程

T=1990.599812 m2+0.3365620824 107m+0.2097567093 109，

和(6)式的三次曲线方程

T=3.064306383 m3+740.0860339 m2+0.3508125491 107m+0.2056986520 109，

与实验结果很吻合，误差较小。从图像上比较，看不出图2，图3拟合曲线与实验结果的误差大小的差异，精度很接近。但可通过计算相对误差比较二次曲线与三次曲线的拟合结果的差异。

如果选择(5)式求惯性质量，可用maple的solve( )命令

> solve (T=1990.600229*m^2+3365620.701*m+209756716.5,m);

能解得

(7)

式中m的单位为克，T的单位为微秒的平方。测出待测物体摆动一个周期的平方T，代入(7)式，就可求得待测物体的惯性质量m。若以表1中参考质量m=102.8克为例，将它对应一个周期的平方T=0.5763800626×109，代入(7)式，可求得mx=102.6943470克。与参考质量m=102.8克进行比较，可得相对误差为

同理，由直线方程(4)式、三次曲线方程(6)式，求得的惯性质量mx与实验结果的相对误差分别为

η2=1.85233066%， η3=0.2880873%。

可见，η1最小，η3次之，η2最大。表明二次拟合曲线(5)式最接近实验结果，三次拟合曲线(6)式次之，直线拟合(4)式最大，由此可知惯性质量与周期的平方不是线性关系，而是非线性关系，应考虑空气阻力对惯性秤摆动的影响。可取图2为惯性秤定标曲线，根据(7)式求惯性质量最准确。

2 结论

在过去的惯性秤实验教学中，忽略阻力作用，用作图法分析讨论了惯性秤定标和惯性质量的测量问题。本文考虑了阻力作用，用曲线拟合回归法研究了阻尼的惯性秤定标和惯性质量的测量方案。由于曲线拟合回归法是基于最小平方法的数据处理方法，需要对实验数据进行大量和较复杂的计算，所以我们介绍了利用数学计算软件Maple中的state函数库的子函数库fit的leastsquare[vars](data)和leastsquare[vars,eqn,pars](data)指令，用这二个指令中的一个就可根据实验结果，得到二个物理量之间的拟合曲线，作为惯性秤的定标曲线。由定标曲线则可求得待测物体的惯性质量。分析结果表明在阻尼惯性秤的定标和惯性质量测量实验中，用leastsquare[vars,eqn,pars](data)指令拟合的惯性质量与周期平方的二次曲线的函数关系更准确。本文利用先进的数学工具解决复杂的物理实验问题的方法，对老师指导实验具有有益的参考作用，对学生能起到激发学习计算软件的兴趣，并启发引导分析复杂实验现象的能力。

参考文献：

[1] 杨述武. 普通物理实验: 力学及热学部分[ M] . 北京: 高等教育出版社, 2000.

[2] 郑雪梅，黄瑛，彭莉，等.阻力对惯性秤摆动幅度和周期的影响[J] .上饶师范学院学报，2014, 34(6): 120-123.

[3] 龚镇雄. 普通物理实验中的数据处理[M]. 西安:西北电讯工程学院出版社,1985.