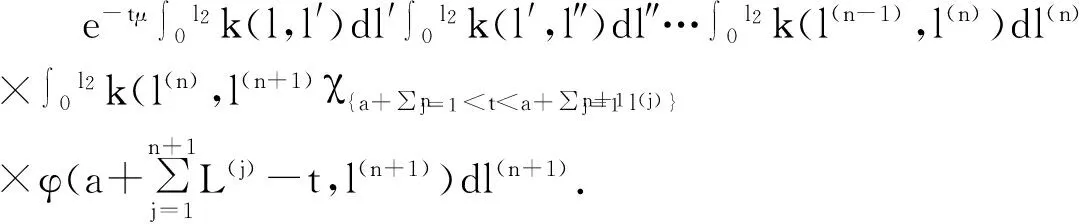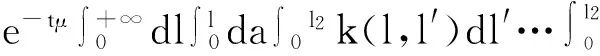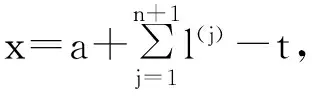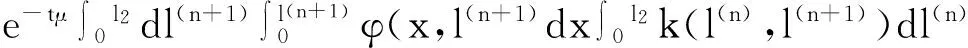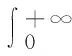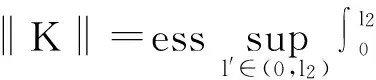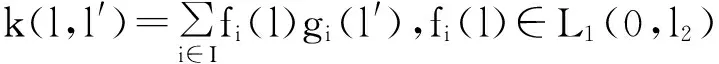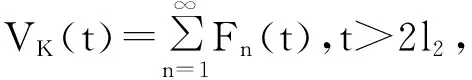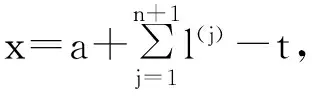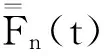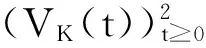紧性在L-R模型中的应用
(上饶师范学院 数学与计算机科学学院,江西上饶33400)
上世纪70年代,Lebowitz等人提出了L-R模型[1]:
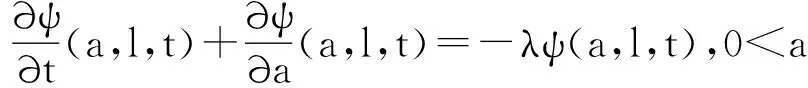
之后,该迁移方程的谱分析研究和该迁移方程解的渐近性态研究工作已成为生物数学和社会科学感兴趣的课题[2-9]。Webb在文献[2]中研究了L-R模型,在连续函数空间上,对0 无疑,对于文献[6]的条件与模型,在p=1的情况自然引起了我们的关注!本文在L1空间中研究了细胞周长为0≤l1 式中a∈[0,l]表示种群细胞的年龄,l∈(l1,l2)表示种群细胞从出生到分裂的周长,且0≤l1 定义Sobolev空间W1及其范数如下: 定义算子AK为: 假设(O)∶K是弱紧和正的边界算子,具有如下形式: 引理1.1[7]若假设(O)被满足,则算子AK在X1上生成C0半群(VK(t))t≥0. 引理1.2 设算子K是有界线性算子,算子(Kn)n是有界线性算子且满足: 证明 由引理1.1知AKq在X1上生成一C0半群{VKq(t);t≥0},因为 ‖KnMq‖≤‖Kn-K‖·‖Mq‖+‖KMq‖, 于是故此引理获证。 引理1.3 若算子K为有界正算子,当Reλ充分大时有,则有 (1.1) 其中V0(t)是由A0生成的C0半群, (1.2) 证明 由于对任意的φ∈X1,φ>0,当Reλ>-μ(其中μ=ess-infμ(.,.))有, 所以存在λ0>0,使得当Reλ>λ0时有 当n≥1时,经计算可以得到, 综上所述,此引理获证。 令Γ0={λ∈C|Reλ≥-μ}。 定理2.1 若假设(O)被满足,则‖Fn(t)‖≤e-tμ‖K‖n+1(t≥0,n≥1)。其中Fn(t)是引理1.3中所定义的算子。 证明 由于对任意的φ≥0,n≥1有, 所以, 定理2.2 若假设(O)被满足,则当t>4l2时有,算子Ak生成C0半群(VK(t))t≥0在X1空间上是弱紧算子。 证明 第1步:证明(VK(t))t≥0在t>2l2的条件下是弱紧算子。事实上,因为K是紧的,所以必定存在一列有限秩算子{Kn}n,从而得到 由于紧算子K具有如下形式: (2.1) 第2步:根据第1步知(VK(t))t≥0在t>2l2上弱紧,从而得到, 定理2.3 若假设条件(O)成立,在区域Γ0中,迁移算子AK的谱由有限个具有限代数重数的离散本征值构成,而且-∞远点是唯一可能的聚点。 参考文献: [1] Lebowitz J L, Rubinow S I. A theory for the age and generation time distribution of a microbial population [J]. Journal of Mathematical Biology,1974,1:17-36. [2] Webb G. A mode of proliferating cell populations with inherited cycle length [J]. Journal Mathematical Biology, 1986,23:269-282. [3] Latrach K, Mokhtar-Kharroubi M. On an unbounded linear operator arising in the theory of growing cell popultion[J]. Journal of Mathematical Analysis Applications, 1997,211:273-294. [4] 王胜华,程国飞. 一类增生扩散型种群细胞中迁移方程的谱问题[J]. 数学物理学报,2013,33A(1):71-77. [5] 王胜华,贾善德,黄时祥. 具扰动项的L-R型迁移算子的谱分析[J]. 系统科学与数学,2014,34(4):432-451. [6] 吴红星, 王胜华, 胡仁杰. 紧半群在种群细胞增生方程中的应用[J]. 辽宁工程技术大学学报(自然科学版), 2013,32(6): 832-835. [7] Lods B, Mokhtar-Kharroubi M. On the theory of a growing cell population with zero minimum cycle length [J]. Journal of Mathematical Analysis Applications, 2002,266:70-99. [8] Jeribi A, Megdiche H, Moalla N. On a transport operator arising in growing cell populatios II Cauchy problem [J]. Mathematical Methods in the Applied Sciences, 2005,28:127-145. [9] Dodds P, Fremlin J. Compact operator in Banach Lattices [J], Israel Journal of Mathematics 1979,34:287-320.1 预备知识
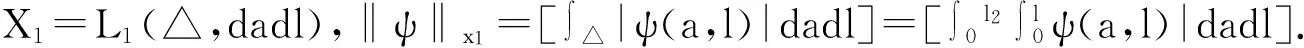
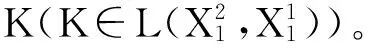
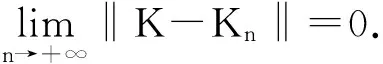
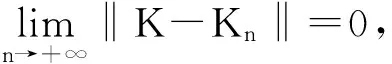
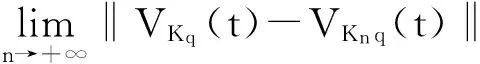
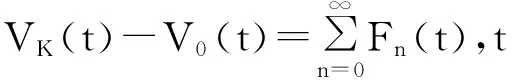
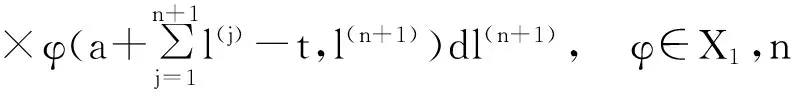
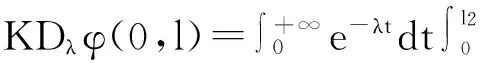
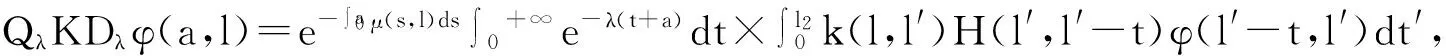
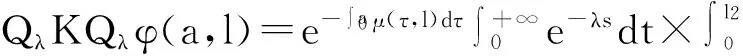
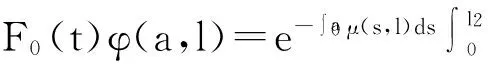
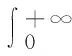
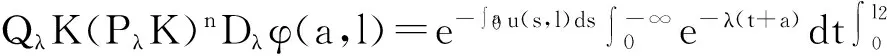
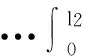
2 主要结果