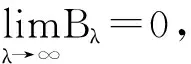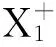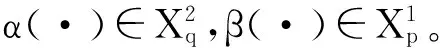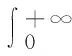具增生的细菌群体中一类迁移算子的谱分析

贾善德，程国飞，王胜华

(上饶师范学院，数学与计算机科学院，江西上饶334001)

本文研究了以下一类具增生的细菌群体中的迁移方程：

(1.1)

其中u(0

(1.2)

其中α,p≥0表示每一能有丝分解子细菌的平均数,p=1时保证了细菌通量的连续性,正核k=k(v,v')表示母体细菌V′和它的子细菌v间成熟速率的相互关系,并满足标准化条件

(1.3)

M.Rotenberg在文献[1]中提出了这类具增生的细菌群体中的迁移方程,其中仅对该迁移方程的特殊情况(即碰撞项为积分项的种群细胞的Rotenberg模型),通过使用Chapman方法,讨论了该迁移方程的数值解;之后只是对这类特殊情况有一些研究工作(部分见文献[2-8])。但是对这类具增生的细菌群体的迁移方程的研究工作很少,最近,文献[9,10]在L1空间研究了这类具增生的细菌群体模型,在边界条件α=0和边界算子为可容许算子[9,10]的情况下,得到了该模型相应的迁移算子产生不可约正C0半群,并讨论该迁移方程解的渐近行为等。但是对边界条件(1.2)中αp≠0的情况未见研究结果,因为在αp≠0时的边界算子不是可容许算子。本文在Lp(1≤p<+∞)空间上,讨论了这类模型(1.1)-(1.3)相应的迁移算子的谱分析,得到了这类迁移算子的谱在某右半平面上仅由可数个具有限代数重数的离散本征值组成等结果。

1 预备知识

本节主要给出一些本文需要的Banach空间和有关的算子及结果等。设

Xp=Lp(Ω,dudv),(1≤p<+∞)，Ω=(0,1)×(a,b)=I×J.

它们分别按范数

和

构成的Banach空间。令Yp=Lp(J,vdv)为迹空间，其范数为

引进边界空间和范数分别为

Xi=Lp(Γi,dv),i=1,2;Γ1={(0,v)∶v∈J};Γ2={(v,v)∶v∈J}.

引理2.[11]若ψ∈Wp,则ψ|Γ1∈X1的充要条件为ψ|Γ2∈X2.其中

ψ|Γ1=ψ(0,v),ψ|Γ2=ψ(1,v)

定义迁移算子A为：

其中σ(.,.)∈L∞(Ω),边界算子K为：

K∶X2→X1,Kψ|Γ2=ψ|Γ1.

对φ∈Xp,λ∈C,ψ∈D(A)考虑方程

(λ-A)ψ=φ.

(2.1)

则∀λ,Reλ>-σ(σ=essinf{σ(u,v)∈I×J}),方程(2.1)可形式地解为：

(2.2)

取u=1,则(2.2)式为：

(2.3)

根据(2.2)式和(2.3)式引进如下算子：

ψ|Γ2=BλKψ|Γ2+Eλφ.

(2.4)

ψ=DλKψ|Γ2+Fλφ.

(2.5)

2 算子A的谱

定理3.1 如果假设(O1)被满足,且存在数λ0,使得∀λ>λ0,有

rσ(BλK1)<1.

(3.1)

则迁移算子A的谱σ(A)由至多可数个具有限代数重数的离散本征值组成。

证明：由(2.4)式和(3.1)式,对λ>λ0,有

ψΓ2=Hλ·ψ|Γ2+Lλφ.

(3.2)

其中Hλ=(I-BλK1)-1BλK2),Lλ=(I-BλK1)-1Eλ。

(Hλ)2=(I-BλK1)-1BλK2(Hλ)2≤(I-Bλ2K1)-1BλK2(Hλ2)2

(3.3)

①课程知识点的学习微视频：教师根据课程的教学任务和目标，对教学内容进行梳理，把课程的知识点分割成利于微课制作的小的学习单元，每个学习单元的学习时间控制在十分钟左右，设计微教案，在设计时应充分考虑各种媒体技术的应用以增加微课的趣味性和互动性,从而激发学生的学习兴趣。同时针对不同层级的学生，可设计不同梯度的学习任务和目标，学生可根据自己学习的实际情况进行自主选择学习内容，真正实现个性化学习和差异性教学，从而较好地调动学生的积极性和主动性。

(3.4)

因此由Gohberg-Shmul'yan定理[13,p.258]知:(I-(Hλ)N)是有界可逆算子(λ∈C，λ∉S,S={λk∶k=1,2,…};λk是(I-(Hλ)N)-1的极点)。因为

I-(Hλ)N=(I-Hλ)(1+Hλ+…+(Hλ)N-1),λ∈C,λ∉S.

所以

I-(Hλ)-1=(I+Hλ+…+(Hλ)N-1)(I-Hλ)N)-1,λ∈C,λ∉S.

因此，若λ∈C,λ∉S,则方程(3.2)式变为

ψ|Γ2=(I-Hλ)-1Lλφ.

(2.5)式变为

ψ=DλK(I-Hλ)-1Lλφ+Fλφ.

又方程(2.1)式可变为

ψ=(λ-A)-1φ

于是

(λ-A)-1=DλK(I-Hλ)-1Lλ+Fλ.

(3.5)

所以λ∈S是(λ-A)-1的极点,从而σ(A)在某半平面上由至多可数个具有限代数 重数的离散本征值组成。

定理3.2 设条件同定理3.1, 若γσ(Bλ0K2)>1,则有σ(A)≠,从而存在一个最大的实有限重离散本征值证明：设λ∈σ(A)∩R,由谱映象定理([14,p.569])知:rσ(Hλ)是关于λ的连续单调递减函数,又

λ∈σp(A)⟺1∈σp(Hλ).

(3.6)

由于Hλ≥BλK2, 则有

故存在λ1>λ0,使得γσ(Hλ1)=1,因此σ(A)≠,从而由文献[15]即知本定理成立。

Γs={λ∈C|-σ≤Reλ≤s(A)}.

其中s(A)表示算子A的谱界。

定理3.3 设条件同定理3.1,则当λ∈Γ,且|Imλ|充分大时, 算子(I-Hλ)-1存在。

证明 下面分两步证明。

此外,对任一整数n,有

由控制收敛定理知：

所以

(b){K2Bλ,λ∈Γ0}是紧集。

由(a)(b)及文献[16]可得

(3.7)

所以

(3.8)

因此本定理成立。证毕。

定理3.3 条件同定理3.1,则σ(A)∩{λ∈|Reλ>-σ}仅由有限个具有限代数重数的离散本征值组成。

证明 由定理3.2知:Γs∩S在|Imλ|=+∞时没有聚点,且Γs∩S被限制在Γs的一个紧区域中,所以Γs∩S有限,从而σ(A)∩Γs有限,因此由定理3.1(1)知本定理成立。证毕。

参考文献：

[1] Rotenberg M. Transport theory for growing cell populations[J]. J theor Biol, 1983, 103(2):181-199.

[2] Boulanouar M. A transpot equation in cell population dynamics[J]. Diff Inte Equa. 2000,13:125-144.

[3] Boulanouar M. Asymptotic behavior of transpot equation in cell population dynamics with a null maturation velocity[J]. J Math Anal Appl,2000,243(1):47-63.

[4] Boulanouar M. Transpot equation in cell population dynamics (I)[J]. Elec Diff Equa. 2010, 144:1-20.

[5] Boulanouar M. Transpot equation in cell population dynamics (II)[J]. Elec Diff Equa N 2010, 145:1-20.

[6] 王胜华,翁云芳,阳名珠.人体细胞增生中的一类迁移算子的谱分析[J].数学物理学报,2010,30A(4):1055-1061.

[7] 王胜华,吴军建. 种群细胞增生中一类Rotenberg模型[J].应用泛函分析学报,2014,16(4):296-303.

[8] Wu Hongxing, Wang Shenghua, Yuan Dengbin. Spectral distribution of transport operator Arising in cell Population[J].Journal of Function Spaces ,Volume 2014, Article ID 748792, 10 pages.

[9] Boulanouar M. Transpot equation for growing bacterial populations (I)[J]. Elec Diff Equa. 2012, 221：1-25.

[10] Boulanouar M. Transpot equation for growing bacterial populations (II)[J]. Elec Diff Equa 2012, 222:1-21.

[11] Boulanouar M. A mathematical study for a Rotenberg model[J]. 2002, 265(2):371-394.

[12] Kato.T.Perturbation Theory for Linear Oprators[M].New York:Springer-Verlag,1966.

[13] Kaper H G,Lekkerkerkerker C G,Hejtmanek J.Spectral Methods in Linear Transport Theory[M].Birkhauder,Basel,1982.

[14] N.Dunford, Schwartz J T.Linear Operators:Part I[M].New York Interscience:1958.

[15] Vidav. I Existence and uniqueness of nonnegative eigenfunctions of the Boltzmann operator[J].J.Math.Anal.Appl.1968,22(1):144-155.

[16] Anselone A P, Palmer J M.Spectral analysis of collectively compact. strongly convergent operator seqences[J]. Pacific J Math 1968,25(3):423-431.