基于分数阶微积分的Q2黄土含水损伤蠕变模型

唐 皓，段 钊，赵法锁，宋 飞，李香凝

(1.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059； 2. 西安科技大学地质与环境学院，西安 710054； 3.长安大学 地质工程与测绘学院，西安 710054)

基于分数阶微积分的Q2黄土含水损伤蠕变模型

唐 皓1，3，段 钊2，赵法锁3，宋 飞3，李香凝3

(1.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059； 2. 西安科技大学地质与环境学院，西安 710054； 3.长安大学 地质工程与测绘学院，西安 710054)

为探索含水Q2黄土的蠕变特性，对Q2黄土进行不同含水状态下的三轴蠕变试验，试验结果表明随着含水率的增高，Q2黄土的流变性能增强。基于分数阶微积分构造的软体元件可描述理想的固体与流体之间材料性质的特性，选用包含软体元件在内的四元件非线性蠕变模型对试验数据进行回归计算拟合求参，并对不同含水率下的模型参数进行分析。结果显示：瞬时变形模量EH与黏弹性系数ξ1均随含水率增加呈指数形式递减；引入含水损伤变量D(ω)，计算得出各蠕变参数含水损伤演化方程，进而建立考虑含水损伤的非线性蠕变模型，通过应用试验数据对其进行验证，结果表明基于分数阶微积分的含水损伤蠕变模型能够有效地描述Q2黄土的整体流变特征，模型具有较好的应用前景。

Q2黄土；蠕变试验；含水率；非线性；损伤；蠕变模型

1 研究背景

黄土在中国具有分布范围广、连续、地层发育完整及厚度大的特点。在西北地区由黄土构成的黄土高原因其雄伟壮观而闻名于世，但由于黄土遇水很容易导致其力学性质降低，致使黄土高原地区时常发生滑坡、崩塌等地质灾害。黄土遇水发生地质灾害的成因与黄土流变特性具有较大的联系，因此，不同含水状态下黄土发生流变具有较强的研究价值。一般情况下，涉及黄土遇水发生流变主要是指蠕变，而描述黄土发生蠕变性质最主要的方式是建立其流变模型。截止目前，已有一些学者对黄土的流变模型进行了一定的研究，如通过元件组合建立线性模型；或者改进线性元件为非线性元件，构建非线性模型；再者应用损伤力学的知识，结合元件模型建立了反映黄土损伤的蠕变模型。如郭增玉等[1]应用五元件Kelvin模型描述高湿度黄土黏弹性特征，用1个Maxwell元件串联1个经验模型且并联1个塑性元件来描述黄土的黏塑性特征，最终将2个复合元件进行串联建立了描述高湿度Q2黄土的非线性流变模型；朱才辉等[2]则将Kelvin模型与Burgers模型串联构成M-B模型，模型较好地描述了压实Q3黄土的蠕变特性；谢星等[3]则在考虑损伤门槛的统计损伤基础上，应用应变等效原理，建立了考虑瞬时损伤的统计损伤流变模型，较好地描述了黄土流变的非线性特征；王东红等[4]则在谢星的基础上，将突变破坏时发生的蠕变损伤引入黄土的特性研究中，建立了考虑瞬时损伤和蠕变损伤的一维和三维流变模型。上述模型的建立主要是通过应用Kelvin模型来描述黄土的线性流变特征，而非线性流变部分则通过改进黏塑元件或者通过加入损伤演化方程来反映其性质。虽然上述方法建立的模型均基本能够反映黄土的流变特征，但多数模型结构较为复杂，涉及的参数众多，这不利于黄土工程建设的推广。殷德顺等[5]提出了一种软体元件，应用分数阶微积分的原理描述介于理想固体与流体之间的岩土材料流变特性。该模型不仅能描述黄土的非线性衰减蠕变和等速蠕变，而且其结构简单，涉及参数少，具有很好的推广意义。除此之外，一些学者[6-17]在对其他岩土材料进行蠕变模型研究时，引入了损伤力学及其他非线性建模技术，这给研究黄土蠕变模型积累了一定的技术经验。

本文则在上述研究的基础上，结合软体元件与线性力学元件，并引入考虑含水损伤的变量，尝试建立一个参数少，又能反映黄土整体蠕变的非线性含水损伤蠕变模型。

2 不同含水率Q2黄土三轴蠕变试验

2.1 试验材料及方法

试样取自陕西省咸阳市礼泉县某黄土崩塌坡脚处天然Q2黄土。土样多呈黄褐色，垂直节理发育、土质密实均匀、天然含水量低。野外选取的试样经室内加工后尺寸均为ø39.1 mm×80 mm的圆柱体。按照试验目的，采用水膜迁移法对其他试样进行人工增湿。得到4种不同含水率(8%，13%，17%，23%)的Q2黄土试样。

蠕变试验所用的仪器为CSS-2901TS型土体三轴流变试验机。试验采用分级加载的方式进行，围压恒定在50 kPa。试验前应用常规三轴固结不排水试验得出不同含水率试样的破坏强度，预先规定蠕变试验的加载级数N，然后确定每级加载的荷载增量。试验时每一级加载持续12 h，待试样变形稳定后，再加下一级荷载。

2.2 含水Q2黄土蠕变特性

利用Boltzmann叠加原理对蠕变试验结果进行分析整理，得到各不同含水率Q2黄土试样在50 kPa围压下的各级轴向荷载的应变-时间曲线(图1)。

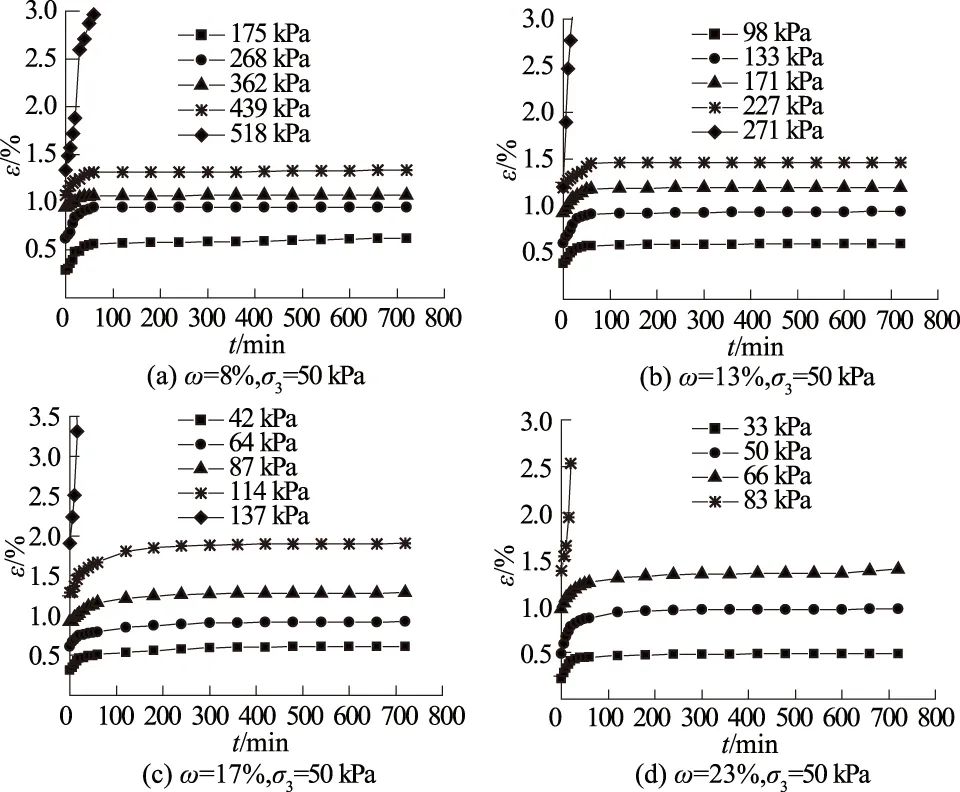
图1 不同含水率Q2黄土三轴蠕变试验曲线Fig.1 Strain-time curves of triaxial creep tests on Q2 loess of different moisture contents

图1中：ε为轴向变形；t为蠕变时间；ω为含水率；σ3为围压。由图1观察分析可知，不同含水率的Q2黄土蠕变具有如下特征：

(1) 不同含水率的黄土蠕变均能观察到初始减速蠕变、等速蠕变和加速蠕变阶段。

(2) 加载瞬时，不同含水率的黄土试样均出现瞬时变形，且瞬时变形会随着加载水平的增加而增大。

(3) 当围压水平一定时，蠕变变形受含水量影响显著，随着含水率的增大，同级加载下的应变量也随之增加。

(4) 当加载的应力水平低于某一临界时，黄土蠕变呈现衰减稳定，且达到稳定时间较短，随后蠕变以接近0的恒定速率继续发展。

(5) 当加载应力水平高于某一临界值时，黄土均会出现加速蠕变，而且随着含水率的增大，加速蠕变从出现到试样破坏时间减小。

(6) 随着含水率的增大，黄土出现加速蠕变所需要的临界应力也逐渐减小。

3 非线性蠕变模型

3.1 分数阶微积分的软体元件

传统的岩土材料流变模型是由虎克体、牛顿体及理想塑性体经过不同的串并联组合构成。虎克体为一弹簧元件，主要用以描述材料的纯弹性特征；牛顿体为一阻尼器元件，主要用以描述材料的黏滞性。从数学角度出发，弹簧元件的本构关系满足虎克定律：σ(t)- d0ε(t)/dt0；黏滞元件的本构关系满足Newton定律：σ(t)-d1ε(t)/dt1。含分数微积分的软体元件(σ(t)-dβε(t)/dtβ)被认为是介于理想固体和理想流体之间的一种元件模型(图2)，能够很好地反映岩土材料的黏弹性特征。

图2 软体元件Fig.2 Soft-matter element

图2中：ξ为软体元件黏弹性系数；β为软体元件分数阶微积分表述时的阶数。

目前，关于分数阶微积分有很多定义，本文采用Riemannn-Liouville型分数阶微积分算子理论，对于函数f(t)的β阶积分定义为

(1)

对分数阶微分则定义为

(2)

式中：β>0，且n-1<β≤n(n为正整数)；Γ(β)为Gamma函数，其定义为

(3)

分数阶微积分的拉氏变换公式为

(4)

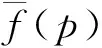
软体元件的本构方程为

σ(t)=ξdβε(t)/dtβ,(0≤β≤1) 。

(5)

当β=1时，软体元件即转化为阻尼器元件，代表理想流体；当β=0时，软体元件则变为弹簧元件，代表理想固体；而当β介于(0， 1)时，该软体元件就表示为介于理想固体与理想流体之间的岩土材料。ξ为黏弹性系数，其物理量纲为[应力·时间β]。

当σ(t)=const时，软体元件即描述岩土材料的蠕变行为，对式(5)两边进行积分，依据Riemannn-Liouville型分数阶微积分算子理论，可得到软体元件的蠕变方程为

(6)

对于不同材料， 调整方程中的参数ξ和β， 即可达到改变蠕变曲线旋转程度， 更加准确反映材料的蠕变特性。 根据文献[7]的研究成果， 当0<β<1时， 软体元件描述的是介于理想固体与理想流体之间的岩土材料流变行为； 当β>1时， 式(6)的曲线为上凹形的应变随时间加速增长曲线， 单论曲线的形态是可以描述材料蠕变曲线的加速蠕变阶段。

3.2 非线性蠕变模型

根据含水Q2黄土三轴蠕变试验结果显示，黄土的变形包括2个部分：一为瞬时变形；另一为蠕变变形。对于黄土的瞬时变形通常可用一弹簧来描述，而对于黄土的蠕变变形，当加载应力小于黄土的屈服应力时，蠕变变形主要出现减速蠕变与等速蠕变；当加载应力大于黄土的屈服应力时，黄土蠕变曲线出现时间短暂的加速蠕变；介于其曲线形态所表现的特点，本文尝试用软体元件来描述黄土的蠕变变形特征。为全面描述Q2黄土的流变特性，我们基于分数阶微积分特点，采用文献[7]提出的四元件蠕变模型(图3)。

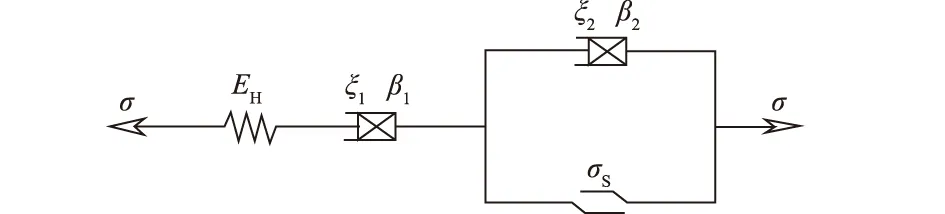
图3 黄土非线性蠕变模型Fig.3 Nonlinear creep model of loess

由图3的模型结构及连接特性可得到模型的蠕变方程为

(7)

(8)

对上式中D(·)采用Riemannn-Liouville型分数阶微积分算子，可得到黄土非线性蠕变方程为

当σ<σs时，

(9)

当σ≥σs时，

0<β1<1，β2>1 。

(10)

式中：EH为瞬时弹性模量；ξ1和ξ2为黏弹性系数；β1,β2为分数阶微积分阶数。

3.3 参数辨识

采用上述基于分数阶微积分构造的黄土非线性蠕变模型，应用1stOpt数学软件基于Levenberg-Marquardt优化算法，对前述Q2黄土三轴蠕变试验数据进行回归分析拟合求参。表1为不同含水率下黄土试样在不同加载应力下的蠕变模型参数。其中EH，ξ1，ξ2为反映黄土材料本身的物理参数，β1与β2为调整曲线形态参数。

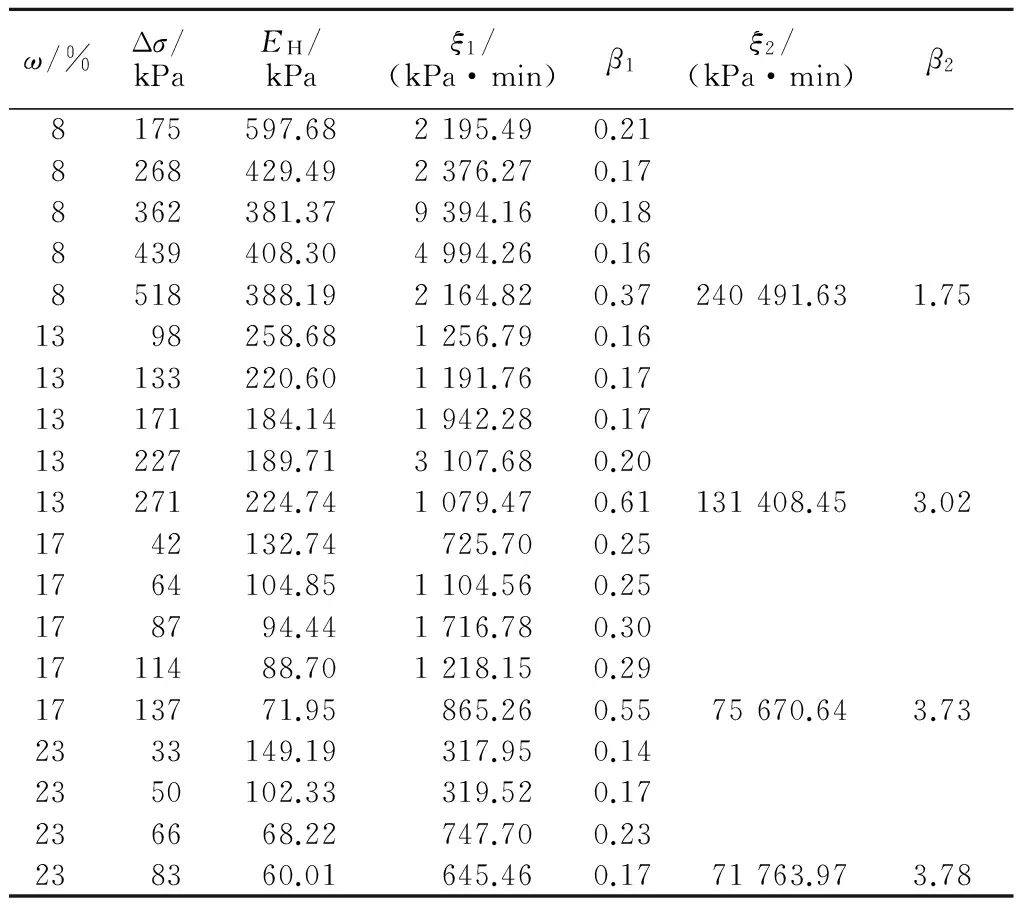
表1 不同含水率非线性蠕变模型参数Table 1 Parameters of nonlinear creep model of loess of different moisture contents

4 非线性含水损伤蠕变模型

4.1 蠕变参数与含水率的关系

为探索水对Q2黄土蠕变特性的影响，在不考虑蠕变参数随应力及时间的变化情况下，分析蠕变参数随含水率的变化规律。首先统计不同含水率下黄土蠕变参数值，继而应用经验法对蠕变参数随含水率变化的数据进行回归分析，拟合出蠕变参数随含水率的变化方程。表2为经统计整理的不同含水率下蠕变参数平均值。

表2 不同含水率蠕变参数均值Table 2 Mean values of creep parameters of loess of different moisture contents

图4是根据表2得到的瞬时变形模量EH、黏弹性系数ξ1随含水率变化的拟合曲线，拟合方程如下式

(11)

由各蠕变参数随含水率关系图及其数学拟合结果分析，各蠕变参数数值均随着含水率的增加呈指数形式y=αexp(-βx)递减。其中ξ1变化最为显著，其次为EH。各蠕变参数随含水率的变化说明了水体对黄土力学性质的弱化和劣化。在黄土受荷时，由于水的作用，导致黄土材料损伤效应更加严重，流变性能增强。

4.2 损伤变量及其演化方程

损伤力学指出，材料在加载过程中由于裂纹的不断连接、扩展壮大，致使材料抵御变形和破坏的能力逐渐降低。而黄土材料在水体作用下，力学性质被弱化和劣化得更加明显，导致其力学参数值随含水率增高而逐渐降低。对于黄土材料，初始状态时，试样体内本身存在孔隙或空隙缺陷，因此，在应力加载下即使产生损伤，在不同含水率下，其损伤程度加剧不同。

根据能量损伤的定义、含水黄土蠕变特点及前节蠕变参数随含水率变化关系的研究结果，本文定义考虑含水损伤的变量为

(12)

式中：F(ω)为任意含水状态下蠕变参数值，即F(ω)=EF(ω)或F(ω)=ξ1(ω)；F(0)为干燥状态时的蠕变参数值。干燥状态损伤为0，随着含水率的增加，损伤变量D(ω)越来越大，但其量值始终小于1。利用式(12)可以计算出不同含水状态下反映不同蠕变参数劣化的Q2黄土损伤量值，即可得出不同含水率与损伤量值之间的关系数据。采用最小二乘法对其数据进行拟合，终可得到不同蠕变参数的损伤变量演化方程，即

(13)

参数EH与ξ1的损伤与含水率ω拟合曲线如图5所示。由图5知，各蠕变参数下的损伤随着含水率的增大而增大。当含水率达到30%左右时，各蠕变参数的损伤接近于1，临近溶解破坏。

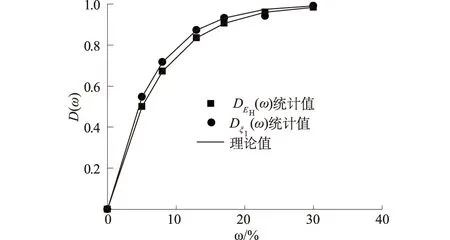
图5 DEH(ω)与Dξ1(ω)随含水率的拟合曲线Fig.5 Fitted curves of DEH(ω) and Dξ1(ω)vs. moisture content

4.3 考虑含水损伤的非线性蠕变模型

基于损伤力学的应变等效性原理，以前述建立的Q2黄土非线性蠕变模型为基础，建立考虑含水参数损伤的Q2黄土非线性蠕变模型。对于一维蠕变问题，将各蠕变参数的含水损伤演化方程代入式(9)与式(10)，可得Q2黄土含水损伤蠕变本构方程。

当σ<σs时,

(14)

当σ≥σs时,

(15)

4.4 模型验证

为验证本文建立的Q2黄土含水损伤蠕变模型的正确性及准确性，再次应用1stOpt数学软件对前述含水率8%的Q2黄土三轴蠕变试验数据进行回归分析拟合求参。求取的参数如表3所示，图6为模型理论值与试验值的对比曲线。由图6可观察出，考虑含水损伤的非线性蠕变模型在描述Q2黄土流变特性时，其精确效果较高。

表3 含水率8%黄土损伤蠕变模型参数Table 3 Parameters of damage creep model (moisture content 8%)

图6 含水率8%试样蠕变试验值与理论值Fig.6 Test values and theoretic values of creep of loess specimen (moisture content 8%)

5 结 论

(1) 不同含水率Q2黄土三轴蠕变试验结果显示，含水率的增高伴随着黄土流变性能的增强。

(2) 由蠕变试验数据进行回归分析得出的非线性蠕变模型参数值随含水率的增加呈现指数型递减的规律，此现象充分说明了水对黄土具有较强的力学劣化影响。

(3) 依据能量损伤建立的考虑含水因素的损伤变量及其演化方程，可有效描述不同含水量对黄土的损伤劣化效果。

(4) 应用损伤力学的应变等效原理，将各损伤演化方程代入分数阶微积分蠕变模型，得到考虑含水损伤的非线性蠕变方程，该方程经过验证，可有效描述Q2黄土瞬时变形、衰减蠕变、等速蠕变和加速蠕变。

[1] 郭增玉,张朝鹏,夏旺民.高湿度Q2黄土的非线性流变本构模型及参数[J].岩石力学与工程学报,2000,19(6):780-784. (GUO Zeng-yu, ZHANG Chao-peng, XIA Wang-min. Nonlinear Rheological Constitutive Models and Their Parameters of High Moisture Q2Loess[J]. Chinese Journal of Rock Mechanics and Engineering, 2000,19(6):780-784. (in Chinese))

[2] 朱才辉,李 宁,刘俊平.压实Q3马兰黄土蠕变规律研究[J].西安理工大学学报,2011,27(4):392-399. (ZHU Cai-hui, LI Ning, LIU Jun-ping. Research on the Creep Behavior of Compacted Q3Malan Loess[J]. Journal of Xi’an University of Technology, 2011,27(4):392-399.(in Chinese))

[3] 谢 星,王东红,赵法锁.Q2黄土流变特性及其统计损伤流变模型[J].水文地质工程地质,2010,37(3):63-68. (XIE Xing, WANG Dong-hong, ZHAO Fa-suo. Study on Rheological Properties and Statistical Damage Rheological Model for Q2Loess[J]. Hydrogeology & Engineering Geology, 2010,37(3):63-68.(in Chinese))

[4] 王东红,谢 星,赵法锁.考虑蠕变损伤的Q2黄土流变本构模型[J].西安科技大学学报,2010,30(6):682-686.(WANG Dong-hong, XIE Xing, ZHAO Fa-suo. Creep Damage Rheological Constitutional Model for Q2Loess[J]. Journal of Xi’an University of Science and Technology, 2010, 30(6): 682-686. (in Chinese))

[5] 殷德顺,任俊娟,和成亮,等.一种新的岩土流变模型元件[J].岩石力学与工程学报,2007,26(9):1989-1903. (YING De-shun, REN Jun-juan, HE Cheng-liang,etal. A New Rheological Model Element for Geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 2007,26(9):1989-1903. (in Chinese))

[6] 张永兴,王更峰,周小平,等. 含水炭质板岩非线性蠕变损伤模型及其应用[J].土木建筑与环境工程,2012,34(3):1-9. (ZHANG Yong-xing, WANG Geng-feng, ZHOU Xiao-ping,etal. Nonlinear Creep Damage Model of Water Bearing Carbonaceous Slate and Its Application[J]. Journal of Civil, Architectural & Environmental Engineering, 2012, 34(3): 1-9. (in Chinese))

[7] 陈 亮,陈寿根,张 恒，等.基于分数阶微积分的非线性黏弹塑性蠕变模型[J].四川大学学报(工程科学版),2013,45(3):7-11.(CHEN Liang, CHEN Shou-gen, ZHANG Heng,etal. A Nonlinear Viscoelasto-plastic Creep Model Based on Fractional Calculus[J]. Journal of Sichuan University (Engineering Science Edition), 2013,45(3):7-11. (in Chinese))

[8] 王者超,乔丽苹.土蠕变性质及其模型研究综述与讨论[J].岩土力学,2011,32(8):2251-2260. (WANG Zhe-chao, QIAO Li-ping. A Review and Discussion on Creep Behavior of Soil and Its Models[J]. Rock and Soil Mechanics, 2011,32(8): 2251-2260. (in Chinese))

[9] 宋勇军,雷胜友,韩铁林.一种新的岩石非线性黏弹塑性流变模型[J].岩土力学,2012,33(7):2076-2080. (SONG Yong-jun, LEI Sheng-you, HAN Tie-lin. A New Nonlinear Viscoelasto-plastic Rheological Model for Rocks[J]. Rock and Soil Mechanics, 2012,33(7):2076-2080. (in Chinese))

[10]宋勇军,雷胜友.基于分数阶微积分的岩石非线性蠕变损伤力学模型[J].地下空间与工程学报,2013,9(1):91-95. (SONG Yong-jun, LEI Sheng-you. Mechanical Model of Rock Nonlinear Creep Damage Based on Fractional Calculus[J]. Chinese Journal of Underground Space and Engineering, 2013,9(1):91-95.(in Chinese))

[11]谢 星,赵法锁,王东红.西安地区Q2黄土非线性流变特性[J].长安大学学报(自然科学版),2009,29(5):41-46. (XIE Xing, ZHAO Fa-suo, WANG Dong-hong. Nonlinear Rheological Model for Q2Loess in Xi’an Region[J].Journal of Chang’an University (Natural Science), 2009,29(5):41-46.(in Chinese))

[12]赵宪民,段 钊,何青峰,等.延安Q2黄土三轴蠕变特性试验研究[J].长江科学院院报,2012,29(11):77-81. (ZHAO Xian-min, DUAN Zhao, HE Qing-feng,etal. Triaxial Test on the Creep Characteristics of Q2Loess in Yan’an[J]. Journal of Yangtze River Scientific Research Institute, 2012,29(11):77-81.(in Chinese))

[13]王松鹤,骆亚生,董晓宏,等.黄土剪切蠕变特性试验研究[J].岩石力学与工程学报,2010,29(增1):3088-3092. (WANG Song-he, LUO Ya-sheng, DONG Xiao-hong,etal. Experimental Study of Shear Creep Characteristics of Loess[J]. Chinese Journal of Rock Mechanics and Engineering, 2010,29(Sup.1):3088-3092.(in Chinese))

[14]刘桃根, 王 伟, 吴斌华,等.基于损伤力学的砂岩蠕变模型研究与参数辨识[J].三峡大学学报(自然科学版),2010,32(6):55-60. (LIU Tao-gen, WANG Wei, WU Bin-hua,etal. Sandstone Creep Model Study and Parameter Identification Based on Damage Mechanics[J]. Journal of China Three Gorges University(Natural Sciences), 2010,32(6):55-60. (in Chinese))

[15]曹文贵, 袁靖周, 王江营,等. 考虑加速蠕变的岩石蠕变过程损伤模拟方法[J].湖南大学学报(自然科学版),2013,40(2): 15-20. (CAO Wen-gui, YUAN Jing-zhou, WANG Jiang-ying,etal. A Damage Simulation Technique of the Full Rock Creep Process Considering Accelerated Creep[J]. Journal of Hunan University (Natural Sciences), 2013,40(2): 15-20. (in Chinese))

[16]梁小勇, 薛晓辉, 王虎妹,等. 岩石时间硬化损伤蠕变特性[J].辽宁工程技术大学学报(自然科学版),2013,32(4):509-512.(LIANG Xiao-yong, XUE Xiao-hui, WANG Hu-mei,etal. Damage Creep Characteristics of Rock Time-hardening[J]. Journal of Liaoning Technical University (Natural Science), 2013,32(4):509-512.(in Chinese))

[17]林 斌, 赵法锁, 霍 亮. 黄土损伤与流变耦合模型及参数研究[J].工程地质学报,2010,18(5):685-691. (LIN Bin, ZHAO Fa-suo, HUO Liang. Coupling Study on Damage and Rheological Model of Loess and Its Parameter[J]. Journal of Engineering Geology, 2010, 18(5): 685-691. (in Chinese))

(编辑：姜小兰)

Creep Damage Model of Q2Loess in Consideration ofMoisture Content Based on Fractional Calculus

TANG Hao1,3, DUAN Zhao2, ZHAO Fa-suo3, SONG Fei3, LI Xiang-ning3

(1.State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059,China; 2.School of Geology and Environment, Xi’an University of Science and Technology, Xi’an 710054, China; 3.College of Geology Engineering and Surveying Engineering,Chang’an University, Xi’an 710054,China)

Triaxial creep tests on Q2loess of different moisture contents were carried out to explore the creep properties of water-containing Q2loess. Test results show that the rheological property of Q2loess strengthens with the increase of moisture content. Furthermore, since the soft-matter element built by fractional calculus could simulate the material between ideal solid and ideal fluid, a four-element nonlinear creep model which contains the soft-matter element was applied to fit data, and the model parameters under different moisture contents were analyzed. The results suggest that instantaneous deformation modulusEHand viscoelastic coefficientξ1have a negative relationship with moisture content with an exponential decline. A water damage evolution equation of each creep parameter was obtained by introducing the water damage variableD(ω), which was further used to establish a nonlinear creep model in consideration of water damage effect. The nonlinear creep model was verified by test data. It was proved that the nonlinear creep model considering water damage could effectively characterize the overall rheological property of Q2loess，and has a good application prospect.

Q2loess; creep test; moisture content; nonlinear; damage; creep model

2014-02-24；

2014-03-25

中央高校基本科研业务费专项资助项目(CHD2010JC118)

唐 皓(1985-)，男，陕西勉县人，博士后，主要从事地质灾害防治与岩土流变研究，(电话)18615783673(电子信箱)329689614@qq.com。

10.3969/j.issn.1001-5485.2015.08.014

TU432

A

1001-5485(2015)08-0078-06

2015,32(08):78-83