大体积混凝土温控通水参数优选数学模型
朱优平,李同春,冯树荣,石青春,苏军安
(1.中国电建集团 中南勘测设计研究院有限公司, 长沙 410014; 2.河海大学 水利水电学院, 南京 210098)
大体积混凝土温控通水参数优选数学模型
朱优平1,2,李同春2,冯树荣1,石青春1,苏军安1
(1.中国电建集团 中南勘测设计研究院有限公司, 长沙 410014; 2.河海大学 水利水电学院, 南京 210098)
在满足工程要求的前提下,优选温控参数,可以大幅度提高工程效益,节约社会资源,但是目前没有通用性强的大体积混凝土温控参数优选数学模型,温控参数还只能凭经验设计选取,以致温控方案的选取并非是相对造价最低的最优方案,因而不利于控制工程建设成本。鉴于此,对大体积混凝土温控参数优选数学模型进行研究,首次推导出了考虑水管间距、冷却水温沿程变化和流量等影响的无热源和有热源混凝土平均温度计算公式,进而提出了以大体积混凝土温控措施总费用为目标函数,以破坏强度准则为约束方程的温控参数优选数学模型,并编制了求解该模型的遗传算法程序。实例计算表明:该模型简捷、高效,计算结果合理,可为工程的温控设计提供参考。同时,模型的通用性和实用性都较强,便于在工程中运用。
大体积混凝土;温控措施;数学模型;遗传算法;冷却水管
1 研究背景
对大体积混凝土结构进行温度控制,已有几十年的历史。温度控制涉及多个学科知识,其主要措施有表面喷雾、流水养护、预冷骨料和冷却通水等。在满足工程需要的前提下,可供选择的温控方案有很多,其产生的温控费用是不一样的,在大体积混凝土结构中该问题尤为突出,因浇筑方量很大,优选混凝土温控参数,可以显著降低工程成本,节约社会资源。国内外许多学者对大体积混凝土温控参数优选进行了深入的研究。丁宝瑛等[1]将非线性规划理论应用到温控优化设计中,采用网格法和复形法对如何选择混凝土浇筑块基础温差这一问题进行了深入研究。后来,王正中[2]在其研究的基础上,通过对温度仿真计算结果的回归分析,拟合出了均匀温差应力系数和非均匀温差的应力的经验公式,以强度控制标准为约束条件对控制混凝土基础温差的温控措施进行了优化。李荣湘等[3]提出了适用于在温控优化中求解温度场的分解迭加法,将实际温度场划分为一系列平均温度场,然后逐个进行降温计算。任智中[4]在不同部位的混凝土浇筑块采用不同的温度控制标准,对浇筑块尺寸、浇筑间歇时间、保温板厚度等因素进行了优化。文献[5]通过大量的数值仿真计算,对具体工程中的各种温控措施进行了系统的研究,得出了一批很有价值的成果。E.M.R.Fairbairn等[6]采用遗传算法对大体积混凝土的温度控制进行了优化。过去的研究都是在特定工程下优选温控参数,不便于推广到其他工程中应用,因此,工程中设计出的温控方案,并不是以相对造价最低为原则设计出来的,而是单纯以经验设计的可行性方案,不利于控制工程建设成本。本文所提出的温控参数优选数学模型,不仅能够快速设计出最优温控方案,而且可以应用到任何工程中,通用性强。为了建立温控参数优选数学模型,考虑水管间距、冷却水温沿程变化和流量等对混凝土平均温度的影响,首次推导出了在通水冷却条件下无热源和有热源混凝土平均温度的2个计算公式,然后以温控措施的总费用最低作为优选目标,以混凝土的破坏强度准则为约束方程,建立了大体积混凝土温控参数优选数学模型。模型的求解是一个非线性优化问题,方法有很多种,本文在算例中选用效率较高的遗传算法进行求解,通过自编程序计算表明,该方法简捷、高效,计算结果合理,可以为工程的温控设计提供参考。
2 通水冷却条件下混凝土平均温度的计算
冷却水管中流动的水吸收混凝土中散发出来的热量,以更高的温度从出口流出,从而达到降低混凝土温度的目的。大体积混凝土中冷却水管具有数量大且蛇形弯曲等特点,要严格求出其降温速率是极其困难或者可以说是不现实的。虽然现有的数值计算能够较精确地模拟出冷却水管的效果,但是每个工程的水管布置形式、水管间距、通水流量、通水温度、混凝土浇筑温度等一般都不同,在确定混凝土降温速率与边界条件和初始条件的函数关系时,需要设计大量的工况进行仿真,从计算结果中拟合出其函数关系,这样做不仅严重浪费了计算机资源,而且其结果的可信度也还有待进一步考究。
美国恳务局和我国朱伯芳院士都曾就含冷却水管混凝土温度计算进行了深入研究,分别采用分离变量法和拉普拉斯变换法求解了极坐标下混凝土柱体的热传导问题,得到了混凝土平均温度的级数解,近似取第一项得
(1)
式中a1b为特征方程的第一根,当b/c=100时,a1b=0.716 7,在b/c≠100时,需要查阅已经制作好的数学表格,这在工程应用中不便。为此,本文从极坐标下热传导方程入手,建立了混凝土降温速率和浇筑温度及冷却通水之间的关系。
2.1 无热源混凝土平均温度计算方法
冷却水管的管壁很薄,在任何时候,管壁内都可以认为是平面稳定温度场[7-8]。建立管壁处的极坐标热传导方程,即
(2)
边界条件:r=c时,
T=Tw;
(3)
r=b时,
T=Tc。
(4)
式中:b,c分别为水管的外半径和内半径;Tw为水管内的水温;Tc为混凝土的温度。
求解式(2)至式(4)得到管壁内的温度为
(5)
根据文献[9-10]的推导,简化后的水管水温沿程变化应满足:
(6)
式中:cw,ρw,qw分别为冷却水的质量热容、密度和流量;λp为水管的导热系数;Δl为水管的沿程长度;Γp为混凝土与冷却水管的交界面。将式(5)代入式(6)得
(7)
式(7)可以改写成一个普通的一阶偏微分方程,即
解方程式(7)得
Tw(l)=(Tcekl-Tc+Tw0)e-kl。
(8)
其中,
(9)
式中Tw0为冷却水管的进口水温。运用式(8)可求出冷却水管中出口水温,那么冷却水管在dt时间段内带走的热量为
Q1=cwρwqw(Tw(l)-Tw0)dt。
(10)
在温度控制中,我们更加关心的是混凝土断面的平均温度,混凝土中的冷却水管一般为矩形布置,其水平间距为S1,铅直间距为S2,因此,可以认为每根水管的平均冷却面积为S1×S2。混凝土的热量通过冷却水管中水带走,混凝土温度降低,在dt时间段内混凝土损失的热量为
(11)
由热量守恒定律,水体带走的热量应等于混凝土损失的热量,注意到正负号,则有
Q1=-Q2,
(12)
即
(13)
此式也是一个一阶常微分方程,解得

(14)
其中,
(15)
2.2 有热源混凝土平均温度计算方法
上节主要讨论了无热源混凝土平均温度的计算问题,在混凝土后期由于水化热基本已散发完毕,因此,运用上节的公式计算混凝土的平均温度是合理的,但是在水化反应剧烈的施工期就不能运用上节的公式进行计算,下面主要讨论有热源时混凝土平均温度的计算问题。
在考虑水化反应时,混凝土中的热量可以分解为3个部分,混凝土损失的热量、冷却水导出的热量和水化反应放出的热量。这3部分热量存在以下的关系式,即
Q1=-Q2+Q3,
(16)
式中Q3为混凝土在单位时间内放出的热量。最后得到一个基本的一阶常微分方程
(17)
式中θ为混凝土的绝热温升,一般有3种表达式。解式(17)得

(18)
由式(14)和式(18)分别可以计算通水条件下无热源和有热源混凝土在任意时刻的平均温度,从公式中可以看出,该公式能够体现浇筑温度、水管间距、冷却水温和冷却水流量对混凝土平均温度的影响,其中的冷却水温考虑其在水管中的沿程变化。在其后建立的温控参数优选数学模型的约束方程中,这2个公式将起到重要的作用。
3 温控参数优选数学模型
3.1 目标函数
在大体积混凝土施工过程中,有许多种温控措施可供选择[11-12]。本文以温控措施的总费用F最低作为优选目标,较预冷骨料、冷却通水而言,表面喷雾和流水养护等其他措施对降低混凝土内部温度的效果要小得多,因此,只考虑浇筑温度和通水冷却等有关的参数变化对混凝土温控费用的影响,目标函数表达式为
minF=[k1S1S2l(Ta-Tc0+
k2qwt(Ta-Tw0)]/S1S2l。
(19)
式中:F为1 m3混凝土的温控费用;k1是使得1 m3混凝土降低1℃所需的费用;l为冷却水管长度;Ta为气温;Tc0为混凝土的浇筑温度;k2是使得1 m3水降低1℃所需的费用;qw为冷却通水流量;t为冷却通水时间。
3.2 约束方程
混凝土中产生裂缝的根本原因是拉应力超过了混凝土的抗拉极限,如果水泥品种和基岩特性等条件已经确定,控制混凝土的温差ΔT,就可以有效地减少混凝土产生的温度应力,对混凝土的防裂是极其有利。按照强度破坏准则,混凝土不产生的裂缝的条件为[13]
σT[σ] 。
(20)
式中 [σ]为混凝土的抗拉强度,在实际工程中,出于对结构安全性能的考虑,一般要把安全系数引入到计算中去,则将式(20)改写为
σT[σ]/K。
(21)
式中K为安全系数,常取值在1.1~1.5之间,其具体取值要考虑工程结构的重要性。
考虑自身体积变形和徐变后,内部混凝土温度应力可以近似表示为
(22)
式中:ΔT为混凝土的降温量;α为混凝土的线膨胀系数;E为混凝的弹性模量;R为基岩或老混凝土对新混凝土的约束系数,其值随混凝土尺寸、材料性质和基岩刚度变化的;Kp为混凝土的徐变松弛系数;μ为混凝土的泊松比;εg为混凝土的自身体积变形。
将式(22)代入式(21)得到防止出现温度裂缝的条件,即
ΔT
(23)
在大体积混凝土内部,式(23)中的ΔT即为混凝土的基础温差:
ΔT=maxTc-Tf。
(24)
式中:maxTc为混凝土的最高温度,即式(14)和式(18)中Tc的最大值;Tf为混凝土的稳定温度,一般为多年气温平均值。
4 模型求解及程序设计
由式(19)和式(23)构成的大体积混凝土温控参数优选数学模型是一个非线性优化问题,其求解方法繁多,其中遗传算法作为一种全局优化搜索算法,为解决最优化问题提供了一个有效的途径和通用框架[10]。本文的求解方法采用遗传算法,当然也可以采用其他求解方法。依据式(14)或式(18)、式(19)和式(23),采用遗传算法并应用Fortran语言编制程序进行求解,遗传算法的基本原理及程序设计可参考文献[14-15],模型求解具体步骤如下:
(1) 按照当地物价估算出, 1 m3混凝土预冷1℃所需的费用和1 m3水冷却1℃时所需的费用。
(2) 设定浇筑温度、通水时间、冷却水温和水管间距的取值范围。
(3) 生成初始种群。
(4) 利用式(14)或式(18)计算出通水结束时混凝土的平均温度,通水结束后继续考虑混凝土水化热引起的温升量。利用式(19)计算温控费用,检查其基础温差ΔT是否满足式(23),如果不满足则给该组合下的温控费用赋一个大值。
(5) 构造适应度函数,本文依据温控费用,采用基于序的适应度函数,并进行遗传算法里面的复制、选择和变异操作。
(6) 重复第(4)步和第(5)步,直到收敛。
5 算 例
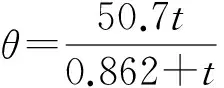
其对应的数学模型为
(25)
式(18)中的积分采用6阶Newton-Cotes积分公式计算。遗传算法进行求解时,浇筑温度的取值范围Tc0∈[10,30],水管入口水温Tw0∈[10,30],通水时间t∈[0,30],S1×S2∈[1,9],种群数量为100,迭代100步。
计算结果为,当Tc0=28.64,Tw0=26.63,t=5.49,S1×S2=6.17=2.48×2时,得到F的最小值minF=7.93。
因此,在本例中,要使得混凝土不出现裂缝,每m3混凝土至少应花费7.93元的温控费用。在该例中,如果未经温控参数优化,凭经验取Tc0=25,Tw0=20,t=10,S1×S2=2.25=1.5×1.5,则每m3混凝土需花费79.7元的温控费用,大大超过了优选后的温控费用。大坝的混凝土浇筑方量都在几百万立方以上,因此,对工程中的温控参数进行优选能节省几千万甚至上亿元的温控费用,经济效益显著。
6 结 语
为了防止产生裂缝,大体积混凝土要进行温度控制,已经在工程界形成了共识,但是长期以来,由于缺少一个通用性强的大体积混凝土温控参数优选数学模型,温控方案大多是凭科研设计人员的经验制定,具有很强的随意性,并不是温控总费用最低的最优方案,无形中增加了工程的建设成本。本文针对大体积混凝土温控参数优选数学模型进行研究,具体做了如下几方面的工作:
(1) 考虑了水管间距、冷却水温沿程变化和流量等影响因素,首次推导出了通水冷却下无热源和有热源混凝土平均温度的计算公式。
(2) 提出了大体积混凝土温控参数优选数学模型,以温控总费用最低为目标函数,以强度准则为约束条件,该模型表述简捷,计算高效,通用性强,便于在工程中推广应用。
(3) 通过遗传算法,求解该模型并用其优化某一大坝的温控参数,结果表明,优化后的温控费用显著降低,有利于控制工程的建设成本。
[1] 丁宝瑛,王国秉,谢良安,等.混凝土坝温度控制设计的优化[J].水利学报,1982,(1):12-19. (DING Bao-ying, WANG Guo-bing, XIE Liang-an,etal. The Optimum Design of Temperature Control for Mass Concrete Dams[J]. Journal of Hydraulic Engineering, 1982, (1):12-19. (in Chinese))
[2] 王正中.大体积混凝土浇筑块的温度控制[J].陕西水力发电,1989,(7):16-23. (WANG Zheng-zhong. Temperature Control of Mass Concrete Block[J]. Journal of Shaanxi Water Power, 1989,(7):16-23. (in Chinese))
[3] 李荣湘,强茂山.混凝土坝整体温度控制措施优化设计[J].清华大学学报,1989,29(2):79-85. (LI Rong-xiang, QIANG Mao-shan. Optimization Design of Temperature Control Measures Used in Whole Dams[J]. Journal of Tsinghua University, 1989,29(2):79-85. (in Chinese))
[4] 任智中.大坝混凝土温度控制措施的的整体优化[J].水利水电技术,1990,(6):47-51. (REN Zhi-zhong. Temperature Control Measures of Dam Concrete Optimized Overall[J]. Water Resources and Hydropower Engineering, 1990, (6): 47-51. (in Chinese))
[5] 张宇鑫,黄达海,刘德福.高拱坝混凝土温度控制优化设计研究[J].水利水电技术,2003,34(4):25-29. (ZHANG Yu-xin, HUANG Da-hai, LIU De-fu. Study on Concrete Thermal Optimum Design of High Arch Dams[J]. Water Resources and Hydropower Engineering, 2003, 34(4): 25-29. (in Chinese)) [6] FAIRBAIRN E M R, SILVOSO M M, FILHO R D T,etal. Optimization of Mass Concrete Construction Using Genetic Algorithms[J].Computers & Structures, 2004,82(2/3): 281-299.
[7] 朱伯芳.大体积混凝土非金属水管冷却效果的降温计算[J].水力发电,1996,(12):26-29. (ZHU Bo-fang. Temperature Drop Calculation of Mass Concrete Cooled by Non-metal Pipeline[J]. Water Power,1996, (12): 26-29. (in Chinese))
[8] 朱伯芳.考虑水管冷却效果的混凝土等效热传导方程[J].水利学报,1991,(3):28-34. (ZHU Bo-fang. Equivalent of Heat Conduction in Mass Concrete Considering the Effect of Pipe Cooling[J]. Journal of Hydraulic Engineering, 1991, (3): 28-34. (in Chinese))
[9] 朱伯芳,蔡建波.混凝土坝水管冷却效果的有限元分析[J].水利学报,1985, (4):27-36. (ZHU Bo-fang, CAI Jian-bo. Finite Element Analysis of the Effect of Pipe Cooling in Concrete Dams[J]. Journal of Hydraulic Engineering, 1985, (4): 27-36. (in Chinese))
[10]朱岳明,徐之青,贺金仁,等. 混凝土水管冷却温度场的计算方法[J] .长江科学院院报,2003,20(2):19-22. (ZHU Yue-ming, XU Zhi-qing, HE Jin-ren,etal. A Calculation Method for Solving Temperature Field of Mass Concrete with Cooling Pipes[J]. Journal of Yangtze River Scientific Research Institute,2003, 20(2):19-22. (in Chinese))
[11]丁宝瑛,王国秉,黄淑萍,等.国内混凝土坝裂缝成因综述与防止措施[J].水利水电技术,1994,(4):12-18. (DING Bao-ying, WANG Guo-bing, HUANG Shu-ping,etal. A Review on Causes of Cracking in Domestic Concrete Dams and Preventive Measures[J]. Water Resources and Hydropower Engineering, 1994,(4):12-18. (in Chinese))
[12]龚召熊,张锡祥,肖汉江,等.水工混凝土的温控与防裂[M].北京:中国水利水电出版社,1999:3-4. (GONG Zhao-xiong, ZHANG Xi-xiang, XIAO Han-jiang,etal. Temperature Control and Crack Prevention of Hydraulic Concrete[M]. Beijing: China Water Power Press, 1999: 3-4.(in Chinese))
[13]朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京:中国电力出版社,1998:548-602. (ZHU Bo-fang. Thermal Stress and Temperature Control of Mass Concrete[M]. Beijing: China Electric Power Press, 1998: 548-602. (in Chinese))
[14]李敏强. 遗传算法的基本理论与应用[M]. 北京:科学出版社, 2002. (LI Min-qiang. The Basic Theory and Application of Genetic Algorithms[M]. Beijing: Science Press, 2002. (in Chinese))
[15]段玉倩. 遗传算法及其改进[J]. 电力系统及其自动化学报, 1998, 10(1): 39-52. (DUAN Yu-qian. Genetic Algorithm and Its Modification[J]. Proceeding of the CSU-EPSA,1998,10(1): 39-52. (in Chinese))
(编辑:陈绍选)
Mathematical Model of Parameter Optimization forthe Temperature Control of Mass Concrete
ZHU You-ping1,2, LI Tong-chun2, FENG Shu-rong1, SHI Qing-chun1, SU Jun-an1
(1.Power China Zhongnan Engineering Corporation Limited, Changsha 410014, China;2.College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China)
Optimizing temperature control measures under the premise of meeting engineering requirements could improve project efficiency and save social resource. But currently a versatile mathematical model of parameter optimization for the temperature control of mass concrete is in lack, and as a result, the temperature control parameters can only be selected according to experience, which is unfavorable to control the construction cost. In view of this, formulas of mass concrete’s average temperature in the presence and in the absence of heat source were respectively deduced considering the effects of cooling pipe distance, variation of water temperature along the pipe, and flow rate. Furthermore, a mathematical model was built and genetic algorithm to solve the model was presented. The model takes the total cost of temperature control measures as objective function and the strength failure criterion as constraint equation. Calculation examples prove that the model is simple, efficient and reasonable. Moreover, it is versatile and feasible to be applied to engineering practice.
mass concrete; temperature control measure; mathematical model; genetic algorithm;water-cooling pipe
2014-03-17;
2014-05-22
国家自然科学基金面上项目(51079044);国家自然科学基金青年项目(51009056)
朱优平(1982-),男,湖南双峰人,博士后,主要从事水工结构研究,(电话) 13808462761(电子信箱)zhuyoupingcs@163.com。
10.3969/j.issn.1001-5485.2015.08.023
TV315
A
1001-5485(2015)08-0126-05
2015,32(08):126-130

