基于正态模糊线性回归确定河流横向扩散系数

张 转，常安定，王媛英，王晓晨

(1.陕西国际商贸学院，陕西 咸阳 712046; 2.长安大学 理学院， 西安 710064)

基于正态模糊线性回归确定河流横向扩散系数

张 转1，常安定2，王媛英2，王晓晨2

(1.陕西国际商贸学院，陕西 咸阳 712046; 2.长安大学 理学院， 西安 710064)

为寻求水质污染时河流扩散参数的计算方法，以确定河流横向扩散系数的直线图解法为基础，在模糊数的基础上分析河流水团示踪试验数据，建立正态模糊线性回归模型，通过模糊集的隶属函数计算不同置信水平下河流横向扩散系数和河流平均流速等河流水质参数的取值区间。实际算例验证结果表明，应用正态模糊线性回归模型确定的河流水质参数值与真值非常接近，说明该方法是可行的，并且是可靠、合理的。该方法能够反映河流系统自身的不确定性以及实际中存在的各种不确定因素对其的影响。

模糊线性回归；正态模糊数；隶属函数；横向扩散系数；平均流速

1 研究背景

近年来地下水遭到不同程度的污染，地下水中溶质运移理论愈来愈引起人们的关注。因此,河流水质问题成为了水环境工作者重点研究的问题之一。在研究河流水质问题时，最重要的是河流扩散参数[1]，它是反映河流综合特征、建立水质模型、对河流水质状态进行预测和预报的基础性参数，其确定的方法有理论公式法、经验公式法和水团示踪试验法。目前，对于分析瞬时投放一定质量的示踪剂条件下的野外一维稳定流场河流的试验数据、确定河流的纵向扩散参数已经建立了数据分析方法，如：单站法、双站法、演算法[2-3]、直线图解法[4]、相关系数极值法[5]以及智能优化算法[6-7]等。而水环境研究者在确定河流的横向扩散参数很少用水团示踪试验法，主要应用经验公式法进行推算，仅文献[8]和[9]提出过野外二维河流水团示踪实验数据的相关系数极值法和直线图解法。在确定河流扩散参数时，上述方法均有自己的优点，但又存在着共同的缺陷，即把地下水系统看作是确定的系统，而实际上地下水是一个复杂、随机不确定的系统。然而由于条件限制以及外界因素的影响，野外试验观测的数据具有一定的模糊性，所以最终的参数难免存在不确定性。本文引用文献[10]的思路,以文献[9]的数据和二维稳态河流水质模型的解析解为基础，将河流横向扩散参数看作正态模糊数，通过模糊线性规划确定横向扩散参数对应的模糊数，应用模糊数学中的隶属函数来确定在不同置信水平下参数的取值。这样更加符合实际的反映参数取值对河流系统的适应程度，参数的取值也更具有灵活性。本文通过分析观测孔的取样数据，根据河流的二维稳定水质模型基本方程的解析表达式，可将其线性化，再将回归系数用正态模糊数表示，建立模糊线性回归模型，利用模糊集的λ截集概念确定横向扩散系数和河流平均流速在一定置信水平λ下的取值范围，为确定河流扩散参数提供一种新的途径。

2 基本原理

在河流某一断面的一侧，连续稳定地投入示踪剂溶液，此示踪剂为不可降解的污染物。投放点为空间坐标系的原点O,河水流动方向为x轴正方向，河流的横向为y轴的正方向。假设示踪剂排入河道后，沿水深方向快速、均匀混合，则河流的二维稳定水质解析模型基本方程[11]为

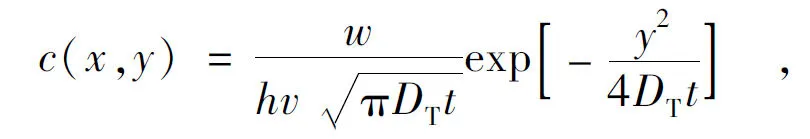
(1)

或者

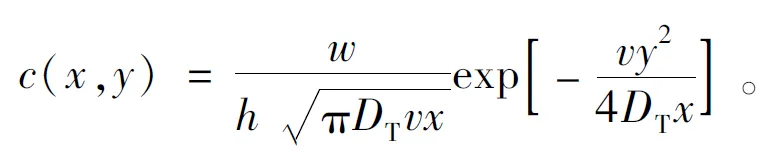
(2)

式中：c(x,y)为河道中(x,y)点处河水中示踪剂的浓度(g/m3)；x为河流的纵向坐标值(m)；y为河流的横向坐标值(m)；h为河道平均水深(m);DT是河流的横向扩散系数(m2/s)；v是河流的平均流速(m/s)；t是时间(s), 以投放示踪剂溶液开始时计时;w为在排放点处投放示踪剂溶液的质量(g/s)，w=c0·q0，其中c0为示踪剂溶液浓度(g/m3)；q0为排放示踪剂溶液的流量(m3/s)。

2.1 同一时刻、同一纵向位置处、沿河流横向不同位置处观测数据分析

此观测试验数据相当于x为定值时，沿y轴不同距离取样，如图1中的点列。式(1)两边同时取自然对数得

(3)

令

Y=lnc,

(4)

X=y2,

(5)

(6)

(7)

则式(3)可变换成如下关系式，即

Y=H1X+H2。

(8)

图1 二维扩散示意图Fig.1 Schematic of two- dimensional diffusion

某河流在水文条件稳定的情况下，河流的横向扩散系数DT、河道平均水深h、河流的平均流速v都是模型参数即为常数，并且在同一时刻，即t为定值。由式(8)可知，自变量X和因变量Y之间存在线性关系。然而由于条件限制以及外界因素的影响，加之河流系统模型本身就具有不确定性，野外试验观测数据也具有一定的模糊性，所以最终的参数即河流的横向扩散系数和河流的平均流速也难免有不确定性。鉴于此，采用模糊线性回归模型来计算河流的平均流速和横向扩散系数。

2.2 基于正态模糊数的模糊线性回归模型

依据一般的线性回归模型，建立模糊线性回归模型如下：

(9)

图2 正态模糊集隶属函数曲线Fig.2 Curve of the membership function of normal fuzzy set

(10)

(1) 各模糊回归系数的模糊程度之和最小，即满足式(1)。

(11)

式中σj(j=1,2,…,n)为各正态模糊系数对应的模糊程度，xij是一组观测数据。

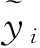
(12)

式中μj(j=1,2,…,n)为各正态模糊数的中心，其他参数同上。

由条件(2)可得

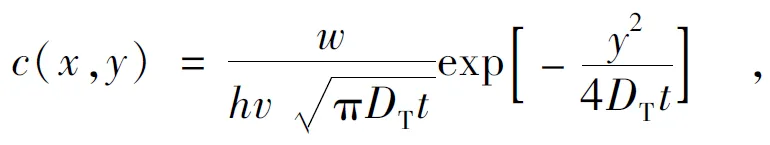
(13)

综上分析得，模糊线性回归模型的最优解可以转化为以下线性规划问题，即

(14)

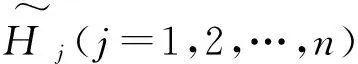
2.3 模糊线性回归模型的应用

应用模糊线性回归模型确定河流的平均流速和横向扩散系数，将式(8)写成下式的模糊线性回归模型,即

(15)

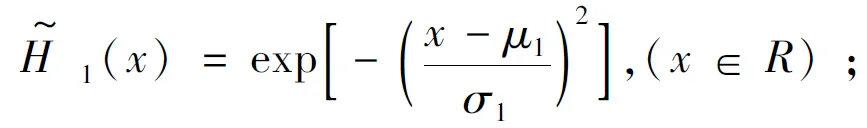
(16)

(17)

根据式(6)和式(16)可得横向扩散系数的隶属函数为

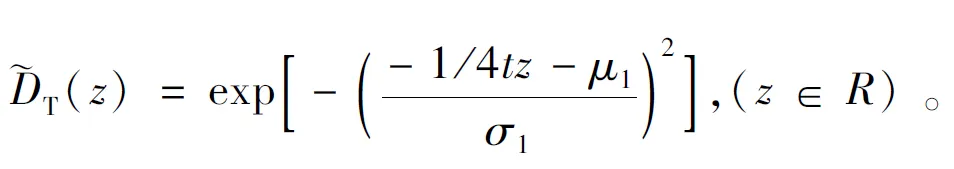
(18)

由式(7)、式(17)和式(18)以及模糊数学中的多元扩张原理[13]可得河流平均流速的隶属函数为

(19)

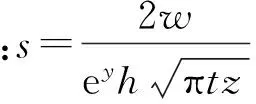
3 实例验证

实例数据来自文献[9]，表1为测定的原始数据及所需数据的计算结果，其中(Xi,Yi)是由测量值换算成的模糊线性回归模型中的自变量和因变量。在某河一侧的一点连续排放浓度c0=600mg/L，流量为q0=0.4m3/s的污水，而且已知污染物即示踪剂不可降解，时刻t=1 200s，该河的水深h=4m，河宽为50m。现以纵向距离x=1 200m为定值、沿河流横向不同距离处采取水样，即取y值不同的样本，测定污染物浓度值，根据试验数据应用模糊线性回归模型计算河流的平均流速v和横向扩散系数DT。此算例为一数字算例，其真值DT=0.01m2/s，v=1.0m/s。

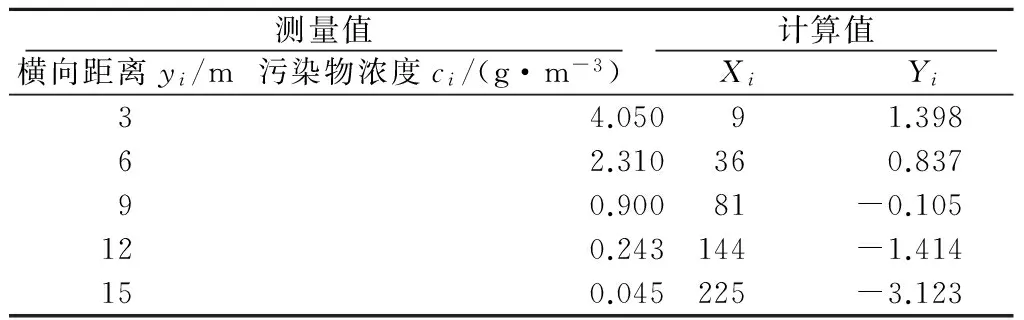
表1 观测原始数据及所需数据的计算结果Table 1 The original measured data and the calculated results

将表1中的数据(Xi,Yi)代入公式(14)，取置信水平λ=0.6，用Matlab编程计算正态模糊回归系数的参数如表2所示。

表2 模糊线性回归系数的参数Table 2 Parameters of the fuzzy linear regression coefficients

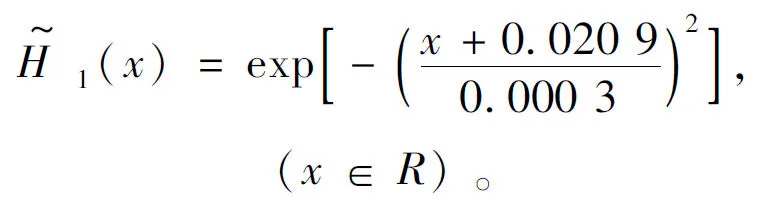
(20)

(21)

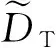
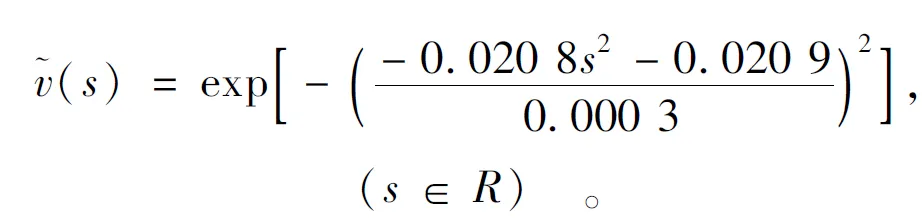
(22)

表3 不同置信水平下的河流参数取值区间Table 3 Ranges of river parameters in the presence of different confidence levels

4 结 语

在野外进行河流系统的示踪试验时，因河流系统自身的不确定性以及各种外界不确定因素的影响，将导致所测得的数据具有一定的模糊性。为此，建立模糊线性回归模型来确定河流的横向扩散系数和平均流速。应用所建模型可确定各正态模糊回归系数，并可通过各回归系数与参数间的关系确立各参数的隶属函数，进而确定在不同截集λ下参数的取值范围。通过实际算例验证，本方法估算的参数值与真值非常接近，证明本算法是可靠、合理的。并且与其他算法相比，本算法的参数选取更具有灵活性。采用模糊线性回归模型确定河流横向扩散系数和平均流速的取值均是区间，此方法可根据不同试验数据存在的误差大小和不确定因素的影响程度，选取恰当的置信水平，可得到不同要求下的河流水质参数的可能取值范围。

[1] 薛禹群.地下水动力学[M].北京:地质出版社,1997:171-178. (XUE Yu-qun. Dynamics of Groundwater Theory[M]. Beijing: Geological Press,1997:171-178.(in Chinese))

[2] 余常昭. 环境流体力学导论[M]. 北京:清华大学出版社，1992:180-181. (YU Chang-zhao. Introduction of Environmental Fluid Dynamics[M]. Beijing: Tsinghua University Press,1992:180-181. (in Chinese))

[3] 赵文谦.环境水力学[M].成都:四川科技大学出版社,1986:73-76. (ZHAO Wen-qian. Environmental Hydraulics[M]. Chengdu: Sichuan University of Science and Technology Press, 1986: 73-76. (in Chinese))

[4] 郭建青.示踪试验确定河流纵向弥散系数的直线图解法[J].环境科学, 1990,11(2):24-27. (GUO Jian-qing. Tracer Tests to Determine the Longitudinal Diffusion Coefficient of River Through Linear Graphic Method[J]. Chinese Journal of Environmental Science, 1990,11(2): 24-27. (in Chinese))

[5] 郭建青,王洪胜,李云峰.确定河流离散系数的相关系数极值法[J].水科学进展,2000,11(4):387-391.(GUO Jian-qing, WANG Hong-sheng, LI Yun-feng. Extreme Method to Determine the Correlation Coefficients of Dispersion Parameter of River[J]. Advances in Water Science, 2000,11(4):387-391.(in Chinese))

[6] 马洪波,崔柏林,常文娟.改进的BP网络模型在确定河流纵向离散系数中的应用[J].水电能源科学,2010,28(9):19-21. (MA Hong-bo, CUI Bo-lin, CHANG Wun-juan. Application of Improved BP Network Model to Determination of River Longitudinal Dispersion Coefficient[J]. Water Resources and Power, 2010, 28(9): 19-21. (in Chinese))

[7] 郭建青,李 彦,王洪胜,等.粒子群优化算法在确定河流水质参数中的应用[J].水利水电科技进展,2007,27(6):1-5. (GUO Jian-qing, LI Yan, WANG Hong-sheng,etal. Application of Particle Swarm Optimization Algorithms to Determination of Water Quality Parameters of River Streams[J]. Advances in Science and Technology of Water Resources, 2007,27(6):1-5. (in Chinese))

[8] 郭建青,李 彦,王洪胜,等.分析二维河流水质参数试验数据的相关系数极值法[J].水力发电学报,2010,29(4):102-106. (GUO Jian-qing, LI Yan, WANG Hong-sheng，etal. Correlation Coefficient Method to Analyse Two-dimensional Extreme Test Data of River Water Quality Parameters[J]. Journal of Hydroelectric Engineering, 2010,29(4):102-106.( in Chinese))

[9] 郭建青,张 勇.确定河流横向扩散系数的直线图解法[J].水利学报, 1997,(1):62-66. (GUO Jian-qing, ZHANG Yong. Linear Graphic Method to Determine Transverse Diffusion Coefficient of River[J]. Journal of Hydraulic Engineering, 1997,(1):62-66. (in Chinese))[10]MATHON B R, OZBEK M M, PINDER G F. Transmissivity and Storage Coefficient Estimation by Coupling the Cooper-Jacob Method and Modified Fuzzy Last-quares Regression[J]. Journal of Hydrology, 2008,353(3/4): 267-274.

[11]金士博，杨汝均. 水环境数学模型[M]. 北京:中国建筑工业出版社，1987. (JIN Shi-bo, YANG Ru-jun. Mathematical Model of Water Environment[M]. Beijing: China Architecture & Building Press,1987. (in Chinese))

[12]景英川.模糊线性回归模型中的拟合度问题[J].山西师范大学学报:自然科学版,2002,16(3):10-14. (JING Ying-chuan. Imitation Degree Problem in Fuzzy Linear Regression Model[J]. Journal of Shanxi Normal University: Natural Science Edition, 2002,16(3):10-14. (in Chinese))

[13]杨纶标,高英仪.模糊数学原理及应用[M].广州:华南理工大学出版社,2001: 171-174. (YANG Lun-biao, GAO Ying-yi. Principles and Applications of Fuzzy Mathematics[M]. Guangzhou: South China University of Technology Press, 2001: 171-174. (in Chinese))

(编辑：陈绍选)

Determining the Transversal Diffusion Coefficient of River ThroughNormal Fuzzy Linear Regression

ZHANG Zhuan1, CHANG An-ding2, WANG Yuan-ying2, WANG Xiao-chen2

(1.Shaanxi Institute of International Trade and Commerce, Xianyang 712046, China;2.School of Science, Chang’an University 710064, China)

To explore the method of calculating river’s diffusion coefficient in the presence of pollution, a normal fuzzy linear regression model was built, and through the membership function of fuzzy set, the ranges of water quality parameters (transversal diffusion coefficient and average flow velocity) in the presence of different confidence levels were calculated. The model was built based on linear graphic method, and the tracer test data of water mass was analysed based on fuzzy numbers. The water quality parameters calculated by this model were very close to the real values, which accounts for the feasibility and rationality of this model. It could also reflect the uncertainty of river system and the effects of other uncertainties in practice.

fuzzy linear regression; normal fuzzy number; membership function; transversal diffusion coefficient; average flow velocity

2014-02-26；

2014-03-03

中央高校基本科研业务费专项资金资助项目(310829130225)

张 转(1988-),女,陕西咸阳人,硕士研究生,主要从事最优化理论与方法研究，(电话)15202974335 (电子信箱)zhangzhuan10@163.com。

常安定(1964-),男,陕西大荔人,教授,硕士生导师,主要从事水文地质的数学方法研究，(电话)13389213296(电子信箱)chdanding@126.com。

10.3969/j.issn.1001-5485.2015.08.004

P641.8

A

1001-5485(2015)08-0022-04

2015,32(08):22-25,39