三种抛物线形渠道共轭水深的显式计算公式
代述兵,刘韩生,杨吉健
(西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100)
三种抛物线形渠道共轭水深的显式计算公式
代述兵,刘韩生,杨吉健
(西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100)
为了得到半立方、平方、立方抛物线形渠道共轭水深的显式计算公式,对这3种抛物线形渠道的水跃方程进行恒等变形,利用临界水深介于跃前水深和跃后水深之间的性质,得到了无量纲跃前水深x和无量纲跃后水深y之间的关系式,进一步分别得到其迭代公式。在工程常用范围内,利用excel拟合得到其迭代初值,提出了一套抛物线类渠道共轭水深的显式计算公式。最后,实例及误差分析表明:半立方、平方、立方抛物线形断面无量纲跃前水深x、无量纲跃后水深y最大相对误差分别为0.25%,-0.23%;0.17%,-0.29%;0.31%,0.39%。公式物理概念清晰,计算简捷,精度高,适用范围广。
半立方抛物线形断面;平方抛物线形断面;立方抛物线形断面;共轭水深;显式计算公式
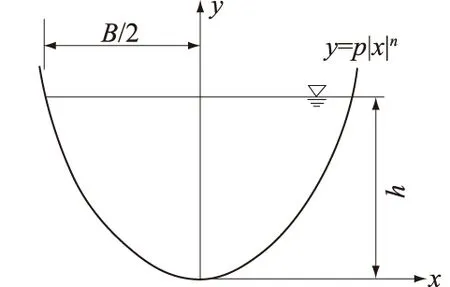
图1 抛物线类渠道断面Fig.1 Section of parabola- shaped channel
1 研究背景
抛物线形渠道的几何形状最接近天然河道,水流条件好,输砂率高,且具有耐冲刷、耐冻胀破坏、边坡稳定性较好的结构特点。近年来,抛物线形断面渠道在西部寒旱区灌溉排水工程、引水工程及城市供水工程中得到推广应用。共轭水深是水力学中一个重要参数,共轭水深传统的计算方法有试算法、图表法和计算机编程方法,但这些方法不便于工程实际应用。
目前对于梯形、城门洞形、马蹄形、圆形等断面共轭水深的计算已经取得了一些实用成果[1-5],对半立方、平方、立方抛物线形断面的正常水深、收缩水深、共轭水深等计算成果也取得一定进展,如:文献[6-8]对半立方、平方抛物线形断面正常水深进行了研究;文献[9]给出了半立方抛物线形断面收缩水深的计算方法;文献[10-12]对平方、立方抛物线形收缩水深进行了研究;文献[13-14]对平方、立方抛物线形渠道水力最优断面进行了深入研究;文献[15-16]给出了立方、半立方抛物线形渠道共轭水深的迭代计算,但迭代步骤繁琐;文献[17]给出了抛物线形断面共轭水深的计算公式,但精度偏低;文献[18]举例给出了MATLAB仿真平台求解平方抛物线形渠道共轭水深的计算机方法,但不便于工程应用。本文对半立方、平方、立方抛物线形渠道的水跃方程进行恒等变形,提出恰当的迭代格式,最终得到半立方、平方、立方抛物线形渠道共轭水深的显式计算公式。
2 共轭水深迭代公式的建立
抛物线类渠道断面见图1。
抛物线类断面方程为
y=p|x|n。
(1)
式中:p>0,n一般取1.5,2,3,即半立方、平方、立方抛物线形渠道。水深为h时,水面宽度为B。
棱柱体水平明渠水跃方程[19]为
(2)
式中:Q为流量(m3/s);g为重力加速度(m/s2);A1,A2分别为水跃前、跃后过水断面面积(m2);hc1,hc2分别为水跃前、跃后过水断面形心距水面的距离(m)。
半立方、平方、立方抛物线形渠道过水面积以及形心距水面距离如表1所示[15-18]。

表1 半立方、平方、立方抛物线形断面参数Table 1 Parameters of semi-cubic, square, and cubic parabola-shaped sections
注:h1,h2为跃前、跃后断面水深(m);p为形状参数;Q为流量(m3/s);g为重力加速度(m/s2)。
将半立方、平方、立方抛物线形渠道的跃前、跃后断面面积A1,A2以及跃前、跃后形心水深hc1,hc2代入式(2)分别得到其水跃方程为
(3)
利用临界水深hk介于跃前水深h1和跃后水深h2的性质,建立无量纲参数取值范围(0,1)的x,y,并化简得
(4)
将表1中半立方、平方、立方抛物线形断面临界水深hk代入式(4)中,并将得到的h1,h2分别代入式(3),得到水跃方程关于x,y的简化等式,即
(5)
引入量纲为一的共轭水深函数β,并令
(6)
已知跃后水深h2,那么由hk、式(4)、式(6)可求得y和β,则利用不动点迭代法可推得x的迭代公式。同理,已知跃前水深h1,则可推得y的迭代公式。半立方、平方、立方抛物线形渠道无量纲跃前、跃后水深x,y迭代公式并汇总如式(7)。
(7)
3 迭代公式收敛性的证明
根据迭代理论[7],方程x=φ(x)的一个根为N,则迭代公式xi+1φ(xi)收敛于N的条件为:在N的某一个领域|x-N|<δ内,迭代函数的一阶导数的绝对值小于某一个正数L,即|φ′(x)|≤L,且0 证明:由上述可知只需证明|φ′(x)|<1即可证明该迭代函数收敛。以半立方抛物线无量纲跃前水深迭代公式x=[(8+5x13/3)β]3/5为例证明。 φ(x)=[(8+5x13/3)β]3/5,对其求导数: (8) 而由式(6)半立方抛物线水跃方程可得 (9) 将式(9)代入式(8)得 (10) 由于跃前水深肯定比临界水深小,因而x<1,实际上,工程中常用的范围为x∈[0.1,0.7],因而φ′(x)<0.305 696<1,因此迭代公式x=[(8+5x13/3)β]3/5收敛。同理其余5个迭代公式收敛。 迭代计算收敛快慢主要取决于2个因素:迭代公式格式和迭代初值的选取是否恰当。只有在恰当的迭代公式与合适的迭代初值配合使用才能达到收敛快、精度高的目的。一般希望迭代初值尽可能接近真实值,迭代能用更少的步骤得到真实值,但经作者验证并非总是如此。迭代初值的函数形式也很重要,幂函数和线性函数比较,线性函数在没有幂函数精度高的情况下,线性函数在迭代过程中反而能更快逼近真值,更快收敛得到精度更高的结果,当然也得考虑公式的简捷程度,太复杂的迭代初值,也许精度很高但仍然暂不予考虑。 为了选取得到x,y的较优迭代初值,用excel得到了关于x,β和y,β的散点图,添加趋势线得到了x,β和y,β的直线关系,拟合相关系数达到0.99以上,此即为迭代初值。 半立方、平方、立方抛物线形断面的迭代初值分别为 (11) 迭代计算都很繁琐,迭代初值选取不恰当或迭代公式选取不合理,迭代几次甚至上十次均不能得到满意结果,本文仅需一次迭代就可得到精度较高的结果,将式(11)中半立方、平方、立方抛物线形断面迭代初值代入式(7)中相应的迭代公式,可得到精度较高的直接计算公式,即 (12) 半立方抛物线形断面无量纲跃前水深x最大相对误差为0.25%,无量纲跃后水深最大相对误差为-0.23%;平方抛物线形断面无量纲跃前水深x最大相对误差为0.17%,无量纲跃后水深最大相对误差为-0.29%;立方抛物线形断面无量纲跃前水深x最大相对误差为0.31%,无量纲跃后水深最大相对误差为0.39%,如图2。 图2 断面无量纲参数x,y相对误差分布Fig.2 Relative error distribution of dimensionless parameters x and y of the parabola-shaped sections 某半立方抛物线形渠道,方程为y=0.2|x|1.5,渠道流量Q=10 m3/s,渠道某处发生水跃,跃前水深h1=0.33 m,求跃后水深?若其他参数p,Q,h1均不变,只改变方程次数,平方抛物线、立方抛物线分别跃后水深为多少? 解: (1) 半立方抛物线: y=[5+8(7.43β+0.275)13/3]3/8β3/8=0.404 0。 (2) 平方抛物线: y=[0.6+(0.924β+0.25)4]2/5β2/5=0.391 8。 (3) 立方抛物线: y=[8+14(13.783β+0.192)11/3]3/7β3/7=0.379 6。 本文将半立方、平方、立方抛物线形渠道水跃方程通过无量纲跃前水深x和无量纲跃后水深y进行简化,给出了求解其跃前水深和跃后水深的迭代公式,并从理论上证明了迭代公式在工程常用范围内x∈[0.1,0.7]的收敛性,用直线方程拟合得到了迭代初值,提出了一套具有较高精度的共轭水深直接计算公式。通过实例计算和误差分析可知: (1) 建立的直接计算公式具有较高精度,半立方、平方、立方抛物线形断面无量纲跃前水深x和无量纲跃后水深y最大相对误差分别为0.25%,-0.23%;0.17%,-0.29%;0.31%,0.39%。 (2) 文中提出的计算式物理概念明确,适用范围广,通用性强,避免了在共轭水深计算中不能直接求解,需采用试算法、图表法等间接方法求解的繁琐和限制,为抛物线形渠道的设计、运行管理等提供参考。 [1] 刘计良,王正中,杨晓松,等.梯形渠道水跃共轭水深理论计算方法初探[J].水力发电学报, 2010,29(5):216-219. (LIUJi-liang,WANGZheng-zhong,YANGXiao-song, et al.PreliminaryStudyontheTheoreticalMethodforCalculatingConjugateDepthofTrapezoidalChannel[J].JournalofHydroelectricEngineering, 2010, 29 (5): 216-219. (inChinese)) [2] 马吉明,谢省宗,梁元博.城门洞形及马蹄形输入隧洞内的水跃[J].水利学报,2000, (7): 20-24. (MAJi-ming,XIESheng-zong,LIANGYuan-bo.HydraulicJumpsinRectangularConduitwithCircularUpperWallandHorseshoeTunnel[J].ShuiliXuebao, 2000, (7): 20-24. (inChinese)) [3] 冯家涛.梯形渠道水跃共轭水深直接计算公式[J].力学与实践,1998,20(5):50-51. (FENGJia-tao.ADirectCalculationFormulaforConjugateWaterDepthofWaterJumpinaTrapezoidChannel[J].MechanicsinEngineering, 1998,20(5): 50-51. (inChinese)) [4] 李 蕊,王正中,张宽地,等.梯形明渠共轭水深计算方法[J].长江科学院院报,2012,29(11): 33-36. (LIRui,WANGZheng-zhong,ZHANGKuan-di, et al.CalculationMethodforConjugateWaterDepthinOpenTrapezoidalChannel[J].JournalofYangtzeRiverScientificResearchInstitute, 2012, 29(11): 33-36. (inChinese)) [5] 郭振家,刘伟哲,马 玉,等.圆形断面水跃共轭水深的迭代计算方法[J].吉林水利,2013, (1): 7-9. (GUOZhen-jia,LIUWei-zhe,MAYu, et al.IterativeMethodofConjugateDepthforChannelswithCross-section[J].JilinWaterResources, 2013, (1): 7-9. (inChinese)) [6] 张新燕,吕宏兴.抛物线形断面渠道正常水深的显示计算[J].农业工程学报,2012,28(21):121-125. (ZHANGXin-yan,LVHong-xing.ExplicitSolutionforNormalDepthinParabolic-shapeChannel[J].TransactionsoftheCSAE, 2012, 28(21): 121-125. (inChinese)) [7] 赵延风,王正中,方 兴,等.半立方抛物线形渠道正常水深算法[J].排灌机械工程学报,2011,29(3):242-245. (ZHAOYan-feng,WANGZheng-zhong,FANGXing, et al.CalculationMethodforNormalDepthofSemi-cubicParabolicChannels[J].JournalofDrainageandIrrigationMachineryEngineering, 2011, 29(3): 242-245. (inChinese)) [8] 藤 凯.半立方抛物线形渠道正常水深的近似计算公式[J].长江科学院院报,2012,29(12):30-33. (TENGKai.TheApproximateFormulaforNormalWaterDepthofSemi-cubicParabolicChannels[J].JournalofYangtzeRiverScientificResearchInstitute, 2012, 29(12): 30-33. (inChinese)) [9] 文 辉,李风玲.立方抛物线断面渠道收缩水深的直接计算方法[J].人民长江,2009,40(13):38-59. (WENHui,LIFeng-ling.TheDirectCalculationMethodofContractionDepthfortheCubicParabolic-shapedChannel[J].YangtzeRiver, 2009, 40(13): 38-59. (inChinese)) [10]文 辉,李风玲.抛物线形断面渠道收缩水深的解析解[J].长江科学院院报,2009,26(9):32-34. (WENHui,LIFeng-ling.AnalyticalSolutionofWaterDepthinParabolic-ShapedChannelwithContractedSection[J].JournalofYangtzeRiverScientificResearchInstitute, 2009, 26(9): 32-34. (inChinese)) [11]赵延风,宋松柏,孟秦倩.抛物线形断面渠道收缩水深的直接计算方法[J].水利水电技术,2008,39(3):36-41. (ZHAOYan-feng,SONGSong-bai,MENGQin-qian.ADirectCalculationMethodforWaterDepthinParabolic-shapedChannelwithContractedSection[J].WaterResourcesandHydropowerEngineering, 2008, 39(3): 36-41. (inChinese)) [12]冷畅俭,王正中.三次抛物线形渠道断面收缩水深的计算公式[J].长江科学院院报,2011,28(4):29-35. (LENGChang-jian,WANGZheng-zhong.FormulaforCalculatingContractedWaterDepthofChannelwithCubicParabolaCrossSection[J].JournalofYangtzeRiverScientificResearchInstitute, 2011, 28(4): 29-35. (inChinese)) [13]张志昌,刘亚菲,刘松舰.抛物线形渠道水力最优断面的计算[J].西安理工大学学报,2002,18(3):235-237. (ZHANGZhi-chang,LIUYa-fei,LIUSong-jian.TheCalculationofOptimalHydraulicCrossSectioninParabola-ShapeCanal[J].JournalofXi’anUniversityofTechnology,2002,18(3): 235-237. (inChinese)) [14]魏文礼,杨国丽.立方抛物线形渠道水力最优断面的计算[J].武汉大学学报(工学版),2006,39(3):49-51. (WEIWen-li,YANGGuo-li.CalculationofOptimalHydraulicCross-sectionforCubicParabola-shapeChannel[J].EngineeringJournalofWuhanUniversity, 2006,39(3):49-51. (inChinese)) [15]马子普,张根广,赵春龙,等.立方抛物线形渠道水跃共轭水深的迭代算法[J].人民长江,2013,44(1):90-92. (MAZi-pu,ZHANGGen-guang,ZHAOChun-long, et al.TheIterativeFormulaoftheCubicParabolic-shapedChannel’sConjugateDepth[J].YangtzeRiver, 2013, 44(1): 90-92. (inChinese)) [16]马子普,张根广,冯 雪,等.半立方抛物线形明渠共轭水深的迭代算法[J].西北农林科技大学学报(自然科学版),2012,40(11):211-215. (MAZi-pu,ZHANGGen-guang,FENGXue, et al.IterativeAlgorithmofConjugateDepthforSemi-cubicParabolicOpenChannels[J].JournalofNorthwestA&FUniversity(NaturalScienceEdition), 2012, 40(11): 211-215. (inChinese)) [17]冷畅俭,王 弈,王正中.抛物线形断面渠道共轭水深的直接计算公式[J].排灌机械工程学报,2013,31(2):132-136,141. (LENGChang-jian,WANGYi,WANGZheng-zhong.ExplicitCalculationEquationsforConjugateDepthsofChannelsinParabolic-shapedCross-section[J].JournalofDrainageandIrrigationMachineryEngineering, 2013, 31(2): 132-136, 141. (inChinese)) [18]汪 清,曹 青,马子普.二次抛物线形渠道临界水深与共轭水深简化算法[J].水电能源学,2012,30(6):111-113. (WANGQing,CAOQing,MAZi-pu.SimplifiedCalculationMethodofCriticalDepthandConjugateDepthforSecond-degreeParabolicChannels[J].WaterResourcesandPower, 2012, 30(6): 111-113. (inChinese)) [19]吕宏兴,裴国霞,杨玲霞.水力学[M].北京:中国农业出版社,2002. (LVHong-xing,PEIGuo-xia,YANGLing-xia.Hydraulics[M].Beijing:ChinaAgriculturalPress, 2002. (inChinese)) [20]李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2008. (LIQing-yang,WANGNeng-chao,YIDa-yi.NumericalAnalysis[M].Beijing:TsinghuaUniversityPress, 2008. (inChinese)) [21]郑阿奇,曹 弋.MATLAB实用教程[M].北京:电子工业出版社,2007. (ZHENGA-qi,CAOYi.PracticalTutorialofMATLAB[M].Beijing:PublishingHouseofElectronicsIndustry, 2007. (inChinese)) (编辑:刘运飞) ExplicitCalculationFormulaofConjugateDepthforThreeKindsofParabola-shapedChannels DAI Shu-bing, LIU Han-sheng,YANG Ji-jian (College of Water Resources and Architectural Engineering,Northwest A & F University, Yangling 712100, China) In order to get the explicit calculation formula of conjugate depth for semi-cubic, square, and cubic parabolic-shaped channels, the jump equations of the three parabola-shaped channels were transformed identically and the relationships between the dimensionless water depthxbefore jump and the dimensionless water depthyafter jump were obtained according to the property that the critical depth was between the pre-jump depth and the post-jump depth. Their iterative formulas were further obtained respectively. Hence, a set of explicit calculation formulas of conjugate depth for semi-cubic, square, and cubic parabolic-shaped channels were obtained by fitting the iterative initial value through excel in common engineering scope. Finally, example and error analysis shows that the absolute value of maximum relative error of dimensionless water depthxbefore jump was 0.25%, 0.17%, and 0.31% respectively for the semi-cubic, square, and cubic parabolic-shaped channel, and that of dimensionless water depthyafter jump was respectively -0.23%, -0.29%, and 0.39%. The formulas were convenient and highly accurate with clear physical meaning and wide application scope. semi-cubic parabola-shaped channel; square parabola-shaped channel; cubic parabola-shaped channel; conjugate depth; explicit calculation formula 2014-02-26; 2014-03-17 代述兵(1990-),男,四川安岳人,硕士研究生,主要从事水工建筑物与高速水流方面的研究,(电话)15109217838(电子信箱)daishubing1990@163.com。 刘韩生(1962-),男,陕西韩城人,教授,博士,主要从事水工建筑物与高速水流方面的研究,(电话)13319231569(电子信箱)hanshengliu@126.com。 10.3969/j.issn.1001-5485.2015.08.009 TV131.4 A 1001-5485(2015)08-0051-06 2015,32(08):51-564 迭代初值的选取及共轭水深计算公式
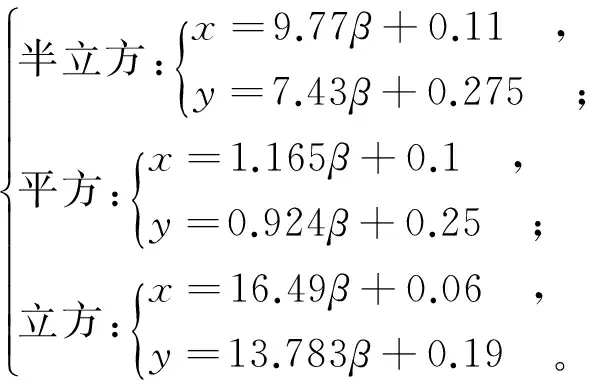
5 直接计算公式的误差分析
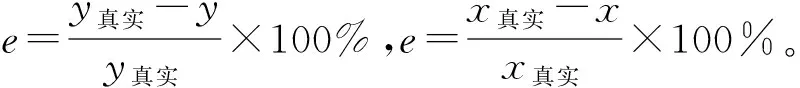

6 算 例
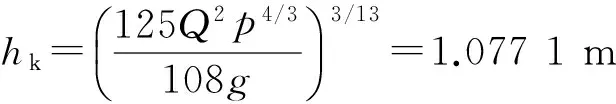
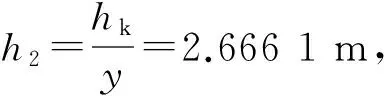
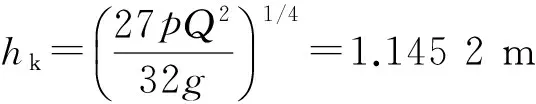
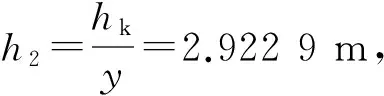
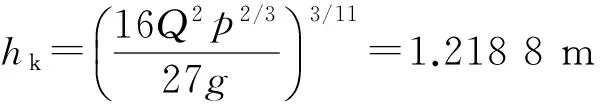
7 结 论

