一类绝对值函数的性质及应用
☉山东省临清市实验高中 姚继新
一类绝对值函数的性质及应用
☉山东省临清市实验高中 姚继新
近几年,考查绝对值函数f(x)=|mx-a|±|nx-b|(m>0,n>0,a≠b)的图像与性质的试题越来越多,而该类函数又恰恰是学生感觉非常疑惑的地方,因此,笔者做一整理,以飨读者.
为方便起见,我们约定:
(1)f(x)=|x-a|+|x-b|为f(x)=|mx-a|+|nx-b|(m>0,n>0,a≠b)的标准型,f(x)=|x-a|-|x-b|为f(x)=|mx-a|-|nx-b|(m>0,n>0,a≠b)的标准型;
(2)使|x-a|=0的x的值为|x-a|的零点;
(3)以下均有m>0,n>0,a≠b.
一、对函数f(x)=|mx-a|+|nx-b|(a≠b)的研究
1.若m=n=1,则f(x)=|x-a|+|x-b|,为f(x)=|mx-a|+|nxb|的标准型.
①由绝对值的几何意义知:标准型函数f(x)的几何意义为数轴上的点x到a、b的距离之和;
②当a≤x≤b(不妨设a<b)时,f(x)取到最小值|b-a|;
③其图像为U形折线,如图1.
(2)若m=n≠1,则f(x)=|mx-a|+|nx-b|=进而转化为标准型.
(3)若m≠n.

图1

图2

图3

图4
二、对函数f(x)=|mx-a|-|nx-b|(a≠b)的研究
类比对函数f(x)=|mx-a|+|nx-b|(a≠b)的研究,可得以下结论:
(1)若m=n=1,则f(x)=|x-a|-|x-b|,为f(x)=|mx-a|-|nx-b|的标准型.
①由绝对值的几何意义知:标准型函数f(x)的几何意义为数轴上的点x到点a的距离减去点x到点b的距离;
②当a≤x≤b(不妨设a<b)时,f(x)取到最大值|b-a|;③其图像为Z形折线,如图5,)为其对称中心.

图5
(2)若m=n≠1,则f(x)=|mx-a|-|nx-b|=|m|·),进而转化为标准型.
(3)若m≠n.

图6
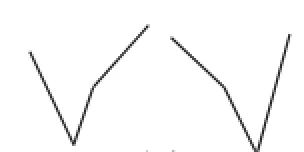
图7
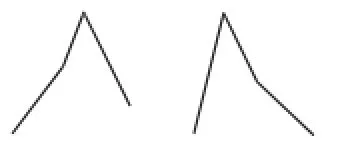
图8
(i)若m>n,则其图像如图7所示;
(ii)若m<n,则其图像如图8所示.
事实上,当m、n不满足m>0、n>0的条件时,也可先转化为m>0、n>0的形式,进而求解.
例1 (2013年高考山东理14)在区间[-3,3]上随机取一个数x, 使得|x+1|-|x-2|≥1成立的概率是__________.
分析:利用f(x)=|x+1|-|x-2|的几何意义,知当1≤x≤ 3时满足不等式,故由几何概型知答案为
例2 设函数f(x)=|x+3|-|x-a|(a≠-3)的图像关于点(1,0)中心对称,则a的值是_________.
分析:f(x)=|x-a|-|x-b(|a≠b)的图像关于点)中心对称,故即a=5.
例3 设函数f(x)=|2x+1|+|ax|,若存在三个互不相等的实数x1、x2、x3,使得f(x1)=f(x2)=f(x3),则实数a=______.
分析:由题意知f(x)的图像必是U形图像,故|a|=2,即a=±2.
例4 已知函数f(x)=|x-1|+|x-2|.
(1)画出函数f(x)的图像;
(2)若不等式|a+b|+|a-b|≥|a|·f(x)(a≠0,a、b∈R)恒成立,求实数x的取值范围.
分析:(1)略.
(2)由|a+b|+|a-b|≥|a|·f(x),知f(x)恒成立.

