拓展“活”教材 演绎“好”数学——以“赵爽弦图中的不等式性质再探究”为例

☉福建省福州第三中学 林珍芳

拓展“活”教材 演绎“好”数学
——以“赵爽弦图中的不等式性质再探究”为例

☉福建省福州第三中学 林珍芳

2014年12月，笔者有幸参加了中国教育学会中学数学教学专业委员会组织的全国高中青年数学教师优秀课展示和培训活动，进行了课题为“赵爽弦图中的不等式性质的再探究”的教学展示.赛后，笔者对这节课进行了回顾与反思.

教材是连接课程方案与教学实践的枢纽，是教学的载体.新课程倡导教师“用教材”而不是简单的“教教材”，古人云“书不尽言，言不尽意”，所以教师需要通过对教材“再加工”，将简单、静态、固化的教材内容，设计为丰富、生动、开放的“课本剧”，促进学生内化知识、主动探究，领悟数学本质.基于此，笔者设计了高三复习探究课“赵爽弦图中的不等式性质的再探究”.本探究课是以赵爽弦图为载体，以问题为线索，以TI-NspireCX-C CAS（图形计算器）为手段，搭建探究平台，引导学生学会发现、学会探究、学会学习，真正活化教材，传递数学教学的正能量.

一、再现“弦图”，唤醒知识

建构主义教学理论认为每一个知识都不是凭空生成的，必须有一定的经验基础.“温故知新”是教学永恒的规律.学生在初中时通过赵爽弦图认识了勾股定理，赵爽弦图结构精妙，内涵丰富，是数与形完美统一的典范.在推导基本不等式时学生再次研究赵爽弦图，一样的图形背景，不同的问题指向，从等量关系（勾股定理）到不等关系（基本不等式），从平面几何到不等式的研究，是知识和思维的延续、拓展.

师：2002年8月国际数学家大会在北京召开，这个大会颁发的菲尔茨奖相当于数学界的诺贝尔奖.大会的会标是根据中国古代的数学家赵爽的弦图设计的，颜色的明暗使它看上去像一个风车，代表中国人民的热情好客.

师：（如图1、2）请同学们回忆一下以前借助赵爽弦图主要研究了什么？

图1

图2

生1：赵爽弦图是由两个正方形和四个全等的直角三角形构成的.如果设大正方形边长为c，直角三角形的两条直角边分别是a，b（a＞b），利用S大正=4S直角+S小正，得到c2=a2+b2，这就是勾股定理.

生2：除了等量关系，我们还利用了S大正≥4S直角，得到a2+b2≥2ab，经过换元得到这就是基本不等式.

师：很好，同学们不仅记住了基本不等式的结论，而且对它的推导过程和转化方法熟稔于心，为我们进一步的研究奠定了扎实的基础.其实，赵爽弦图的内涵远不止这些，今天，我们一起来深入探究弦图中蕴含的其他有趣的不等关系.

教学断想：美国教育家加涅认为：教新知识之前，必须先激活学生长时间记忆中相关的原有知识.公式本身就是一个经典的数学问题，它的生成、发展过程蕴含着经典的数学思想和方法.赵爽弦图的直观再现，基本不等式的重新回顾，唤醒了学生对变与不变的关系、整体与局部的关系、等与不等的关系、一般与特殊的关系的感受，促使学生在直观丰富的情境下感知公式的基本特征和形式，有效强化“抽象知识”和“几何原型”之间的本质联系.

二、追问“弦图”，体验发现

“问起于疑，疑源于思”.问题是引发学生思维和探索活动的向导.创设适度并有一定力度的问题是探索的前提，是驱动数学学习的原动力.新课程理念提倡将学习内容以一个或多个具有较高思维价值的开放性问题呈现，教师要善于在学生理解知识的困惑处、思维的突破点设计有趣、有效的问题串，由浅入深、层层递进，充分揭示问题、知识、思想的内在联系与数学本质，让学生在了解知识来龙去脉的同时，积极思考，勇于质疑，不断追问.

师：在赵爽弦图中，四个小的直角三角形是重要的图形元素，如果将四个小直角三角形各边中点连接构成一个正方形MNOH，那么此时正方形MNOH的面积是否与四个直角三角形的面积和也存在恒成立的关系？（如图3）

图3

图4

生3：我用函数的方法研究这个问题，设正方形边长为a（a=10），直角三角形斜边上的高的垂足为T，AT=x，由于中点正方形MNOH的面积为50cm2，四个直角三角形面积对应的函数为在同一个直角坐标系中作出它们的函数图像（如图4），当0.7＜x＜9.8时，四个直角三角形面积和大于中点正方形MNOH的面积，当0＜x＜0.7或9.8＜x＜10时，大小关系则相反，当x=0.7或x=9.8时，它们面积相等，所以不存在恒成立的不等式.

生4：按照这个构造方式，过四个直角三角形的顶点引正方形ABCD各边的垂线，那么四个垂足也构成正方形MNOH，那么这样构成的正方形面积与四个直角三角形的面积的和大小关系又是如何？（如图5）

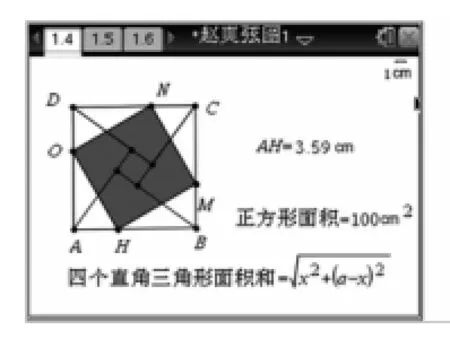
图5

图6

图7

生5：我通过图形计算器的作图功能和zeros命令（解方程），发现当0.022625＜x＜9.97738时，四个直角三角形面积的和大于垂足正方形MNOH的面积，否则相反，所以它们不存在恒成立的不等关系.（如图6，图7）

师：很好！大家借助图形计算器的模拟仿真功能作出函数的图像，进而探究问题.这是利用图形计算器研究数学的优势和特点.

赵爽弦图蕴含着勾股定理和基本不等式内容体现了直角三角形直角边a、b（a＞b）和斜边c的关系.作为直角三角形的重要元素——斜边上的中线和斜边上的高线，能否探究出其中蕴含着哪些不等关系？

生6：根据直角三角形中斜边大于直角边的性质，在Rt△ABE中，过点E作EH⊥AB于点H，取AB中点M，连接ME，我发现EH≤ME，即h（如图8）

生7：由直角三角形斜边上的高的问题容易联想到直角三角形的面积，即，则因为所以两边平方得左边分子分母同除以a2b2，得到

（其他学生啧啧称奇）

（课堂上洋溢着阵阵赞许声）

图8

师：如果我们把生7、生8的结论稍作整理，就会得到美妙的不等关系，由可以写成生8得到≤ab，由于a2+b2≥2ab，所以得到重要的不等式关系若把a2、b2看成两个正数，就得到均值不等式链

上述的发现正是基于直角三角形中斜边上的中线、斜边上的高之间内在的几何不等关系，探究得到了赵爽弦图中蕴含的重要的不等关系——均值不等式链，看似平常却奇绝，形数相映出新意.

教学断想：在公式教学中不少教师只是满足于将教材的结论和证明“依样画葫芦”，浅尝辄止，使得公式教学只是蜻蜓点水、盲目模仿、题海战术，片面强调套用公式的技巧，热衷于进行解题训练，忽视公式的来源及其蕴含的丰富的思想方法.教师通过对赵爽弦图中几何性质的追问，引导学生对本质问题深刻挖掘，领悟几何与代数之间的内在联系.从赵爽弦图中直角三角形的直角边、斜边、斜边上的中线、斜边上的高的几何关系中引申出基本不等式及其衍生结论，让学生自由自在、灵活地思考，促进学生在原有知识和经验基础上的主动建构，实现了知识的自然过渡和传承间的“春风化雨，润物无声.”

三、深探“弦图”，跨界交汇

探究性学习的特征之一是教学过程的探索化.著名教育家乔治·波得亚曾说：“最好的数学学习方法是通过自己的发现获得知识，而发现的过程即是探索的过程.”所以探究性教学的焦点应放在知识的探索过程和获得知识的方法上.课堂上师生借助TI-NspireCX-CCAS（图形计算器）把静态的数学现象演绎成动态的探究过程，让学生用眼观察，动手实验，用脑思考，用心探索，就像一个小数学家一样提出问题、分析问题、解决问题，在渐行渐远中体会数学多元关联、动态演变、数形相关、辩证转化的特点.

师：上述过程中，我们着重从平面几何中线段的关系去挖掘和思考a、b的不等关系.如果我们用动态的观点研究，那么能否有新的视角和新的手段来探究其中的不等关系呢？现在我们利用图形计算器的动画功能，让赵爽弦图动起来，通过观察看到a、b在变化，c不变，那么a+ b的变化是否有什么规律？

生9：我发现，在变化过程中，a+b似乎有上界.

生10：用TI-NspireCX-CCAS（图形计算器）模拟发现，点E的轨迹是圆的四分之一.（如图9）

师：生11看到了变化的“弦图”中点E的运动与∠EAB的变化相关.所以引入角作变量，把a、b这两个变量通过消元转化为同一个角的问题，再利用三角函数求最值.这是一种用运动、转化的观点思考和解决问题，实现了利用三角函数来研究不等式的转化，超越了之前用平面几何来研究不等关系的想法.

图9

图10

生12：（如图10）从方程角度还可以看到a2+b2=c2是以原点为圆心，c为半径的圆，由于a≥0，b≥0，所以（a，b）是圆弧上的一个动点.通过整体换元令a+b=t，则b=-a+t，问题转化为直线与圆弧有交点.当直线与圆弧相切，易求得t=c或.则化简得（a+b）2≤ 2（a2+b2），即

师：生12的思路更灵活.他将勾股定理联想到圆的方程，实现了不等式和解析几何的跨界联手，展示了数形结合思想的巧妙转化.由开方得这也是一个著名的不等式，即为a、b的算术平均数和平方平均数之间的关系.

师：看来大家都是好眼力呀！静与动，方与圆，不等式与三角函数、解析几何在弦图中有机交融，演绎着数学的精彩.只要大家勤思考，勤动脑，就能发现许多隐藏在平凡图形中的数学奥秘.

教学断想：上述过程是通过搭建符合学生认知规律的脚手架，在学生亲手操作、亲历体验过程中，在运动和变化的过程中进行跨界联想，多元交汇，从三角函数、解析几何等角度观察、分析和解决问题，不断丰富知识探究过程的真切感和思考层次，使得学生对弦图的探究能够“横看成岭侧成峰，远近高低各不同”，从不同角度理解数学的本质.正如富兰克林说的那样：告诉我，我会忘记；教给我，我可能记住；让我参与，我才能学会.这种感悟是深刻的，永恒的.

四、重构“弦图”，彰显创意

数学学习过程是一个知识内化、思想熏陶、主动发现、主动发展的过程.“数学教学的核心是学生的‘再创造’，这种‘再创造’并非机械地重复历史中的‘原始创造’，而是根据自己的体验并用自己的思维方式重新去创造有关的数学知识”（数学教育家弗洛登塔尔语）.教学的意义在于学生探索的欲望、心智的觉醒、智慧的生长.叶澜教授曾经充满诗情画意地说过：“课堂应该是向未知方向挺进的旅程，随时都有可能发现意外的通道和美丽的风景，而不是一切都必须遵循固定线路而没有激情的行程.”教学中的预设与生成常常是相生相伴，教师应因势利导，善于倾听，捕捉智慧，敏锐把握不期而至的生成性教学资源，让从知识课堂走向智慧课堂，为学生智慧的生长而教学.

师：今天我们通过挖掘赵爽弦图中的几何性质，用不同方法得到基本不等式链体现了数形结合、转化与化归的思想，展现赵爽弦图的无限魅力.

（这时有学生举手，示意要发言）

生13：赵爽弦图是在正方形中构造直角三角形，我思考能否在正三角形中构造类似的“弦图”来推导基本不等式，但我只是猜想，还没想出证明的方法.

师：这个问题提的好，老师先前备课时还没有想过这个问题，大家不妨一起来试试看.

生14：我们可以把之前利用面积的整体与部分的不等关系类比到正三角形（如图11）.在正三角形中，S小三角形=

（独特的视角、新颖的创意不仅赢得了阵阵掌声，也掀起了更高的探究创造的高潮）

生15：我有新的想法.因为正方形是特殊的菱形，所以我把弦图的大正方形设计为边长夹角为α的菱形（如图12，图13），不知能否推导出基本不等式.

（顿时课堂上一片寂静）

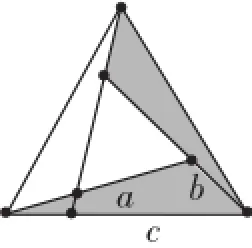
图11

图12

图13

师：大家的想法都非常有创意，都超乎了老师的预设.有道是“节外生枝处常有暗香来”，你们能抓住问题的本质，运用类比的方法设计“私人定制”的弦图可喜可贺，你们的猜想是否正确，有待课后继续研究.

教学断想：数学课堂常常因为动态生成而活跃，师生因为动态生成而成长，教学因为动态生成而充满生命的律动.学生能够运用类比的方法猜想并重构赵爽弦图，在“变”的现象中发现“不变”的本质，从“不变”的本质中探索“变”的规律，设计私人定制的“弦图”，探索推导基本不等式的新途径，是一种超越，是一种创意.虽然出乎意料之外，但又在情理之中，是难忘的一次不曾预约的精彩.

好的数学教学应当兼顾数学教育的知识取向与价值取向，将知识教学与价值观影响融为一体.赵爽弦图不仅具有丰富的数学内涵和人文价值，而且还具有深邃和广泛的教学作用和意义.教师只有充分挖掘并优化教材中的经典内容，这样才能唱响数学课堂“好声音”.

1.王跃辉，黄益全.高中数学人教课标版“基本不等式”教材研读［J］.中学数学教学参考（上），2013（1-2）.

2.王岳.高三复习课“三角函数的值域与最值”的教与思［J］.中学数学月刊，2012（11）.

3.偶伟国.MPCK视角：“以“基本不等式”为例［J］.中学数学教学参考（上），2013（10）.F

注：本文是福建省电化教育馆教育信息技术研究课题（闽电教馆kt412）《基于T3的数学教学转型与优化的研究》的成果.