两道测试题失分原因分析思考与启示

☉安徽省砀山中学 辛 民

两道测试题失分原因分析思考与启示

☉安徽省砀山中学 辛 民

一次高三数学质量测试中，有两道试题学生都可以通过读题、审题、分析、归纳、抽象、概括等活动，利用基本概念，构造自然、简洁的方法求解，然而，测试的结果出人意料，学生失分较多，这一现象引起了笔者的关注、思考、分析、探究、反思.现将其过程展示如下，与同行分享.

一、测试题及解答

例1 如图1.在△ABC中，AB=2，AC=1，∠BAC=120°，O为△ABC的外心.

（1）设A—→B=a，A—→C=b，OM⊥BC于点M，点P为直线OM上的任意一点，试判断A—→P·（a-b）是否为定值，并说明理由.

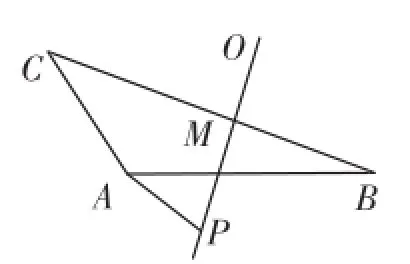
图1

（2）试用向量A—→B、A—→C表示A—→O.

分析：以三角形为载体，将三角形的外心与向量的数量积的运算、平面向量的基本定理等基础知识结合命题，考查平面向量的运算等知识，要求学生具有一定的利用数形结合、函数与方程思想方法分析、解决问题的能力，适合学生练习，巩固基础知识，提高能力，属于中等难度，不料测试的结果难度为0.27.仔细翻阅学生试卷，所教的班级解答较好的学生均采用参考答案给出的如下方法.

解：（1）如图2，以A为原点，AB所在的直线为x轴，建立直角坐标系，则A（0，0），的中垂线方程为x=1，AC的中垂线方程为），联立两中垂线方程，解得故

事实上，本题可利用向量的有关概念构造如下基本、简洁解法.

例2 如图3，已知直线4x-3y+3=0与单位圆交于A、 B两点，劣弧AB所对的圆心角为α，则tan）的值为（ ）.

图2

图3

分析：以学生熟悉的直线与单位圆的位置关系为依托命制试题，考查三角函数的定义、诱导公式、方程的解等基本知识，突出考查数形结合思想方法及分析问题、解决问题的能力，测试难度0.35.调查了解学生的解题方法，结果令人吃惊，学生都是利用点到直线的距离公式，以及的正弦、余弦、倍角与诱导公式求解.

事实上，利用三角函数的概念基本解法如下：

二、座谈交流

1.答题及试卷讲评回顾

学生普遍反应：对于例1，通过读题、审题、分析、抽象、概括等活动，回顾以前的解题经验及题型选用建立平面直角坐标系解决问题，运算量较大，无法得到正确的结果，对而不全.虽然题目条件有由向量的概念，但是通过读题、审题，没有形成向量意识，不能灵活、正确地将有关三角形的知识与向量的概念链接，如第（1）问由A—→P不能转化为M—→P-M—→A达到简化运算的目的，第（2）问由O为△ABC的外心不能形成向量A—→O在向量A—→B上的射影为1的概念，从而有效地建立等量关系式，达到迅速解题的目的.对于例2，读题后圆与直线相交图形在头脑中印象深刻，联想到半径、弦及圆心到弦的垂线构成直角三角形中含有角，因此利用解直角三角形求解，公式记忆不准确、运算错误导致结果不正确，会而不对，由于平时很少利用三角函数概念解题，虽然题目中的条件直线与单位圆相交于点A、B，没有在头脑中出现射线OA、OB，从而没有联想到三角函数的定义，构造方程组求解.

教师讲评试卷前调查：大部分学生对考试时解题方法进行修改订正得到了正确答案，认为学生已经解决了问题，没必要再进行仔细评讲，只需简单的点评强调一下运算、对对答案即可，教师没有真正坐在一起仔细分析学生失分的深层次的原因，失去了检测的意义.

2.原因分析

由座谈教师分析认为：解析几何引入坐标法使部分数学试题有了统一规范的解法，但是也给我们的教学带来一些负面的影响，教师和学生往往热衷于通过量的计算验证几何的一些性质，轻视概念教学、学习，不会或不愿由概念出发通过几何的特征思考问题、数量之间的关系，忽视作为几何图形所特有的属性要求，使得问题的解决流于表面，缺乏对问题的本质理解，长此以往，学生不能养成由基本概念出发思考、分析、解决问题的数学思维习惯，遇到问题只会机械地对题型、寻套路，这也是当前数学教学的一大弊端.

高中数学教师普遍对运算教学不重视，认为运算教学是次要的、枯燥的，也不需要动脑筋去思考，思维价值较低，不需要花功夫去应付，不少学生平时用计算器代替笔算、心算等.追求功利化教学效果，重视例题的选择讲解轻视配套练习的设计，重视题型归纳轻视条件与基本概念属性链接、解题方法的构建，重视解题技巧记忆轻视思想方法的概括；概念复习重复高一、二的故事，忽视对概念内涵、外延的挖掘、解读、理解；学生重视课堂听讲轻视课后反思归纳、练习实践，计算、思维能力提升无从谈起，运算能力的低下影响思维能力的提升，思维能力薄弱导致学生算理混乱、算法模糊，判断、选择能力低下，解题时对上题型、套路无法得到正确的结果，面对新的情境无法从多种表征中分析出本质属性，实现题设与概念对接，形成正确、有效的应用概念的解题方法.

试卷讲评教师没有真正理解学生解题因何而错、错误的地方、产生错误的原因是什么？不知道思想方法的缺失根本症结所在，产生缺失的原因是什么？不了解学生的想法、错误、纠结之处，仅仅注重结果的正确与否、问题是否解决？不能根据学生暴露的问题采取相应的教学策略，对症下药，促进学生对数学知识及思想方法理解的提升，培养学生良好的解题习惯，形成较为扎实的解题技能.

三、教学启示

1.提升自身素质领悟数学本质

数学概念作为反映现实世界的空间形式和数量关系的思维形式，是一类对象本质属性的反映，是数学知识的最基本内容、学科系统精髓和灵魂；是数学认知结构的重要组成部分，是构建数学理论的基石、导出数学定理、数学法则、解决问题的逻辑基础.解题过程即在基本概念理解的基础之上对问题的本质属性分析、概括、比较、联想、判断、推理、论证等的思维活动，自然、简洁的解题方法源于对问题本质深层次的理解与概括，由此可见，一个人数学能力的高低取决于对数学对象本质属性的理解掌握的深浅.从以上两题的答题及教学可以看出，教师自身要加强对数学对象本质属性的研究，站在数学整体高度上理解概念，领悟数学概念的形成过程、内涵与外延，以及数学对象本质的抽象与概括，挖掘基本概念蕴含的智力开发价值及数学思想方法的教育价值，养成“回归概念，从基本概念、基本原理出发，分析、思考问题本质属性，从概念的联系中寻找解决问题的思维方法”解题习惯.自觉地把研究概念、解读概念、应用概念根植于整个高中数学的教学、研究中去.

2.加强基础复习提高运算能力

运算技能是数学的基本能力，它是解题的基本功，也是学生发展思维能力、取得高分的根本保证，其重要性是不言而喻的，以上两题所考查的运算技能，主要包括方程、方程组求解，字母及无理数的运算等，从学生答题情况看却令人担忧，相当一部分学生运算能力不过关，如例1无理数的四则运算不准确，数量积、直线斜率计算出错，方程组不能正确求解等，例2点到直线的距离、半角、和角公式不能正确运用，计算不准确，费了九牛二虎之力计算出错误的结果.数学每一步运算都以定义、定理、公式、法则为依据，因此，正确理解概念、准确掌握公式、定理、法则是准确、迅速、灵活运算的根本保证，提高学生的运算能力应是数学复习中一项长抓不懈的工作.

3.设计问题串展示概念表征的多层性

数学概念的层级性决定数学概念表征的多层性、多样性，同一个概念可以从符号、文字、图形等方面认识它，这是学生理解概念的一个困难，其次，学生不能熟练地在不同表征之间将概念转换，在新情境中识别概念的表征是学生不能正确解题的一个重要原因.因此，高三数学复习教师要帮助学生站在数学学科整体高度上再次经历概念的形成过程，了解概念的产生背景，体验数学化的方法，多角度、多层次设计数学问题、数学活动分析、理解概念的表征，提高抽象概括能力、数学表达能力，帮助学生构建概念系统，清除理解上的盲点、难点，优化知识结构，领悟数学概念中蕴含的数学思想、方法，建立从概念到解题方法的自然链接，在概念辨析中深化认识，强化概念本质的理解与应用意识的培养，使数学问题解决过程变为学生玩概念、品概念、用概念的活动，提高学生分析问题、解决问题的能力，坚决摒弃一个概念、多项注意的抽象讲解式的复习模式.

如在复习平面向量的基本定理时笔者设计如下问题（取得较好的复习效果）：

问题1：平面向量基本定理是什么（多种表示）？如何证明？基本定理的核心是什么？作用是什么？在解题过程中什么样的两个向量最有资格作为基底向量？如何求常数λ、μ（数形结合、方程思想）？

通过问题经历概念的形成过程，理解概念的内涵、外延等，深化概念认识，通过概念不同表征之间的联系，学习数学的表达，体验数学的发展，领悟数学的应用.

创设情境，应用概念，体会思想方法，深化理解概念.

变化条件，设置情境，发展概念，引领学生深化概念的理解及应用，升华学生的思维，提高理解能力.

问题4：在平面直角坐标系中，O是坐标原点，两定点A、B满足则点集|λ|+|μ|≤1，λ，μ∈R｝所表示的区域的面积是（ ）.

设置新的情境，强化抽象、概括、阅读、理解、应用意识，在不同背景下应用概念，形成自觉运用概念的思维定势，建立从概念到解题方法的自然链接，在概念的应用过程中自然、流畅地解决问题.

创设情境，增加内涵，增大思维量，一题多解，提升学生的解题能力.

通过以上问题的解决，能够达到将平面向量基本定理这一基础知识放在不同表征系统中，在给定的表征系统中能够熟悉地识别，能够熟练地从一个表征系统转化到另一个表征系统.

1.章建跃.中学数学课改的十个论题［J］.中学数学教学参考（上），2010（3~5）.F