滑动轴承等效刚度阻尼的计算分析方法
熊 涛,姚廷强,黄雅成
(昆明理工大学机电工程学院,云南 昆明650500)
0 引言
滑动轴承广泛应用于冷轧机、金属切削、水轮发电机、水泥磨机等旋转机械中,滑动轴承的支承性能对系统稳定运行至关重要。旋转机械转速越来越高,由滑动轴承失效引起的系统故障也越来越频繁。高速稳定已成为旋转机械系统目前的研究热点,其难点就在于滑动轴承刚度和阻尼的计算,同时由于滑动轴承油膜压力轴向分布不均,这也导致了滑动轴承的刚度阻尼特性在轴向各个截面并不相同,很有必要对滑动轴承刚度阻尼轴向变化情况进行分析研究,但目前的滑动轴承研究中很少涉及。
Guo ZL等[1]将油膜简化为半周油膜压力,首次运用CFD建立了滑动轴承求解模型,指出运用CFD可以求解轴承的流动特性,CFD结果与雷诺方程比较,只有在动力特性系数方面有较大的差别,而其余特性吻合较好。孙丹、张楚[2-3]等证明了运用两相流及动网格理论计算滑动轴承的刚度阻尼值与实际情况比较接近。Changhu Xing等[4]运用三维流体分析软件FLUENT对液体动静压轴承进行仿真分析,得出了比较可靠的润滑油膜无量纲阻尼系数的关系曲线。Gertzos K P[5]证实了纳维-斯托克斯方程在表征复杂求解域流体流动形态方面可弥补雷诺方程的不足,并引入了可动边界的概念。侯志泉[6]提出了基于N-S方程并结合动网格计算轴承刚度阻尼新方法并用实验证明了此方法的可靠性和可行性,但没有考虑轴承径向刚度阻尼在不同轴向位置处的变化规律。将动网格方法运用到轴承径向刚度阻尼的计算中,通过结合FLUENT瞬态和稳态计算的方式,运用动网格模型对滑动轴承进行等效刚度阻尼参数计算,对比分析多截面、多工况下等效刚度阻尼变化情况并得出其变化规律,为转子系统滑动轴承等效结合部参数的研究提供了一种方法。
1 刚度阻尼的计算方法
轴颈受外力作用偏离静平衡位置,并在静平衡位置附近做位移运动,因其位移和幅值很小,可将油膜等效为弹簧刚度阻尼[6],油膜的刚度阻尼特性反映了轴颈受外部载荷作用下振动位移和振动速度与油膜力之间的内在联系。
油膜力变化与位移扰动和速度扰动的关系为:

ΔFx、ΔFy为油膜力变化;kxx、kyy为直接刚度;kxy、kyx为交叉刚度;cxx、cyy为直接阻尼,cxy、cyx为交叉阻尼;Δx、Δy 表示位移扰动;x′、y′ 为速度扰动。
采用差分法对式(1)进行简化后,油膜的刚度阻尼计算公式为:

ΔFvij为速度扰动引起的油膜力变化;ΔFsij为位移扰动引起的油膜力变化。
2 滑动轴承建模
以汽轮发电机用液体动压滑动轴承SKF PWM8090100为研究对象。轴承内径为80mm,外径为90mm,宽度为100mm,节流口径为8mm,轴瓦厚度为5mm,轴承半径间隙为50μm。润滑油采用主轴2号油,动力黏度是0.003 85Pas,密度是810kg/m3。润滑油从水平面左右两端口进入轴承间隙内,出口形式采用的是端泄,即从前后两端面出油。
由于在FLUENT中进行动网格计算对模型网格要求比较高。所以,采用六面体结构化网格进行网格划分。综合考虑各方面因素进行几组网格划分,对比计算结果后,采用结果最理想的方式:在非承压油膜区设置100个节点,主要油膜承压区设置150个节点,油膜径向设置50个节点,油膜轴向设置300个节点,总共生成495 670个六面体结构网格,网格划分结果如图1所示。
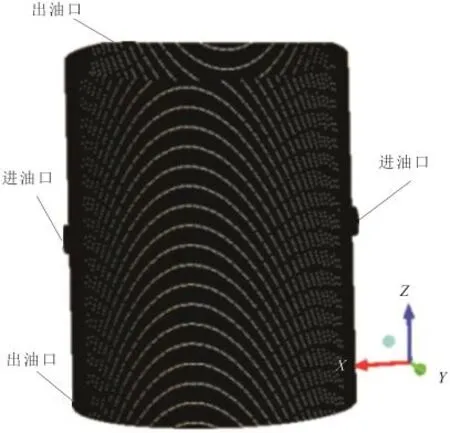
图1 模型网格划分
3 滑动轴承刚度阻尼计算
轴颈处于平衡位置时,外界对轴颈的位移扰动和速度扰动的范围不同,油膜力的变化将会有很大的差异。轴颈位移扰动和速度扰动取值范围的确定对刚度阻尼计算非常重要。利用FLUENT的稳态计算和瞬态计算,通过计算平衡点稳态油膜力和受到扰动后的瞬态油膜力,得出位移扰动和速度扰动对油膜力的影响,从而计算出油膜刚度阻尼的位移扰动和速度扰动的取值范围。
3.1 刚度阻尼扰动范围确定
调用FULENT用户自定义程序控制转子的位移扰动和速度扰动,使模型从平衡位置沿-y方向运动,来确定不同位移扰动和速度扰动下,x方向和y方向的油膜力,并与稳态油膜力计算结果进行对比,得出油膜力的变化。

图2 速度扰动对油膜力的影响
速度扰动下油膜力x方向分力如图2a所示,所有扰动速度下油膜力x方向分力最大差值均低于10.3%,平均差值均低于9.05%,扰动速度对油膜力x方向分力影响并不明显。图2b为速度扰动下油膜力y方向分力,扰动速度为12.5μm/s时,油膜力y方向分力最大差值为7.37%,平均差值为4.81%,扰动速度为125μm/s时,油膜力y方向最大差值为11.9%,平均差值为5.7%。扰动速度为12.5mm/s时,油膜力y方向最大差值为28.4%,平均差值为20.5%。从图2可以看出,在同一速度扰动下,随着偏心率的增大,油膜力x,y方向的分力均增大,即油膜力增大;在同一偏心率下,速度扰动越大,油膜力越大。
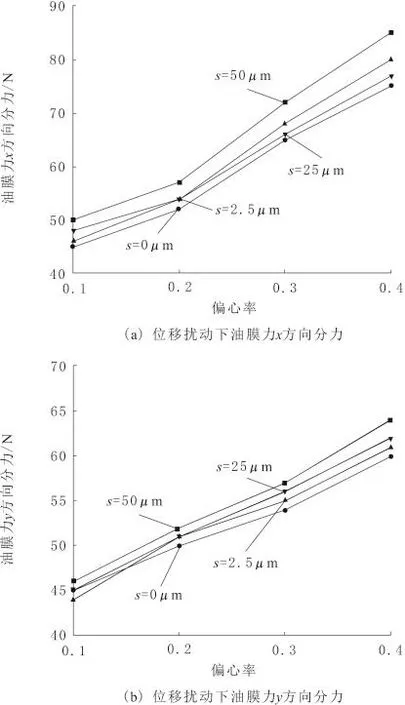
图3 位移扰动对油膜力的影响
位移扰动下油膜力x方向分力如图3a所示,s=2.5μm,油膜力x方向分力最大差值为8%,平均差值为4.61%。s=25μm时,油膜力x方向分力最大差值为8%,平均差值为6.82%。s=50μm时,油膜力x方向分力最大差值为14%,平均差值为12.27%。图3b为位移扰动下油膜力y方向分力,油膜力y方向分力受位移扰动的影响不明显,油膜力y方向分力最大差值均小于6.67%,平均值均小于4.13%。从图3可以看出,在同一位移扰动下,随着偏心率的增大,油膜力也相应增大;在同一偏心率下,位移扰动越大,油膜力就越大,与图2得出的规律相类似。
3.2 刚度阻尼计算
由图2和图3可知,当扰动速度v≤125μm/s,扰动位移s≤125μm,扰动前后油膜力变化较小,因此进行刚度计算时将扰动速度设定为20μm/s,位移扰动设定为10μm;当扰动v≥12.5mm/s,油膜力变化较大,因此进行阻尼计算时将扰动速度设定为20mm/s,位移扰动设定为10μm。
轴颈的转速为7 000r/min,进油的压力为1 MPa。在FULENT中进行求解,可以得到扰动前后油膜力,并带入式(2)进行计算得到刚度阻尼参数,如表1所示。

表1 轴颈左端截面刚度阻尼参数表 N/μm
4 等效刚度阻尼参数变化规律
4.1 轴向位置对等效刚度阻尼参数的影响
将滑动轴承沿轴向等分为10个截面,采用上述方法,对轴向各截面刚度阻尼参数分别进行计算,得出刚度阻尼沿轴向的变化情况如图4所示。
图4a为轴向位置对直接刚度的影响。kxx和kyy沿轴向的变化规律为中间较大,两端较小,与油膜力沿轴向的分布规律类似[7]。kxx和kyy在多截面位置分布不均,这是引起转子弯扭变形的重要因素,也说明了研究刚度阻尼沿轴颈方向的变化规律对系统稳定性非常重要。图4b为轴向位置对交叉刚度的影响。kxy和kyx的数值不等,即存在交叉刚度,交叉刚度从轴颈中心向轴颈两端逐渐减小。当轴承通过交叉刚度施加给轴颈的切向力大于轴承施加给轴颈的阻尼力时,轴承对轴颈产生沿油膜涡动方向的切向力,导致油膜涡动加剧,引发滑动轴承自激振动,引起轴承失效及转子系统失稳。图4c为轴向位置对直接阻尼的影响,其变化规律与直接刚度类似,轴颈中心截面处达到其最大值,而且其幅值远大于交叉刚度。图4d为轴向位置对交叉阻尼的影响,cxy和cyx从轴颈中心向两端分别沿正负方向减小,其中cyx为负阻尼,负阻尼与阻尼的作用相反[8],将导致系统振动的振幅逐渐增大,最终引起轴承失稳。
根据油膜等效刚度阻尼的定义,刚度阻尼分别表示油膜力和振动位移及振动速度的关系,因此当振动位移及振动速度为常数时,等效刚度阻尼沿轴向的变化应当和油膜力沿轴向的分布规律大致相同,这与图4得出的结论相符。刚度阻尼参数沿轴向的分布虽然存在交叉刚度和负阻尼的不利因素,但其值较小,所以滑动轴承整体仍是稳定的。

图4 轴向位置对刚度阻尼的影响
4.2 转速对等效刚度阻尼参数的影响
在多种转速工况1 000r/min、3 000r/min、5 000r/min、7 000r/min、9 000r/min、11 000r/min下,对轴承左端截面等效刚度阻尼参数分别进行计算,得到其随转速的变化情况如图5所示。
图5a为转速对等效刚度的影响,kyy的变化较明显,kyy先随转速增大而增大,进入高速阶段后随转速增大而减小。kxx随转速在3~6N/μm之间波动变化,但波动幅值逐渐减小,其总体趋向平稳且略有下降。kxy随转速增大而增大,kyx虽然随转速波动变化,但总体呈上升的趋势,即交叉刚度变大,油膜稳定性逐渐降低。图5b为转速对等效阻尼的影响,直接阻尼cxx和cyy随着转速增加呈下降的趋势,油膜的支承性能下降。kxy先随转速增大而减小,然后随转速增大,最后趋近于1N·s/mm左右。cyx变化规律与cxy相反,最后趋近于-5N·s/mm左右。
滑动轴承等效刚度阻尼参数随转速的变化规律较复杂,轴承进入高速阶段后,随转速增加,直接刚度略微降低,交叉刚度逐渐增大,直接阻尼逐渐下降,交叉阻尼较为稳定,与雷诺方程计算的变化趋势相近[9],说明随着转速增加,滑动轴承的稳定性降低,这也与工程实际相符。

图5 转速对等效刚度及等效阻尼的影响
5 结束语
利用FLUENT用户自定义程序确定了合适的速度扰动和位移扰动范围,采用动网格模型进行求解,并将求解结果带入N-S方程,计算了多截面变工况下滑动轴承等效刚度阻尼参数。
对比分析了多个截面位置的滑动轴承的刚度阻尼参数,得出滑动轴承的刚度阻尼沿轴向的分布规律为沿轴颈中心向两端逐渐减小,为获得更精确的滑动轴承等效油膜支承,提供了研究思路和数据参考。转速增加,轴承刚度各阻尼参数变化非常明显,计算多工况下滑动轴承等效结合部参数时必须考虑这一影响因素。分析滑动轴承等效刚度阻尼随转速的变化规律,为进一步研究滑动轴承-转子系统动力学性能提供了研究基础和依据。
[1] Guo Z L,Hirano T,Gordon Kirk R.Application of CFD analysis for rotating machinery-Part I:hyd-Rostatic bearings and squeeze film damper[J].Jou-Rnal of Engineering for Gas Turbines and Pow-Er,2005,127(2):445-451.
[2] 孙丹,张楚,郭瑞,等.基于两相流理论滑动轴承动力特性求解[J].航空动力学报,2012,27(12):2821-2827.
[3] 张楚,杨建刚,郭瑞,等.基于两相流理论的滑动轴承流场计算分析.中国电机工程学报[J],2010,30(29):80-84.
[4] Chang H X,Minel J Braun,Hongmin Li.Damp-Ing and added mass coefficients for a squeezeFilm damper using the full 3-D Navier-StokesEquation[J].TribologyInternational,2010,43:654-666.
[5] Gertzos,Nikola K P.CFD analysis of journal be-aring hydrodynamic lubrication by Bingham lu-bricant[J].TribologyInternational,2008,41(12):1190-1204.
[6] 侯志泉.基于CFD动网格方法的液体静压主轴回转精度机理研究[D].长沙:湖南大学,2013.
[7] 董勋.润滑理论[M].上海:上海交通大学出版社,2001.
[8] 徐龙祥.高速旋转机械轴系动力学设计[M].北京:国防工业出版社,1994.
[9] Ghosh M K,Majumdar B C,Rao J S.Steady-state and dynamic behaviour of multi-re-cess hybrid oil journal bearing[J].Journal of Mechanical Engineering Scinence,1979,21(5):345-351.

