一种基于计算机视觉的无人机实时三维重建方法

张臻炜，赵 勇，布树辉

（西北工业大学航空学院，陕西 西安710072）

0 引言

基于计算机视觉的SLAM，即同时定位与地图构建，由于其重要的理论与应用价值，一直以来都是学者研究的热点。相比较传统的测绘技术，视觉SLAM的三维地图重建，在对传感器依赖比较少的前提下，最大限度利用获取到的图像信息，同时高效的信息处理决定了其能够实时重建出三维环境。然而，图像信息采集过程中的噪声干扰和图像处理带来的大计算量一直以来限制该技术应用于实践中。引入图优化的思想，来降低传感器噪声累积对整个系统的影响。同时由于RGB-D传感器能同时提供颜色和深度信息的图像，使得稠密重建的计算复杂度大大降低，提高系统实时运行的能力。

1 视觉SLAM

1.1 运动估计

对于相机采集到的数据，系统用事先测定的相机标定数据进行图像去畸变处理，得到去畸变后的图像［1］。通过跟踪由相邻的几个关键帧组成的局部地图上的特征点来估计每个新帧的运动状态。提取Fast-Corner或者ORB特征用于描述特征点。并且采用运动模型，由于帧率比较高，相邻帧的差别（时间、空间）不是很大，可以把前一帧的运动状态当做该帧运动的初始估计。为了提高系统的鲁棒性，保留像素深度的不确定性，即引入高斯分布的深度概念，一个像素有深度值的同时还有深度的方差值，并假设其服从高斯分布。然后，通过迭代计算最小化光度和深度残差函数（通过地图点和新的帧上的特征点匹配而得到的）来获取运动估计。提出的方法应用金字塔模型来增强系统的鲁棒性，尤其是针对高速运动造成的图像模糊情况。其中跟踪的质量是通过计算成功匹配的数量和最小化的残差值来定义的，同时用于检测跟踪丢失和判断是否要建立新的关键帧。由于在实验中不可避免地会出现跟踪丢失的情况，因此一旦出现“丢帧”，就必须实施基于关键帧匹配的“重定位”，以便估计之前的运动参数。

1.2 坐标定义、转换与相机投影

相机的姿态通常用矩阵H来表示为：

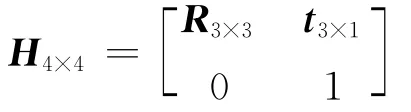
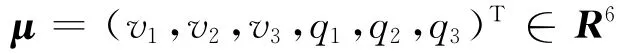
这里的旋转矩阵R是3×3的正交阵，R∈SO（3），平移量t是3×1的向量，t∈R3。这个变换矩阵H是过参数的，因为它有12个参数，但是只有6个自由度。因此用向量μ来表示为［2］：v1，v2，v3为平移量；q1，q2，q3为旋转。μ 与H的相互转化为H＝exp（μ）。对于一个世界坐标系下的点p＝（X，Y，Z，l）T，可以将其转化到相机坐标系下为p′＝R［X，Y，Z］T＋t＝HR＝exp（μ）P。将相机坐标系下的点Pc＝（Xc，Yc，Zc，l）T投影到像平面上p＝（x，y，d）T，其中（x，y）T是像素坐标，d是像素深度。标准的针孔相机模型用来表示投影变换为：

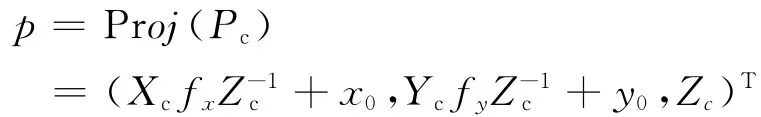
fx，fy是焦距；x0，y0是像平面的中心。与之类似，从像平面上往相机坐标系的映射为反投影。

1.3 运动先验与运动更新

系统可以采用滤波器或者其他传感器（如IMU）来获得运动量的“经验值”。然后针对快速运动，利用这个“经验值”来增强系统鲁棒性和判断是否需要金字塔模型。如果前一帧跟踪效果好，那么就可以用前一帧的运动量作为下一帧的“经验值”，这样做有利于后续的运动优化。

当地图初始化完成后，就将地图上的点投影到当前帧中。然后去寻找最佳的Fast-Corner匹配［3］，用于计算残差。为了限制全局地图的复杂度，只投影那些由关键帧组成的局部地图（子地图）上的点。如果地图点满足以下要求就会被丢弃。①算出地图点在该帧的投影P′，如果P′不在该帧图像范围内就舍弃它；②计算该点与相邻的特征点的ORB距离d，找一个最佳匹配。给距离d设定一个阈值，若超过这个阈值就舍弃它；接着，如果系统获得了一些三维地图点和RGB-D图像的像素点的匹配关系，那么就能估计相机的姿态μ。为了充分利用像素坐标值和深度信息，采用一种鲁棒的残差函数来估计运动位姿，残差为：

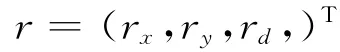
被定义为地图点计算值和预测值的误差为：

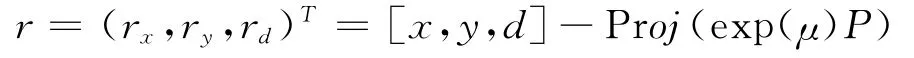
理想情况下，残差值为零。然而，由于信息采集的噪声，残差是基于概率模型p（r1μ）分布的。然后通过最小加权残差函数来估计相机位姿μ＝。这里的加权误差项是由误差的参考值动态确定的。加权项wi用来降低大残差的影响。

对于估计相机移动而言，以上的处理已经足够了。但其实还可以通过点的投影残差来获得更高的精度。这时候一些对应点的深度值可能无效，那么这些点的权重就很小，甚至被忽略。尽管它的深度方差很大，仍然使用它的RGB值。而这适用于纹理丰富而深度信息很弱的场合。同时应用金字塔模型来避免由于快速运动导致的“丢帧”现象。当用运动模型获知之前一帧的“运动幅度很大”时，就先在低图片的分辨率上去做跟踪：即在底层的金字塔上，在只有较少的几个特征点，且较大的搜索半径下去估计位姿μ。然后缩小半径，提高分辨率，增加匹配的特征点个数，以获得更加精确地位姿。

1.4 失败恢复

尽管已经付出最大的努力来让整个系统尽可能地鲁棒，在某些时候跟踪仍然还是会失败。用成功匹配的点的数量和最小化的残差函数值来估计追踪的质量。如果跟踪系统没有获得足够多的匹配或者平均的加权半径超过了允许的范围，那么就将跟踪定义为失败［5］。一旦跟踪失败，重定位线程就会将开启，用来冲失败中恢复整个系统：选择一些候选的关键帧，然后尝试去寻找当前帧上的特征点与这些关键帧上的点的匹配关系。然后基于这些三维对应点，用SANSAC算法算出一个位姿的估计值。如果对应点足够的多，那么就用这个估计值来继续执行后续的程序。

2 关键帧处理、图优化与数据融合

2.1 关键帧的建立

为了更好地建立全局地图，引入关键帧的概念。关键帧的设立是由于其具有的位姿相对于前一个关键帧变化较大，其探测到的三维环境信息相比较于之前的关键帧有较大不同，因此将其设为一个标尺，用于扩展全局地图和检测后续的帧是否有较大的位姿变化：通过检测到的特征点进行两帧之间的特征匹配，然后判断是否创建新的关键帧。这里采用一种新的衡量两帧之间相似度的标准：用Relij来表示第i帧与第j帧的相似度为：

μij表示第i帧和第j帧的相对位姿；E（di）定义为第i个关键帧的平均深度。W 是表示权重的对角矩阵。当关键帧间的Relij值比较小时，意味着产生了比较多的新的信息，也就是说这时候有必要增加一个新的关键帧了。此外，一个新的关键帧必须符合的要求是，①为了确保当前的姿态估计是基于一个良好的重定位的，一个新的关键帧应该在前一个全局的重定位之后过15帧以上在添加；②跟踪的精度应该足够好，最后被舍弃特征点对应的数目要少于50对。

获取当前的位姿变化量之后，除了进行前面是否添加关键帧的判断以外，还将该帧新检测到的特征点同过相机内参和刚才获得的位姿参数反投影回三维空间，加入全局地图中，就这样一步步扩展全局地图。

2.2 图优化

由于相机的限制，采集到的图像信息是包含着噪声的（无人机对于自身的定位是依赖于所检测到的图片信息，而且这个误差还会累积，最终导致了三维重建的结果由于误差太大失去实用价值），因此系统需要对生成的地图进行优化校准，采用图优化的思想［4］如图1所示，先进行局部的Bundle校准，先寻找相近的几个关键帧先进行小规模的Bundle校准，等全部的地图构建完成后再进行一次全局的校准，校准的目的是为了减小累积噪声的影响。引入图优化来减小来自传感器的误差对最终结果的影响，矫正每一步的位姿，以实现全局优化为：

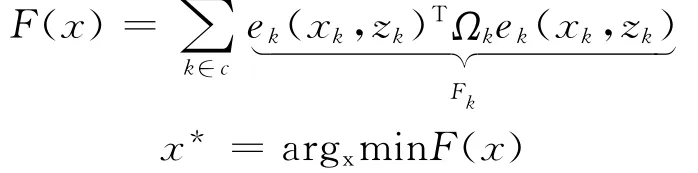
xk为前面定义的节点（也可以理解为状态）；zk为边（也可以理解为约束）；ek为这些节点满足约束的状态（如果没有噪声及ek＝0）；Ωk为引入的信息矩阵及约束的置信度，如果误差大则它对应的置信度就小。定义完变量之后，接下来要做的就是使整个误差函数降到最小，以达到全局最优的目的［6］。将地图点的三维位置和无人机的位姿定义为节点，将从图像到地图点的投影关系和相邻两帧之间的SE（3）的变化定义为边，信息矩阵包含两方面，地图点的被关键帧观测次数和图像中点的灰度梯度。

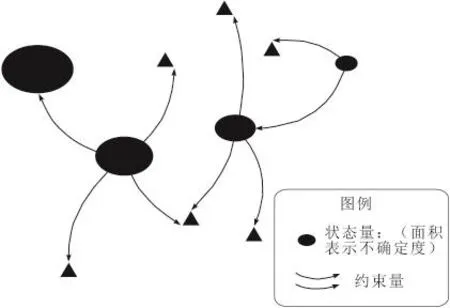
图1 图优化示意

2.3 数据融合

在产生全局地图点的时候，如果仅由当前帧与当前关键帧通过三角化反投影回三维空间产生，会降低程序的鲁棒性（往往也不精确）。因此，需要将三角化产生的地图点投影到几个相邻的关键帧上（前提是这个地图点在这些关键帧的可见范围内），在小范围内进行特征匹配，然后再重新反投影回三维空间，最后对多个值进行加权平均，得到一个更加合理的地图点。

3 实验结果

以下将展示重建的结果，包括实时和离线数据的测试结果，并与当前一些主流的视觉SLAM方法作比较。以下所有的测试都在mint 17（基于ubuntu14.04，64bit）上进行，8GRAM，不用 GPU，主频3.50GHz。说明：图像数据采集自西北工业大学友谊校区、航空楼A-412民航工程实验室。以下是实验截图，包含实时全局点云图（白色的点绘制三维地图；红色的相框表示当前的实时相机的位姿；蓝色的相框代表系统创建的关键帧；青色的线代表关键帧之间的约束），实时深度估计图（从红到蓝表示由近到远），实时深度方差图（从红到蓝表示方差由小到大）（注：以上说明于彩色版面图像可见，黑白版面无法识别）和原始图像数据（1 920×1 024，灰度图）。

图2 原始图像、深度、深度方差

图3 重建半稠密点云图

接下来将通过与其他主流SLAM方法比较来评估性能与数据指标如表1所示。通过比较可以发现，

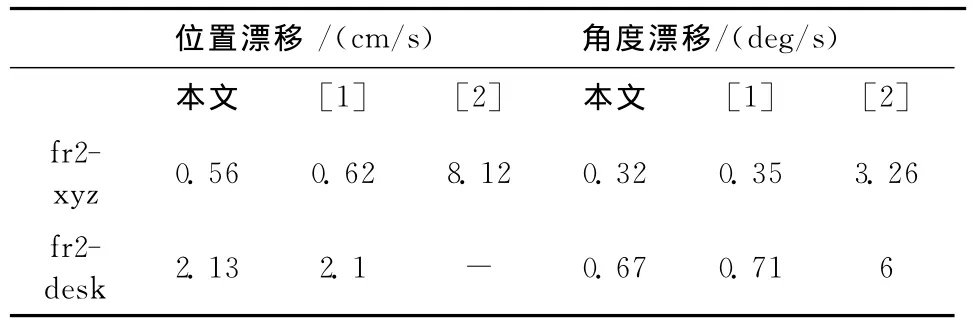
表1 RGB-D基准 测试结果比较

无论是位置漂移量、角度漂移量还是绝对误差都较低，同时系统实验精度依然能够达到实用标准，而且能够直接在CPU上运行，不用要求GPU。

图4 ICL公开测试数据

4 结束语

提出一种基于计算机视觉的无人机实时三维重建方法，通过算法实现无人飞行器在未知环境下实时定位和环境感知，针对传感器带来的累积噪声，采用图优化的思想，达到全局最优的效果。通过当前帧与地图点特征点匹配，得到当前相机的相对位姿。实验结果表明本方法在保证重建精度的前提下，能够实现实时运行。

［1］ Zhenyou Zhang.A flexible new techniquefor camera calibration［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（11），1330-1334.

［2］ Selig J M.Lie groups and lie algebras in robotics［C］／／Computational Noncommutative Algebra and Applications.Springer，2004.

［3］ Rosten E，Drummond T.Machine learning for highspeed corner detection［J］.Computer Vision-ECCV2006.Springer，2006.

［4］ Kummerle R，Grisetti G，Strasdat H，et.al.G2o：A general framework for graph optimization［C］／／IEEE International Conference on Robotics ＆ Automation，2011：3607-3613.

［5］ Endres F，Hess J，Sturm J，et.al.3-D maping with an RGB-D cameras［J］.IEEE Transaction on Robotics，2014，30（1）：177-187.

［6］ Guivant J E，Nebot E M.Optimization of the simultaneous localization and map-building algorithm for realtimeimplementation［J］.Robotics ＆ Automation IEEE Transactions on，2001，17（3）：242-257.