一种挖掘机动臂板厚的优化设计方法
张海峰,吴盛彬,刘孝保
(1.昆明理工大学机电工程学院,云南 昆明650500;2.贵州詹阳动力重工有限公司,贵州 贵阳550006)
0 引言
液压挖掘机动臂是工作装置的主要受力部件。在施工过程中,动臂可能因板厚设计过薄而会出现开裂甚至断裂的现象,影响挖掘机正常的工作和使用。因此动臂的设计优劣,关系着挖掘机的工作效率和使用寿命[1]。
挖掘机动臂为左右对称封闭的中空箱体焊接结构,其为复杂的板壳结构,在对其进行设计时难以利用板壳理论求解,而国内外涉及板厚设计的研究对经验依赖程度较高,且多为冗余设计[2-3]。目前国内关于板厚度优化的研究较少,且多需要迭代运算,计算较为复杂[4-5]。
为此,提出了一种挖掘机动臂板厚的优化设计方法。首先,根据有限元理论和板壳理论建立了板壳应变与板厚优化设计的数学模型。然后,提出了基于ANSYS的优化设计实现方法。最后,利用某挖掘机的动臂板厚优化实例进行验证,验证结果表明该优化设计方法的可行性和有效性。
1 动臂的优化设计
复杂板结构难以利用板壳理论直接计算,为此,可将有限元理论和板壳理论结合建立应变、位移和板厚之间的关系模型。
该优化方法以板厚h为设计变量,以板件在确定结构确定边界条件下的应变ε为优化目标,其优化模型为:
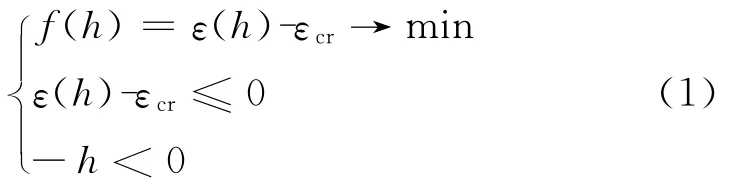
ε(h)为最大应变ε为板厚h的函数;εcr为设计要求的最大应变。
根据材料力学,式(1)的优化解可进一步简化为:当ε(h)=εcr时的临界板厚为hcr,结合有限元理论与板壳理论建立应变ε与板厚h之间的数学模型,其最优解为h*=hcr。
1.1 厚度优化设计理论推导
根据薄板近似理论假定,板壳单元在物理方程中略去应力分量σz,则出单元应力σ与节点位移u的关系式为[6]:
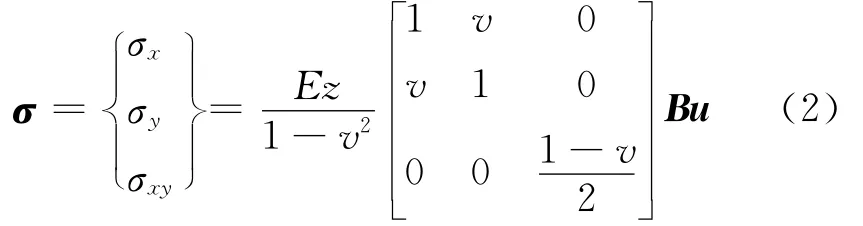
E为弹性模量,v为泊松比,B为应变矩阵,u为节点位移向量,z为点到板中性面的距离[7]。为计算方便,记T为:

根据板壳理论,应力分量σx、σy和τxy沿薄板的厚度方向的最大值在平板表面,即z=h/2。因此,由式(2)可知板表面的应力为:

根据弹性力学中应力与应变的关系[7]:

ε为应变;D为弹性矩阵。
将式(5)带入式(4)可得到:

根据有限元理论,节点位移向量u与节点载荷F有如下关系:

根据有限元理论和材料力学,平面载荷的刚度矩阵K为:

Ku表示壳厚度为单位1的刚度矩阵[8]。
根据有限元理论可知,对完全约束的结构,Ku为可逆矩阵。因此,将式(8)带入式(6)可得:
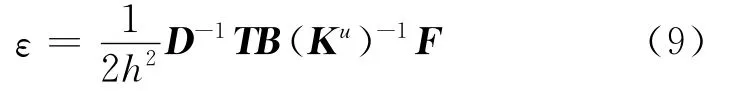
式(9)表明了ε和h的关系,但无法用其进行计算。因此,假设板壳厚度为h=h1时,板壳的应变ε1为:
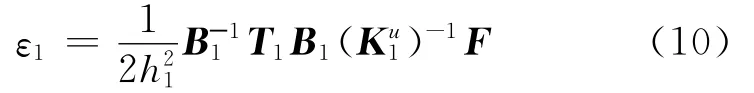
当板壳厚度h=hcr时,板壳的应变εcr为:
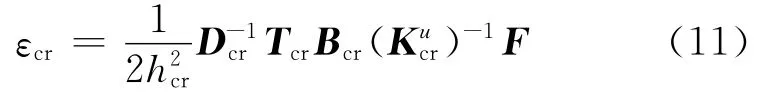
因为材料模型,网格划分和单元类型均相同,所以有T1=Tcr、B1=Bcr、D1=Dcr和=,将式(10)和式(11)相除得:

具有相同物理意义的标量ε1和εcr也同样满足上式关系[9]。因此,优化厚度hcr可表示为:

实际工程中,通过安全系数s来提高设计的可靠性,考虑安全系数后设计厚度可表示为:

1.2 厚度优化设计实现方法
由式(14)知,求板壳厚度hcr,需先获得板厚为h1时的应变ε1。对于复杂的板壳结构,利用板壳理论求解应变ε1非常困难,因此借助有限元软件求解。为此,提出了基于ANSYS的板厚度优化设计实现方法。
首先,利用ANSYS软件计算厚度h1为时的应变ε1。然后,根据设计要求计算最大应变εcr和安全系数s,通过式(14)计算,获得最优设计厚度hcr。最后,通过ANSYS进行验证。具体过程如图1所示。

图1 基于ANSYS的板厚度优化实现方法
2 实例验证
以某品牌小型反铲挖掘机例,取安全系数s的值为1.5。其动臂模型如图2所示。
本型号挖掘机动臂所用材料为Q 345,其屈服强度为345MPa。通过计算得到最大变应为εcr≤0.00173。故优化目标为:εcr≤0.00115。
首先对动臂进行灵敏度分析以确定对应变最灵敏的板件,并对其进行厚度优化设计。结果如图3所示。
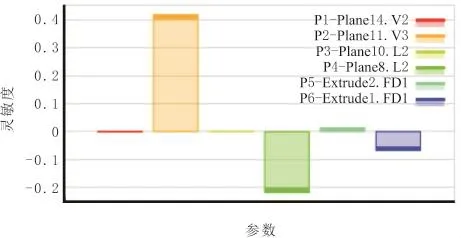
图3 各参数与应变的灵敏度
图中P1为前上盖板厚,P2为前下盖板厚,P3为后下盖板厚,P4为后上盖板厚,P5为前侧板厚,P6为后侧板厚。从图中可以看出前下盖板厚对应力最为敏感,因此对其进行厚度优化。动臂前端下盖板厚度为其初始厚度h1=10mm时,在ANSYS中设置最大挖掘力工况,将动臂1、2处施加完全约束,动臂3、4处施加轴承力,具体如表1所示。

表1 动臂3点和4点所受轴承力 kN
动臂前端下盖板最大应变εt=0.00137。如图4所示。
其最大应变的安全系数约为1.26,小于1.5。因此对其进行优化改进。根据最大应变,取s=1.5,代入式(14),计算前端下盖板的优化厚度hcr=10.90mm。

图4 动臂前端下盖板最大变应
根据式(14),得到优化板厚为10.90mm。取整后为板厚ht=11mm,改变前端下盖板的厚度,进行验证,得出前下盖板的最大应变εt=0.00113,经计算,最大应变优化后前端下盖板的安全系数为1.53大于1.5,满足设计要求。如图5所示。

图5 动臂前端下盖板最大变应
3 结束语
提出了一种挖掘机动臂板厚的优化设计方法。首先,根据有限元理论和板壳理论建立了板壳应变与板厚优化设计的数学模型。然后,提出了基于ANSYS的优化设计实现方法。最后,利用某挖掘机的动臂板厚优化实例进行验证,验证结果表明该优化设计方法的可行性和有效性。
[1] 李金晓,杨茹萍.液压挖掘机动臂的有限元分析 [J].建筑机械化,2009,30(11):59-62.
[2] Liu X B,Yin Z H .An optimized design method for thickness of shells with multi-holes based on finite element method theory[C]//2012 3rd International Conference on Advances in Materials and Manufacturing Processes(ICAMMP 2012),Beihai,2013.
[3] Pedersen P.On thickness and orientational design with orthotropic materials[J].Structural Optimization,1991,3(2):69-78.
[4] 杜群贵,迟永滨.通用结构优化设计系统的研究与实现[J].机械,2001,28(6):22-24.
[5] 兰凤崇,陈吉清.承载式车身覆盖件板厚优化及灵敏度分析[J].航空制造技术,2005(3):61-65.
[6] 赵均海,汪梦甫.弹性力学及有限元[M].武汉:武汉理工大学出版社,2008.
[7] 赵均海,汪梦甫.弹性力学及有限元[M].武汉:武汉理工大学出版,2008.
[8] Liu Xiaobao,Yin Zhihong.An optimized design method for thickness of shells with multi-holes based on finite element method theory[J].Advances Materials Research,2013(652):1478-1481.
[9] Long Y Q,Cen S,Long Z F.Advanced finite element method in structural engineering[M].Beijing:Tsinghua University Press,200.

