提升教师问题意识，促进主动发展的教学案例分析

王银珠　张新军

【摘 要】培养问题意识是学生主动探索的切入口，激发问题意识，形成自己的独立见解，真正改变学生的学习方式。数学教学中，数学问题意识是引发学生思维与探索活动的向导。教学中问题意识的构建要符合学生的认知起点，能引导学生探究数学发生的过程，寻找到数学的本质。

【关键词】问题意识；引领教学；活动中构建；提升学科能力

普通高中新课程《数学课程标准》的亮点是突出“过程性目标”。要学生“经历、体验、探索”。培养问题意识正是让学生主动探索的切入口，从而激发问题意识，形成自己的独立见解，真正改变学生的学习方式。同时新的课堂教学突显“问题引领教学活动”的认知。问题成为教学过程的起点，也是教学过程的指向，促进主动发展的课堂教学的着力点。

数学教学中，数学问题意识是引发学生思维与探索活动的向导。有了问题意识，学生的好奇心才能激发；有了问题意识，学生的思维才开始启动；有了问题意识，学生的探索才真正有效；有了问题意识，学生的学习动力才能持续。然而问题意识的引发离不开教师对问题意识有效构建，只有教师教学的问题意识铺垫，才能有效划归为学生的问题意识的构建。那种简单的“是不是”、“对不对”等没有思维含量的提问充斥课堂，只能弱化学生的智力。通过问题意识，才能把知识的逻辑结构与学生的思维过程有机的联系起来，使知识的逻辑结构转化为学生的认知结构，才能让学生有效发现数学的内在规律、认识、理解数学本质，并在活动中构建数学，真正完成问题意识的培养。

案例1.复数概念的引入

问题1：在遨游数字王国时，你还记得数的概念发生和发展的过程吗？在历尽几次“添加新数”之后，数集已经扩充到实数集。但是，由于负数在实数范围内不能开平方，所以代数运算在实数集内仍不能永远实施。有些代数方程的问题在实数范围无法解决或者解决的不够完美。例如，当b2-4ac<0时，实系数一元方程ax2+bx+c=0没有实数根；一元三次方程x3=1只有一个根，根的个数与方程的次数如此不一致。数的概念需要进一步发展。

实数集如何推广？

在新的数集里，怎样实施数的运算？

这里的问题情境表面上符合“数”的概念扩充过程，学生在过去的经验中熟悉了当“b2-4ac<0时，实系数一元方程ax2+bx+c=0没有实数根”这样的结论，现在要学生从中提出问题很难。这个情境与问题人为色彩严重，脱离了学生的认知起点，难以启动学生的思维。

问题2：16世纪，意大利数学家卡尔丹在讨论问题“将10分成两部分，使两者的乘积等于40”时，认为把答案写成5+和5-就可以满足要求：（5+）+（5-）=5+5=10.（5+）（5-）=5×5-×=25-（-15）=40.我们知道，在实数集内，一个正数有两个平方根，它们互为相反数，0的平方根是0，然而表示什么意义呢？你也许觉得這个问题有点可笑。因为任何实数的平方都是非负数，所以负数没有平方根，因此没有意义。尽管很长一段时间内，部分数学家都认为5+和5-这两个式子没有意义，是虚构的、想象的，但在解决许多问题时，使用类似于这样的式子却带来极大地方便。那么能作为数吗？它真的是无意义的、虚幻的吗？

这里以数学史上真实发生的故事作为情境，也展现了数学史上真实的问题，这个问题曾经困扰过许多数学家。今天，高中生同样会对这个看似荒谬但又难以否定的问题感兴趣。这个情境与问题符合学生的认知起点，所以学生问题意识的激发更需教师设计问题意识时依托性。

案例2.解三角形中——余弦定理

问题1.开门见山指出“在三角形中，已知两角及一边，或已知两边和其中一边的对角，可以利用‘正弦定理求其他的边和角。那么，已知两边及其夹角，怎样求出此角的对边呢？已知三边，又怎样求出它的三个角呢？”

这个问题是以复习引新式的模式提出来的，上承正弦定理，下启本节内容，在先概括正弦定理的基础上提出面临的问题，学生是否会马上提出解决这两个问题的另一个定理呢？他们的内心必然会呼应出余弦定理的诞生么？也许仍会构造直角三角形去完成此任务呢？

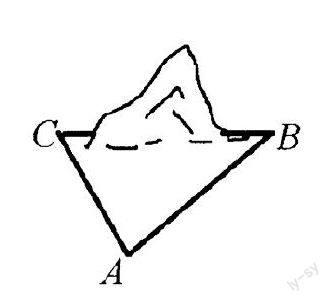
问题2.如图，某隧道施工队为了开凿一条三地隧道，需要测算隧道通过这座山的长度。工程技术员现在地面上选一适当的位置A，量出A到山脚B、C的距离，再利用经纬仪测出A对山脚BC的张角，最后通过计算求出山脚BC的长度。

这个问题是以问题情境式提出的，在学生脑海中很快就形成了一个认识冲突，即体现了数学教育联系实际，又很接近余弦定理的教学目标。

提出问题的出发点不同，对教学活动的导向作用也就不同。探究和证明余弦定理的过程既是本节的一个重点也是本节的难点。问题1及问题2都没有明确解题的目标。即解三角形的必要条件。特别值得一提的是，教材对正弦定理和余弦定理的讲解都用了向量法，可见向量的地位和作用多么的重要。并且运用向量法既可以克服几何论证中有时要添加辅助线但又难发现的缺陷，又可以带来用计算代替演绎论证的优越性，可使问题变得简洁明快、容易入手。但是学生处理问题的第一反应就是化为直角三角形，用勾股定理。向量法却很少提起，怎样让学生去想到0，再变形到，是不容易想到的。是技巧性太强？或是对向量的认识不足？教师在这里狠下功夫认真研究研究，怎样把学生扶上台阶，成为我们思考的问题。分析其问题之一是学生对向量的认识不足，学生在学习平面向量一章是有缺失，没有理解向量这一工具地位与重要作用。如何运用向量基底体现及坐标体系解决这个问题新课程是把他分解到另一章节中了。这里再次对教材的整体把握，新课程的螺旋式上升的理解对教师提出更高要求。问题之二是教师没有构建好学生的知识体系，当然也就无法完成学生的问题意识的构建。还是新课程的螺旋式上升在此处就有不合适之处呢？都值得我们的思考。

问题3.从三角形全等的判定定理可以知道，三角形的基本元素之间存在着一定的数量关系。例如三角形内角和定理揭示了三角形的三个内角间的数量关系，勾股定理揭示了直角三角形三边间的数量关系。

三角形基本元素间还存在着什么样的关系呢？

给出在三角形ABC中，存在着向量关系0，再变形到，怎样把向量关系转换为数量关系？经讨论利用向量的数量积可以讲向量关系转化为数量关系，在上式两边平方可以得到余弦定理；在上式两边同乘以向量AB垂直的向量，就是前面已学过的正弦定理。

这个问题开门见山，直入本节课的重点。这种接受性学习比发现性学习应该更注重反思过程，从定理的推导过程中你受到了什么的启发？用向量方法有什么认识？向量关系转化数量关系的途径有哪些？这样学生的问题意识的构建同样能完成。当然哪种问题意识的铺垫更能有助学生问题意识的培养仍是值得探讨的问题。

所以教师教学中问题意识的构建要符合学生的认知起点；能引导学生探究数学发生的过程，寻找到数学的本质；要有对教材的批判思想的问题意识；要有对教材的整体把握及新课程的螺旋式上升的理解的意识；要有问题意识的依托性、导向性、探究性。才能完成对学生问题意识的有效培养。

参考文献：

[1]旦智塔主编.甘肃省普通高中新课程研修100问.兰州：甘肃教育出版社，2012.5.

[2]付宜红，张炳意主编.普通高中课程建设与管理.北京：北京师范大学出版社，2010.7 .

[3]多元智能新视野：加德纳作品∕作者：（美）加德纳（Gardner，H.）著沈致隆译 北京：中国人民大学出版社，2008.03