进制转换教学设计
石元聆
摘 要: 进制转换的教学中有两个问题,一是学生对进制难以理解;二是学生对进制转换的方法死记硬背。针对高职学生的学习特点,用直观、类比的方法提出新的教学设计。这个教学设计经过一学期的教学实践,证明了能让高职学生很好地理解进制转换的内容,使这个教学难点成为一个易学知识点。
关键词: 高职院校; 进制; 进制转换; 教学设计
中图分类号:G712 文献标志码:A 文章编号:1006-8228(2015)11-96-02
Abstract: Teaching of number system conversion has two problems, one is students being difficult to understand the number system; second is students learning number system conversion by rote. For higher vocational students' learning characteristics, this paper puts forward a new teaching design with the method of intuition and analogy. After a semester of teaching practice, it is proved that this teaching design can make the higher vocational students to understand the content of number system conversion well, so that the teaching difficult point becomes an easy to learn knowledge.
Key words: higher vocational colleges; number system; number system conversion; instructional design
0 引言
在长期的计算机基础课程授课中发现,高职学生对进制转换的内容很难理解,本文结合历年的授课经验,对进制转换做一个新的教学设计。
1 用示例引入进制的概念
一般书上是这么描述的:进制就是数的表示方法。十进制就是用0-9十个数字来表示一个数,数字不够用的时候,就逢10进1。二进制就是用0-1二个数字来表示一个数,逢2进1。八进制就是用0-7八个数来表示一个数,逢8进1。十六进制就是用0-9 A-F这十六个数字来表示一个数,不够用时,逢16进1。但是,学生往往只是从语义上理解,不能很深刻的理解进制的含义。
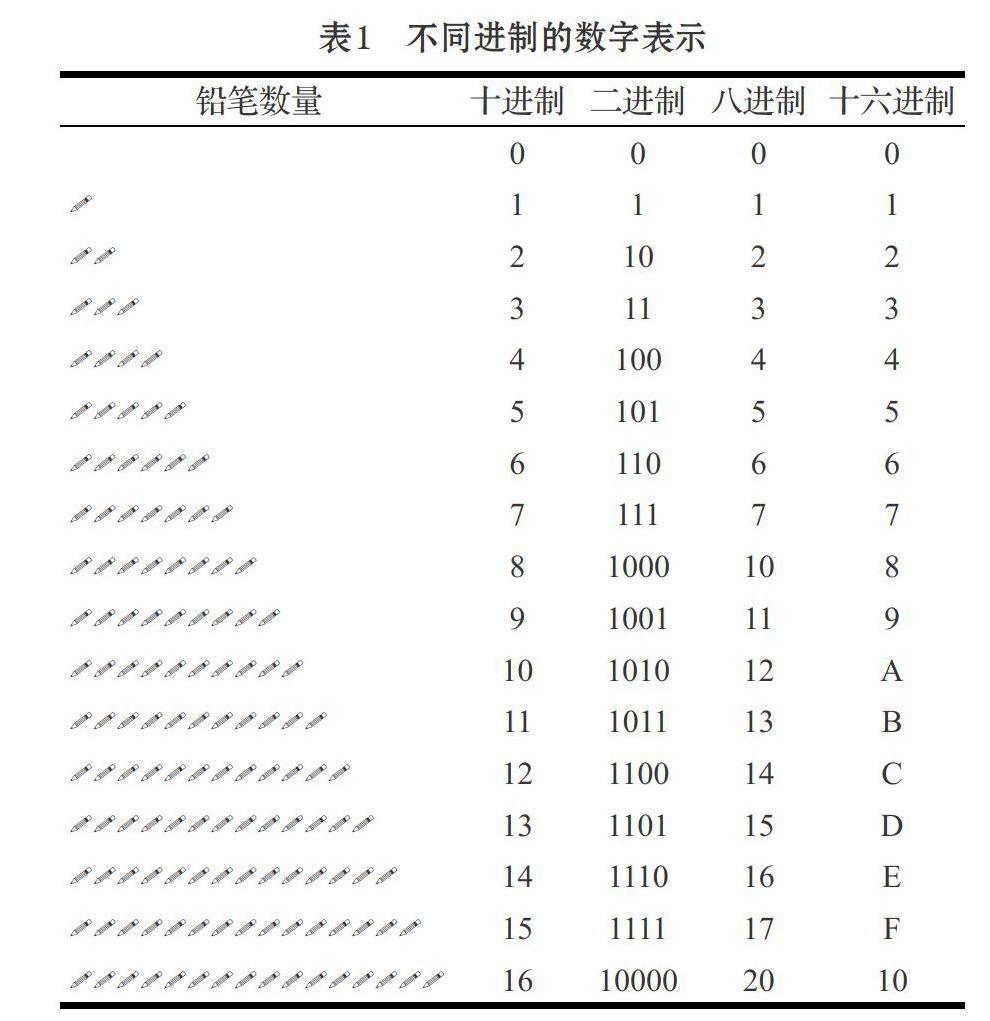
用例子来说明进制的概念,现在有0-16根铅笔,分别用十、二、八、十六进制来表示。一般老师领着学生画出表1,学生对进制的概念都能理解了。
2 进制转换
2.1 二进制和十进制之间的转换
二进制转换成十进制,一般书上是这么描述的:按位权展开。十进制转换成二进制直接给出算法,整数部分除2取余,小数部分乘2取整,但是为什么要这么做呢?没有说明,学生往往死记公式,学起来很枯燥。下面我们用直观的方法来进行推导运算。
2.1.1 二进制转换成十进制
根据表1,二进制是逢2进1,所以进到十位上的1,实际上就是2,也就是21,百位上的1,就是22,从表1也能得出这个结论。依次类推,小数后面第1位的1,就是2-1。比如:111.12=1*22+1*21+1*20+1*2-1=7.510。
2.1.2 十进制转换成二进制
⑴ 整数的转换
要把一个由0-9十个数字组成的十进制整数转换成一个只有0-1这两个数字组成的整数。我们知道,任何一个十进制数除以2,余数一定是0或1,比如5除2,余数是1,商是2;6除以2,余数是0,商是3。我们就用这个方法试试看。
2 [100] 0(余数)
除到商为0为止,最后得到的余数是最高位,最先得到的余数是最低位。10010=11001002,用2.1.1我们讲过的方法进行验证,准确无误。
⑵ 小数的转换
怎么把一个由0-9十个数字组成的十进制小数转换成一个只有0-1这二个数字组成的小数呢?我们知道任何一个十进制小数,比如0.99999,乘以2,它的整数是1,那我们再试几个十进制小数,乘以2,发现整数部分不是0就是1。那我们就考虑用这种直观的方法实现。将小数部分乘以2,取整数,再用剩余的小数乘以2,取整数,乘到小数部分为0为止(注意:乘不尽时,按精度进行舍入),最先得到的数是高位(紧挨小数点后面),最后得到的整数是低位。
下面我们就用这种方法来算一个数。
我们保留小数点后5位(精度为5),0.34510=0.010112,我们用2.1.1验证,没有问题,误差在允许范围内。
2.2 八进制、十六进制与十进制之间的转换
2.2.1 八进制、十六进制转换成十进制
用2.1.1的方法,进行类比。八进制,逢8进1,进到十位上的1,实际上就是8,也就是81,百位上的1,就是82,依次类推,小数后面第1位的1,就是8-1,比如1018=1×82+0×81+1×80=6510。
同理十六进制转换成十进制也是如此,比如: 101A16= 1×163+0×162+1×161+10×160=410610,16进制的A,查表1,就是10进制里的10。
2.2.2 十进制转换成八进制、十六进制
用2.1.2的方法,进行类比,整数部分除8,除16取余数;小数部分乘8,乘16取整数。
2.3 二进制与八进制十六进制的转换
根据2.1、2.2,我们已经可以在二、八、十、十六进制之间进行转换。下面还有一种二进制与八进制、十六进制之间的简便转换方法。根据表1,找到二进制与八进制,二进制与十六进制的数值对应关系。按照下面的规则进行转换。
采用分组规则。整数部分:以小数点为中心从右向左进行分组。小数部分:以小数点为中心从左向右进行分组。
二进制→八进制:将二进制数按分组规则分成三位一组,不足补0。
二进制→十六进制:将二进制数按分组规则分成四位一组,不足补0。
比如:1101101110.1101012=36E.D41616
1101101110.11010012=1556.6448
八进制→二进制:将每一个八进制数写成对应的三位二进制数。
十六进制→二进制:将每一个十六进制数写成对应的四位二进制数。
3 总结
对照表1运算,可以很好地帮助学生对进制概念的理解;二进制转十进制,通过表1各栏的对比,学生能很容易理解和写出二进制的展开式并转成十进制;十进制转二进制,实际上是将一个由0-9组成的数字转成一个由0-1两个符号组成的数字,整数部分用除2取余数(余数只能是0或1),小数部分用乘2取整数(整数部分只能是0或1);八、十六进制与十进制互相转换也类比二进制与十进制的互相转换方法。
上述方法避免了大量的公式和算法推导,用直观、类比的方法,介绍了进制的概念和进制的转换方法,经过一学期的课堂教学发现,学生容易理解和接受,下一步打算将该知识点制作成微课。还需进一步探讨的问题有:二进制和八进制的转换为什么是三位一组;二进制和十六进制的转换为什么是四位一组;虽然查表1能很直观的看出三位二进制的最大数111正好对应一位八进制最大数7,4位二进制的最大数1111正好对应1位十六进制最大数F,这些是有待解决和探讨的问题。
参考文献(References):
[1] 赵盈颖,金耘,张帅等.计算机应用基础(第2版)[M].人民邮电
出版社,2014.