单相逆变器的滑模自适应控制器设计

王修岩，杨森

（中国民航大学航空自动化学院，天津 300300）

单相逆变器的滑模自适应控制器设计

王修岩，杨森

（中国民航大学航空自动化学院，天津 300300）

针对负载频繁变化造成逆变器波形输出严重失真的问题，基于滑模自适应控制策略，设计了单相逆变器的滑模自适应控制器。首先，建立带负载参数的逆变器数学模型，利用逆变器输出与参考信号的偏差量设计滑模面；然后将负载看作时变的参数，这样负载就成为系统的不确定部分。通过设计滑模自适应控制律，逼近不确定部分的上界，对不确定部分实现完全补偿。仿真结果表明，滑模自适应控制器在负载变化时，能够很好地跟踪系统的正弦输入，使系统有很强的鲁棒性。最后设计了实验样机，证明了控制策略的可实现性。

逆变器；负载变化；滑模自适应；鲁棒性

1 引言

逆变器是电力电子变换装置中的重要组成部分，在生产生活中有着广泛的应用：例如交流电机驱动器、不间断电源（UPS）及车载适配器等。随着它的广泛应用，对其性能的要求也越来越高，例如稳态精度高、暂态响应快等［1］。但是电源负载频繁变化时，系统的输出波形会发生严重的失真，造成输出电压不稳定。同时逆变器受到开关量控制，工作在不断变化的2个拓扑结构之间，常规的控制方法不能满足其带负载能力的要求，稳态性能较低。这种变结构特性使得滑模控制在逆变器控制中有着广泛的应用［2-4］。基于变结构理论的滑模控制最大的优点就是鲁棒性强，对参数变化和负载扰动不敏感。

但是其设计过程中需要知道扰动的界限，影响了系统鲁棒性的进一步发挥［5］。将自适应控制和滑模控制相结合，在线估计系统不确定部分的上界，然后设计滑模控制器，对进一步提高系统鲁棒性，具有很好的效果［6］。

本文在以前的基础上，首先建立全桥逆变电路的变结构模型，将负载变化作为系统参数不确定部分，然后选择滑模切换函数，设计了滑模自适应控制器，并通过Lyapunov函数证明控制作用能够保证系统的全局稳定性。仿真表明，滑模自适应控制器对负载变化具有良好的动态特性和鲁棒性。最后设计了实验样机，进一步验证了其工程的可实现性。

2 逆变器工作原理

本次设计采用单相全桥逆变电路，其原理如图1所示。VD1~VD4是全桥逆变的4个开关管，其中VD1和VD4作为一组，VD2和VD3作为一组，两组交替导通。输出采用LC低通滤波，r为考虑电感L、管压降、死区效应等［7］的等效电阻。

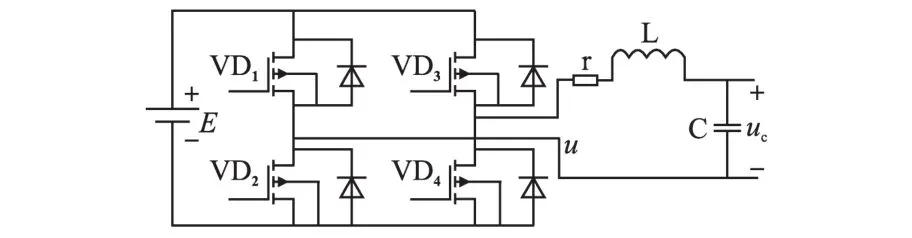
图1 单相全桥逆变电路原理图Fig.1 Circuit principle diagram of single-phase full-bridge inverter

因为逆变桥在工作过程中起到反相和比例的作用，所以在原理分析时只考虑低通滤波器的作用，其等效的电路图如图2所示，R为输出等效负载。

图2 全桥逆变电路等效电路图Fig.2 Equivalent circuit of full bridge inverter

由图2可以得到系统的传递函数

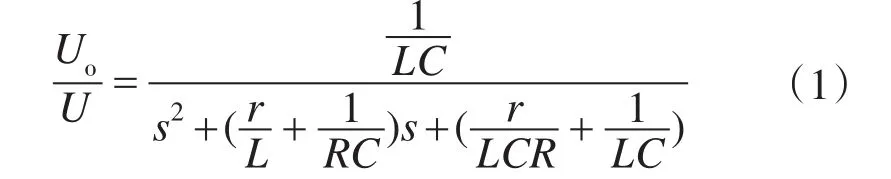
由所建立的数学模型可以看出，由于负载R可以看作系统当中的一个时变的参数，所以当负载发生变化时，被控对象的模型便发生了变化，根据不变参数设计的控制器，达不到理想的控制效果，因此需要根据当前R的参数进行控制器的设计。

3 滑模变结构自适应控制器设计

3.1 系统模型建立

由于滤波电容的电压值和电流值可以通过霍耳传感器测量，本文首先选取电容的电压uc及其导数u˙c作为状态变量，则系统状态方程可以写为

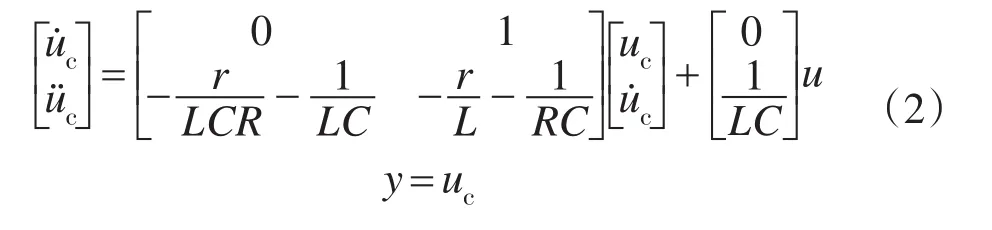
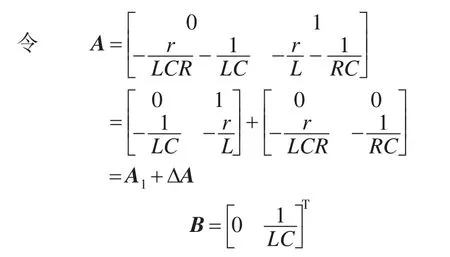
参考信号是已知的，可以采用参考信号Vref与输出uc的偏差作为新的状态变量，则系统方程可以写为

因为R是变化的，所以才导致ΔA和ΔF1(t)的存在，将ΔF1(t)看作不确定性的外部干扰。

3.2 控制器设计

滑模变结构的最大优点是滑动模态与系统的参数摄动无关，这种不变性对于一般的系统需要满足一些匹配条件，为了实现对含有不确定部分系统的控制，做如下假设。

假 设 1：rank[B，ΔA]=rankB ，即 存 在ΔA=Ba(t)，所以滑动模态与ΔA不确定性无关，可以通过设计控制律完全补偿不确定部分，rank[B，ΔA]=rankB称为不确定性与系统的完全匹配条件；同理，rank[B，ΔF1(t)]=rankB ，存在ΔF1(t)=B·f(t)，可以通过设计控制律完全补偿不确定性干扰［8］。由匹配条件可得：

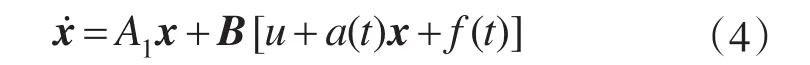
假设 1中ΔA=Ba(t)和ΔF1(t)=B·f(t)确保了不确定动态系统是稳定的，但是其上界在系统的运行过程中是很难估计的，尤其是当存在外部干扰的情况下。本文的目标就是引入一种新的自适应律，来估计不确定部分的上界，以此来设计滑模控制器，为了实现这种方法，本文做如下假设。

假设2：存在正的常数k1满足下面的不等式‖‖a(t)‖‖x+‖‖f(t)≤k1‖‖x，k1‖‖x是要通过自适应方法估计的不确定部分和干扰之和的上界。其估计值为：kˉ1(x，t)‖‖x。kˉ1(x，t)是k1的估计参数。

由式（3）取滑模切换函数：

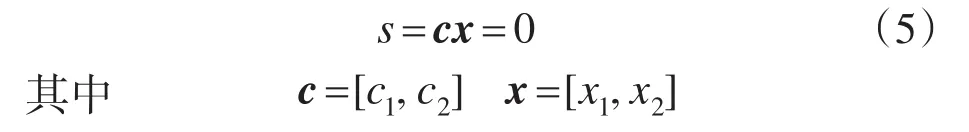
令c1＞0和c2＞0，则切换函数在相平面是一条通过原点的直线，并能保证系统的状态沿着切换函数滑动，最终稳定到原点。由式（5）可知在切换函数的滑模区域为动态一阶过程，求解为

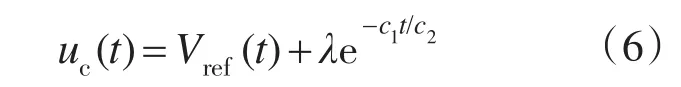
由式（6）可知切换函数的系数比c1/c2和初始状态λ共同决定了输出电压的动态过程，与其他参数无关，这体现了滑模控制对外部扰动和内部参数变化的鲁棒性。c1/c2决定了系统滑动模态的衰减速率。c1/c2比较大时可以保证系统具有快速的过渡过程和良好的动态。但是c1/c2过大又会导致滑模区域太小，甚至为零，所以选择系数比时要综合考虑滑模区域大小与跟踪的速度［9］。

理论上，滑模控制的变换器开关频率可以无限高，但在实际中是无法实现的。所以需要添加滞环延迟Δ来改善理想滑模面［10-12］，此时的滞环调制类似于离散变结构中的准滑模控制。Δ（Δ＞0）的增大，可以降低开关的频率，使开关管工作在正常的频率下，同时也有利于消除高频切换带来的抖振问题。

设计如下的控制律：

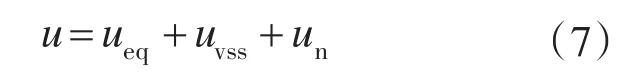
式中：ueq为标称系统的等价输入，保证系统在滑模面上滑动，最终滑动到稳定的平衡点；uvss为切换部分，保证系统向滑模趋近运动；un为匹配不确定部分的输入，实现不确定部分的完全补偿。

当s˙=0时，即cA1x+cBueq+F1=0，得到标称输入ueq=-(cB)-1[cA1x+cF1]。取切换输入2Δ为滞环调制的宽度，Δ大小影响着开关频率的确定，需要综合考虑系统各种参数的匹配问题［13］。不确定部分输入为

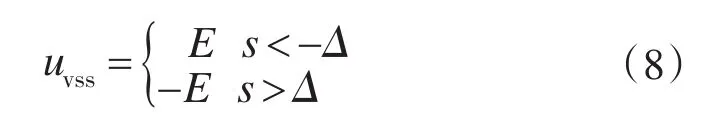
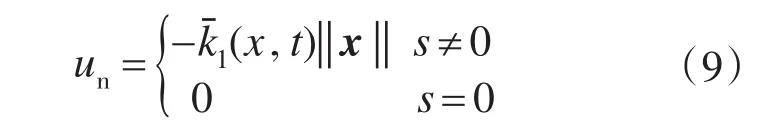
滑模自适应控制结构如图3所示。

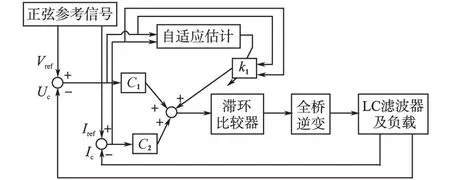
图3 滑模自适应控制框图Fig.3 Block diagram of sliding model adaptive control

对于‖‖a(t)‖‖x+‖‖f(t)的上界取以下自适应律：

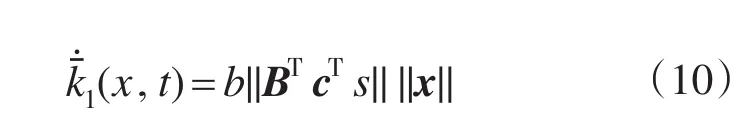
式中：b为自适应在线估计的可调增益。

通过改变b的大小，可以调整估计参数的变化率，但并不是变化率越快越好，应综合考虑系统的参数条件［14］。

3.3 稳定性分析

为了保证闭环系统全部信号的一致稳定性，取Lyapunov函数

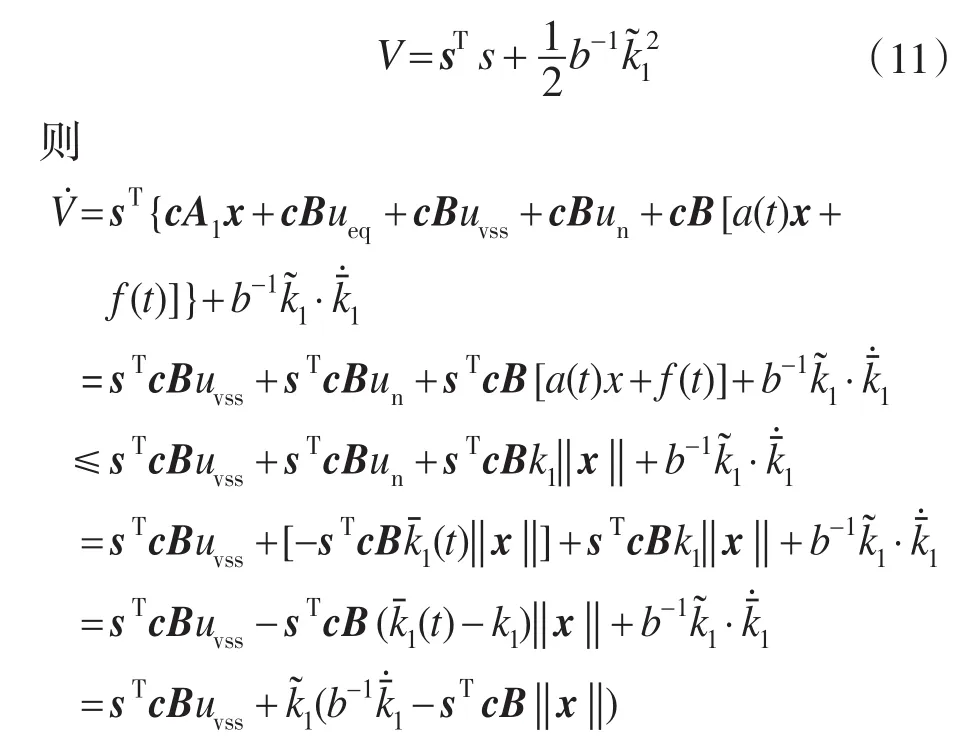
采用式（10）自适应律可以得到˙=sTcBuvss，当uvss=E，s＜-Δ，则˙=sTcBE＜0；当uvss=-E，s＞Δ，=sTcBE＜0。所以此控制器可以保证逆变器系统的全局稳定性，克服负载变化对输出波形的影响。

3.4 滑模自适应控制器的实现

输出电压、电流的采集通过霍耳传感器LV28-P、LA25-NP来实现，正弦信号由函数发生器ICL8038产生［11］。采用TLP250实现光耦隔离，集成驱动器IR2111分别驱动4只功率开关管，开关管采用IRF840，控制器硬件结构实现如图4所示。

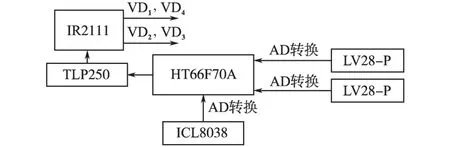
图4 控制器实现结构图Fig.4 Structure diagram of controller

采用HT66F70A单片机作为控制器的核心，其内部集成了多路AD转换模块，指令周期能达到0.25 μs，功耗低，具有PWM输出模块，其主程序流程图如图5所示。

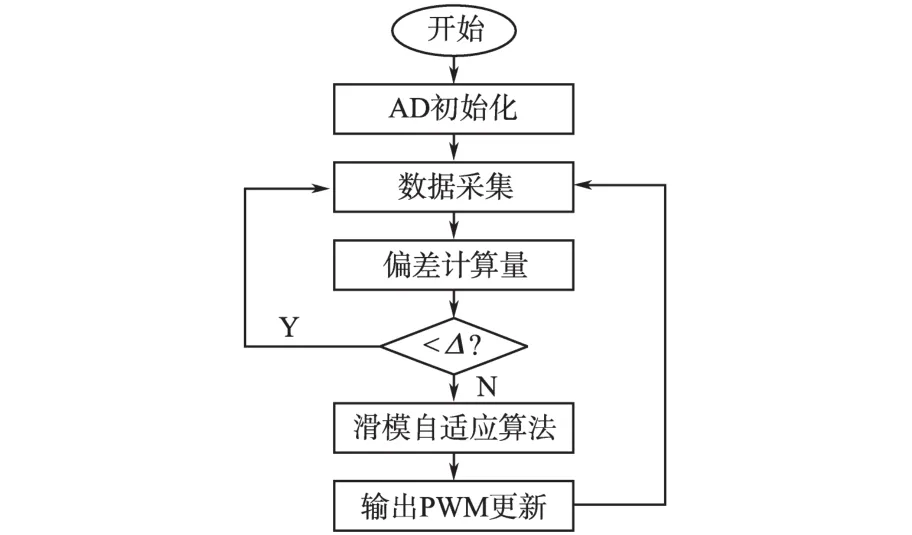
图5 主程序流程图Fig.5 Flow chart of main program

4 仿真与实验结果分析

基于以上的理论分析，首先利用Matlab进行仿真，然后设计了实验样机，逆变器仿真原理图如图6所示。实验参数如下。

1）输入电压和参考电压：E=60 V，Vref=24sin(100π)V。

2）滤波器参数：L=500 μH，C=20 μF。

3）其 他 参 数 ：c1=12，c2=0.005，b=10，r=0.05，Δ=5。

4）开关频率选择f=12 kHz。

在图6中，Controller是控制器，Us和Is分别是电压和电流传感器。通过变阻器R的变化测试控制器的有效性。将测量到的电压和电流的大小，与参考值进行比较得出偏差量，利用偏差量进行滑模自适应控制器的设计。控制器输出通过滞环比较器输出脉冲波，利用反相器，形成两路控制波形，控制开关管的通断。

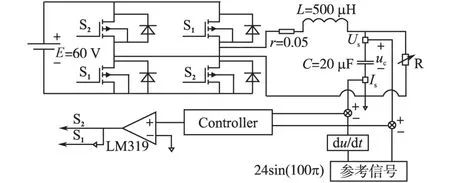
图6 逆变器仿真原理图Fig.6 Simulation schematic of inverter

将图6中的控制器改为根据固定参数设计的控制器，其仿真输出的电压和负载电流值如图7所示，Uc为输出电压，Ic为输出电流。在t=45 ms时，突然给系统加载，可以看到系统的电压值突然下降到7 V左右，很不稳定。最后电压的输出值只有20 V左右，说明根据不变参数设计的控制器在负载频繁变化时，鲁棒性差，自适应能力不强。

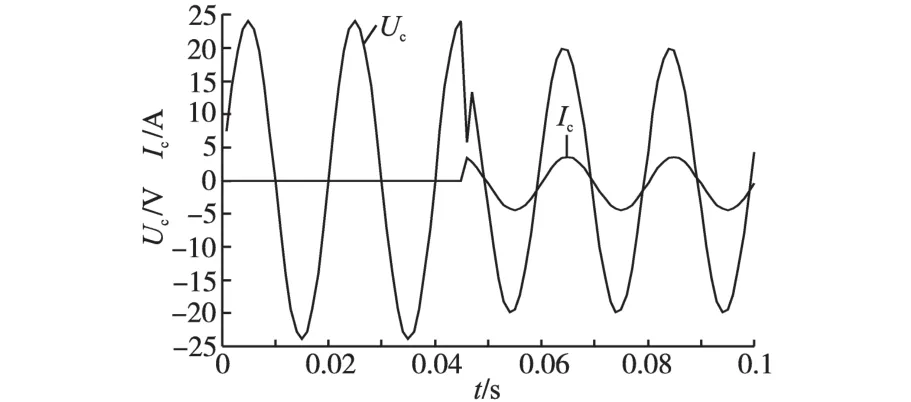
图7 不变参数控制器控制下的仿真电压电流输出Fig.7 Simulation voltage and current output controlled by unchangeable parameters controller

将图6中的控制器改为滑模自适应控制器，为了验证滑模自适应控制器对负载变化以及外部干扰具有鲁棒性的优点，当t=0时，R=0；t=45 ms时，突然加载，R=6 Ω；t=145 ms时，R从6 Ω增加到12 Ω。滑模自适应控制逆变器仿真图如图8所示。从图8中可以看出，当负载发生变化时，电压波形稳定，没有畸变，波形质量好。

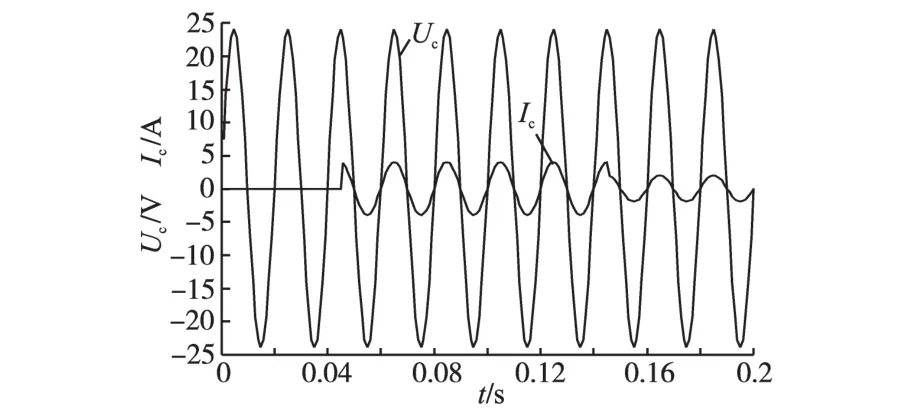
图8 滑模自适应控制逆变器仿真图Fig.8 Simulation diagram of sliding model adaptive control inverter

图9是实验样机在实验过程中电压和负载电流输出效果图。从图9中可以看出，当突然给电源加载，电流有突变，电压仍然保持稳定，没有发生畸变。仿真和实验结果一致，说明滑模自适应控制器能够提高逆变器的鲁棒性和动态性能。经过测量，输出电压总的谐波失真为0.5%，整机的效率达到90%左右。

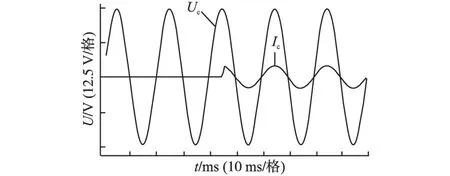
图9 滑模自适应控制实验效果图Fig.9 Experimental diagram of sliding model adaptive control

5 结论

本文将负载变化当作系统参数的不确定部分，为了消除不确定部分对输出波形质量的影响，采用自适应的方法对变化的上界进行估计，最后设计了滑模自适应控制器。仿真和实验结果表明，滑模自适应控制器具有良好的跟踪性能，在负载突变的情况下能保持良好的波形输出，使逆变器具有较强的鲁棒性。

［1］ 郭伟玮，卢晓东，冯仁剑.一种快速重复控制策略在单相逆变电源中的应用［J］.电气传动，2013，43（9）：56-59.

［2］ 桑智强，李敏远.基于滑模控制的逆变电源系统研究［J］.西安理工大学学报，2013，29（1）：98-102.

［3］ 郑雪生，李春文，汤洪海，等.三相PWM电压型逆变器的积分滑模控制［J］.电工技术学报，2007，22（12）：105-109.

［4］ 李军红，洪镇南.三相光伏并网系统的滑模变结构控制［J］.电力系统保护与控制，2012，40（12）：83-87.

［5］ 张昌凡，王耀南.滑模变结构的智能控制及其应用［J］.中国电机工程学报，2001，21（3）：27-29.

［6］ 王勃群，蔺小林.自适应滑模变结构控制算法的研究与仿真［J］.电子工程与设计，2009，30（13）：3219-3221.

［7］ 孙朝晖，吴浩伟，方斌，等.采用PID和重复控制的逆变器波形控制策略［J］.船电技术，2010，30（2）：14-17.

［8］ 刘金琨.滑模变结构控制与Matlab仿真［M］.北京：清华大学出版社，2005.

［9］ 张黎，丘水生.滑模控制逆变器的分析与实验研究［J］.中国电机工程学报，2006，26（3）：59-63.

［10］马皓，张涛，韩思亮.新型逆变器的滑模控制方案研究［J］.电工技术学报，2005，20（7）：50-56.

［11］王建华，张芳华，龚春英，等.滞环电流控制逆变器建模与分析［J］.电工技术学报，2010，25（6）：63-69.

［12］张涛.电力电子变换器中滑模变结构控制技术研究［D］.杭州：浙江大学，2006.

［13］ Ramos R，Biel D，Fossas E.A Fixed-frequency Quasi-sliding Control Algorithm：Application to Power Inverters Design by Means of FPGA Implementation［J］.IEEE Trans.on Power Electronics，2003，18（1）：344-355.

［14］吴忠强.非线性系统的鲁棒控制及应用［M］.北京：机械工业出版社，2005.

修改稿日期：2015-01-10

Sliding Model Adaptive Controller Design of Single-phase Inverter

WANG Xiu-yan，YANG Sen
（Aeronautical Automation College，Civil Aviation University of China，Tianjin300300，China）

The sliding model adaptive controller was designed to solve the problems which the load changing frequently caused output waveform distortion.Firstly，mathematical model of inverter was built with load parameter.The sliding model surface was designed based on errors between inverter outputs and reference singal.Then the load was seen as time-varying parameters，so the parameter of load would be the uncertainties of system.In order to compensate the uncertainties completely caused by load changing frequently and estimate boundary accurately，sliding model adaptive control law was designed.The simulation experiments show that，when load changing，the controller will track sine input of system accurately，which improves the robustness of inverter system significantly.Finally，an experimental prototype is designed to show realization of the sliding model control method.

inverter；load changing；sliding model adaptive；robustness

TM464

A

王修岩（1965-），男，博士，教授，Email：wangxiuyanjl@163.com

2014-08-05