单相三电平有源电力滤波器控制策略研究

谢丰，何怡刚，张金安，王东楼

（合肥工业大学电气与自动化工程学院，安徽合肥 230009）

单相三电平有源电力滤波器控制策略研究

谢丰，何怡刚，张金安，王东楼

（合肥工业大学电气与自动化工程学院，安徽合肥 230009）

将滑模控制策略运用于单相三电平有源电力滤波器中，取得了良好的控制效果。为了使电源电流为正弦波，首先建立单相有源电力滤波器的统一数学模型并分析其控制矢量图。然后计算等效控制量，根据等效控制量推导对应的矢量选择规则。此外，为了使直流侧电容电压保持均衡，通过对小矢量的选取把中点电流的积分值限制在极小的范围之内，从而使上下电容电压保持相等。最后，在Matlab/Simulink环境下对控制策略进行了仿真研究，仿真结果表明所提出的方法很好地抑制了谐波。

三电平；有源电力滤波器；滑模控制

1 引言

近年来，大量的非线性负载投入到电网中去，从而使得电力系统电压、电流波形发生畸变。有源电力滤波器（APF）作为一项动态抑制谐波和无功的措施得到了广泛的研究和应用。它既可以抑制谐波，又可以补偿无功，与无源滤波器相比，其补偿的实时性和准确性更好。

目前国内外对有源电力滤波器的研究主要集中在三相，且大多数是两电平，而对单相三电平APF的研究则不够深入和广泛。随着越来越多的单相电力电子设备的使用，单相设备对电网的危害越来越严重，而三电平有源电力滤波器在高电压、大功率方面得到了越来越广泛的重视，是目前的研究热点。因此，有必要研究一种良好的单相三电平APF控制策略来抑制电网谐波。

单相三电平有源电力滤波器的关键问题有中点电位平衡和谐波电流跟踪两个方面。在中点电位平衡问题上，本文首先分析了各个电压矢量对中点电流的影响，其次通过矢量的合适选取把中点电流的积分值限制在极小的范围之内，从而使上下两个电容的电压保持相等。

谐波电流跟踪部分，采用一种基于滑模变结构的控制策略［1］。滑模控制又称变结构控制，最早由前苏联学者在20世纪50年代提出来。滑模变结构控制的最大优点在于它的鲁棒性和快速的动态响应。国内外学者自20世纪80年代以来就进行了大量研究，已发表了大量的学术论文［2-6］。其中大多数都是将滑模控制技术应用在三相有源电力滤波器中，并取得了良好的控制效果，而其在单相有源电力滤波器中的应用相对较少。本文在前人研究的基础之上，将单相有源电力滤波器与滑模变结构控制技术相结合，提出了一种新型控制方案。

2 单相三电平有源电力滤波器拓扑结构及矢量分布图

本文采用二极管钳位型三电平变换器，其拓扑结构如图1所示。其中，非线性负载采用晶闸管相控整流电路，电力电子器件选择MOSFET，Ra，La为交流侧电阻和电感，L为平波电感，is，il，ic分别为电源电流、负载电流和有源电力滤波器补偿电流，Udc1与Udc2为直流侧电容电压。

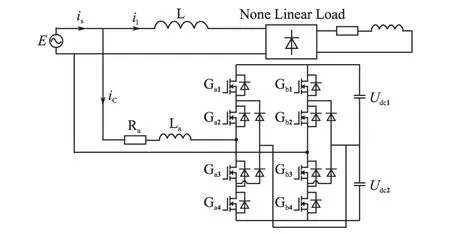
图1 单相三电平有源电力滤波器拓扑结构Fig.1 Topotype structure of single phase three-level active power filter

设左桥臂4个开关管的状态为Sa，右桥臂4个开关管的状态为Sb，并做如下规定：

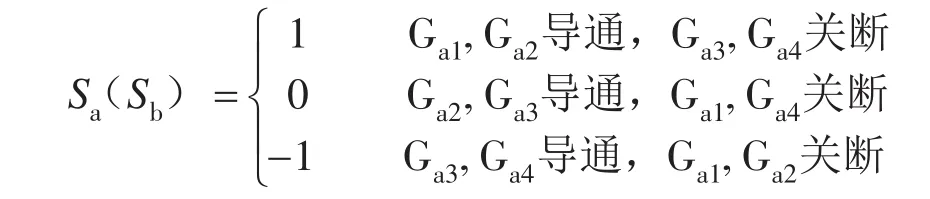
则由图1可分析出单相有源电力滤波器的数学模型为

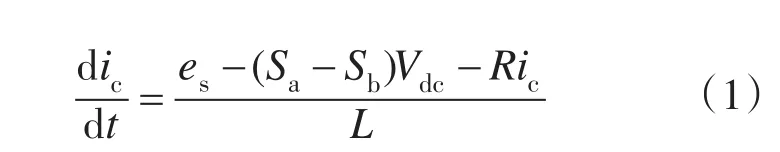
式中：es为电源电压；R为交流侧电阻。

令控制量μ=Sa-Sb，根据2个桥臂的不同开关状态，可以得到其控制矢量表，如表1所示。

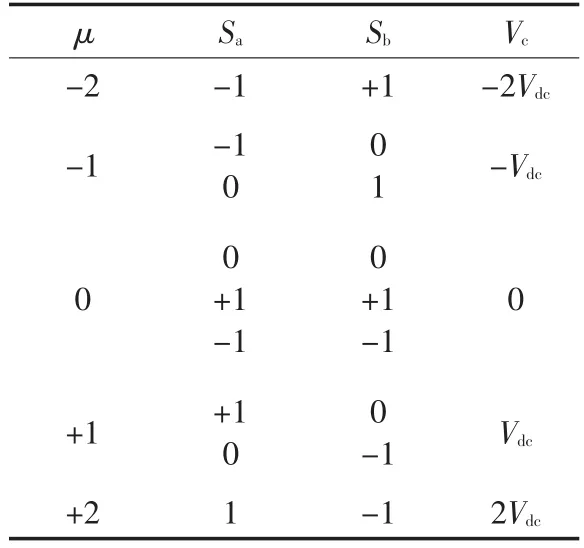
表1 控制矢量表Tab.1 Control vectors

表1中，Vdc为APF直流侧电容电压。将矢量表绘制成空间矢量图，如图2所示。

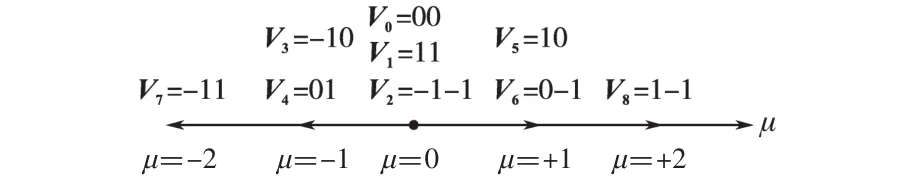
图2 单相三电平APF空间矢量图Fig.2 Space vector of single phase three-level APF

由表1及图2可以看出，单相三电平有源电力滤波器共有9种开关状态，对应5种控制量。其空间矢量图为一维平面图形，其中控制量μ=0（包含SaSb=00，11和-1-1 3种状态）位于坐标原点，对应输出电压为0；μ=1和μ=2位于正半轴，对应输出电压为+Vdc和2Vdc；μ=-1和μ=-2位于负半轴，对应输出电压为-Vdc和-2Vdc。

3 单相三电平有源电力滤波器滑模变结构控制

滑模控制的基本要求可以概括为存在性和可达性，存在性是指选取滑模函数使控制系统在滑模面上渐进稳定；可达性是指确定控制作用使所有运动轨迹在有限的时间内达到滑模面。

一般选取滑模函数s（x）=Cx，其中C为m·n矩阵。由滑模控制理论知，当满足：

则系统渐近稳定，式（2）又称为滑模控制的可达性条件，其中S为滑模面。

单相有源电力滤波器的控制目标是输出电流等于谐波电流的指令信号，因此定义滑模函数：

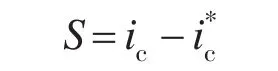
首先求取等效控制μeq，令

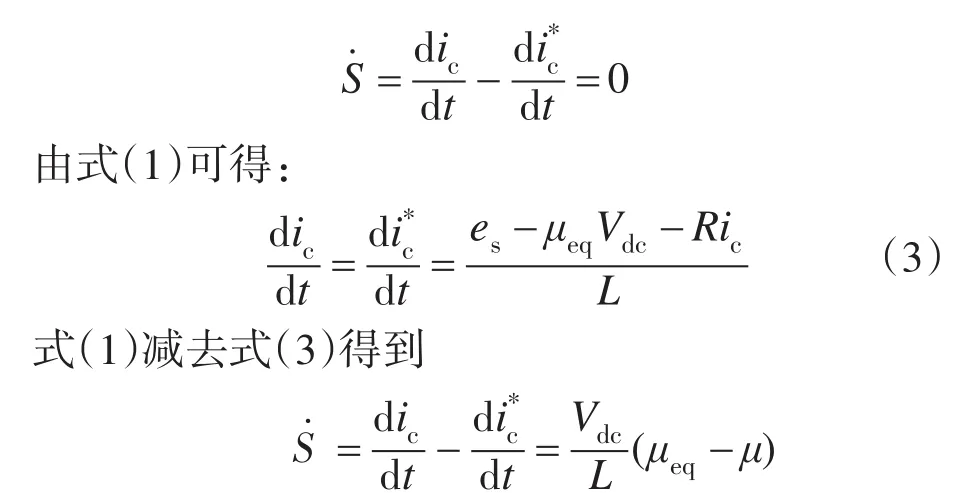
根据式（4），对应图1的空间矢量图，可以确定控制量的选择规则，如表2所示。

表2 控制量的选择Tab.2 Selection of control vector

为了使系统在可控的范围内，必须满足-2<μeq<2，否则有可能出现在某一时间段内，无论选择哪一个控制量，都无法满足可达性条件。而对μeq的控制可以通过调节Vdc的大小来实现，只要Vdc足够大，就可以把μeq限制在（-2，2）的范围内。根据仿真数据，本文选取Vdc1=Vdc2=300 V，可以满足要求。

对表2研究发现，在某些区间里可能出现多个控制量同时满足可达性条件，那么有必要分析确定具体应当选择哪一种控制量。

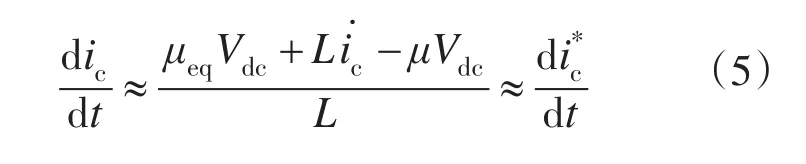
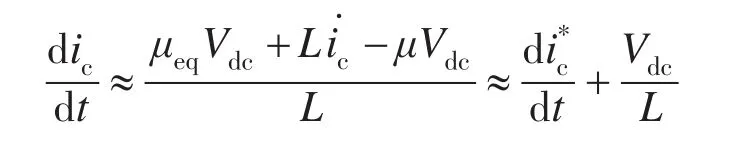
由上式可以看出，实际输出电流变化率远远大于指定电流变化率，满足了快速性要求。若选择μ=-2则实际输出电流变化率将更大，但此时容易产生较大的电流纹波，出现毛刺现象。因此综合考虑，选择μ=-1比较合适。以此类推，当μeq的值与某一个特定的μ值十分接近时，则不宜选取这个μ值作为输出量；同时，当μeq的值不与某一特定μ值非常接近时，则可以选择该控制量作为输出，这样能够减少电流纹波。那么μeq与某一特定的μ值的接近程度应当有一个量化的标准，这需要通过实验反复选取得到。本文选择当μeq与μ相差0.2作为临界情况。通过以上分析，得出控制量的优化选择，如表3所示。

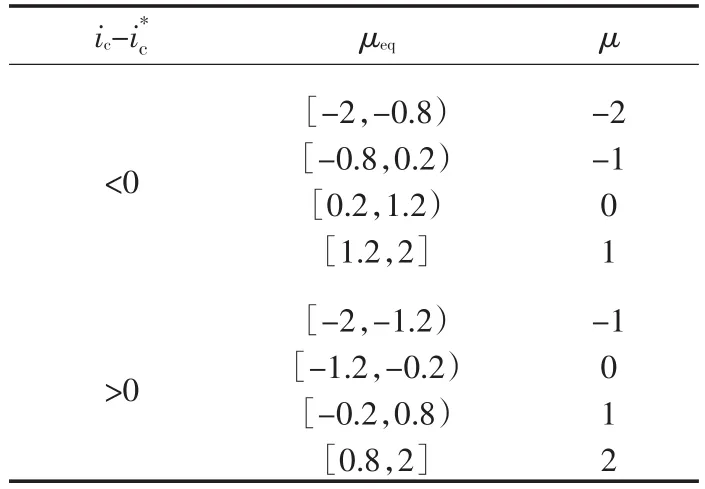
表3 控制量优化选择Tab.3 The optimization selection of control vectors

4 直流侧电压控制

4.1 总体电压控制［7-8］

本文采用基于单相电路瞬时无功功率理论的谐波检测方法，其基本框图如图3所示。

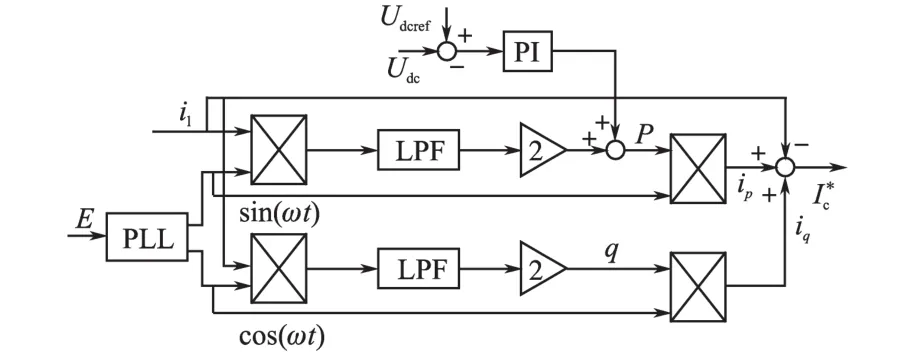
图3 单相电流谐波检测Fig.3 Harmonic detection of single phase current

图3中，E=Usin(ωt)为电网电压，PLL为锁相环，LPF为低通滤波器，p，q为单相电路的基波瞬时有功电流和无功电流的幅值，分别与sin(ωt)与cos(ωt)相乘后即为基波瞬时有功电流和无功电流。如果既要滤除谐波又要补偿无功，则只需将q通道断开即可。

为了使直流侧电压保持恒定，将Udc的给定值与测量值相减，再经过PI调节，得到调节信号Δp，把它叠加到瞬时有功电流上去，这样指令电流中包含一定的基波有功分量，从而使得有源电力滤波器的直流侧与交流侧交换能量，将直流侧电容电压调节到给定值。

4.2 电容均压控制

与两电平有源电力滤波器不同的是，三电平有源电力滤波器不仅要维持2个电容电压之和保持不变，还要维持2个电容电压相等，这就是电容均压问题。首先给出单相三电平有源电力滤波器的简化拓扑结构，如图4所示。

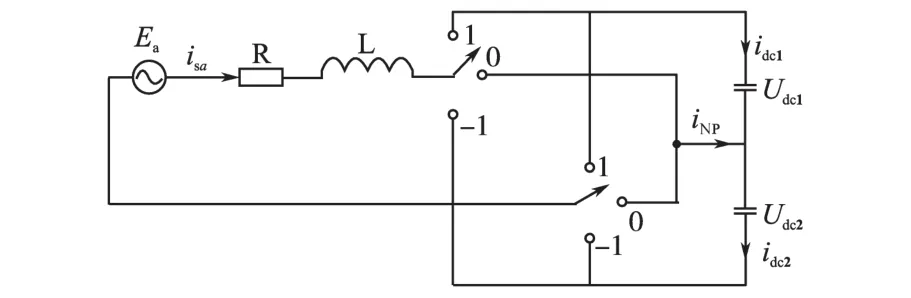
图4 单相三电平有源电力滤波器简化模型Fig.4 Simplified model of single phase three-level active power filter

由图4可以分析出选择不同开关状态时的中点电流iNP的值，如表4所示。

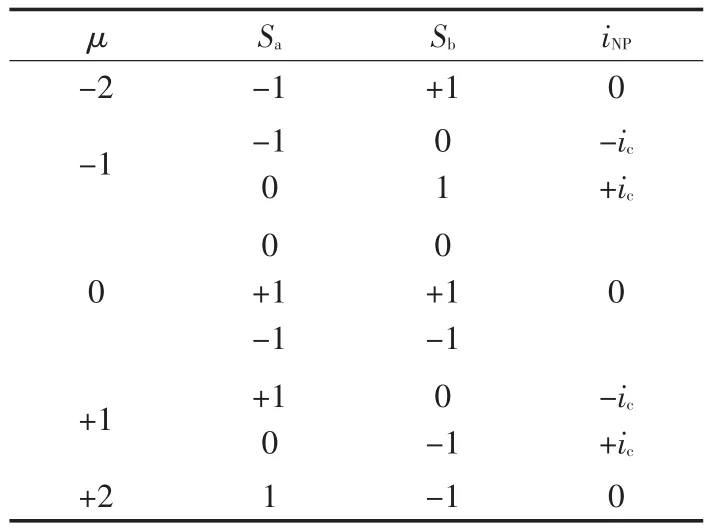
表4 各矢量对中点电流的影响Tab.4 The effects of the vectors on neutral current

由表4可以分析出只有μ=+1或者-1对中点电流有影响，而其他状态对中点电流没有影响。且同一个控制量对应的2种开关状态对中点电流的影响是相反的。

下面分析如何使得Udc1=Udc2。由电路理论知识可得：

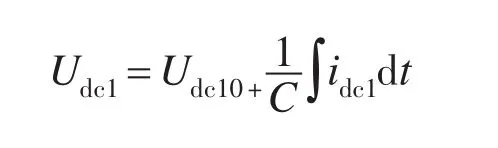
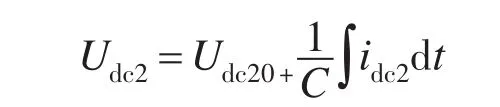
式中：Udc10+，Udc20+为2个电容电压的初始值。当我们设定Udc10+=Udc20+=0时，则有

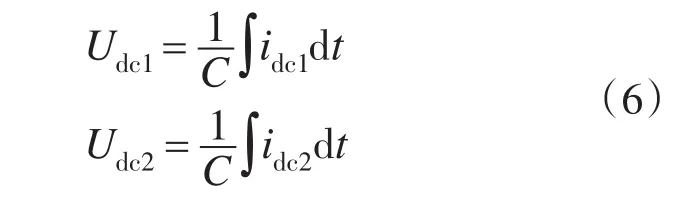
式中：C为直流侧电容值。

由图4得

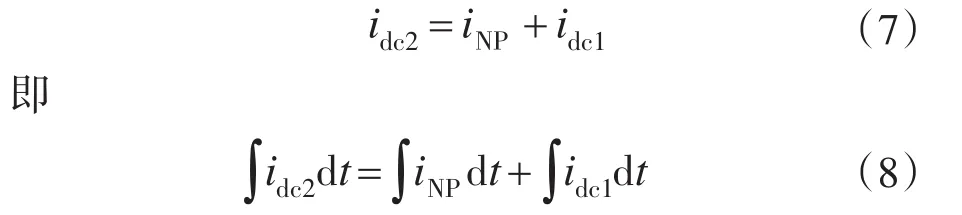
综合式（6）~式（8）可知，要想使Udc1=Udc2，则必须满足：

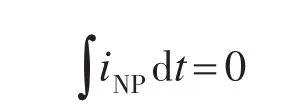
若要使上式恒为0，则中点电流应恒为0，这是不可能的，因此我们只能把中点电流的积分值缩小到一个很小的范围内，这样就可以维持2个电容电压保持基本相等。因此，必须对中点电流进行检测，并对其进行积分，以此来判定应当选择哪个矢量。例如，当由表3得出此时应当选择矢量-10或01时，若iNP的积分值大于0且ic>0，或者iNP的积分值小于0且ic<0，则应选择矢量-10，之后iNP的积分值向0靠近；反之若iNP的积分值小于0且ic>0，或者iNP的积分值大于0且ic<0，则应选择01，之后iNP的积分值向0靠近。具体选择规则如表5所示。

表5 考虑中点电压后的矢量选择Tab.5 Selection of vector after considering the neutral voltage

实际操作中若无法检测中点电流则可以检测Udc1-Udc2的值当做中点电流的积分值。

5 仿真结果

为了验证本文提出的控制策略，利用Matlab软件进行了仿真研究。仿真参数如下：电源电压为220 V；交流侧电感为3 mH；交流侧电阻为0.3 Ω；直流侧电容为8 000 μF；直流总给定电压为600 V；平波电感为3 mH；PI参数为Kp=0.2，Ki=0.2；单个电容电压为300 V。有源电力滤波器没有接入系统时的电流波形如图5所示，由图5可知，未接入有源电力滤波器之前电流波形严重畸变，无法满足电力系统的要求。

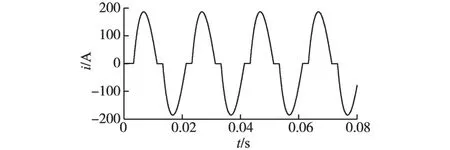
图5 负载电流波形Fig.5 Load current waveform

接入有源电力滤波器之后的各波形如图6~图11所示。其中图6给出了APF的补偿电流波形，补偿之后的电源电流波形如图7所示。从图7中可以看出，由于滑模控制策略使APF电流环取得了良好的动态特性，因而使APF很好地抑制了谐波。加入APF之后，电网电流已经几乎变成了正弦波，通过图8快速傅里叶分析可以看出，其总谐波畸变率已经降为1.39%，完全满足了国家标准中小于5%的要求。直流侧总电压如图9所示，可以看出，直流侧电压在经历很短的时间之后就稳定在了600 V左右，满足了要求；上下2个电容的电压差值如图10所示，可以看出，电容电压差值已经非常接近0，满足了控制系统的要求。μeq的值如图11所示，其值被限定在了（-2，2）的范围，满足控制要求。

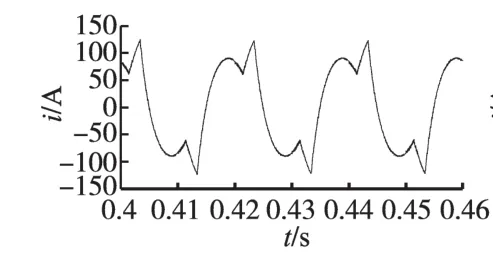
图6 有源电力滤波器补偿电流Fig.6 Compensation current of active power filter

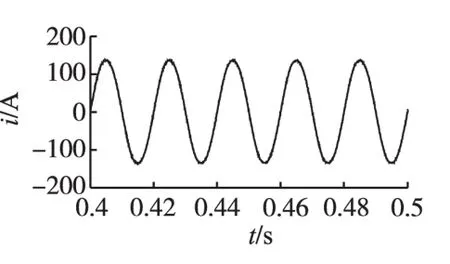
图7 补偿后电源电流Fig.7 Power current after compensation

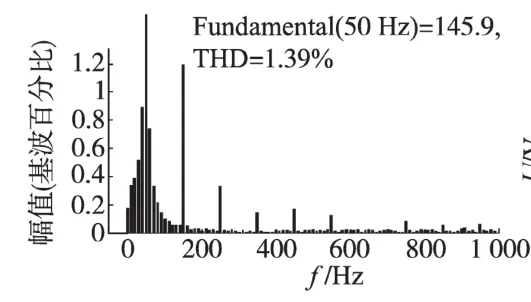
图8 电源电流傅里叶分析Fig.8 FFT analysis of source current

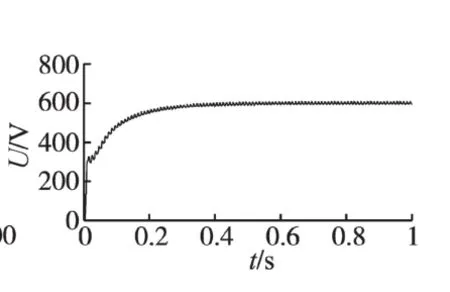
图9 直流侧电压Fig.9 DC voltage

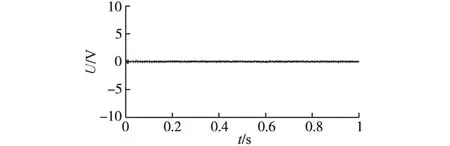
图10 电容电压差值Fig.10 Capacitance voltage difference

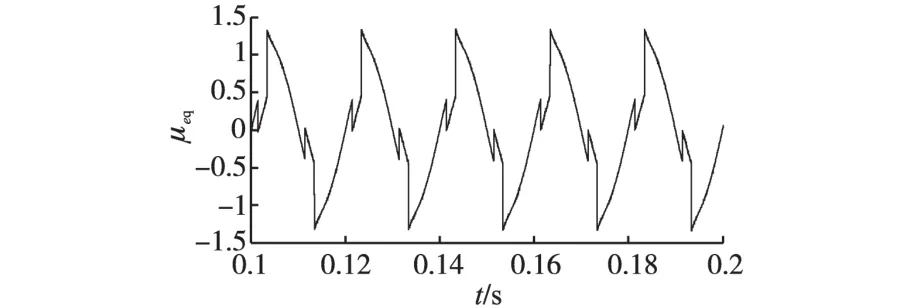
图11 μeq的值Fig.11 The value ofμeq

6 结论

本文将单相三电平空间矢量概念与滑模变结构控制技术相结合，提出了一种应用于单相三电平有源电力滤波器的新型控制策略。其中电流环部分通过等效控制的方法推导出了滑模变结构控制规则；而在电压环部分通过向检测到的有功电流中加入一定的基波有功分量来维持2个电容电压的总体值保持恒定，此外，通过对μ=±1对应的2个矢量的选取来控制中点电流的积分值保持在极小的范围之内，进而控制上下2个电容电压保持基本一致。Matlab仿真结果表明，本文提出的方法很好地抑制了谐波，且使直流侧电容电压值保持了均衡。

［1］ 张兴，张崇巍.PWM整流器及其控制［M］.北京：机械工业出版社，2012.

［2］ 鞠建永.基于滑模控制的并联型有源电力滤波器［D］.合肥：合肥工业大学，2002.

［3］ 侯志军.基于滑模控制的电力有源滤波器研究［D］.兰州：兰州理工大学，2010.

［4］ Somayeh Yarahmadi，Gholamreza Arab Markade，Jafar Soltani.Current Harmonics Reduction of Non-linear Load by Using Active Power Filter Based on Improved Sliding Mode Control［C］//PEDS TC2013，2013：524-528.

［5］ Pempeo Marino，Froncesc Vasca.Sliding Mode Control for Three Phase Rectifier［C］//IEEE PESC1995，1995：1033-1039.

［6］ Dr.Vitthal S Bandal，Priti N Madurwar.Performance Analysis of Shunt Active Power Filter Using Sliding Model Control Strategy［C］//VSS2012，2012：214-219.

［7］ 吴义敏.应用于有源电力滤波器的单相谐波检测的研究［D］.合肥：合肥工业大学，2012.

［8］ 刘佳.单相并联型有源电力滤波器研究［D］.武汉：华中科技大学，2009.

修改稿日期：2014-12-15

Research on Control Strategy for Single Phase Three-level Active Power Filter

XIE Feng ，HE Yi-gang，ZAHNG Jin-an，WANG Dong-lou
（School of Electrical Engineering and Automation，Hefei University of Technology，Hefei230009，Anhui，China）

Put forward a novel control strategy for single phase three-level active power filter（APF）by using the sliding mode control（SMC）technology and achieved good results.For the sake of optimal control goal to enable the source being sinusoidal，established the mathematical model for single phase APF，analyzed its control vectors and calculated equivalent control，then the corresponding vector selection rule was deduced based on the equivalent control.In addition ，in order to make the DC side capacitors voltage be balanced，used the small vector to restrict the integral value of neutral current to a scope of minimal，then the voltage between the two capacitors were equal.The simulation in Matlab/Sinmulink was provided to verify the proposed control strategy，the simulation results show that the proposed method is good enough to suppress the harmonic.

three-level；active power filter；sliding model control

TM464

A

国家杰出青年科学基金（50925727）；国防科技计划项目（C1120110004，9140A27020211DZ5102）；教育部科学技术研究重大项目（313018）；安徽省科技计划重点项目（1301022036）

谢丰（1989-），男，硕士研究生，Email：xiefeng31489@126.com

2014-06-12