深水悬链锚泊系统等效截断水深优化设计

樊天慧，乔东生，欧进萍

（大连理工大学a.建设工程学部；b.深海工程研究中心，辽宁大连116024）

深水悬链锚泊系统等效截断水深优化设计

樊天慧a，b，乔东生b，欧进萍a，b

（大连理工大学a.建设工程学部；b.深海工程研究中心，辽宁大连116024）

工程中，常用的深水悬链锚泊线通常是由顶部锚链、中部钢索和底部锚链三段复合而成。该文采用分段外推的数值解法，考虑锚泊线所受的重力、张力、流力以及锚泊线的弹性伸长，利用黄金分割算法求解锚泊线顶端张力对应的顶张角，对其进行静力特性分析。基于混合模型试验方法应用，考虑锚泊系统静力特性相似，采用遗传算法编制开发等效截断水深系统优化设计程序。以一座工作水深为1 500 m的深水半潜式平台为例，对其悬链式锚泊系统在700 m水深处进行等效截断优化设计计算，为下一步进行混合模型试验提供参考。

深水悬链线；分段外推；混合模型试验；截断优化设计

0 引言

虽然凭借流体力学和结构力学现有水平，利用高性能计算机和各种专业软件，可以通过数值方法得出所需的技术数据。然而，由于计算中常引入诸多理想假定或经验数据，计算结果可靠度欠佳。因此，迄今为止，海洋工程界仍然一致认为物理模型实验的结果最为可靠，并以此作为设计、建造海洋平台的最终依据。

人类的生存和发展离不开能源，陆地和浅海地区油气资源已然开发殆尽，深海地区丰富的油气资源必然会吸引业界和科研人员目光的聚焦。模型试验水池的尺度有限，随着海洋工程的发展，工作水深的增加，目前的模型试验水池尺度已经不再能满足实际工程的需要。同时，水池尺度不能因为作业水深的增加就无限制地扩展。因此，我们必须关注物理模型试验新方法的研究，使得我们能够在现阶段的模型试验水池中较好地完成深水平台物理模型试验。在这些新的方法中，混合模型试验无疑是其中最具有发展潜力的实验方法[1]。

截断水深下锚泊系统的等效设计是混合模型试验过程中比较重要的一环，其截断的方式主要有两种：主动式和被动式。目前广泛应用的是基于静力特性一致的被动式截断水深等效设计。在Stansberg等[2]提出混合模型试验方法之初，截断水深锚泊系统的设计是通过工程师们进行试算，并根据截断系统和全水深系统静力特性的差别进行调整直到其静力特性基本一致的方式来完成的，其设计精确度不理想且费时费力；其后，MARINTEK的开发团队编制了相应截断优化程序MOOROPT-TRUC程序来满足等效设计要求[2]。Zhang等[3]应用四阶龙格—库塔法求解单根锚泊线的静力特性，并应用拉格朗日插值法插值计算整个锚泊系统的静力特性，并基于模拟退火法对截断水深等效锚泊系统进行优化设计。苏一华等[4]基于悬链线方程求解锚泊系统静力特性，结合NSGA-Ⅱ算法优化设计等效锚泊系统。王宏伟等[5]根据静力特性相似准则针对不同形式的锚泊线提出三种截断准则。Udoh[6]根据弹性悬链线理论计算了锚泊系统的静力特性和回复力刚度，并应用Excel对截断系统进行等效设计。

本文以一座深海半潜式平台使用的三段复合悬链线锚泊系统为例，首先采用分段外推的数值方法，研究锚泊线受到重力、张力、流力以及考虑锚泊线弹性伸长情况下的单根锚泊线的静力特性；然后分析整个锚泊系统的静回复力特性；最后基于静力等效设计原则[1-2，7]采用遗传算法，对其锚泊系统进行等效截断优化设计，并完成程序的编制工作。

1 深水悬链锚泊系统静力特性分析

1.1 运动控制方程

本文以顶部锚链、中部钢索和底部锚链三段复合而成的深水锚泊线为研究对象，无论锚泊线处于松弛或者张紧情况，其运动控制方程按照如下形式进行求解：

在锚链线上任意取一微段，对其进行受力分析，如图1所示，可以得到其静平衡方程。在忽略二阶无穷小量后，得到[8]：

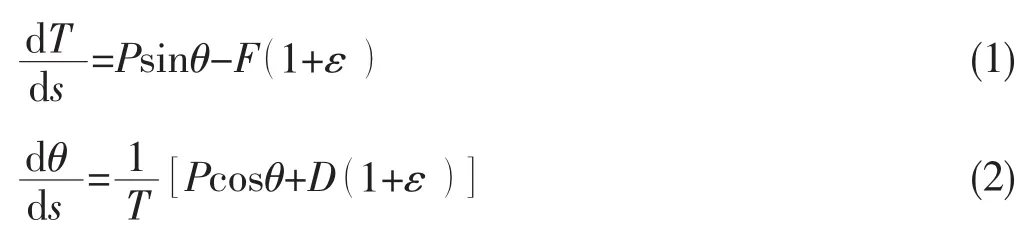
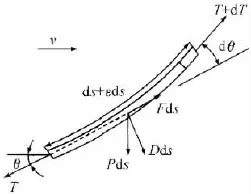
图1 锚泊线上任意微段受力分析图Fig.1 Arbitrary element of mooring line

式中：T为锚链两端拉力；dT为ds上的拉力变化量；θ为拉力T的倾角；dθ为ds上的倾角变化量；F和D分别为单位长度上的切向和法向流拖曳力；P为锚泊线单位长度水中重量；ε为锚泊线单位长度上的伸长量。其中：

式中：E为锚泊线材料弹性模量；A为锚泊线的横截面积；ρ为海水密度；Vc为海流速度；CN为法向阻力系数；CT为切向阻力系数。

从几何关系则可得到：

由（6）式和（7）式可以求得锚泊线上任意一点的坐标值。

1.2 求解方法

采用分段外推法对单根锚泊线的静力问题进行求解，首先要进行单元的划分。把锚泊线的顶部A B、中部B C和底部O C分别划分成n1、n2和n3个单元，如图2所示。这样锚泊线的总单元个数为n个。其中，n=n1+n2+n3。

各单元重量及外荷载均集中在单元的中心上，作用于单元中心的外载荷有重力和海流力。对任意单元i进行受力分析，根据公式（1）和（2）可以得到单元i上的平衡方程[9]：

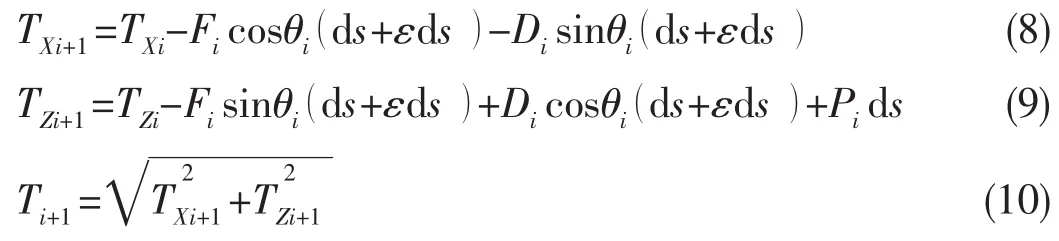
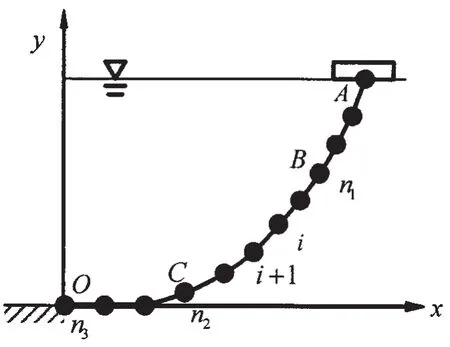
图2 锚泊线单元划分示意图Fig.2 Mooring line elements

式中：TXi和TXi+1分别为第i和i+1单元的水平力；TZi和TZi+1分别为第i和i+1单元的竖向力；Di和Fi分别为第i单元的垂向和切向的单位长度的海流力。

根据公式（6）和（7）可以得到单元节点坐标的空间关系：

在已知锚链第一个单元受力在X、Z方向的分力的情况下，求解过程用迭代方法。计算过程如下[10]：

（1）假设一个锚泊线顶端的水平方向的夹角θ；

（2）把不均匀锚链分段分别划分成若干个单元，将每个单元上的重力和水流力都简化到单元的中心上；

（3）把前一段锚链的末端点作为下一段锚链的起点；

（4）根据上式求出锚链上各段的受力T和各点的坐标值x，z；

（5）验证水深边界条件，也就是最后一点坐标是否为水深H。如果满足这个边界条件则结束计算，否则返回（1），重新计算。

通过上述过程，即可求得特定顶张力对应的锚泊线顶张角，从而得出锚泊线的各个点的力和坐标。因此，对于给定的锚泊线属性，每给出一个顶张力，即可求出顶张力对应的顶张角和锚泊线的横距。

求顶张角的过程可以考虑成一个一维寻优的过程：计算得到锚泊线的布线深度和水深之间差值的绝对值可以考虑成一个以顶张角为自变量的连续函数，并且这个函数具有单峰值。所以，本文在编程的时候选择黄金分割算法进行求解。该方法通过比较优化区间内部两个黄金分割点的值和端点值，来缩短优化区间的方法来达到寻优目的。每一次计算得到的新区间长度都是上一个计算步区间长度的0.618倍，收敛速度快，精度高。

1.3 锚泊系统的静力分析

截断锚泊系统的等效优化设计过程中，需要用到锚泊系统静回复力特性。计算过程为：

（1）根据给定的单根锚泊线属性和平台提供给锚泊线的预张力，确定顶张力区间，并计算区间内顶张力与锚泊线横距的关系，为计算锚泊系统回复力提供基础。顶张力的区间要根据给定的预张力来确定，既要包含预张力，又要取到预张力两端足够大的范围，即在平台水平移动的过程中，锚泊线的最大顶张力和最小顶张力都要包含在张力区间范围内。在张力区间内平均取点，通过计算每个张力对应的锚泊线横距，即可得到顶张力与横距的关系曲线。

（2）根据平台的水平移动，计算锚泊系统中每一根锚泊线的横距。依次给出平台水平移动（沿X轴正方向）距离dx（一般以系统初始静平衡位置为0点），用偏移的步数控制偏移的距离。对于每一步偏移位置，根据锚泊线布锚角的分布来计算各根锚链的新横距[11]。新横距的计算方法示意图如图3所示。根据余弦定理，知道初始位置的布锚角和横距，即可求出对应于平台移动到dx位置的新横距和布锚角，而之后每一偏移步的横距和布锚角均可由上一偏移步通过余弦定理求得。

（3）通过步骤（2）计算得到的每一偏移步每根锚泊的横距，利用在步骤（1）中得到顶张力与横距的关系曲线进行线性插值计算得到响应的顶张力；根据每一偏移步中每根锚泊线的顶张力和布锚角，即可计算出当前偏移量下整个锚泊系统的静回复力和单根锚泊线的回复力。

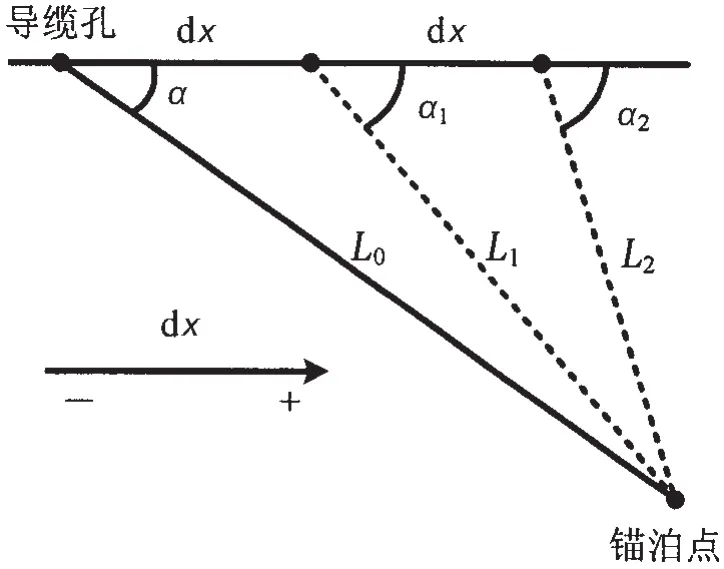
图3 平台移动俯视示意图Fig.3 Top view of the mooring line positions

2 截断锚泊系统的优化设计

2.1 截断优化设计准则

在完成等效截断系统设计的时候，现今为止依据的基本准则如下[1]：

（1）具有代表性的单根锚链回复力特性和全水深系统一致；

（2）截断系统的总体回复力特性和全水深系统一致；

（3）平台耦合运动和全水深系统准静定一致；

（4）截断系统的阻尼水平和全水深系统一致。

当然，以上设计要求并不要求同时做到。原则上，保持截断锚泊系统静回复力特性和全水深系统基本一致即可。

在等效截断锚泊系统优化设计过程中，使用浮子、重块和弹簧的措施将会使混合模型试验的后续步骤—数值重构和数值外插遇到障碍。其在等效截断锚泊系统中的应用会导致截断系统和全水深系统在动力特性上的未知差异，并且其特性难以模拟。因此，本文只对锚泊线的材料属性和长度进行模拟。

2.2 基于遗传算法的优化设计

对等效系统的截断优化设计是对锚链参数的一个大范围的寻优过程。本文考虑满足锚泊系统静力特性的一致性，确定了满足2.1小节所述的准则（1）、（2）的目标函数：

其中：i为第i位移步；N为位移步数；Fxt，i为截断系统第i位移步锚泊系统提供的水平回复力；Fzt，i为截断系统第i位移步锚泊系统提供的垂向回复力；Tt，i为截断系统第i位移步有代表性的单根锚链张力；Fxf，i为全水深系统第i位移步锚泊系统提供的水平回复力；Fzf，i为全水深系统第i位移步锚泊系统提供的垂向回复力；Tf，i为全水深系统第i位移步有代表性的单根锚链张力。

由于目标函数复杂，截断锚泊系统和全水深锚泊系统回复力特性计算量大，本文采用适应性较强的智能优化算法—遗传算法对锚泊系统的参数进行寻优设计。其过程如下[12]：

（1）编码：对需要优化的锚链参数进行二进制编码；

（2）初始化：设置进化代数计数器t=1，设置最大进化代数T，在锚链参数的变量空间中随机生成M个个体作为初始群体P（1）；

（3）个体评价：根据目标函数公式编写适值函数，计算群体P（t）中各个个体的适应度；

（4）选择运算：将选择算子作用于群体，筛选出优秀的个体，作为交叉变异的对象；

（5）交叉运算：将交叉算子作用于步骤（4）筛选出的优秀个体，把两个父代个体的部分结构加以替换重组而生成新个体；

（6）变异运算：将变异算子作用于步骤（4）筛选出的优秀个体，把个体串的某些基因位上的基因值作变动；

（7）群体P（t）经过选择、交叉、变异运算之后得到下一代群体P（t+1），返回步骤（2）进行计算；

（8）终止条件判断：设置最优解的适值函数的容许值，如果优化过程中出现小于容许值的适值函数，则终止运算；如果达到最大进化代数，则所得到的最优个体作为最优解输出，终止计算。

3 算例与结果

选用某一深海半潜式平台作为研究对象，其工作水深为1 500 m。锚泊系统由4组，每组各3根锚泊线组成。1号锚泊线到12号锚泊线的初始位置布锚角依次为40°、45°、50°、130°、135°、140°、220°、225°、230°、310°、315°和320°，如图4所示。

该半潜式平台采用悬链式锚泊方式，单根锚泊线采用顶部锚链、中部钢索和底部锚链复合而成。主要参数如表1所示，预张力为1 600 kN。

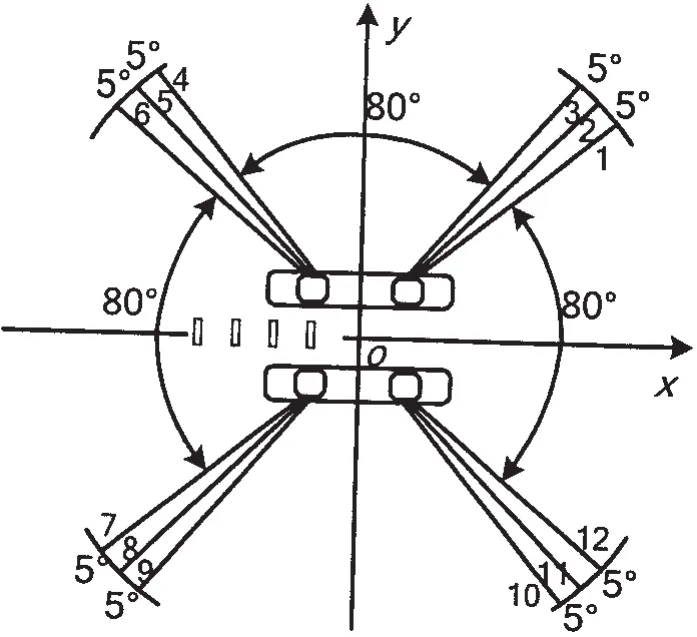
图4 锚泊系统布置示意图Fig.4 Layout of mooring lines

表1 全水深平台单根锚链参数Tab.1 Parameters of the full-depth mooring line

大连理工大学的深水实验室，最大工作水深为10 m，按照海洋工程中物理模型试验的常用缩比尺1：70来进行设计，那么截断水深设定为700 m。由于等效截断锚泊系统的设计，是为混合模型试验服务的，而浮子、重块和弹簧的使用会改变锚泊系统的水动力作用，使其很难被软件模拟，其对数值重构和数值外插过程形成阻碍。故本算例中，只对锚泊系统的材料属性和长度进行优化设计。顶部和底部的锚链直接按照水深截断比例缩短，其材料属性不改变，长度分别为140 m和700 m。对中部钢索的3个参数：长度l、浮容重P和轴向刚度EA进行优化。

约束条件为：300≤l≤1 200；100≤EA≤2 000；100≤P≤2 000。

本文采用2.2小节中提到的优化设计准则，以满足截断系统和全水深系统的水平回复力、垂向回复力和具有代表性的2号锚链张力一致为需求，设计的目标函数如下：

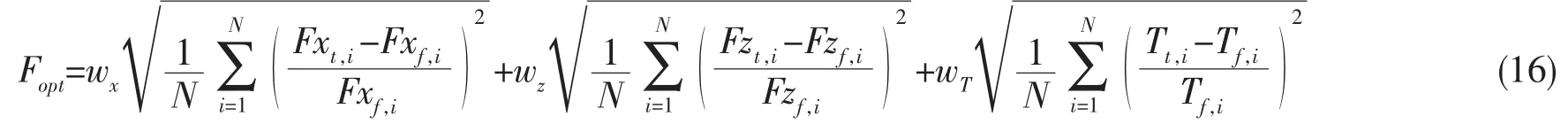
式中：wx、wz和wT分别为系统的水平回复力、垂向回复力和具有代表性的2号锚链的张力的权值函数。由于水平方向的回复力静力一致性要求最高，所以权值wx、wz和wT分别取0.4、0.3和0.3。

在遗传算法中，根据Matlab帮助文档，设定精英数量为初始种群数的10%，交叉比例为0.8，变异比例为0.2，上述参数设定计算稳定，收敛速度较快，适用性强。优化过程中，初始种群数的大小和最大进化代数也在一定程度上决定了优化结果的精确度和计算时间。在不设置差异度精度要求的情况下，经过计算，在初始种群数取值为20，最大进化代数为50代的情况下，所得到的目标函数的值也就是等效系统和全水深系统静力特性的差异度会控制在5%以内。随着初始种群数量和最大进化代数的增加，差异度将会减小。然而，随着初始种群数量和进化代数的增加，程序计算需要时间增加很快，而差异度的降低却并不明显。考虑平台水平位移达到100 m的情况下，当初始种群数为40，最大进化代数为120的时候，优化计算的平均时间将会增加到约5小时，两个系统静力特性的差异度会保持在3%左右。设定差异度精度要求为小于4%，在初始种群数取值为20，最大进化代数为100代的情况下，优化设计的完成过程平均耗时约为1.3小时，得到等效截断锚泊系统与全水深锚泊系统的静力特性的差异度在4%以内。

最终得到锚链参数的优化结果如表2所示，相应的截断系统与全水深系统静力特性对比情况如图5-7所示。

表2 截断系统锚泊线参数优化结果Tab.2 Parameters of the truncated mooring line

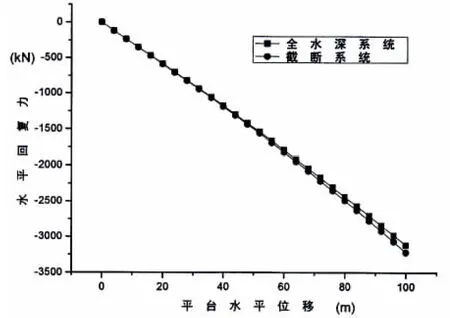
图5 截断系统与全水深系统水平回复力对比图Fig.5 The horizontal restoring force of mooring system

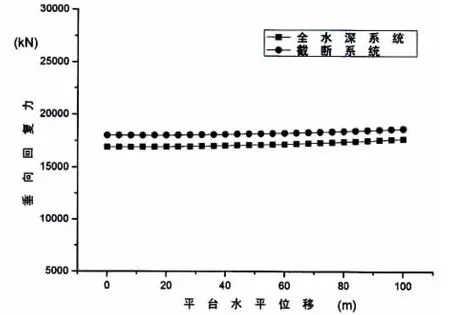
图6 截断系统与全水深系统垂向回复力对比图Fig.6 The vertical restoring force of mooring system

4 结语

采用分段外推法求解锚泊系统静力特性，基于静力特性一致的等效截断原则，应用遗传算法编制开发了等效截断水深锚泊系统的优化设计程序。以一座深水半潜式平台的悬链式锚泊定位系统为研究对象，应用上述程序对其进行分析，得到以下结论：

（1）不使用浮子、重块和弹簧等措施，只对锚泊系统的材料属性和长度进行优化设计，即可得到静力特性与全水深锚泊系统基本一致的截断水深锚泊系统；

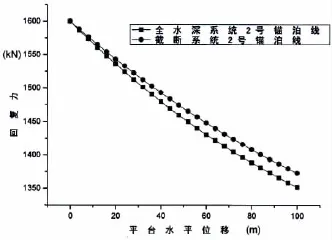
图7 2号锚链张力特性对比图Fig.7 The tension of No.2 mooring line

（2）该等效截断锚泊系统优化设计程序可以解决多变量、多目标的截断水深锚泊系统优化设计问题；

（3）在采用分段外推法求解锚泊系统静力特性的过程中，使用黄金分割法寻求顶张角，使得分析锚泊系统静力特性的子程序拥有更高效率；

（4）初始种群数取值为20，最大进化代数为100代，平均耗时1.3小时即可得到误差在4%范围内的优化结果，而选取更高的初始种群数量和进化代数对优化结果影响较小且耗时过长。

文中程序具有很强的适用性和可推广性。按照文中的参数设定，该程序可以应用于其他深水悬链锚泊系统的截断优化设计。基于静力特性一致的等效截断锚泊系统的优化设计是进行混合模型试验的基石，高效优化设计方法和优化程序的开发为混合模型试验的后续步骤奠定了坚实的基础。

[1]Stansberg C T,Ormberg H,Oritsland O.Challenges in deep water experiments:Hybrid approach[J].Journal of Offshore Mechanics and Arctic Engineering,2002,124(2):90-96.

[2]Kendon T E.Ultra-deepwater model testing of a semi-submersible and hybrid verification[C].27th International Conference on Offshore Mechanics and Arctic Engineering,2008.

[3]Zhang H M,Sun Z L,Yang J M,Gao M Z.Investigation on optimization design of equivalent water depth truncated mooring system[J].Science in China Series G-physics Mechanics&Astronomy,2009,52(2):277-292.

[4]苏一华,杨建民,肖龙飞,李欣.基于静力相似的水深截断系泊系统多目标优化设计[J].中国海洋平台,2008,23 (1):14-19. Su Yihua,Yang Jianmin,Xiao Longfei,Li Xin.Multi-objective optimization design of truncated mooring system based on equivalent static characteristics[J].China Offshore Platform,2008,23(1):14-19.

[5]王宏伟,罗勇,苏玉民.悬链线式系泊与立管系统等效截断设计[J].哈尔滨工程大学学报,2010,32(12):1565-1572. Wang Hongwei,Luo Yong,Su Yumin.Equivalent truncation design of catenary mooring and riser system[J].Journal of Harbin Engineering University,2010,32(12):14-19.

[6]Udoh I E.Development of design tool for statically equivalent deepwater mooring systems[D].Texas:Texas A&M University, 2008.

[7]Baarholm R,Stansberg C T,Fylling I,Oritsland O.Model testing of ultra-deepwater floater systems:Truncation and software verification methodology[C].25th International Conference on Offshore Mechanics and Arctic Engineering, 2006.

[8]潘斌,高捷,陈小红,陈家鼎.浮标系泊系统的静力计算[J].重庆交通学院学报,1997,16(1):68-73. Pab Bin,Gao Jie,Chen Xiaohong,Chen Jiading.Static calculation of buoy mooring fast[J].Journal of Chongqing Jiaotong Institute,1997,16(1):68-73.

[9]韩凌,滕斌.Chebyshev多项式在海岸工程中的应用[C].第十七届全国水动力学研讨会暨第六届全国水动力学学术会议论文集,2003:822-829. Han Ling,Teng Bin.Application of Chebyshev phlynomic in the coastal engineering[C].Proceedings of the 17th National Conference on Hydrodynamics and 6th National Congress on Hydrodynamics,2003:822-829.

[10]郝春玲,滕斌.不均匀可拉伸单锚链系统的静力分析[J].中国海洋平台,2003,18(4):19-22. Hao Chunling,Teng Bin.Static analysis for a non-uniform flexible mooring cable system[J].China Offshore Platform, 2003,18(4):19-22.

[11]罗德涛,陈家鼎.锚泊定位系统的静力计算[J].船舶工程,1982,3:12-17. Luo Detao,Chen Jiading.Statics calculation of mooring positioning system[J].Ship Engineering,1982,3:12-17.

[12]王小平,曹立明.遗传算法:理论、应用及软件实现[M].西安:西安交通大学出版社,2002.

Optimized design of deepwater catenary mooring system in equivalent truncated water depth

FAN Tian-huia,b,QIAO Dong-shengb,OU Jin-pinga,b
(a.Faculty of Infrastructure Engineering;b.Deepwater Engineering Research Center, Dalian University of Technology,Dalian 116024,China)

Used in deepwater catenary mooring systems,the multi-component mooring lines are usually made up of three wire ropes and chains of different buoyancy unit weight,stiffness and length.Considering the gravity,tension,current force and mooring line extension,the piecewise extrapolating method is employed to the static analysis of the multi-component mooring line and the golden section method is used to find out the top angle of the mooring line.An optimized designing program is developed based on genetic algorithm considering the similarity of static characters for hybrid model test.Taking the catenary mooring system used for some semi-submersible platform of 1 500 m water depths for example,the equivalent truncated mooring system used in 700 m water depths is designed,which can provide references for the following processes in hybrid model test.

deepwater catenary mooring system;piecewise extrapolating method;hybrid model test; optimized design;equivalent truncated mooring system

P75

A

10.3969/j.issn.1007-7294.2015.05.006

1007-7294（2015）05-0518-08

2014-12-25

国家重点基础研究发展计划项目（973项目，2011CB013702；2011CB013703）；国家自然科学基金资助项目（51209037；51221961）；中国博士后科学基金特别资助项目（2013T60287）；中央高校基本科研业务费专项资金项目(（DUT14RC（4）30）

樊天慧（1987-），男，博士研究生，E-mail：fantianhui@mail.dlut.edu.cn；

乔东生（1983-），男，博士；

欧进萍（1959-），男，教授，中国工程院院士。