FPSO组合运动对锚泊阻尼影响研究

杨 勇，陈佳欣，尹 群

(江苏科技大学船舶与海洋工程学院，江苏镇江212003)

锚泊系统是限制海洋浮式结构物在某一固定范围之内移动并辅助其抵抗各种环境载荷的定位系统，精确的定位性能对于海洋浮式结构物而言是十分重要的［1］.海洋浮式结构物在复杂环境载荷的作用下，其往往会产生较为复杂的运动响应，其中，由于二阶慢漂波浪力的作用，结构物会产生大位移的低频振荡运动，同时由于该运动与结构物系统的固有频率较为接近，因此会产生大振幅的共振低频慢漂运动.文献［2］认为整个系统能够提供的阻尼是消耗能量、降低运动位移的主要因素之一，而海洋浮式结构物特别是船型浮式结构物在低频运动下其自身所能产生的纵荡方向阻尼十分有限，因此，系统阻尼中由锚泊系统提供的阻尼成为了决定低频运动响应的关键性因素.锚泊阻尼在结构物发生波频运动响应时，对浮体运动响应影响十分有限，但是对于低频运动，却影响很大，因为在一个低频纵荡运动周期内，锚泊线单元在垂直于其自身切线方向上运动的振幅远远大于平台自身的运动振幅.文献［3］中研究表明锚泊阻尼最大可以达到系统总阻尼的80%，由此可见，锚泊阻尼对海洋浮式结构物的低频运动响应的影响是举足轻重的.通常锚泊阻尼的计算方法可以分为:①准静态分析计算法;②时域动态有限元法;③模型实验法.其中，时域动态有限元法能够得到更加准确的结果，并且随着商业有限元软件的推广，在海洋工程界被广泛应用于锚泊阻尼的计算与研究中.

文献［4］中利用一种复杂的时域非线性完全动态有限元法并结合指示图法理论计算了锚泊线的顶端张力和锚泊阻尼，给出了无量纲参数分析研究.通过研究发现锚泊线的预张力对锚泊阻尼有着十分重要的影响.文献［5］中对15所大学与研究机构的有限元计算结果与实验进行了比较研究，发现时域分析有限元方法能够较为准确的得到锚泊线的顶端张力，从而得到更加准确的锚泊阻尼计算结果.文献［6］中对锚泊线轴向拉伸对锚泊阻尼的影响进行了研究，结果显示阻尼受其影响较大.鉴于准静态法在锚泊线处于半张紧状态或是顶端运动频率过高时，就会变得十分不准确，文中还是首选时域有限元法进行计算研究.文献［7］中利用受迫振动实验并结合指示图法对锚泊阻尼进行研究，实验结果与利用有限元软件模拟的结果十分吻合.

国内学者对锚泊阻尼的研究也有一定的成果.文献［8］中选取一组应用于实际工程中的锚泊参数，研究了各个参数对锚泊水平阻尼和垂向阻尼的影响.结果显示轴向刚度和顶端运动方程对锚泊阻尼的影响较为显著.文献［9－10］中用有限元方法进行非线性时域动力分析，分析了不同流速下的锚泊线动态响应，比较了锚泊线张力和锚泊阻尼，同时考虑了海底摩擦系数对锚泊阻尼的影响，认为海底摩擦引起的阻尼十分有限，流体动力阻尼还是锚泊阻尼的主要成分.文献［11］中分析了锚泊线预张力对FPSO系统动力效应的影响，对研究FPSO运动响应与锚泊阻尼的关系有一定的参考价值.

1 计算方法与理论

1.1 计算方程

锚泊线在顶端结构物一个纵荡运动周期内所消耗的系统能量E在数学上可以表示为锚泊线顶端水平张力和水平运动速度在该周期内的积分［4］:

式中:Th为锚泊线顶端张力水平分量;dX/dt为锚泊线水平运动速度;T为锚泊线顶端振荡周期.引入等效线性阻尼系数B，因此Th可以表示为:

将式(2)代入式(1)中，可以得到:

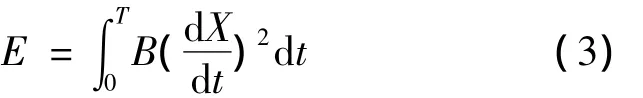
假设锚泊线顶端运动是周期为T、振幅为A的正弦振荡运动.解方程式(3)可以得到:

因此，可以得到等效线性阻尼系数:

从式(5)可以看出，得到锚泊线等效线性阻尼系数B的关键在于锚泊线所消耗能量值E的求解.

1.2 指示图理论

将锚泊线顶端水平运动位移X时历输入到有限元软件中，或者在有限元软件中进行直接定义，锚泊线顶端张力的水平分量Th通过有限元软件计算得到，并作为一个时间历程输出.将顶端张力水平分量与锚泊线顶端水平低频速度分量相乘，并在一个周期T内积分，得到锚泊线在一个周期内消耗的能量E.图1为利用指示图法求解消耗能量的流程，曲线围成的面积代表一个运动周期内锚泊线所消耗的系统能量.

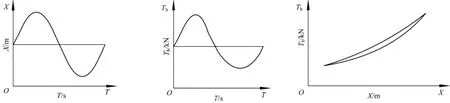
图1 用指示图法求解锚泊阻尼Fig.1 Indicator diagram method for calculating mooring line damping

2 锚泊线参数与环境参数

按照锚泊阻尼研究的标准形式，选取单根锚泊线为研究对象，水深为400 m，顶端结构物为FPSO，考虑其发生纵荡运动，锚泊线也沿着纵荡方向布置，计算中综合考虑锚泊线的流体动力阻尼与海底摩擦阻尼.利用OrcaFlex软件，根据悬链线方程计算找到锚泊线初始平衡形态，作为动态计算的起始点.锚泊线是混合式金属锚泊线，两端为钢链，中间为钢索，这也是现今使用最广泛的金属锚泊线形式.主要环境参数和锚泊线参数分别如表1，2所示.

表1 环境参数Table 1 Environmental condition

表2 锚泊线参数Table 2 Parameters of the mooring line

3 计算结果及分析

3.1 波频运动对锚泊低频阻尼的影响

以振幅为30m、周期为300s的低频正弦运动为基础运动，叠加两组波频正弦运动，一组进行振幅上的改变，一组进行周期上的改变.各种工况下锚泊线顶端的最大水平张力、能量耗散值以及等效线性阻尼系数在表3给出了具体数值.从表3结果可以发现，在叠加波频运动后，锚泊线的顶端最大水平张力、能量耗散值以及等效线性阻尼系数均变大，并且波频运动的振幅越大、周期越短，所增加的程度越大.

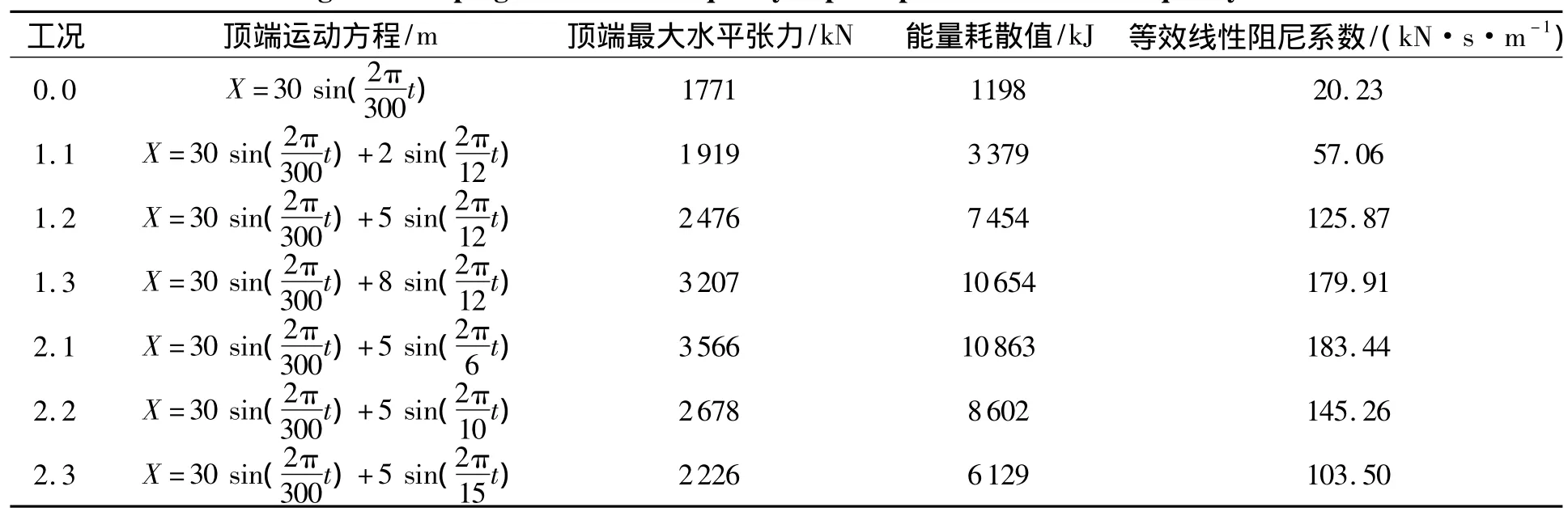
表3 低频正弦与波频正弦组合运动的锚泊阻尼Table 3 Mooring line damping due to low-frequeney superimposed with wave-frequency sinusoidal motion

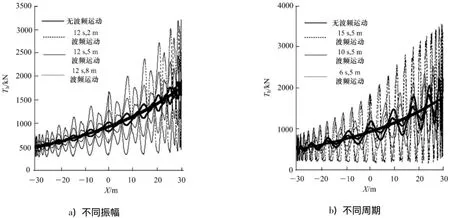
图2 波频运动不同振幅、不同周期锚泊阻尼指示Fig.2 Indicator diagram for various amplitudes and periods of wave-frequency motion

图2为两组工况的阻尼指示图，分别以锚泊线顶端张力的水平分量Th和锚泊线水平位移的低频成分X为纵坐标和横坐标绘制曲线，曲线所围成的面积即一个低频运动周期内锚泊线所消耗的系统能量.从图中可以发现，随着波频运动振幅A的增加，锚泊线张力峰值会变大，随着波频运动周期T的减少，锚泊线张力波动会更加剧烈，以上两种情况均会导致耗散能量的增加.图3为锚泊阻尼B与叠加波频运动的振幅A和周期T之间的关系，可以看出锚泊阻尼随波频运动幅值的增加而增加，随波频运动周期的增大而减小.

图3 波频运动振幅与周期对锚泊阻尼的影响Fig.3 Influence of amplitude and period of wave-frequency motion on mooring line damping

3.2 波频运动对不同锚泊低频阻尼的影响

在上文中，仅仅以振幅30m、周期300s的低频运动为基础运动进行研究分析，考察加入波频运动对锚泊阻尼的影响.为了更为全面地进行分析，下面针对几个不同的低频运动进行叠加波频运动后的对比研究，计算工况与结果如表4所示.

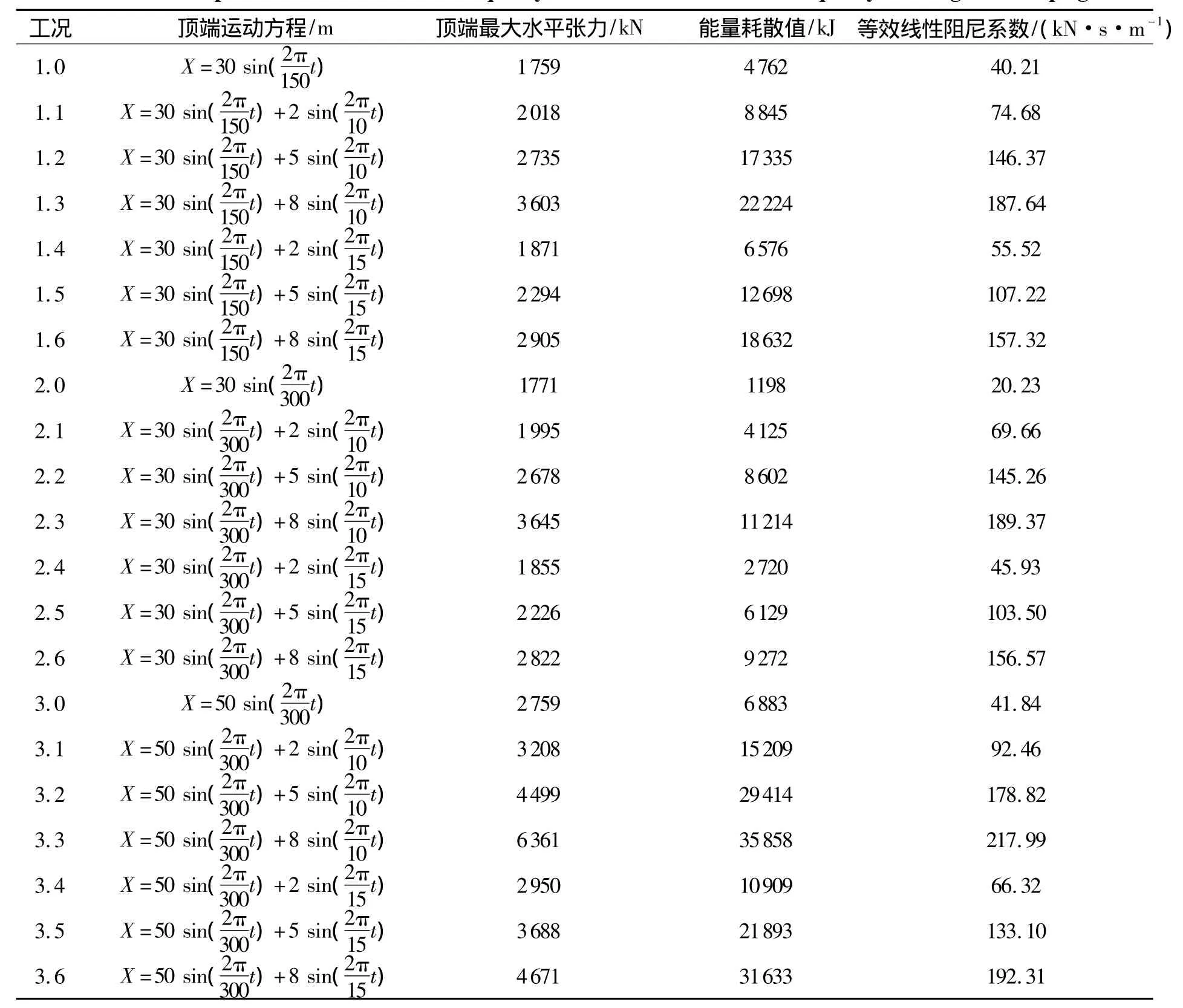
表4 波频运动对不同锚泊低频阻尼影响的比较Table 4 Comparison on effect of wave-frequency motions on different low-frequency mooring line damping

图4为叠加的波频运动周期T为10，15s时，振幅A分别为2，5，8m时的锚泊线等效线性阻尼系数B变化趋势.在低频运动振幅为30m、周期为150s情况下，当叠加的波频运动振幅为8m，周期分别为10，15s时，锚泊线阻尼分别扩大4.7，3.9倍.类似的，在低频运动振幅为30m、周期为300s情况下，当叠加的波频运动振幅为8m，周期分别为10，15s时，锚泊线阻尼分别扩大9.4，7.7倍.在低频运动振幅为50 m、周期为300 s情况下，当叠加的波频运动振幅为8 m，周期分别为10，15s时，锚泊线阻尼分别扩大5.2，4.6倍.从图中可以发现两个关键的特征:①当波频运动周期为10 s时，锚泊线的阻尼增长是非线性的，但是当周期为15s时，增长趋势几乎变为线性的;②单一低频运动振幅为30m、周期为150s，以及单一低频运动振幅为50m、周期为300s时，所对应的锚泊低频阻尼值十分相近，但是，随着叠加波频运动振幅的增加，两者之间的差别会越来越大.相反，单一低频运动振幅为30m、周期为150s和单一低频运动振幅为30m、周期为300s时，两者所对应的锚泊低频阻尼是不同的，但是随着叠加波频运动振幅的增加，两者之间会越来越趋于相近.可以看出波频运动成为决定锚泊阻尼大小的关键性因素.

图4 不同波频运动振幅下锚泊阻尼变化过程Fig.4 Mooring line damping vs.wave-frequency motion amplitude

3.3 流速的影响

海底流速分别选择0.5，1.0，1.5 m/s，加上无流速，总共4组工况16个算例研究流速对锚泊阻尼的影响.设计工况和结果如表5所示，前两组工况为单一低频正弦运动，后两组工况为低频正弦运动与波频正弦运动的组合运动，以此进行比较研究，叠加的波频正弦运动振幅为5m，周期为10s，流速方向与锚泊线布置方向在同一平面内.

表5 流速对锚泊阻尼的影响Table 5 Effect of current on mooring line damping

图5为不同流速下的锚泊阻尼指示图，图6为锚泊阻尼B随着流速vs变化的关系图.当锚泊顶端运动为单一低频运动时，流速变化对锚泊阻尼有显著影响，随着流速的增加，锚泊阻尼呈现非线性增长.工况组1中，最大流速情况下，锚泊阻尼比无流速状态下锚泊阻尼扩大了2.4倍.工况组2中，最大流速情况下，锚泊阻尼比无流速状态下锚泊阻尼扩大了2.0倍.对于组合运动而言，工况组3和工况组4中最大流速情况下锚泊阻尼比无流速状态下锚泊阻尼扩大了1.1倍.随着流速的增加，锚泊阻尼显示出近似线性增长，但是增长幅度十分有限.可以总结出，波频运动存在的情况下，流速对锚泊阻尼的影响将被弱化，波频运动占主导地位，决定锚泊阻尼值的大小.在Webster的研究中，当顶端运动频率处于波频范围内时，流速对锚泊阻尼的影响也十分有限.

图5 不同流速锚泊阻尼指示

图6 不同流速下锚泊阻尼变化过程Fig.6 Mooring line damping vs.current speed

3.4 锚泊线预张力的影响

当锚泊线预张力较大时，锚泊线会处于张紧状态，弹性伸缩力是回复力的主要贡献，当锚泊线预张力较小时，锚泊线处于松弛状态，惯性力是回复力的主要贡献.预张力分别选择1174，1574，1974，2374，2774kN.总共两组工况10个算例，设计工况和结果如表6所示.其中工况组1为单一低频正弦运动，工况组2为低频正弦运动与波频正弦运动的组合运动，低频运动的振幅为30m，周期为150 s，叠加的波频正弦运动振幅为5m，周期为10s.

表6 锚泊线预张力对锚泊阻尼的影响Table 6 Effect of pre-tension on mooring line damping

图9为不同锚泊线预张力下的锚泊阻尼指示图，图10为锚泊阻尼B随着预张力F变化的关系图，随着锚泊线预张力的增加，锚泊阻尼呈非线性上升的趋势.工况组1中，最大锚泊阻尼是最小锚泊阻尼的7.9倍;工况组2中，最大锚泊阻尼是最小锚泊阻尼的6.3倍，增长均十分显著.工况组1与工况组2的增长趋势没有太大区别，说明无论是单一低频运动还是组合运动，锚泊线预张力对锚泊阻尼的影响是相似的.

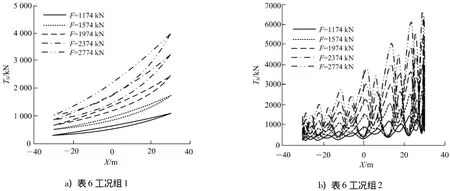
图7 不同预张力锚泊阻尼指示Fig.7 Indicator diagrams for various pre-tensoins

图8 不同锚泊线预张力下锚泊阻尼变化过程Fig.8 Mooring line damping vs.pre-tension

4 结论

1)在锚泊线顶端结构物运动中叠加入波频运动后，锚泊阻尼会大幅度增长，并且随着波频正弦运动振幅和频率的增加，锚泊阻尼还会呈现进一步上升趋势.同时，在低频正弦运动与波频正弦运动的组合运动下，低频运动方程改变对锚泊阻尼的影响几乎可以忽略，不同低频运动对应不同的低频锚泊阻尼，在叠加入相同波频运动后，锚泊阻尼值趋于相近.

2)当顶端运动是低频正弦运动时，流速改变对锚泊阻尼的影响比较显著，锚泊阻尼随着流速增加而变大，当顶端运动是组合运动时，流速改变对锚泊阻尼的影响变的很小，几乎可以忽略;无论顶端运动是低频正弦运动或是组合运动，锚泊线预张力对锚泊阻尼的影响都十分显著，锚泊阻尼随着预张力增加而变大.

References)

［1］ Faltinsen O M.Sea loads on ships and offshore structures［M］.UK:Cambridge University Press，1999:257－264.

［2］ Huse E.Influence of mooing line damping upon rig motions［C］∥18th Offshore Technology Conference.Houston USA:［s.n.］，1986:433 －438.

［3］ Huse E，Matsumoto K.Mooring line damping due to first and second order vessel motion［C］∥21st Offshore Technology Conference.Houston USA:［s.n.］，1989:135 －148.

［4］ Webster W C.Mooring-induced damping［J］.Ocean Engineering，1995，22(6):571 －591.

［5］ Brown D T，Mavrakos S.Comparative study on mooring line dynamic loading［J］.Marine Structures，1999(12):131－151.

［6］ Johaning L，Smith G H，Wolfram J.Measurements of static and dynamic mooring line damping and their importance for floating WEC devices［J］.Ocean Engineering，2007(34):1918－1934.

［7］ Kitney N，Brown D T.Experimental investigation of mooring line loading using large and small-scale models［J］.Offshore Mechanics and Arctic Engineering，2001(123):1－9.

［8］ 苏志勇，陈刚，杨建民，等.深海浮式结构物锚泊阻尼参数研究［J］.海洋工程，2009，27(2):21－28.Su Zhiyong，Chen Gang，Yang Jianmin，et al.Study on deepwater floating structure mooring line damping parametes［J］.The Ocean Engineering，2009，27(2):21 －28.(in Chinese)

［9］ 乔东升，欧进萍.深水悬链锚泊线粘性阻尼计算［J］.海洋工程，2009，27(4):16－22.Qiao Dongsheng，Ou Jinping.Calculation on viscous damping of deepwater catenary mooring line［J］.The O-cean Engineering，2009，27(4):16 －22.(in Chinese)

［10］ 乔东升，欧进萍.深水悬链锚泊线阻尼计算［J］.振动与冲击，2011，30(2):24－31.Qiao Dongsheng，Ou Jinping.Damping calculation of a deepwater catenary mooring line［J］.Journal of Vibration and Shock，2011，30(2):24 －31.(in Chinese)

［11］ 王志东，刘晓健，陈剑文.FPSO系泊系统参数的动力效应影响分析［J］.江苏科技大学学报:自然科学版，2013，27(5):409－418.Wang Zhidong，Liu Xiaojian，Chen Jianwen.Analysis of the influence of mooring system parameters on dynamic response of FPSO system［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2013，27(5):409 －418.(in Chinese)