考虑船舶航速的集装箱班轮燃油补给策略
饶明君,杨 斌,朱小林,许波桅
(上海海事大学物流研究中心,上海201306)
随着国际贸易的迅速发展,海运已经成为重要的国际运输方式.在国际运输船舶的3种营运方式之中,班轮运输在最近的几十年中显著增加.由于全球金融危机,2008~2009年班轮航运业增速有所放缓,但在2014年则有很大的反弹.目前航运公司所面临的主要挑战是如何在船用燃油价格上涨和波动的大环境中降低船用燃油消耗成本.
近年来,船用燃油成本大幅增加,甚至超过航运公司总运营成本的一半.文献[1]指出当船用燃油价格约为每吨500美元时,船用燃油成本约占大型集装箱船营运成本的3/4,因此降低船用燃料成本可以大量节省总运营成本.文献[2]研究集装箱运输在高燃油成本的影响下班轮服务配置问题,设计了一个成本模型来模拟燃油成本变化对班轮运营成本的影响.文献[3]提出对船用燃油成本实行事先、事中以及事后管理的理念以降低航运公司在运营过程中的燃油成本.文献[4]针对海上航行时间的不确定性,以最小化航行成本和预期的燃料成本为目标,建立非线性混合整数规划模型.文献[5]针对各沿海港口作业时间的不确定性,优化班轮时间表,使得班轮运输路线的总燃油消耗量减少.随着原油价格的不断攀升,造成船舶油耗成本增加,采用减速航行来降低船舶油耗成本的策略应运而生,文献[6]设计船舶燃油补给方案,研究燃油消耗与航速之间的关系,说明船舶以最佳航速运行可降低燃油成本.文献[7]研究固定航线的船用燃油消耗最小化问题,通过时间窗优化船舶在航线上的速度.然而,低转速航行会造成航线配船数量的增加,势必导致船舶与航次的固定成本增加.
上述多数研究忽略了集装箱班轮运输中的相互关联性,只对部分问题进行优化.文中基于文献[8]提出的船舶油耗计算公式,在单航线多航次的集装箱班轮运输中考虑船舶航速影响,并最终建立关于船舶航速的燃油相关总成本最小模型,从而得出较合理的燃油补给策略.
1 问题描述
从文献研究中可知油耗和船舶速度有关,一般而言,单位时间的油耗f主要由船舶速度v决定,油耗与船舶速度呈正相关,在文献[9]中,采用简单的线性回归方程.
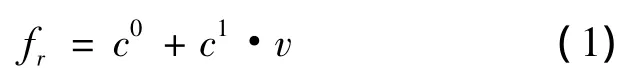
式中c0和c1是回归系数.
文献[10]的研究中表明船舶的油耗不仅与速度有关,与船舶大小类型也有关,所以上述线性回归方程不能够精确计算油耗.在文献[8]的研究中,单位时间里的油耗采用
式中μ的值与船舶大小型号有关.根据文献[8]采用的油耗计算公式,每条航段r的船舶油耗Fr可以表示为单位时间里的油耗乘上航行时间
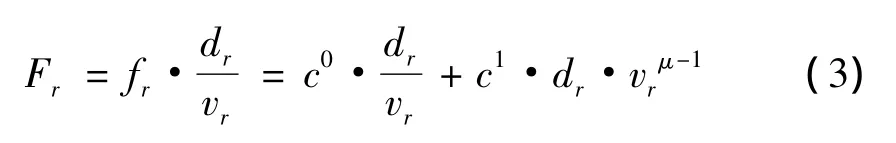
式中:dr为航段r的路程长度,vr为航行在航段r上的速度.
为了呈现油耗和速度之间的关系,对船舶油耗表达式(3)求关于速度的一阶导数和二阶导数.
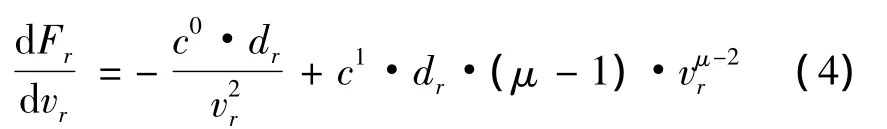
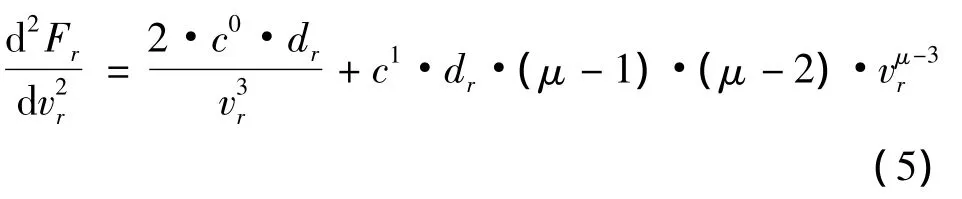
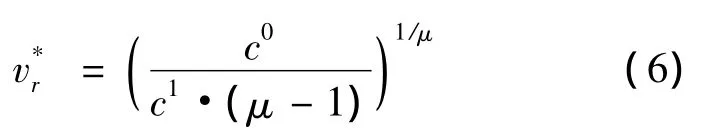
在集装箱班轮运输中,航运公司首先要确定一次燃油补给只满足下一个航次的运输需要,还是满足未来多个航次的需要,燃油补给量的大小直接影响船舶的载重能力,过多的燃油补给量会减少船舶的运载量,降低航次运营收益.其次,船舶航速直接影响燃油消耗量,进而影响燃油补给时间和燃油补给量的决策.各因素之间的关系如图1.
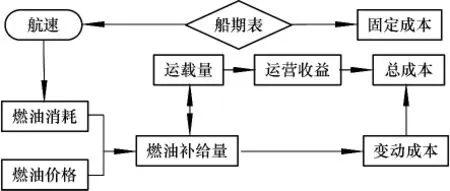
图1 班轮燃料补给相关因素关系Fig.1 Relation of factors
2 模型的建立
2.1 模型参数
下面定义相关参数、决策变量与因变量.
参数变量:dij表示港口i到港口j的路径长度;n表示船舶挂靠港口的数量;t表示船舶往返总航行时间(h);ti表示船舶在港口i的停泊时间,包括抵港时间、装卸时间、闲置时间和出港时间;ei表示允许船舶抵港最早时间;li表示允许船舶抵港最晚时间;ai表示船舶在港口i停泊时的耗油量;φ表示船舶加油的固定成本;h表示船舶单位燃油库存持有成本;w表示船舶燃油舱的最大容量;Vmin与Vmax分别表示船舶最低与最高档次航速(knots);q表示船舶最大加油次数表示收益损失系数,分别表示船舶在港口i的单位燃油价格及折扣价格,且
决策变量:vi,j表示船舶从港口i航行至港口j的航速;Si表示船舶在港口i的燃油安全库存量(t);Bi表示安排船舶在港口i加油则为1,否则为0;α1i,…表示港口i的分段燃油价格折扣系数;β1i,…表示港口i的分段燃油成本函数0-1变量.
因变量:Ii表示在船舶港口i的船舶燃油舱剩余油量(t);Ci表示在船舶港口i的燃油补给成本(USD);Fi,j表示船舶从港口i到港口j的耗油量(t);Ai表示船舶抵达港口i的时间(h).
港口船用燃油供应商为获取更多利润,将根据加油量提供分段折扣价格优惠.船舶在港口i的燃料补给成本为:
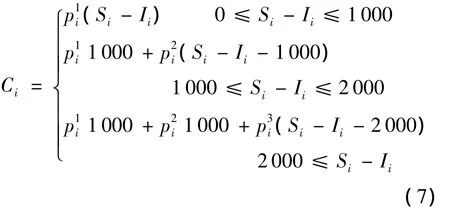
2.2 数学模型
以周计划内船舶燃油相关总成本最小,建立与船舶航行速度有关的混合整数非线性规划模型.固定的班轮航线路径长度已知,航速决定船舶在该条航段的航行时间及燃油消耗.
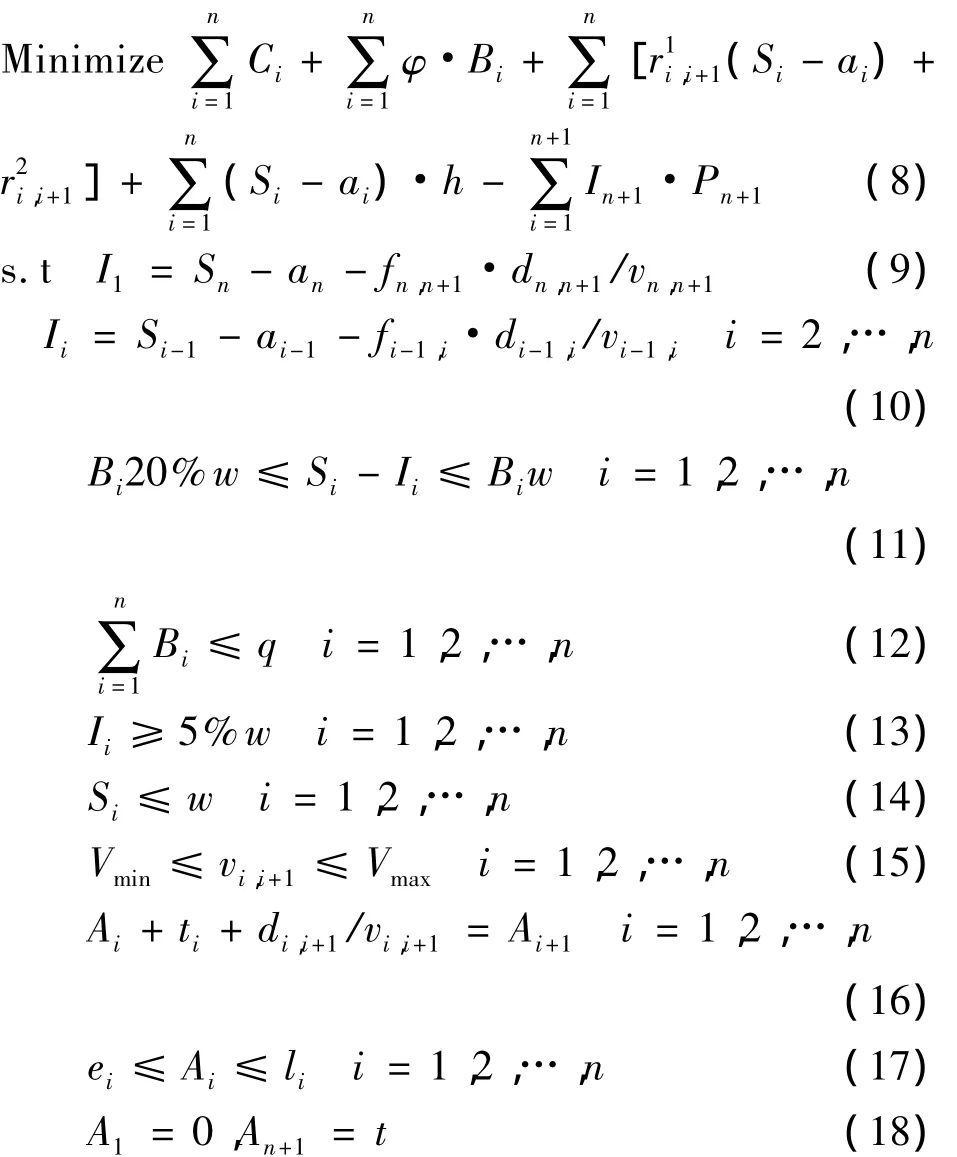
通过式(8)定义目标函数的构成,第一部分是燃油消耗变动成本;第二部分是船舶加油固定成本;第三部分是船舶在离开港口时由于燃油载重而损失的运营收益;第四部分是船舶燃油库存持有成本;第五部分是船舶返回始发港时燃油剩余量的收益.式(9,10)根据上次航次燃油补给情况计算出本航次船舶燃油舱剩余油量;式(11)表示加油量占船舶油舱容积比的限制;式(12)表示船舶最大加油次数的上限;式(13)确保船舶燃油剩余量始终保持在一定的最低库存水平;式(14)确保船舶燃油的安全库存量不能超过油舱容积;式(15)表示船舶航速范围限制;式(16)表示船舶航行的时间流守恒方程;式(17)表示船舶抵达港口的时间窗约束;式(18)表示船舶完成整个循环航线后返回始发港的总航行时间.
3 模型求解
为了避免凸函数的连续性对模型求解带来的复杂性,文中利用分段线性逼近函数来近似表达关于船舶航速vi,i+1的非线性燃油成本函数,现证明如下:

图2 线性化几何图Fig.2 Linerization of function
如图2,F(x)表示一个单变量函数,坐标X1,X2,…,Xn表示n个用于分段近似的间断点.对两个相邻 间 断 点 [(Xi,F(Xi)),(Xi+1,F(Xi+1))] 和[(Xi,F(Xi)),(Xi+1,F(Xi+1))]之间的函数进行线性化,其中i=1,2,…,n-1.对任意,Xi≤≤Xi+1,其函数值可由F(Xi)和F(Xi+1)的凸组合近似表示.假定λ∈[0,1],那么可由式(19)导出,而其近似值F),fα)可由式(20)求出.采用斜率(F(Xi+1)-F(Xi))/(Xi+1-Xi)描述时,得到式(21),其中λ=(Xi+1-)/(Xi+1-Xi).
为每一个间断点引入一个连续变量αi,并且αi∈[0,1](i=1,2,…,n).而 βi是一个0~1 变量,对应于第i区间[xi,xi+1](i=1,2,…,n)且 β0=βn=0α可由式(22~26)的约束条件求得:
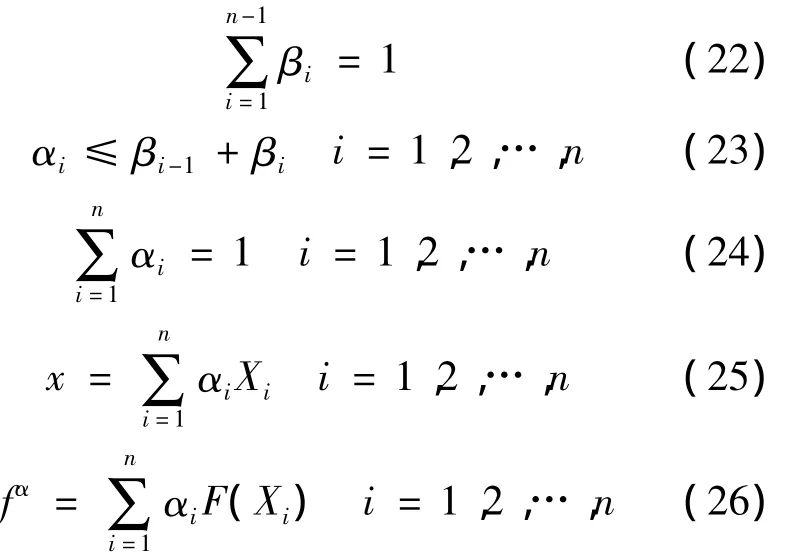
式(22)表示对于任意i来说,只有一个区间βi能够取值为1.式(23)表示 αi为 αi-1或 αi+1,且不为 0,并满足式(24)和(25),即 αi-1=λ 和 αi+1=1-λ.式(26)确保根据式(20)求得近似值.
式(22~26)可以简化特殊有序集约束.定义一组变量成为特殊有序集k(SOSk),有序集的元素能取非零值,但必须是相邻的.大多数混合整数线性规划求解器能够自动处理类型1和2的特殊有序集.
文中将折扣系数α定义为SOS2变量,利用此方法将非线性的燃油成本函数转化为线性成本函数.设wi,i+1=1/vi,i+1,i=1,2,…,n,即上述 MINLP模型等价于下列MILP模型:


目标函数式(27)以周计划内船舶燃油补给相关总成本最小;式(28,29)表示燃油成本的分段线性化函数;式(31,32)表示船舶燃油消耗与速度的函数关系式;式(33)表示wi,i+1的区间范围;式(34)表示船舶航行时间流守恒方程.
4 实例分析
以某航运公司的亚洲—欧洲航线(AEX)为例,说明如何利用上述数学模型与算法制定船舶燃油补给合理方案.如图3,该航线包含了15个挂靠港.在该航线上,共部署9艘集装箱班轮来提供单周班服务.表1为船舶相关参数取值其中,φ=1000,h=50,μ =3.
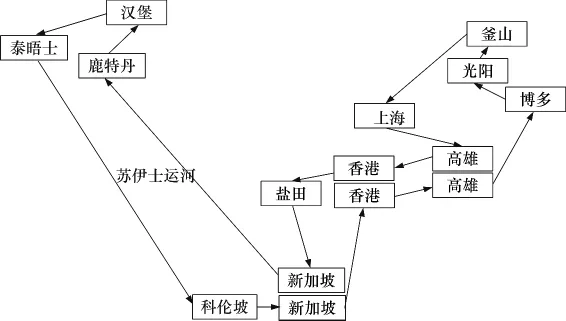
图3 亚欧航线Fig.3 Asia-Europe express service route
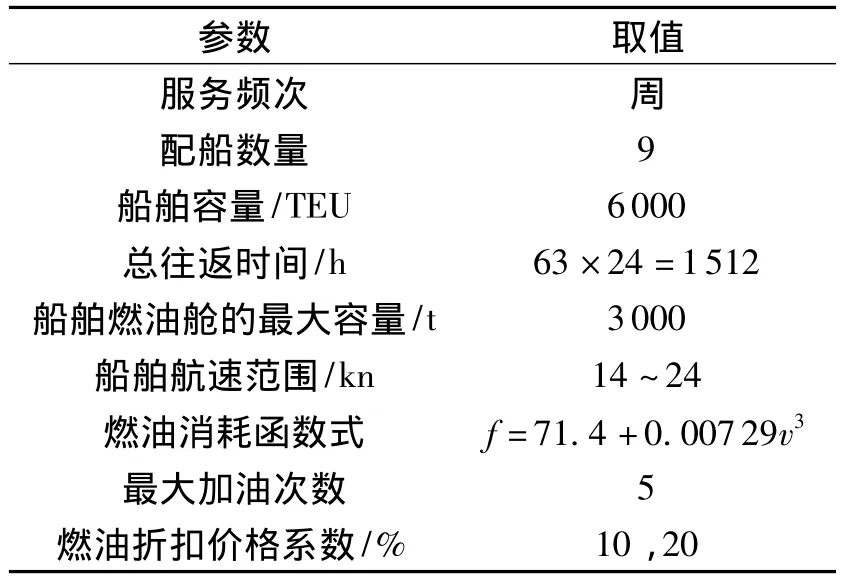
表1 亚欧航线相关参数Table 1 Parameters for AEX service
4.1 港口时间窗的对比分析
在集装箱班轮运输中,港口时间窗约束是普遍存在的,它要求船舶必须在规定的时间内到达特定的港口,港口运营商将根据抵港船舶信息制定合理的泊位——岸桥计划.基于固定的燃油价格、航行总时间和可靠泊加油的港口前提下,文中对比了两种场景:带时间窗约束和不带时间窗约束,并且假设不带时间窗约束的情况下没有额外惩罚成本.图4说明了两种场景下的船舶燃油补给港与航速变化关系,可以发现不带时间窗约束的场景下船舶航速基于21kn上下浮动,燃油成本是3162360 USD;而相对于带时间窗约束下船舶航速却高达23.1 kn,燃油成本比前者多了14030 USD.由此可见,航运公司可以在保持总航行时间不变的情况下调整到达港口的时间窗从而使运营收益最大化.总成本减小原因主要有以下两种:①总加油量从6537.8 t减少到6506.8 t;②有时间窗约束时,船舶需要在4个港口进行加油,而没有时间窗的场景下只在3个港口需要加油.此外,由于船速的不同导致了到达每个港口的时间节点也不同,如表2.
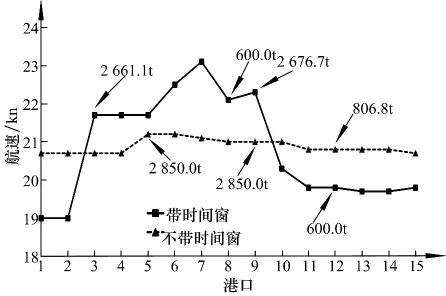
图4 两种情况下的船舶燃油补给策略Fig.4 Vessel′s efueling strategy under two scenarios
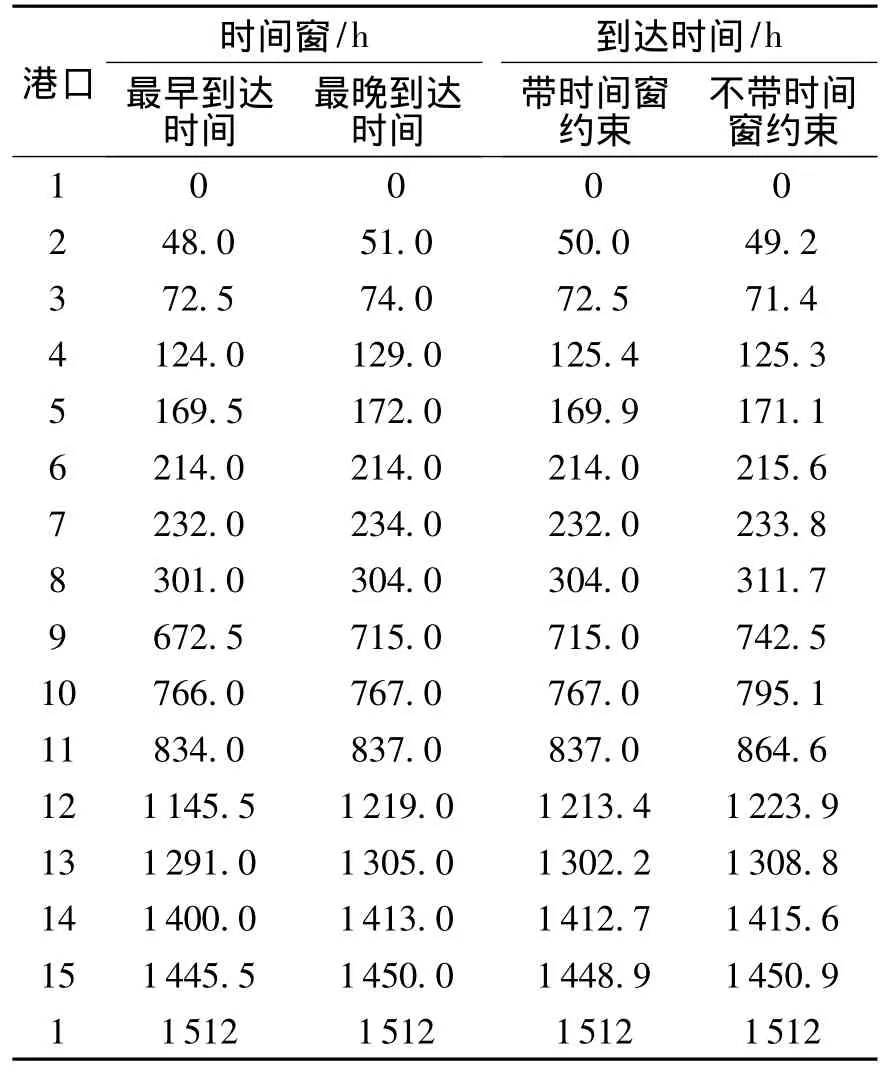
表2 带时间窗约束和不带时间窗约束场景下实际到达港口时间Table 2 Port arrival windows and actual arrival times for AEX(with/without port arrival time windows)
从整体来看,带时间窗约束下迫使船舶通过调整航速来满足港口作业要求,而船舶加速将直接导致船舶总油耗的增加,然而不同航段的油耗增量变化趋势是起伏不定的,有些航段油耗的增量并不是和速度增加呈正比,原因是船舶油耗和船舶类型的选择存在一定的关联性,选择更大类型的船舶,从而使加油港的选择不同,相应的油耗成本也会增加.
4.2 燃油价格的敏感性分析
由于燃油价格随时间频繁波动,而海上运输周期较长,因此船舶在挂靠港的燃油补给计划成为船公司面对的重要决策问题.文中在可供靠泊加油的港口前提下,考虑了5种场景来研究燃油价格变化对补给策略的影响:①所有可加油港口的燃油价格相同,都为510 USD/t;②沿着航线依次提高燃油价格;③沿着航线依次降低燃油价格;④沿着航线先提高再降低燃油价格;⑤沿着航线先降低再提高燃油价格.为了在同等水平下进行比较,将所有可供加油港口的基准燃油价格都设为510 USD/t.上述五种场景下最佳燃油补给策略和燃油相关总成本的运行结果分别由表3与图5所示.
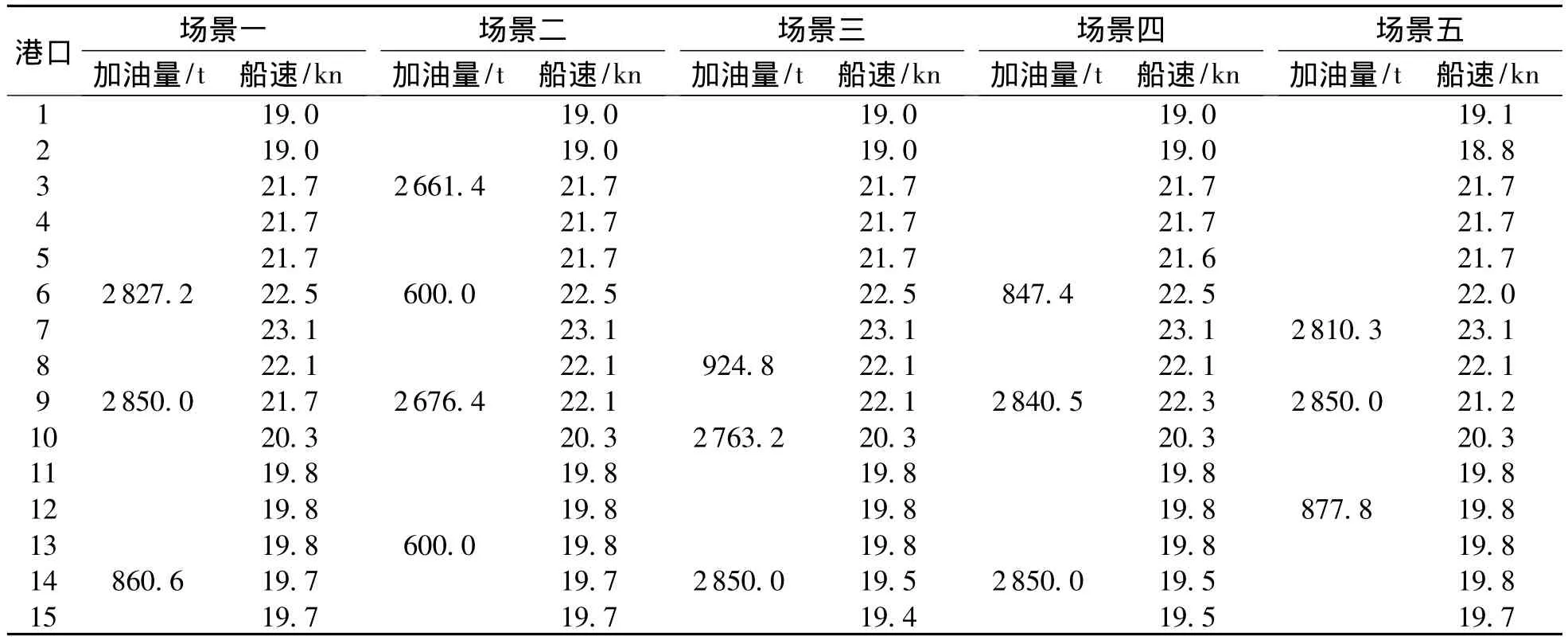
表3 不同价格场景下船舶燃油补给策略Table 3 Optimal bunker fuel strategies at different price scenarios
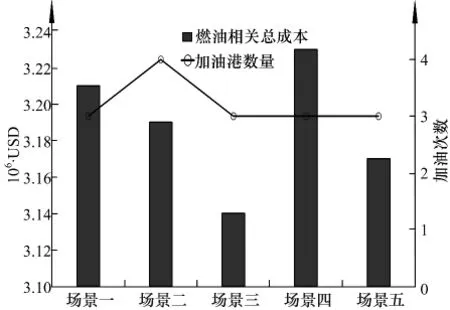
图5 不同场景下的燃油总成本与加油次数Fig.5 Bunker fuel cost and bunkering times at different price scenarios
从表3和图5中可知,虽然基准燃油价格相同,但是不同的燃油价格变化会导致不同的燃油补给方案和总成本,场景四的燃油成本为3232330 USD,比最低燃油成本的场景三多89710 USD;同时,除了在场景二下船舶加油4次之外,其它场景都为3次.从最后3种场景不难发现,燃油价格最低的港口不一定就是最优的加油港口,这主要原因是船舶在不同的港口有不同的燃油补给需求,同时有些港口提供价格折扣优惠策略.
此外,由于该模型考虑了港口时间窗约束,在5种场景下船速的差异并不显著,只是局部的微调整.由此可见,班轮服务中的燃油价格变化影响着加油港口的选择,而港口时间窗约束则影响着船舶航速的调整.
4.3 船舶油舱容量影响分析
表4说明了在两个不同油舱容量下的船舶燃油补给策略.从表中可知,如果将船舶油舱容量从3000t增加到4000t,船舶加油港数量将从4个减少到2个,燃油相关总成本从3 176 390 USD降低到3063980USD,减少幅度将近3.54%.虽然油舱容量增加燃油成本会减少,但是由于可装载集装箱量减少而出现收益损失,所以航运公司在船舶油舱容量选择上必须寻求燃油成本与收益损失之间的平衡.
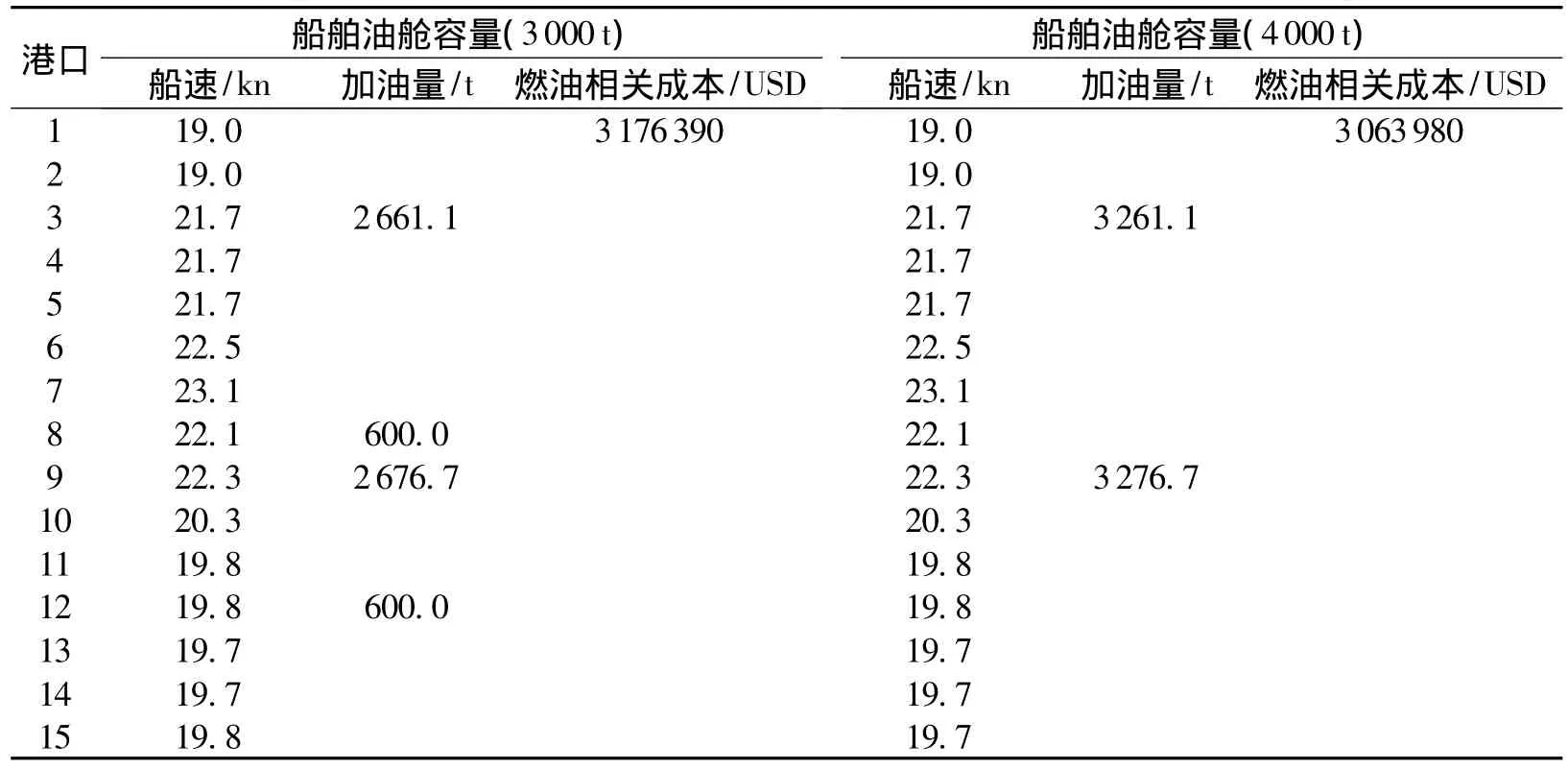
表4 不同船舶油舱容量下燃油补给策略Table 4 Optimal bunker fuel management strategies at different bunker fuel capacities
4.4 船舶类型影响分析
在集装箱班轮航线配船计划中,航运公司需要依据不同航线特点来部署相应的船舶类型,而船舶类型决定了船舶燃油消耗与航速调整.在保持燃油价格、油舱容量相同等其它因素前提下,文中对比分析3000TEU与5000 TEU的最优航速策略(图6),从图中可知,由于两者均考虑港口时间窗约束,所以使得船舶在各航段的最优航速出现较大波动,表明该模型具有调整船舶航速的能力.

图6 不同类型船舶的最优航速策略Fig.6 Optimal speed strategies at different ships
4.5 航线变化下燃油补给策略
由于班轮航线上的挂靠港口可能受港口拥堵、台风海啸等不确定性因素的干扰影响,航运公司往往就需要做出有效的船期恢复措施,其中主要以取消该港口挂靠、改变挂靠港顺序两种方案为主.文中假设汉堡港受可预见的港口拥堵而导致该港口的临时关闭场景,在已知船期表变化基础上研究船舶燃油补给策略(表5).
因为取消汉堡港的挂靠直接导致航线总距离的缩短,所以将原始航线与取消汉堡港的新航线进行对比分析.文中的两种场景下都不考虑港口时间窗约束,并且始终保持船舶总航行时间不变.从表5中可知,如果取消汉堡港挂靠,船舶燃油相关成本将从3162360USD减少到3012700USD,这主要是因为到达所有港口的速度降低,从而减少船舶燃油消耗.然而,取消汉堡港势必导致失去在汉堡港装卸集装箱的收益.因此,船舶在选择加油港时,只有当降低的成本远远超过收益损失时,这种策略才符合成本效益.

表5 航线变化下燃油补给策略Table 5 Optimal bunker fuel management strategies at different routes
5 结论
文中从运营者角度进行单航线集装箱班轮运输的船舶燃油补给问题研究,创新性地将加油港的选择、加油量的确定及航速的调整进行整体优化,建立混合整数非线性规划模型,并引用分段线性逼近函数将其近似的表达为线性函数后用Cplex进行求解,最后通过某航运公司的亚洲—欧洲航线实例对模型进行仿真实验.通过算例表明,从整体上归纳有3点:①为了最小化燃油总成本,将加油港、加油量和船速整体优化具有非常重要的现实意义,因为三者之间相互关联,相互影响;②燃油价格变化趋势是选择加油港口的重要因素,不同的价格趋势将会导致不同的燃油补给策略;③在保持总航行时间不变的情况下,优化现有的时间窗约束可以改变抵达港口的时间和航速,进而大幅度的降低船舶油耗.从细节上归纳有两点:①船舶油舱的最大容量增加能够带来显著的燃油成本节约效果,航运公司可以将其考虑在船舶部署和新船建造中;②在航线中取消一些港口挂靠可以减少航线总距离,进而减小航速和燃油消耗.有些航运公司已经采用这种方法来降低燃油成本.
今后可在以下两个方面继续进行后续研究:
1)将不确定性引入模型.这些不确定性因素可能包括燃油价格波动、天气突变、船舶故障、港口拥堵等;
2)减少环境污染.在环境问题越来越受关注的今天,人们意识到船舶温室气体排放的重要性,如何制定有效的减排措施与政策是下一步努力方向.
References)
[1] Ronen D.The effect of oil price on containership speed and fleet size[J].Journal of the Operational Research Society,2011,62(1):211-216.
[2] Notteboom TE,Vernimmen B.The effect of high fuel costs on liner service configuration in container shipping[J].Journal of Transport Geography,2009,17(5):325-37.
[3] 刘天芸.航运企业船舶燃油成本管理[J].世界海运,2007,29(6):36-37.Liu Tianyun.Shipping fuel cost management of shipping companies[J].Journal of the World Shipping,2007,29(6):36-37.(in Chinese)
[4] Wang Shuaian,Meng Qiang.Liner ship route schedule design with sea contingency time and port time uncertainty[J].Transportation Research Part B,2012,46(5):615-633.
[5] Qi Xiangtong,Song Dongping.Minimizing fuel emissions by optimizing vessel schedules in liner shipping with uncertain port times[J].Transportation Research Part E,2012.48(4):863-880.
[6] 黄涛.船舶运输成本分析与控制[D].大连:大连海事大学,2002:23-40.
[7] Fagerholt K,Laporte G,Norstad I.Reducing fuel emissions by optimizing speed on shipping routes[J].Journal of the Operational Research Society,2010,61(3):523-9.
[8] Du Yuquan,Chen Qiushuang,Quan Xiongwen,et al.,Berth allocation considering fuel consumption and vessel emissions[J].Transportation Research Part E,2011,47(6):1021-1037.
[9] Niels Lang,Albert Veenstra.A quantitative analysis of container vessel arrival planning strategies[J].OR Spectrum,2010,32(3):477-499.
[10] Hulskotte J H J,Denier van der Gon H A C.Fuel consumption and associated emissions from seagoing ships at berth derived from an on-board survey[J].Atmospheric Environment,2010,44(9):1229-1236.

