不同类型锚泊方式对深水浮式平台的阻尼贡献比较计算
乔东生 , 樊天慧 , 欧进萍 ,
(1大连理工大学 深海工程研究中心,辽宁 大连 116024;2大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
不同类型锚泊方式对深水浮式平台的阻尼贡献比较计算
乔东生1, 樊天慧2, 欧进萍1,2
(1大连理工大学 深海工程研究中心,辽宁 大连 116024;2大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
锚泊阻尼对深水浮式平台的运动响应具有重要贡献。利用单根锚泊线由于上部浮体运动而产生的能量耗散原理计算锚泊阻尼。分别采用准静定计算方法和非线性动力有限元时域分析方法,针对三种具有相似静恢复力刚度,但不同类型的锚泊系统:悬链式、张紧式和半张紧式,对其锚泊阻尼贡献进行比较计算。该结果给出了不同锚泊阻尼计算方法的适用范围,并对不同锚泊方式的阻尼贡献进行了总结。
锚泊类型;阻尼贡献;准静定;时域分析
1 引 言
锚泊阻尼在预测浮式平台的运动响应中是一个很重要的因素,一般可以定义为锚泊线随上部浮体运动所消耗的能量[1]。有研究表明,锚泊阻尼最大可以达到浮式结构物系统总阻尼的80%左右。许多学者研究了浮式结构物及其锚泊系统的动力性能,表明锚泊阻尼对浮式结构物的运动性能具有显著的影响[2-3]。
目前,锚泊阻尼的具体计算方法主要有三种:模型试验方法、准静态简化计算方法、非线性有限元动力计算方法。因为受到模型水池的宽度和深度、缩尺效应等条件限制,面对适用于深水的锚泊系统直接利用模型试验得到其锚泊阻尼比较困难,因此数值模拟方法就具有其明显优势。
Huse等[4-7]建立了锚泊阻尼计算的准静态模型,根据导缆孔处的水平运动幅值,建立了锚泊线在一个运动周期内最大竖向位移和锚泊阻尼的关系,计算中忽略了锚泊线在一个运动周期内最大水平位移的影响。Liu等[8]在Huse模型上进行了改进,认为锚泊线在平衡位置左右两侧的水平运动幅值并不对称,并在此基础上进行了改进,但是仍然忽略了锚泊线在一个运动周期内最大水平位移的影响。Bauduin等[9]又在Liu模型的基础上进行了改进,将锚泊线在一个周期内的运动均匀分成N步,每一步仍然假定是准静态的,得到了更符合锚泊线实际运动状况的计算公式。Raaijmakers等[10]和Papazoglou等[11]针对Huse模型进行了试验验证,认为准静态的计算方法具备一定的可行性。
Webster[1]利用时域有限元方法对由水平和竖向运动引起的锚泊阻尼进行了计算,并基于量纲分析进行了参数分析。Bompais等[12]基于线性化的悬链线方程建立了一种由于锚泊线运动引起的慢漂阻尼计算方法。Larsen等[13]针对柔性立管的整体动力性能进行了数值计算和模型试验的比较分析。Witz等[14]在此研究基础上建立了柔性立管动力性能计算的Benchmark模型。Hamilton等[15]在频域范围内建立了一种快速有效计算深水条件下锚泊阻尼的方法。
本文基于能量耗散原理计算锚泊阻尼,并针对三种具有相似静恢复力刚度,但不同类型的锚泊系统:悬链式、张紧式和半张紧式,分别采用准静定计算方法和非线性动力有限元时域分析方法,对其锚泊阻尼贡献进行比较计算。
2 阻尼计算原理
考虑锚泊线在平面内运动,只考虑锚泊线顶端水平X方向运动引起的锚泊阻尼,在一个运动周期τ内锚泊线耗散的能量E可以表示为

阻尼可以等效为线性化的阻尼系数B,所以,某一时刻锚泊张力在X方向的分量Tx可以近似表示为

假定锚泊线顶端导缆孔处的运动时程和上部平台的运动时程相同,而平台在波浪作用下的运动响应 q(t)假定为正弦运动,即q=q0sin( ωt),其中q0为平台运动响应幅值。所以,一个运动周期τ内锚泊线耗散的能量E可以近似地表达为

因此,根据计算得到的一个运动周期τ内锚泊线耗散的能量E就可以得到等效线性化的阻尼系数:

其中:耗散的能量E可以通过积分一个周期内的顶端张力—位移曲线得到,需要利用到准静定方法或有限元动力方法的计算结果。
3 准静定方法
在本文中,采取了Bauduin等[9]提出的B&N模型来进行准静定计算锚泊阻尼。在计算中,考虑了以下假定条件:(1)忽略锚泊线上惯性力的作用,只计算拖曳力;(2)锚泊线形态在任意时刻均满足准静定的悬链线方程;(3)忽略海床和锚泊线之间的摩擦作用;(4)忽略锚泊线上的切向拖曳力作用而只计算其法向拖曳力;(5)锚泊线的法向拖曳力通过Morion公式计算;(6)锚泊线顶端导缆孔处的位移可以假定为正弦运动。
3.1 锚泊线顶端水平位移离散化
将锚泊线在一个运动周期τ,划分成Δt=τ/2N个时间步长,在每个时间步长内锚泊线均满足悬链线形态,共需要计算N+1个悬链线形态,如图1所示。考虑对称性,只需要计算半个运动周期,那么此时,锚泊线在半个运动周期内的各时间步为tn=nΔt,其中,n=0,…,N。
定义整体坐标系XYZ和局部曲线坐标系X2Y2Z2如图2-3所示。
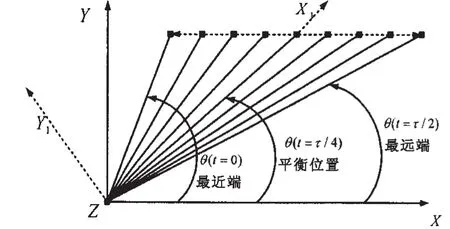
图1 锚泊线在一个激励周期内位置俯视图Fig.1 Top view of the mooring line positions during one surge oscillation
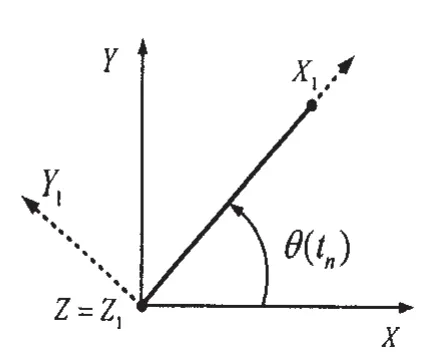
图2 锚泊线整体坐标系Fig.2 Mooring line global axes
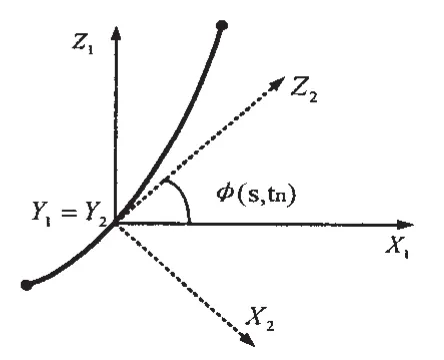
图3 锚泊线局部曲线坐标系Fig.3 Mooring line local axes
在每一个时间步tn下,导缆孔与锚固点之间的距离和方位角θ (tn)可以很容易得到,同时锚泊线形态也可以计算得到。锚泊线在tn-1和tn两个时间步之间的位移Δη( s,tn)如下:

其中:在tn时刻,锚泊线单元d s在局部坐标系中的坐标为(s,tn),而将其转化到整体坐标系中,则用X(,Y, )Z (s,tn)来表示。
此时,锚泊线单元 d s的法向位移分量 Δ ηn(s,tn)如下:
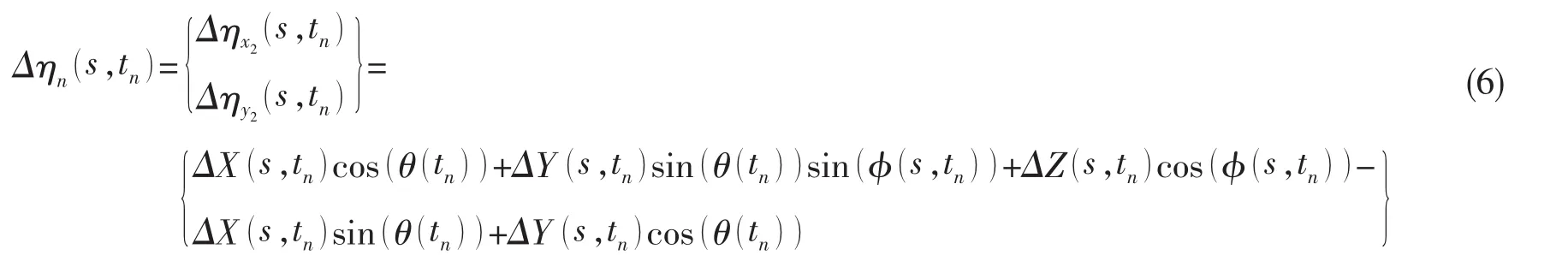
那么,锚泊线单元从最近端运动到最远端,即半个运动周期τ/2内的总法向位移ηn(s,tn)为:

根据对称性,可以得到另外半个运动周期τ/2内的总法向位移。
3.2 曲线拟合
由于锚泊线顶端激励位移为正弦运动,那么锚泊线单元ds的运动也应该是一个周期运动,可以利用傅里叶级数进行展开:

3.3 锚泊线耗散能量计算
通过对k=4截断后的(8)式进行微分,可以得到锚泊线的法向速度Vn(s,tn)。那么,就可以得到锚泊线单元ds所受到的拖曳力dF为:

4 非线性有限元动力方法
4.1 运动控制方程
在分析锚泊线的运动响应时,一般将锚泊线假定为完全挠性构件,其运动控制方程一般采用Berteaux[16]提出的


4.2 非线性有限元求解
根据(12)式可知,锚泊线的运动控制方程是一个复杂的时变强非线性方程,需要采用数值方法进行求解,本文采用非线性有限元法进行求解计算。采用单纯主从接触算法,假定海床为刚性海床平面,将锚泊线和海床分别划分为从面和主面,采用混合梁单元来模拟锚泊线,然后使用Newton-Raphson迭代法直接求解非线性问题[17]。
通过非线性有限元动力计算,可以得到锚泊线顶端位移工况下的张力时程曲线,然后通过计算张力时程曲线—顶端位移曲线的面积,即为锚泊线在一个激励周期内的耗散能量,利用(4)式就可以计算得到锚泊阻尼值。

图4 锚泊线静恢复力刚度Fig.4 Static offset curve of single mooring line
5 计算模型及参数
分别针对三种类型的锚泊线:悬链式、半张紧式和张紧式进行计算,锚泊线的布置如表1所示,锚泊线的材料属性如表2所示。三种类型的锚泊线具有相类似的静恢复力刚度,如图4所示。仅考虑静水条件下,比较锚泊线顶端水平运动时程分别为慢漂运动和波频运动对锚泊阻尼计算结果的影响,计算的各种工况如表3所示。
6 计算结果及分析
6.1 两种计算方法比较
为了比较准静定方法(QS)和非线性有限元时域分析方法(TD)在计算锚泊阻尼的区别和有效性,分别比较了锚泊线顶端施加慢漂激励幅值(q0)为50 m条件下的结果如图5(a)所示,波频激励幅值(q0)为5 m条件下的计算如图5(b)所示,其他工况下的结果详见表3。
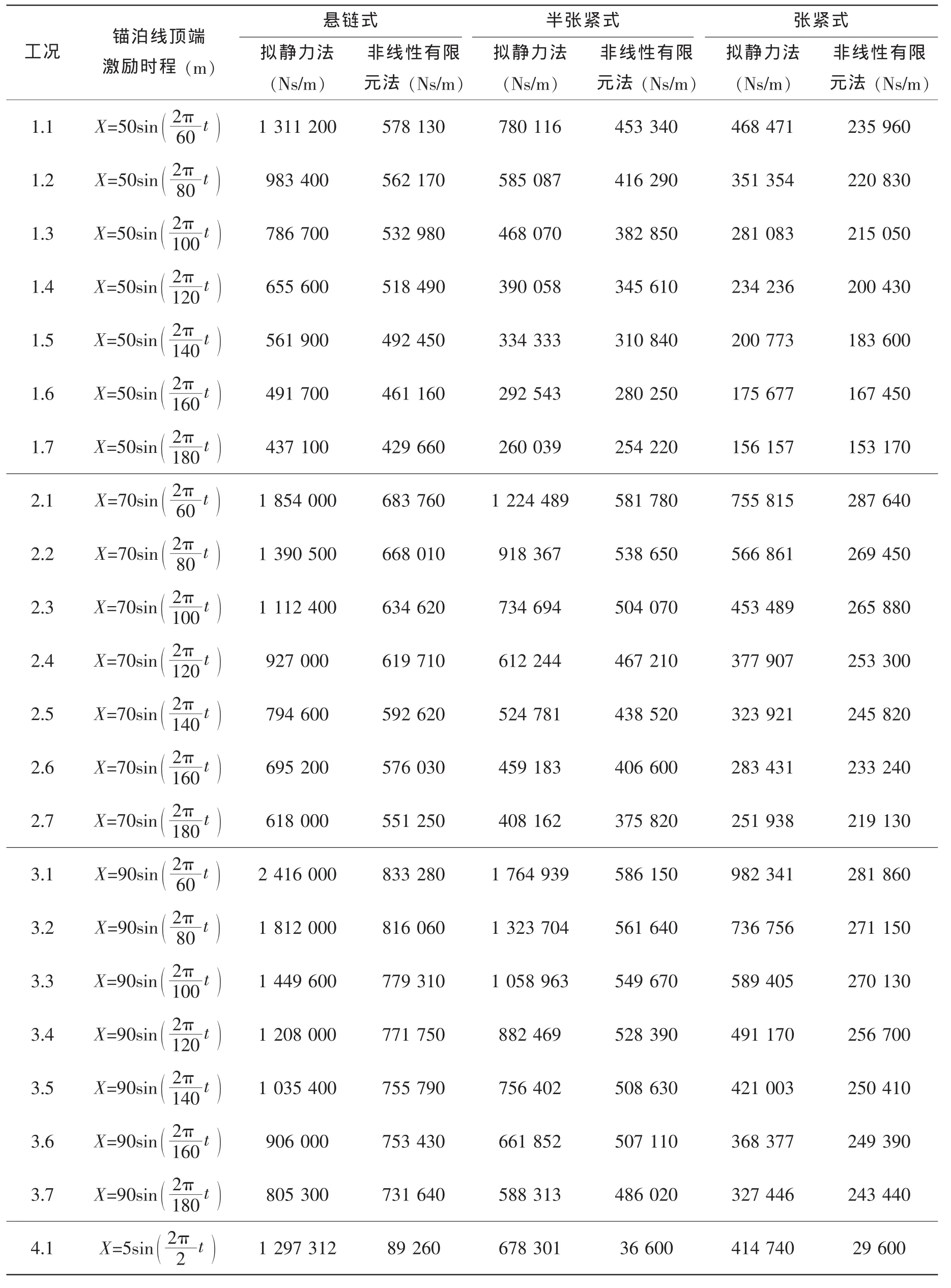
表3 锚泊阻尼计算参数及结果Tab.3 Calculation parameters and results of mooring damping

续表1
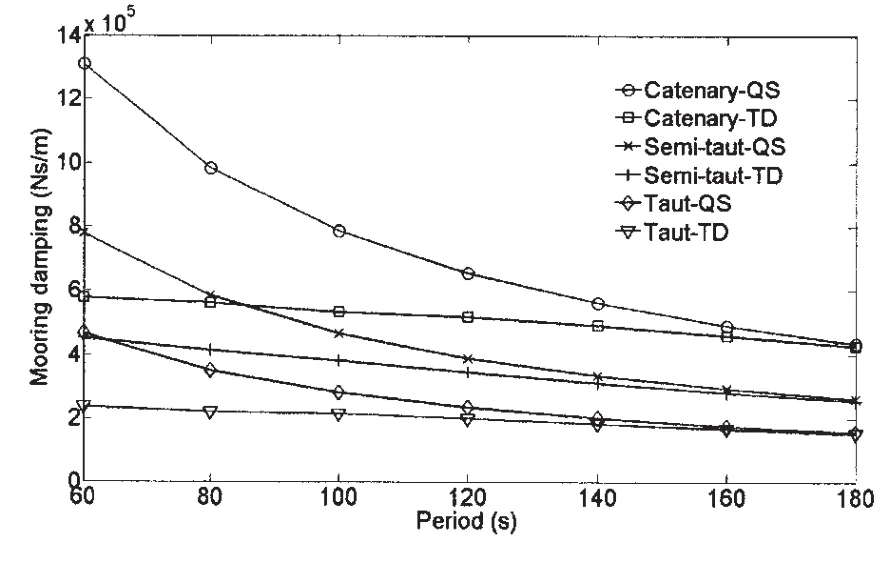
图5 (a) 慢漂激励下锚泊阻尼(q0=50 m)Fig.5(a)Mooring damping under low frequency excitation(q0=50 m)
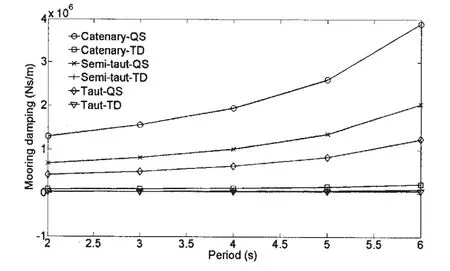
图5 (b) 波频激励下锚泊阻尼(q0=5 m)Fig.5(b)Mooring damping under wave frequency excitation(q0=5 m)
从图5可见,在慢漂激励下,随着慢漂激励周期的增加,拟静力方法和非线性有限元时域分析方法两者之间的计算结果越来越接近,当慢漂激励周期达到180 s时,两者的计算结果基本相同。换句话说,采用拟静力方法在计算锚泊阻尼时仅对长周期的慢漂激励计算结果比较准确。在波频激励下,随着波频激励周期的增加,拟静力方法和非线性有限元时域分析方法两者之间的计算结果始终相差很大,这表明利用拟静力方法计算波频激励下的锚泊阻尼是不准确的,容易产生很大的误差。
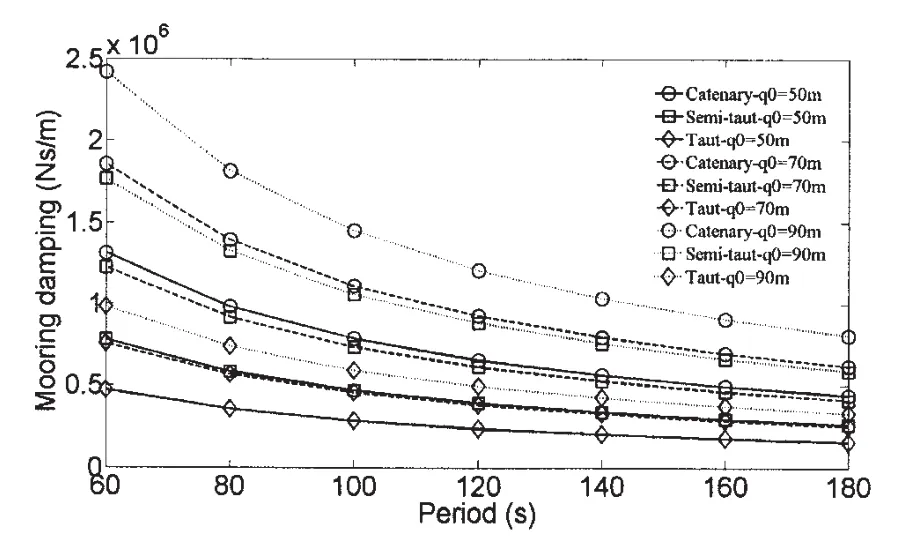
图6 不同锚泊方式阻尼(慢漂激励,拟静力方法)Fig.6 Mooring damping under different mooring layout(low frequency excitation,Quasi-static)
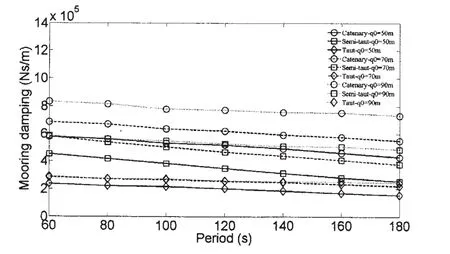
图7 不同锚泊方式阻尼(慢漂激励,时域方法)Fig.7 Mooring damping under different mooring layout(low frequency excitation,Time-domain)
6.2 不同锚泊方式对浮式平台的阻尼贡献比较
从图4可见,三种类型的锚泊系统具有基本相同的静恢复力刚度,他们之间的最大误差也在10%之内,然后比较不同的锚泊方式对浮式平台的阻尼贡献结果如图6-8所示,其中在低频激励下分别给出了利用拟静力方法和非线性有限元时域分析方法的计算结果,而在波频激励下仅给出时域计算方法的结果。
从图6-8可见,无论是在慢漂还是波频激励下,不同锚泊方式对浮式平台的阻尼贡献均为:悬链式>半张紧式>张紧式。随着慢漂激励幅值的增加,锚泊阻尼也增加。随着慢漂激励周期的增加,锚泊阻尼逐渐变小,而随着波频激励周期的增加,锚泊阻尼逐渐变大。
由此可见,即使具有相同的静恢复力刚度,不同锚泊方式对浮式平台的阻尼贡献差别仍然很大,在设计锚泊系统时,如何有效地利用锚泊阻尼,是需要进行详细思考的问题。
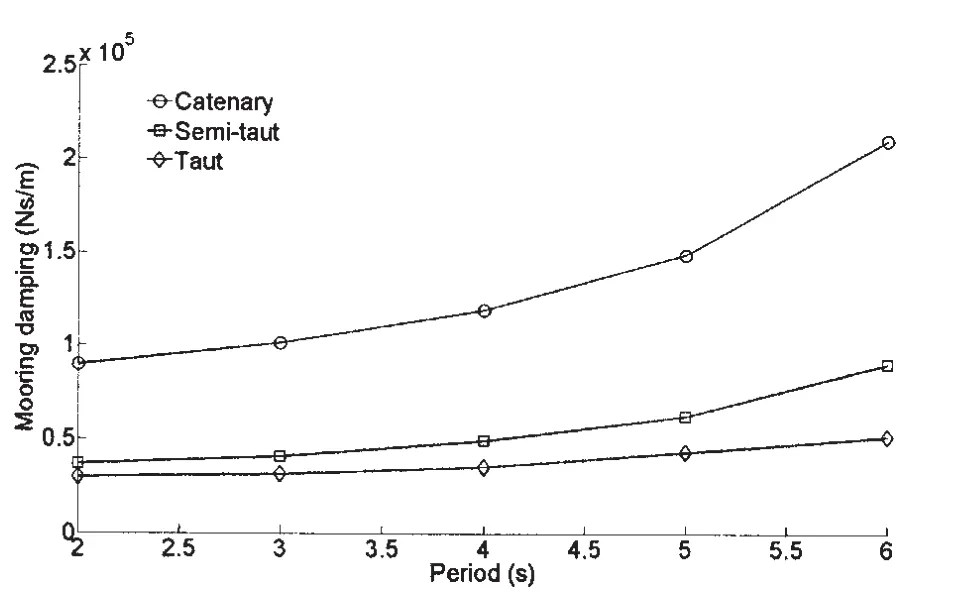
图8 不同锚泊方式阻尼(波频激励,q0=5 m)Fig.8 Mooring damping under different mooring layout(wave frequency excitation,q0=5 m)
7 结 论
分别利用拟静力方法和非线性有限元时域分析方法,针对悬链式、半张紧式和张紧式锚泊系统对浮式平台的阻尼贡献进行了比较计算,可以得到以下一些结论:
(1)采用准静定方法在计算锚泊阻尼时仅对长周期的慢漂激励计算结果比较准确,而利用准静定方法计算波频激励下的锚泊阻尼是不准确的,容易产生很大的误差。
(2)无论是在慢漂还是波频激励下,不同锚泊方式对浮式平台的阻尼贡献均为:悬链式>半张紧式>张紧式。随着慢漂激励幅值的增加,锚泊阻尼也增加。随着慢漂激励周期的增加,锚泊阻尼逐渐变小,而随着波频激励周期的增加,锚泊阻尼逐渐变大。
锚泊阻尼的有效计算方法是一个十分复杂的问题,如何针对不同工况,建立有效的估算方法,对于浮式平台的运动响应预测具有十分重要的意义。
[1]Webster W C.Mooring induced damping[J].Ocean Engineering,1995,22(6):571-591.
[2]Chen X,Zhang J,Ma W.On dynamic coupling effects between a spar and its mooring lines[J].Ocean Engineering,2001,28:863-887.
[3]Pinkster J A,Wichers J E W.The statistical properties of low-frequency motions of non-linearly moored tankers[C]//Offshore Technology Conference,May,1987.Houston,1987:OTC5457.
[4]Huse E.Influence of mooring line damping upon rig motions[C]//Offshore Technology Conference,May,1986.Houston,1986:OTC5204.
[5]Huse E,Matsumotk O.Practical estimation of mooring line damping[C]//Offshore Technology Conference,May,1988.Houston,1988:OTC5676.
[6]Huse E,Matsumoto K.Mooring line damping due to first and second order vessel motion[C]//Offshore Technology Conference,May,1989.Houston,1989:OTC6137.
[7]Huse E.New Developments in prediction of mooring system damping[C]//Offshore Technology Conference,May,1991.Houston,1991:OTC6593.
[8]Liu Y,Bergdahl L.Improvement on Huse’s model for estimating mooring cable induced damping[C]//Proceedings of the 17th International Conference on Ocean,Offshore and Arctic Engineering,July,1998.Lisbon,Portugal,1998.
[9]Bauduin C,Naciri M.A contribution on quasi-static mooring line damping[J].Journal of Offshore Mechanics and Arctic Engineering,2000,122:125-133.
[10]Raaijmakers R M,Battjes J A.An experimental verification of Huse’s model on the calculation of mooring line damping[C].Proceeding of the 8th BOSS Conference,1997,2:439-452.
[11]Papazoglou V J,Mavrakos S A,Triantafyllou M S.Non-linear cable response and model testing in water[J].Journal of Sound and Vibration,1990,140(1):103-115.
[12]Bompais X,Boulluec M L,Dekindt F,Marin S,Molin B.Slow-Drift Motion:Practical estimation of mooring line damping[C]//Proceedings of the 13th International Conference on Ocean,Offshore and Arctic Engineering.Houston,Texas,1994.
[13]Larsen C M.Flexible riser analysis comparison of results from computer programs[J].Marine Structure,1992,5:103-119.
[14]Witz J A.A case study in the cross-section analysis of flexible risers[J].Marine Structure,1996,9:885-904.
[15]Hamilton J,Kitney N.An alternative mooring line damping methodology for deep water[C]//Proceedings of the 14th International Offshore and Polar Engineering Conference,May,2004.Toulon,France,2004.
[16]Berteaux H O.Buoy Engineering[M].New York:Wiley Interscience Publication,1976.
[17]乔东生,欧进萍.深水悬链锚泊线阻尼计算[J].振动与冲击,2011,30(2):24-31.
Comparative calculation on damping contribution of different mooring types to deepwater floating platform
QIAO Dong-sheng1,FAN Tian-hui2,OU Jin-ping1,2
(1 Deepwater Engineering Research Center,Dalian University of Technology,Dalian 116024,China;2 State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)
Mooring damping provides important contribution to the motion response of deepwater floating platform.The dissipated energy by a mooring line from the floating platform as a result of its oscillation is applied to calculate the mooring-induced damping.The quasi-static method and nonlinear dynamic finite element in time domain method are introduced,respectively.Three types of mooring systems,which are catenary,semi-taut,and taut,have the similar static restoring force characteristics.The calculations on damping contribution of the three mooring types are compared.The results give the scope application of different calculation methods on mooring damping,and summarize the damping contribution of different mooring types.
mooring types;damping contribution;quasi-static;time domain analysis
P751 TV312
A
10.3969/j.issn.1007-7294.2014.05.004
1007-7294(2014)05-0507-09
2013-10-22
国家重点基础研究发展计划项目(973项目,No.2011CB013702;2011CB013703);国家自然科学基金项目(No.51209037;51221961);中国博士后科学基金特别资助项目(No.2013T60287)
乔东生(1983-),男,博士,大连理工大学讲师,E-mail:qds903@163.com;
樊天惠(1987-),男,大连理工大学博士生。

