双桨式吊舱推进器水动力性能CFD预报方法研究

马 骋 ，钱正芳 ，2，陈 科 ，蔡昊鹏 ，庄光宇

（1海军装备研究院，北京 100161；2海军工程大学，武汉 430033）

双桨式吊舱推进器水动力性能CFD预报方法研究

马 骋1，钱正芳1，2，陈 科1，蔡昊鹏1，庄光宇1

（1海军装备研究院，北京 100161；2海军工程大学，武汉 430033）

基于粘性流体CFD理论，数值预报双桨式吊舱推进器在均流和非均流条件下的水动力性能。均流条件下，采用多参考系模型和滑移网格模型，分别数值模拟前桨和后桨的旋转，将数值结果和试验结果进行了比较，推力的误差不大于4.51%，扭矩误差不大于3.35%；非均流条件下，在FLUENT软件中，以Profile的形式导入伴流数据文件，通过数值预报的平均值与敞水工况的试验结果做间接的比较，可以看到总推力系数偏差为5.26%，扭矩系数偏差为3.12%。结果表明，该数值方法对于双桨式吊舱推进器在均流和非均流条件下的水动力性能的预报精度可满足要求。

双桨式；吊舱推进器；CFD；水动力性能

1 引 言

吊舱推进器[1-3]作为一种新型的电力集成推进系统，已经越来越多地被应用于实船。吊舱推进器集成电机和螺旋桨于一体实现模块化设计，其在船舶上的布置也不再像传统螺旋桨那样受到轴系、主机的严格限制，可以布置在船首、船侧或者船尾等，目前其作为主推进器一般是吊挂在船尾下方，进流比传统螺旋桨要均匀，这在一定程度上有望改善其水动力、空泡、振动和噪声等性能。

在吊舱推进器研究领域，如何准确预报其水动力性能一直是研究的重点之一，因为这关系到吊舱推进器设计及性能的提高，也为工程实践提供重要的依据。双桨式吊舱推进器由于在吊舱包前后各布置一个螺旋桨，所以在双桨及吊舱包的相互影响下，其水动力性能也更为复杂。本文采用粘流CFD方法对双桨式吊舱推进器进行了在均流和非均流条件下的水动力性能预报，并与试验结果进行了比较分析，验证了该方法的可靠性。

2 CFD理论

2.1 雷诺平均N-S方程

在工程实际中，流动一般为湍流。而对于湍流的描述，从工程应用角度来看，重要的是湍流所引起的平均流场的变化，是整体的效果。由于在湍流流动中，物理量可以分解成一个平均量与一个脉动量的和，因此在模拟湍流时就只计算平均量，脉动量的影响通过某种模型在时均化的方程中体现出来，该方法称作雷诺平均法，也称作RANS方法。相应的雷诺平均N-S方程为：

2.2 湍流模型

本文选取理论上发展较为完善的SST k-ω模型[5]（shear-stress-transport）来封闭RANS方程。SST k-ω两方程湍流模型如下：

在这里，σk和σω分别是关于k和ω的湍流普朗特数。湍流粘度定义如下：

其中Gk同标准k-ω模型中所定义的湍动能产生项相同。ω的产生项定义为：

以上各式中，F1和F2均为混合函数；各经验系数定义及取值可参考文献[5]。

2.3 数值计算方法

2.3.1 多参考系模型方法

多参考系模型（Multiple Reference Frame（MRF）model）是一种常用的存在相对运动时的定常计算模型，特别是运动区域与静止区域间的相互作用比较微弱时。MRF模型的另外一个用途就是用来为非定常计算提供初始流场。在MRF方法中，计算区域划分为多个子域，每个子域的控制方程是针对子域参考系而写的。在两子域间的边界，子域控制方程的扩散项以及其他项需要邻近子域的速度值。使用相对速度公式，对每个子域的速度相对于子域的运动进行计算。从而使得速度和速度梯度从移动参考系转换到绝对惯性参考系。

2.3.2 滑移网格模型方法

滑移网格模型（Sliding Mesh model）假定流场是非定常的，因此数值模拟更精确地反应流场中旋转物体间的相互作用，从而保证了数值模拟的精确度。滑移网格技术的基本原理是将计算模型划分成多个部分，每个部分网格有自己独立的网格形式和网格边界面。两部分之间边界面的组合称为交界面，交界面两侧网格相互滑动，两侧的网格结点不要求相互重合，通过计算两侧的通量，使其相等。为了计算交界面的通量，首先在每一个新的时间步确定出交界面两边交界区的重合面，通过网格重合面的通量由交界面两边交界区的重合面计算。

3 计算对象

本文所研究的双桨式吊舱推进器在上海交通大学空泡水筒中进行了均匀来流状态下的水动力性能试验，试验按ITTC推荐的程序进行，结果已进行了筒壁修正。表1为吊舱推进器前、后螺旋桨的主要几何参数。

表1 螺旋桨主要几何参数Tab.1 The main geometric parameters of propeller

图1为计算对象双桨式吊舱推进器模型在空泡水筒中试验的照片。图2为计算模型的表面网格及计算域纵剖面局部网格。图3为计算域网格的划分，将计算域一共划分为三个区域：包围前桨叶的圆柱体旋转域1、包围后桨叶的圆柱体旋转域2以及一个静止的计算域3。在两个旋转域，域1、域2内划分网格时进行局部加密，以保证近壁面网格Y+值的取值范围（11.63＜Y+＜500）[6-7]，提高计算结果的准确度；域3为吊舱推进器所在的控制域，采用结构化网格，从而达到合理的减少计算网格的目的。

图1 模型试验Fig.1 Test model

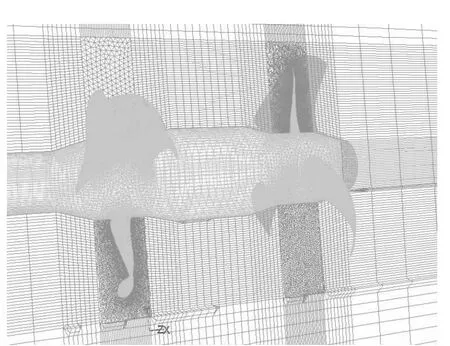
图2 计算模型Fig.2 Calculation model

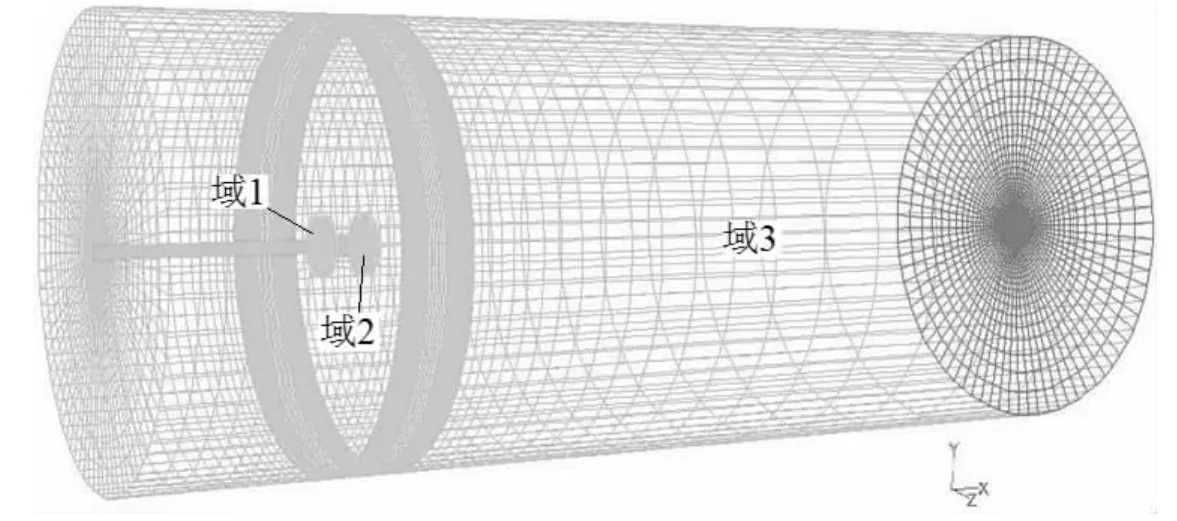
图3 计算域网格划分Fig.3 The computational domain mesh

4 均匀流条件下的水动力性能计算

4.1 边界条件的设置

入口设置为来流速度入口，出口定义为压力出口，物面为无滑移表面。特别地，在模拟双桨吊舱推进器各部件相互干扰情况时，考虑到后桨在前桨的尾流中运转，受前桨的影响很大，而同时后桨旋转产生的诱导速度场也会对前桨的性能有所影响。因此这里没有仅仅使用数值预报单桨定常水动力性能中经常使用的多参考系方法，而是使用了多参考系和滑移网格相结合的方法[8]，即前桨采用多参考系方法，后桨采用滑移网格方法。基于压力变量的SIMPLE耦合求解器，采用二阶迎风差分离散格式，结合低雷诺修正SST k-ω两方程湍流模型进行数值模拟。一般迭代计算2 000步就可以收敛。

4.2 计算结果分析

采用上述数值方法，对双桨式吊舱推进器水动力性能进行了预报，螺旋桨的推力系数KT、转矩系数10KQ以及敞水效率η计算结果（N=1 372 rpm）见表2，与试验值的比较如图4所示。从计算结果来看，对于双桨式吊舱推进器的推力系数KT、转矩系数10KQ的预报都较为准确，推力的误差不大于4.51%，扭矩误差不大于3.35%。

表2 计算值和试验值比较Tab.2 Comparison between the calculated results and test results

续表2

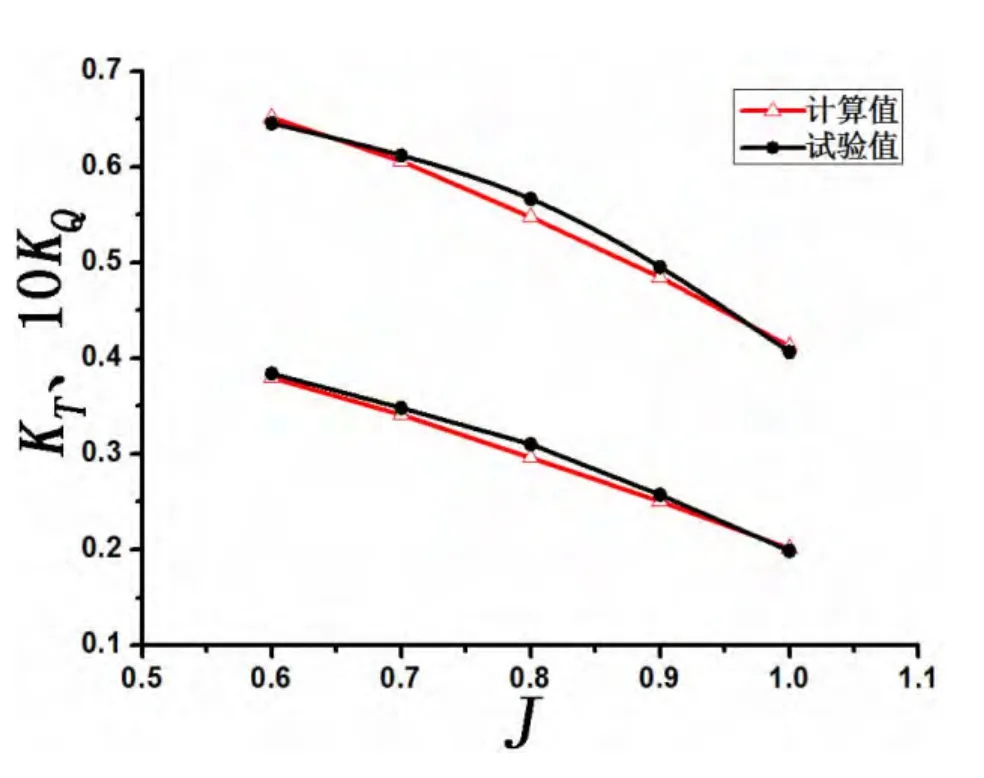
图4 敞水性能计算结果与试验结果比较Fig.4 Comparison between the calculated results and test results of the open water performance

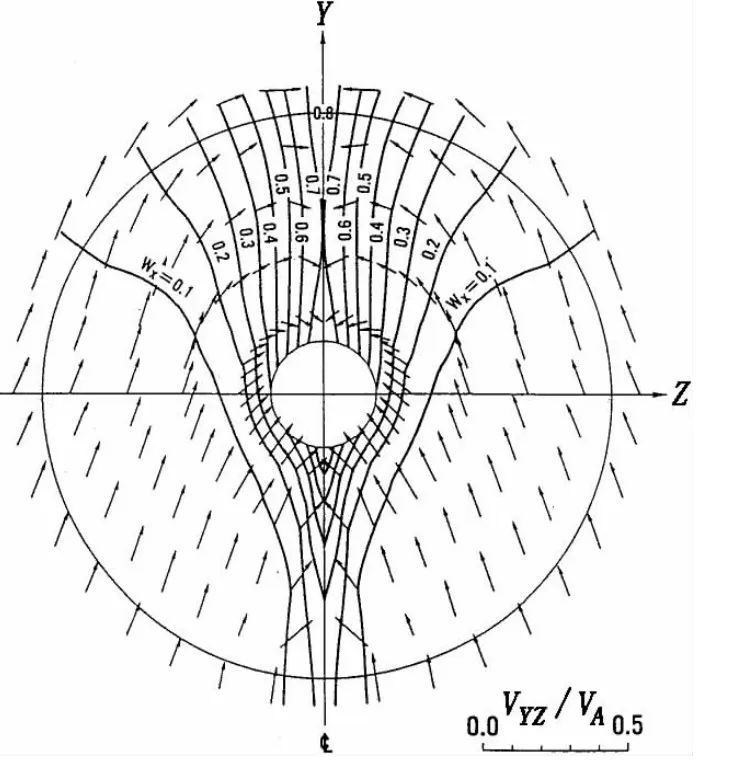
图5 伴流分布Fig.5 Wake distribution

5 非均流条件下的水动力性能计算

5.1 伴流分布的给定

本文为了使非定常特性更为明显，便于验证，选取某一散货船的船后伴流场为给定计算的流场，其分布[9]由图5给出，而真实的吊舱流场品质要比船后的好很多。在FLUENT软件中，以Profile的形式导入伴流数据文件。数值计算取转速N=1 493 rpm，此时Vmean=3.602。计算中前、后桨均采用滑移网格方法。

5.2 计算结果分析

5.2.1 螺旋桨的非定常力分析

如图6至图9所示，双桨式吊舱推进器前后桨推力系数、扭矩系数，及总推力系数、总扭矩系数的时域和频域结果可以看出，螺旋桨（三叶桨）非定常力的叶频特征明显，且以一倍叶频为主。但对于推进器总推力系数，呈现出六倍轴频幅值最大的特点，且该幅值小于后桨的一倍叶频（三倍轴频）幅值，如图7所示，说明双桨式吊舱推进器在前后桨非定常力相互耦合影响下，总的非定常力可能减小，且主要特征频率为前后桨叶数总和的一倍叶频。如图10至图11所示，前（后）螺旋桨的侧向力、垂向力的非定常力的一倍叶频特征明显，且前桨与后桨在时域上相邻峰值的角度差值与前后桨之间安装相位角度差相近。

从预报精度看，一个旋转周期内总推力系数KT-pro的平均值为0.262 2，螺旋桨总转矩系数10KQ-pro的平均值为0.469 2，与对应工况J=0.688 5时，推进器敞水推力系数的试验值为0.249 1，转矩系数试验值为0.455 0进行比较，总推力系数偏差为5.26%，扭矩系数偏差为3.12%。因此，非均匀伴流情况下双桨式吊舱推进器非定常水动力预报精度可满足要求。

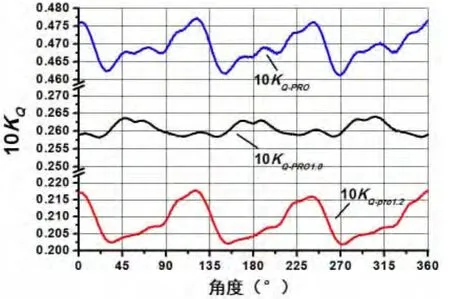
图8 螺旋桨扭矩系数Fig.8 Propeller torque coefficient

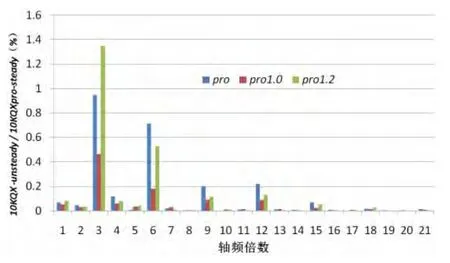
图9 螺旋桨扭矩系数轴频倍频程分析Fig.9 Analysis of axis frequency octave of propeller torque coefficient

图10 螺旋桨侧向力系数Fig.10 The lateral force coefficient of the propeller

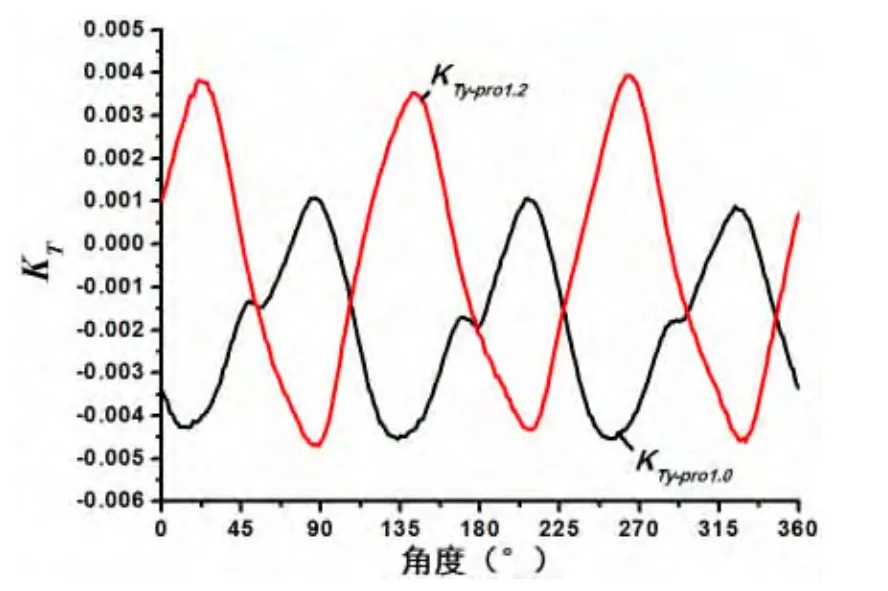
图11 螺旋桨垂向力系数Fig.11 The vertical force coefficient of the propeller

5.2.2 支架的非定常受力分析

支架在推进器运转过程中，也受到螺旋桨非定常力的作用，由图12至图15可知，双桨式吊舱推进器支架受到的轴向力、侧向力和垂向力的非定常力的成分均以三叶螺旋桨的一倍叶频为主。支架轴向力系数KTx-str的数值为负，说明在吊舱推进器工作时支架提供阻力；支架侧向力系数KTz-str与螺旋桨侧向力系数KTz-pro1.0和KTz-pro1.2处于同一数值量级上，表明支架侧向力与螺旋桨侧向力相关性较强，且支架侧向力对推进器操纵性也有较大影响，需在设计中关注；支架垂向力系数KTy-str的数值为负，且脉动幅值最小。

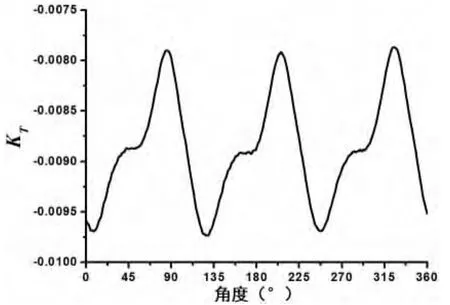
图12 支架轴向力系数KTx-strFig.12 The axial force coefficient of strut(KTx-str)

图13 支架的侧向力系数KTz-strFig.13 The lateral force coefficient of strut(KTz-str)

图14 支架的垂向力系数KTy-strFig.14 The vertical force coefficient of strut(KTy-str)

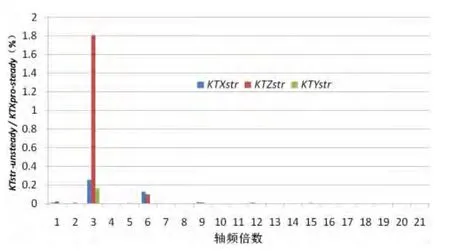
图15 支架各受力系数的轴频倍频程分析Fig.15 Analysis of axis frequency octave of three directional force coefficient of strut

图16 舱体轴向力系数KTx-podFig.16 The axial force coefficient of pod(KTx-pod)

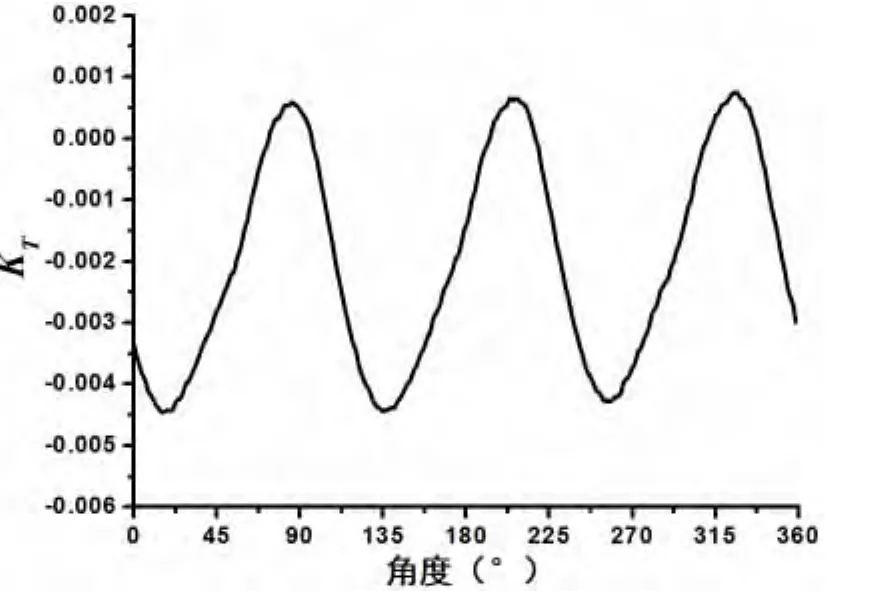
图17 舱体的侧向力系数KTz-podFig.17 The lateral force coefficient of pod(KTz-pod)

5.2.3 舱体的非定常受力分析

舱体在推进器运转过程中，也受到螺旋桨非定常力的作用，由图16至图19可知，双桨式吊舱推进器舱体受到的轴向力、侧向力和垂向力的非定常力的成分均以三叶螺旋桨的一倍叶频为主。舱体轴向力系数KTx-pod数值为负，说明在吊舱推进器工作时舱体提供阻力，量级和支架轴向力系数相当，两者之和约占螺旋桨总轴向力系数的6%，不能忽略；舱体侧向力系数KTz-pod与垂向力系数KTy-pod处于同一数值量级上，且与支架侧向力系数KTz-str相当，这些在吊舱推进器结构设计和操纵性研究中也需予以重视。

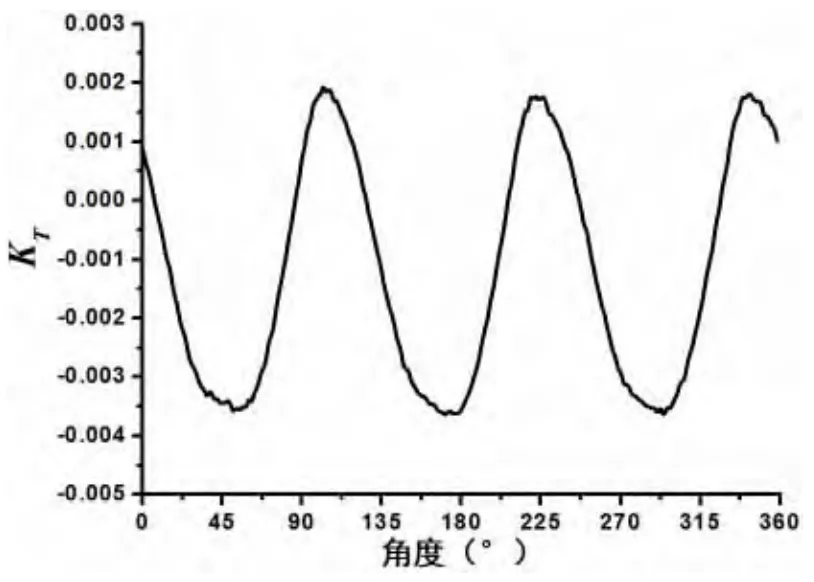
图18 舱体的垂向力系数KTy-podFig.18 The vertical force coefficient of pod(KTy-pod)

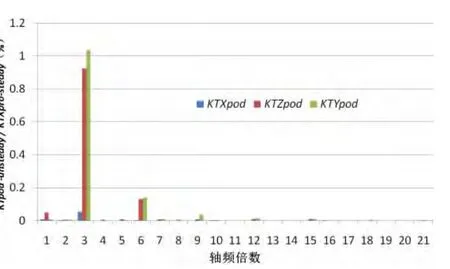
图19 舱体各受力系数的轴频倍频程分析Fig.19 Analysis of axis frequency octave of three directional force coefficient of pod

6 结 论

研究并建立了基于粘流理论，在均流条件下的双桨式吊舱推进器水动力性能的数值预报方法。通过将数值计算结果与实验结果进行了比较、分析，在设计工况J=0.9附近，推力系数的误差为2.68%，扭矩系数的误差为2.14%，验证了该数值求解方法对于双桨式吊舱推进器在均流条件下的水动力性能的数值预报是准确的、可行的。

研究并建立了基于粘流理论，在非均匀来流条件下的双桨式吊舱推进器水动力性能的数值预报方法。通过数值计算、结果比较和特性分析，在设计工况附近，螺旋桨轴向力系数的平均值与试验值相差5.26%，扭矩系数的平均值与实验值相差3.12%，证明了该方法能够有效预报双桨式吊舱推进器在非均匀来流条件下的水动力性能，双桨式吊舱推进器的前桨、后桨、舱体、支架等部件非定常力的成分以一倍叶频为主。

[1]马 骋,钱正芳,张 旭.POD推进器性能和军事应用研究[C]//第十七届全国水动力学研讨会暨第六届全国水动力学学术会议文集.香港,2003.

[2]马 骋.吊舱推进技术[M].上海:上海交通大学出版社,2007.

[3]马 骋.舰船吊舱推进器水动力学[M].北京:国防工业出版社,2009.

[4]王福军.计算流体动力学分析—CFD软件原理与应用[M].北京:清华大学出版社,2004.

[5]ANSYS,Inc.,ANSYS FLUENT 12.0 Theory Guide[K].ANSYS,Inc.,2009.

[6]Fluent Inc.,FLUENT User’s Guide[K].Fluent Inc.,2003.

[7]Versteeg H K,Malalasekera W.An introduction to computational fluid dynamics:The finite volume method[M].Wiley,New York,1995.

[8]庄光宇,蔡昊鹏,马 骋等.双桨式吊舱推进器水动力性能CFD预报建模方法研究[C]//第二十五届全国水动力学研讨会暨第十二届全国水动力学学术会议文集.浙江舟山,2013.

[9]苏玉民,黄 胜.船舶螺旋桨理论[M].哈尔滨:哈尔滨工程大学出版社,2003.

Research on the CFD prediction method of hydrodynamic performance of tandem type podded propulsor

MA Cheng1,QIAN Zheng-fang1,2,CHEN Ke1,CAI Hao-peng1,ZHUANG Guang-yu1
(1 Naval Academy of Armament,Beijing 100161,China；2 Naval Univ.of Engineering,Wuhan 430033,China)

A numerical method based on CFD theory is proposed for predicting the steady and unsteady hydrodynamic performance of tandem type podded propulsor.For the steady hydrodynamic performance,the maximum error of thrust is 4.51%,the maximum error of torque is 3.35%;For the unsteady hydrodynamic performance,the error of thrust is 5.26%,the error of torque is 3.12%.The result shows that the numerical method presented in this paper has good precision in the prediction of steady and unsteady hydrodynamic performance of tandem type podded propulsor.

tandem type;podded propulsor;CFD;hydrodynamic performance

U661.313

A

10.3969/j.issn.1007-7294.2014.05.005

1007-7294（2014）05-0516-08

2014-02-17

马 骋（1963-），男，海军装备研究院研究员；

钱正芳（1973-），男，海军装备研究院高级工程师；

陈 科（1980-），男，海军装备研究院工程师，E-mail：ck3008409@163.com。