雨流计数法误差详析方法的提出及实例研究

陈 晶，金永兴，肖英杰，毛奇凰，吴华锋

（上海海事大学 商船学院，上海 201306）

雨流计数法误差详析方法的提出及实例研究

陈 晶，金永兴，肖英杰，毛奇凰，吴华锋

（上海海事大学 商船学院，上海 201306）

文章依据频谱分析以及应变能量原理，对雨流计数法的系统误差进行定量分析。并结合集装箱船的现场采样数据，提供给业界一种定量计算雨流计数法误差的方法，可在进行结构疲劳计算时，根据应力曲线的定量特征和工程精度要求，来确定是否适合选用雨流计数法进行计算。

位错；雨流计数法；应变能；载荷频谱

1 引 言

金属构件的疲劳，源自金属结构内局部范围反复形变产生的塑性应变。这些结构在使用中所出现的应力历程十分复杂，主要是由于交变载荷产生的应变能，造成与加剧受力点在微观结构上的位错。位错反复累积，一定程度之后，越发呈现宏观裂纹。裂纹继续扩展，最终导致结构失效。实测可知，这种结构的应力时间历程符合随机宽带过程，可采用循环计数法，统计出全部历程中各种幅值的应力循环次数。在各种计数法中，雨流计数法的原理与材料疲劳损伤机理吻合较好，在业界被视作复杂载荷历

程中损伤计算的首选方法。雨流计数法又可称为塔顶法，最早由英国的Matsuiski和Endo两位工程师提出，在疲劳寿命计算中运用非常广泛[1-4]。算法的操作过程，是把“载荷—时间”历程数据记录转过90°，时间坐标轴竖直向下，数据记录犹如一系列屋顶檐面，应力往复幅值与次数的统计过程类似于雨水顺其而下的画面，故称为雨流计数法。

雨流计数法的优势在于：该方法对载荷的时间历程进行计数的过程反映了材料的记忆特性，具有明确的力学概念，与结构疲劳理论较为契合；同时算法流程简便，广泛适用于工程领域的疲劳计算。但该法在精度上存在显著局限：应力采样历程曲线在计数之前，须做简化（锯齿化）预处理。预处理过程将采样曲线简化为折线段，舍弃复杂的折曲细节。如果不做预处理，则无法确保计数过程正常进行。尤其对于能量谱分布较宽的海浪载荷，简化处理将丢失掉诸多不应忽视的应变能量，导致某些场合计算误差显著。

关于雨流计数法在精度等方面的局限，文献[1-5]等有定性阐释，其中文献[3]、[5]在定性阐释后，对其进行了一定程度的改进，但依然无法回避简化预处理过程中造成的系统误差。至于简化预处理过程中造成误差的信号学原理，学界及工程界目前几乎没有进行过系统的定量分析。就此，本文展开两部分工作：

（1）依据频谱分析以及应变能量原理，对雨流计数法的误差进行误差的定量分析[6]；

（2）结合实体集装箱船采样数据，得到精确的定量分析结果以及雨流计数法的实际工程误差情况，以此例提供给业界一种定量的计数法误差分析方法，可在进行结构疲劳计算时，根据应力曲线的定量特征和工程精度要求，来确定是否适合选用雨流计数法进行计算。

2 雨流计数法误差详析方法的提出

基于傅里叶频谱分析以及应变能量原理，对不同应力载荷在离散采样过程中形成的误差，提出一套理论相对较完备的误差详析方法。

实际工程中的各类载荷采样曲线均为离散时间序列采样。对于较高精度的采样序列，可以较为准确地反映载荷曲线的基波波形以及各阶谐波。而雨流计数法将忽略掉任意相邻两极值点间的所有中间采样点。如图1所示，设X（ k- 1 ）与X（k）是某相邻两极值点，两点间的实际载荷曲线有诸多可能。图1中左图为单一拐点、驻点（凸性改变）情况的曲线簇，右图为无拐点、驻点（凸性不变）情况的曲线簇，另外还有存在多个拐点、驻点（凸性多次改变）的特殊情况。

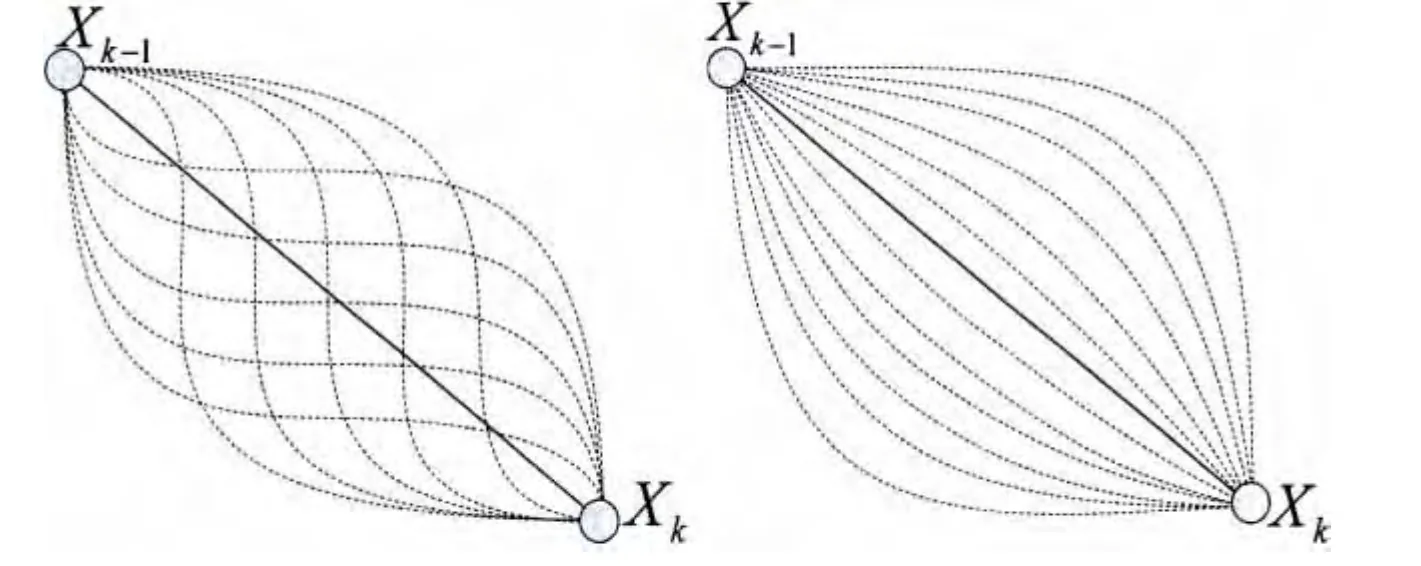
图1 采样历程中两极值点间应力变化曲线的各类可能情况（左图为有拐点、驻点情况，右图为无拐点、驻点情况）Fig.1 Various possible stress curves between two extreme points in the sampling history(Left:situation with Inflection and Stagnation points,Right:situation with no Inflection and Stagnation points)

而动载荷疲劳理论研究存在两处关键：（1）动载荷的变化范围与变化中心（动载荷的期望值）；（2）动载荷变化速率的分布情况（以dσ/dt表示）。以上两个因素对结构体局部位错严重程度都将产生直接影响。鉴于以上考察指标，图1所示的两点之间，不同类型的曲线将导致动载荷的期望值以及变化速率dσ/dt的时序分布发生差异很大，所对应的结构疲劳损耗也各不相同。两相邻极值点间隔时间越大，不同类型载荷曲线对结构体影响的差异也越大。但依据计数法要求，中间若干非极值点均被忽略掉，换以直线代替，不同的载荷曲线均简化为同一条直线段，从而得到完全相同的应力集中点疲劳损耗数值，势必引起不可忽略的计算误差。在各种极端曲线情况下，误差在结果数值中的占比将高到无法忽视的程度。

为了便于更加直接、量化地呈现曲线简化处理后的误差情况，基于对图1的分析，下面采取由图1中两点之间四种有代表性的曲线形式组成的四组不同的曲线序列为例（如图1所示），分析计数法在原理上存在的误差。为使分析过程简洁清晰，四组波形有统一的设定：（1）载荷作用点结构类型相同，疲劳损耗过程满足W型S-N疲劳曲线[8]；（2）载荷范围相同，均为25-85 N/mm2；（3）载荷波形为严格周期函数，周期T均为3S，采样时间均为4个完整周期；（4）计算与绘制载荷频谱时，傅氏变换的时域窗口宽度均为3S，与载荷周期一致，以使傅氏载荷谱无能量泄漏的问题；（5）波形图中点划线为交变载荷的期望值，虚线为雨流计数法的简化历程。

四组波形图如图2所示。

图2 四类交变载荷序列Fig.2 Four types of alternating load sequence

（a）简谐震荡（正弦）式交变载荷

简谐震荡式交变载荷是最常用于应力测试的交变载荷形式，也是最贴近船舶行驶中受海浪施加于船体的交变载荷形式（实际海浪波形可拆解为一系列两两正交的简谐震荡波）。本文中曲线具体采用表达式 30·sin（ 2πx/3+ ）θ，波形如图 2（a）所示。

该交变载荷的特点是：载荷的期望值线为载荷数值分布的几何中心，交变能量围绕期望值呈现对称分布，载荷的交变速率亦遵从正弦交变规律，即载荷的交变不但存在一定的速率，还存在加速度（且加速度亦随时间交变），即载荷对受力对象的施加方式在不断地改变，对受力对象微观结构的影响是最不容忽视的。

该载荷历程的傅氏载荷谱如图3（a）所示。该载荷频谱图像定量显示了简谐波式交变载荷的应变能密集程度，几乎全部能量都集中在基频（1倍频）处（实际操作中由于数值计算的误差，有极少能量散落在其他频段）。应变能的集中性使同等能量下载荷的交变幅度达到理论最大值（60 N/mm2）。应变能产生的致损功率经过定量计算得到为8 879 kW（参数k=Aσ2l·ΔT/2ET，其中E为杨氏模量，ΔT为采样周期，T为波形周期，A为受力面积，σ为交变应力幅值，l为受力体静载时尺寸）。

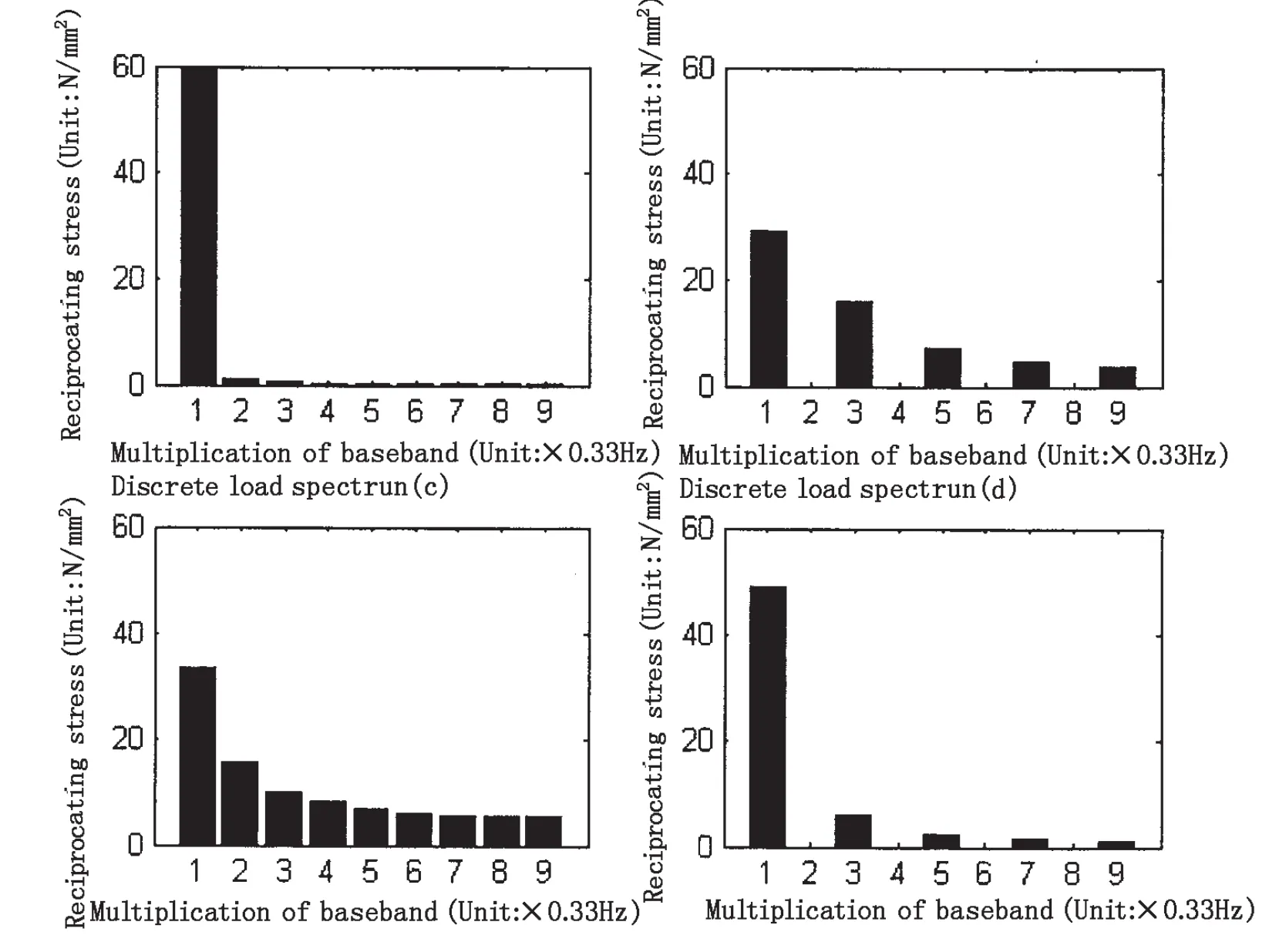
图3 四类交变载荷频谱图Fig.3 Four types of alternating load spectrogram

依据S-N曲线中W型应力集中点受力公式，得到该段载荷序列对该受力点造成的积损程度为千万分之23.69，即该受力点在结构失效前总共可承受此交变载荷约1 407小时（具体计算公式详见《船体结构疲劳强度指南》[8]）。

（b）双边尖脉冲式交变载荷

此类交变载荷在实际工况中也时有出现。 本文曲线由表达式±60·［4（ x - θ ）/3 ］3组合而成，波形如图2（b）所示。与简谐震荡类似的是，载荷的期望值线为载荷数值分布的几何中心，交变能量围绕期望值呈现对称分布。但该交变载荷也存在独特的规律：载荷数值在多数时间相对平稳，并按一定频次在两个方向交替出现近似的尖脉冲；交变速率dS/dt以及加速度在多数时间相对较小，同时也按一定频次出现脉冲式变化；交变载荷在交变范围上下限附近停留时间很短。

该载荷历程的傅氏载荷谱如图3（b）所示。由于该类载荷波形与正弦波形存在差异，在做波形的傅氏正交变换后，可知载荷的能量并非集中在一个频段，而是明显地散落到奇数倍频段里，能量相对集中的基频的载荷交变幅值仅为29 N/mm2，应变能经过定量计算为2 926 kW，显著低于简谐震荡式载荷。

由于S-N曲线的对数线性关系，这种影响的差异又会显著放大，即受力点可承受该类载荷的交变总次数将远远超过上一种形式的两倍。通过定量计算，得到该段载荷序列对该受力点造成的疲劳积损程度为千万分之2.75，即该受力点在结构失效前总共可承受此交变载荷约12 121小时。

（c）单边尖脉冲式交变载荷

单边尖脉冲式交变载荷是另一种常见的脉冲式载荷。本文中曲线具体由半圆表达式20·（9-（tθ ）2）1/2组合而成，波形如图2（c）所示。与前两者显著不同的是，载荷序列的交变情况呈现非对称分布，不存在几何中心，期望值线靠近曲线较平缓的一端，交变能量也随之呈现非对称分布。载荷数值在多数时间相对平稳，并按一定频次在某个方向出现近似的尖脉冲；交变速率dS/dt以及加速度在多数时间相对较小，同时也按一定频次出现脉冲式变化，在载荷交变幅度相同的前提下，交变速率与加速度的变化幅度显著高于双边脉冲；交变载荷在交变范围极限附近停留时间很短。

该载荷历程的傅氏载荷谱如图3（c）所示，此类载荷的能量亦十分分散。能量相对集中的基频的载荷交变幅度为34 N/mm2，略高于双边脉冲形式。应变能的致损功率经计算为2 362 kW，同时该段载荷序列对该受力点造成的疲劳积损程度为千万分之4.20，即该受力点在结构失效前总共可承受此交变载荷约7 937小时。

（d）锯齿波式交变载荷

此类交变载荷正是雨流计数法对实际载荷曲线简化后的常见形式。本文中曲线具体采用表达式30·（±t- θ ）组合而成，波形如图2（b）所示。 载荷的交变数值分布对称，存在几何中心，期望值在几何中心，交变能量围绕期望值分布对称。交变速率dS/dt恒定（无交变加速度），交变载荷在交变范围上下限附近停留时间较短。

该载荷历程的傅氏载荷谱如图3（d）所示。此类载荷与简谐震荡式的几何差异较小，能量亦较集中。能量集中的基频的载荷交变幅度为49 N/mm2。应变能产生的致损功率经过定量计算得到为6 120 kW，同时该段载荷序列对该受力点造成的疲劳积损程度为千万分之12.71，即该受力点在结构失效前总共可承受此交变载荷约2 623小时。

如表1所示，四种典型的载荷形式，交变范围与周期均相同，而载荷交变速率、应变能、载荷期望值与载荷谱等情况差异显著，精确计算得出的单位时间的积损差异亦较大。但是依照雨流计数法，则将上述四类曲线统一简化为第四类，并通过计数得到与简谐震荡式载荷相同的积损结果。如果工况中的载荷采样接近第二类形式，计算结果的误差可能高达数倍。通过绘制频谱图及计算交变载荷的应变能，可得到使用雨流计数法而造成误差的具体数值。下节中以实际运行的集装箱船所受应力数据为例，探讨雨流计数法的可能存在的实际误差。

表1 四类交变载荷分析结果对比Tab.1 Analysis results and contradistinction of four types

图4 育锋轮应力载荷采样点布局Fig.4 The layout of the stress load sampling points of YU FENG

3 实船应力集中点采样分析

与陆上载运工具有所不同，船体结构承受的应力载荷周期和交变幅值都较大，应力采样系统有较大余力采入载荷波形的细节。以上特点使雨流计数法的精度局限十分凸显，适宜对其误差做定量分析。

本节以上海海事大学校船“育锋轮”实际航行中所测数据为例，以实验数据探讨雨流计数法的误差。采样点为“育锋轮”船舯左舷S6点，如图4所示。

抽取S6点在某夏季航次中的持续时长为30.6S、采样点为36个、采样周期为0.85S的一段载荷序列，如图所示。图中虚线部分即该点在航行中某时段所承受的应力载荷序列，而实线部分为雨流计数法进行简化处理后的序列。

图5 S6点载荷采样与载荷频谱图Fig.5 Sampling curve and spectrogram of load on S6

依照前节所述的详析方法，计算得到S6点的积损为千万分之31.30（傅氏载荷频谱经过相位及屏宽补偿）。采用雨流计数法将序列中的大小循环提取出来并算出每个循环单独对应的疲劳积损（详见表2），求和得到结果为千万分之35.51，误差值为千万分之4.21，计算误差率为+4.21/31.30=+13.45%。由此可见，由于计数法存在的系统误差，导致计算结果的偏差较为显著。

表2 实测数据计算结果对比Tab.2 Calculated results and contradistinction of real data

4 结 论

综上所述，可以得出雨流计数法计算过程中出现系统误差的原因主要有以下三点：

（1）相同交变范围的前提下，对应的应变能可能会有较大差异，不同大小的应变能导致结构体的位错程度各不相同，但经过雨流计数法的简化预处理后，应变能均相同，且等于锯齿波的应变能；

（2）载荷曲线经过简化处理，造成曲线基本形状在细节上的信息丢失。在相邻的两个极值点之间，曲线的形状均被简化为交变速率dσ/dt恒定的直线段，结构体所受到的交变冲击均简化为力度恒定而方向交变的冲击；

（3）曲线在简化后呈现锯齿波的形式，而统计交变载荷循环的积损时，实际是按照简谐震荡（正弦波）的情况统计。

由于上述计算过程存在多处理论性错位，雨流计数法的系统误差在多个环节相叠加，有些工况下可能相互抵消，但也可能显著到难以忽略。本文主旨在于提供给业界一种定量计算雨流计数法误差的方法，可在进行结构疲劳计算时，根据应力曲线的定量特征和工程精度要求，来确定是否适合选用雨流计数法进行计算。在某个具体工况的实际工程计算中，使用雨流计数法之前，可先用部分采样点进行傅氏频谱分析与交变载荷的能量分析，并用雨流计数法进行比照实验，得到计数法在该工况下的误差率，当误差率满足工程计算要求时，即可方便地采用雨流计数法。

[1]金 丹,陈 旭.多轴随机载荷下的疲劳寿命估算方法[J].力学进展,2006,36(1):65-69.

[2]Bannantine J A,Socie D F.Multiracial fatigue life estimation techniques[M].In:Mitchell M,Langraf R,eds.Advances in Fatigue Lifetime Predictive Techniques.ASTM STP 1122.Philadelphia,American Society for Testing and Materials,1991:249-275.

[3]Anthes R J.Modified rainflow counting keeping the load Sequence[J].Int J Fatigue,1997,19:529-535.

[4]Langlais T E,Vogel J H,Chase T R.Multiaxial cycle counting for critical plane methods[J].Int J Fatigue,2003,25:641-647.

[5]田 军,李 强.改进的雨流法实时计数模型[J].北京交通大学学报,2009,33(1):29-31.

[6]杨咏漪,廖海黎,李永乐.大跨度桥梁风致抖振疲劳频域分析[J].空气动力学学报,2009,27(1):11-16.

[7]李珊珊,黄志博,崔维成.从短期测量数据来生成疲劳载荷的一种实用算法的开发[J].船舶力学,2011,15(3):286-300.Li Shanshan,Huang Zhibo,Cui Weicheng.On implementing a practical algorithm to generate fatigue loading history or spectrum from short time measurement[J].Journal of Ship Mechanics,2011,15(3):286-300.

[8]船体结构疲劳强度指南[M].上海:中国船级社上海规范研究所,2007:8-29.

A kind of error detailed analysis program proposed for rain-flow counting method and case study

CHEN Jing,JIN Yong-xing,XIAO Ying-jie,MAO Qi-huang,WU Hua-feng
(Merchant Marine Academy,Shanghai Maritime University,Shanghai 201306,China)

Based on the spectral analysis and the strain energy theory,the systematic errors of Rain-flow counting Method were quantitatively analyzed.Combined with sampling data of the real container ship,a quantitative method for calculating the systematic errors of Rain-flow counting Method is put forward to the engineering field,which may decide the selection of Rain-flow counting Method based on the quantitative characteristics of the stress curve and engineering accuracy requirements when calculating structural fatigue life.

Rain-flow Counting Method;strain energy;stress load spectrum;Fourier series

U661.4

A

10.3969/j.issn.1007-7294.2014.05.009

1007-7294（2014）05-0550-07

2013-08-16

中央高校基本科研业务费专项（10CX05005A）；国家自然科学基金资助项目（51279099）；上海市科学技术委员会基金资助项目（12ZR1412500）；上海市教委科研创新基金资助重点项目(13ZZ124)；上海市教育委员会和上海市教育发展基金会“曙光计划”基金资助项目（12SG40）；交通运输部应用基础研究项目（2013329810300）；上海海事大学优秀博士学位论文培育项目（2013bxlp004）

陈 晶（1982-），男，上海海事大学博士研究生，E-mail：chenjing_taixing@163.com；

金永兴（1959-），男，上海海事大学商船学院教授，博士生导师。