半潜式平台关键结构全寿期极限强度预报方法研究

嵇春艳，于雯，黄山，张健

（1江苏科技大学，江苏镇江212003；2英国斯特莱斯克莱德大学，英国格拉斯哥市）

半潜式平台关键结构全寿期极限强度预报方法研究

嵇春艳1，于雯1，黄山2，张健1

（1江苏科技大学，江苏镇江212003；2英国斯特莱斯克莱德大学，英国格拉斯哥市）

文章基于逐步破坏分析法和有限元计算方法，发展了一种计及材料腐蚀、疲劳裂纹等结构损伤的半潜式海洋平台关键结构全寿期极限强度计算方法。以一服役水深为3 000 m半潜式平台为研究对象，选取横撑和立柱局部结构作为研究对象，以不同服役年限下裂纹扩展长度和腐蚀厚度作为变化参数，采用ANSYS软件建立其参数化有限元模型，计算了不同服役年限下半潜式海洋平台关键结构极限强度，在此基础上分析了全寿期内关键结构极限强度随服役年限的变化规律。

半潜平台；关键构件；关键节点；极限承载力；疲劳裂纹；腐蚀

0 引言

我国自主建造的3 000 m半潜式平台属于第六代半潜式钻井平台，是当今世界上最先进的深水半潜式钻井平台类型。该海洋平台的主船体有两个上部箱体、四个立柱、四根横撑及两个下浮体组成，两个下浮体由位于立柱下部的四根横撑连接，上部箱体结构由四个立柱与下浮体相连，如图3所示。该平台主要服役我国南海海域，海况复杂，平台在服役过程中长期受到海水腐蚀和波浪荷载的作用，随着平台服役年限的增加，在环境荷载、结构腐蚀、疲劳裂纹的影响下，结构的抗力会降低，从而增加结构失效的风险，因此其全寿期的安全性评估显得尤其重要。

国内外很多学者对海洋结构物的极限强度分析已经作了很多研究，方法比较成熟。Petrusja等[1]应用非线性静力分析法分析了墨西哥湾一座平台的极限承载能力，从而推出了平台的失效概率。聂炳林[2]应用SESAM软件建立平台的模型，对平台进行了非线性倒塌分析。谢文会等[3]提出了半潜式钻井平台典型节点强度分析方法。上述的研究工作主要是针对设计状态结构进行的，不考虑结构在服役期内受到的腐蚀、裂纹、碰撞凹陷等机械性损伤。而随着平台服役时间的增加，平台结构尤其是平台结构的关键部位的全寿期极限强度问题备受关注。Paik，王生楠等[4-7]学者对考虑结构裂纹影响下板的极限强度做了大量的研究，对含裂纹板和加筋板结构剩余极限强度进行了评估。嵇春艳等[8]考虑腐蚀、裂纹的随机性，对固定式老龄化平台和半潜式平台极限强度及动态可靠性进行了研究。但上述的研究结果仍局限于简单的板或加筋板，或固定式平台结构，对于半潜式海洋平台复杂的节点结构、关键的横撑构件等如何考虑腐蚀、裂纹等结构损伤对其极限强度的影响仍有待深入研究。本文在半潜式平台整体强度分析的基础上，选取应力分布较大的立柱和横撑部分作为平台关键构件及关键节点模型，采用ANSYS有限元分析软件计算完整构件和节点的极限强度，开发了腐蚀和裂纹损伤模拟的局部程序计算模块，结合此计算模块建立以腐蚀厚度、裂纹尺寸等为变量的参数化有限元模型，通过弧长法获得半潜式平台关键节点和关键构件不同服役年限内的极限强度及变化趋势。

1 极限承载力计算方法[9]

半潜式平台是由加筋板组成的大型超静定结构，其达到极限状态时是一个复杂的非线性过程。计算非线性结构的系统响应，最常用的迭代方法是修正的牛顿-拉普森迭代法和弧长法，本文使用弧长法进行极限强度求解。弧长法使得牛顿—拉普森法平衡迭代沿一段弧收敛（图1）。弧长法中每一载荷步由外载荷增量和平衡回复力组成，并与修正的牛顿—拉普森法结合，实现了求解后极限平衡路径中的“阶跃”问题。在弧长法中，每一迭代步的成功实现需要两步：选择合适的外载荷增量和选择合适的迭代方法以尽快回复平衡力。

图1 弧长法Fig.1 Arc-length method

2 材料腐蚀、疲劳裂纹预报模型

2.1 材料腐蚀预报模型

本文考虑海洋工程结构中最常见的均匀腐蚀。均匀腐蚀下，结构材料的年平均腐蚀厚度为

式中：ri为平均年腐蚀率（mm/年）；t0为防腐材料的保护时间。

2.2 疲劳裂纹预报模型

现有关于裂纹扩展的研究多是应用断裂力学中的裂纹扩展方程把裂纹的大小定义为时间的函数。本文采用Pairs-Erdogen公式来预报结构裂纹扩展尺寸：

式中：a为裂纹长度，N为应力循环次数；Δσ为应力范围，ΔK为应力强度因子；Y（a）为几何因子，可假设Y（a）=Y为一常量。

对（2）式积分，得

式中：a0为初始裂纹长度，C为常数，可近似为符合对数正态分布。

2.3 材料腐蚀、疲劳裂纹影响下极限强度分析方法

材料腐蚀的存在，导致结构构件壁厚削减。而当裂纹达到一定长度时，则会降低结构的极限强度，强度的减小又将在一定程度上增加名义应力水平，导致裂纹扩展，从而减小了整个平台结构的极限强度。同时，由于腐蚀、裂纹等的发生和发展，平台结构的极限强度是随服役年限不同而变化的，可认为是一个腐蚀速度ri（t）和裂纹长度a（Nt）的函数

式中：ri（t）为由于腐蚀而减少的管壁厚度，a（Nt）为在载荷周期数内的裂纹长度。

本文采用弧长法求解，考虑几何和材料非线性[10]的影响，通过改变单元大小、载荷步长、边界条件等影响结果精度的因素，得到准确的平台弯矩—曲率，载荷—位移曲线，从而获得平台在考虑腐蚀、裂纹影响下的关键结构极限强度。具体计算流程如图2所示。

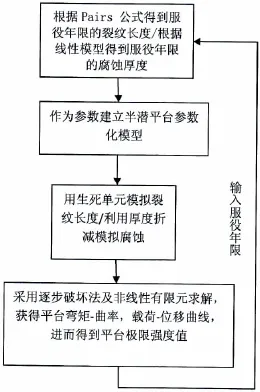
图2 结构损伤下极限强度计算流程Fig.2 Calculation flow of the ultimate strength in the damage of structures

3 数值仿真分析

3.1 关键部位的选取

以我国自主建造的第六代深水半潜式钻井平台为算例，该平台最大作业水深3 000 m，钻井深度可达10 000 m。目标平台的主体结构为一双下浮箱、四立柱、箱型甲板、艏艉立柱间各用2根横撑连接的框架结构，平台总长度114．07 m，宽度78．68 m，高度（基线到主甲板）38．2 m。根据整体半潜式平台的强度计算结果，选取应力较大部位作为关键节点和关键构件作为研究对象。通过sesam软件进行分析搜索，取半潜平台应力较大的最大作业工况为分析工况。该工况参数为波高9 m、周期9.5 s、浪向-90°、相位角-32°，半潜式平台应力分布如图3所示。图3计算结果表明，较大应力位置出现在立柱和横撑的连接处，因此选取该平台的两个部位作为关键结构进行研究，包括：（1）立柱和横撑的连接处作为关键节点模型；（2）整个横撑结构作为关键构件模型。

图3 半潜式平台应力分布图Fig.3 Stress distribution of semi-submersible platform

3.2 服役期海洋平台关键构件和节点腐蚀及裂纹预报

假设平台主要结构的腐蚀及裂纹发生在平台服役5年之后，结构腐蚀速率取水面以下的构件以0．15 mm／a的平均速度在横撑外侧发生腐蚀，暴露在大气中的构件以0．05 mm／a的平均速度在横撑外侧发生腐蚀[11]。根据公式（1）可计算平台不同服役年限下腐蚀厚度，计算结果如图5。根据pairs公式计算平台不同服役年限下裂纹长度，假设平台服役五年后的应力较大部位（如图6、图7所示位置）产生了疲劳裂纹，初始裂纹长度为0.5 mm，根据公式（2）进行不同服役年限疲劳裂纹扩展长度的预报，其中动应力幅值Δσ根据半潜平台有限元计算结果为32.6 MPa，C=1.07e-11，a0=0.5，Y=1[12]。裂纹随服役年限的扩展计算结果如图4所示。

图4 平台全寿命期内裂纹扩展曲线Fig.4 Curve of crack growth in total life cycle

图5 平台全寿命期内腐蚀厚度曲线Fig.5 Curve of corrosion in total life cycle

3.3 计及腐蚀、裂纹损伤的关键部位参数化有限元模型

3.3.1 参数化有限元模型及边界条件

平台关键部位的材料为EQ36钢材，屈服强度为355 MPa，密度为7 800 kg／m3，泊松比为0.32，弹性模量为206 GPa。整个结构采用SHELL143单元模拟横撑板结构，采用BEAM188单元模拟加强筋结构，在裂纹处对有限元网格进行细化。

由于横撑跨度较大，且为左右对称结构，为减小计算量，关键构件模型取横撑的一半进行参数化建模，左侧对称端面采用对称约束。关键构件模型共划分22 668个单元，21 266个节点。根据实际情况，立柱板四周采用刚性约束，有限元模型如图6所示。

建立关键节点有限元模型时，将立柱上端离横撑延长1 m，下端与浮体甲板相交来消除其两端边界的影响；横撑分别向立柱外测延长2个肋位（1 552*2 mm）距离，内侧延长1个肋位（1 552 mm）距离以消除边界条件的影响。关键节点模型共划分53 169个单元，50 971个节点。立柱上下端采用刚性约束，有限元模型如图7所示。

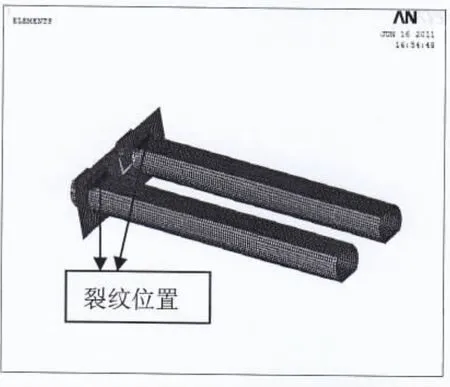
图6 关键构件有限元模型Fig6 FE modal of key component

图7 关键节点有限元模型Fig7 FE modal of key joint

按照MPC法原理，采用刚性梁连接端面节点，在刚性梁交接处施加载荷。首先对结构进行一阶屈曲分析，得到结构的理论屈服强度，将理论屈服强度的1.2-1.5倍作为载荷施加于结构上，进行关键构件极限强度计算。

3.3.2 结构腐蚀损伤的模拟

根据不同服役年限计算出腐蚀厚度，在有限元模型中将相关构件厚度进行折减来模拟不同服役年限、不同结构部位的腐蚀情况，本算例不考虑对结构腐蚀的修复。

3.3.3 疲劳裂纹的模拟

计算不同服役年限的裂纹扩展尺寸，通过采用ANSYS软件中生死单元技术实现有限元模型裂纹的模拟，本算例不考虑对结构裂纹的修复。

3.4 关键部位失效模式的确定

半潜平台的整体应力分析结果表明，结构的受力方式主要有轴向受压、受弯以及受剪，在多数情况下，关键结构部位属于多种受力状态联合作用，而且在平台受到不同海况作用下，结构的主受力方式不完全相同，根据本项目选取的计算工况，关键构件以受弯为主，关键节点受剪切力较大，因此对于关键构件主要分析受弯失效时的极限强度、对于关键节点主要计算剪切失效时的极限强度，同时为了研究不同服役年限下腐蚀和疲劳裂纹对局部结构极限承载力的影响，分别计算了平台结构在无损状态及服役5年、10年、15年、20年、25年、30年、35年、40年、45年和50年关键部位的极限承载力。

3.5 全寿期极限承载力

3.5.1 无损状态

关键构件受弯极限承载力如图8所示，关键节点受剪极限承载力如图9所示。

关键构件无缺陷状态下受弯失效模式下的极限承载力为6.127 e5 kN.m，关键节点在无缺陷状态下受剪失效模式下的极限承载力为1.408e5 kN。

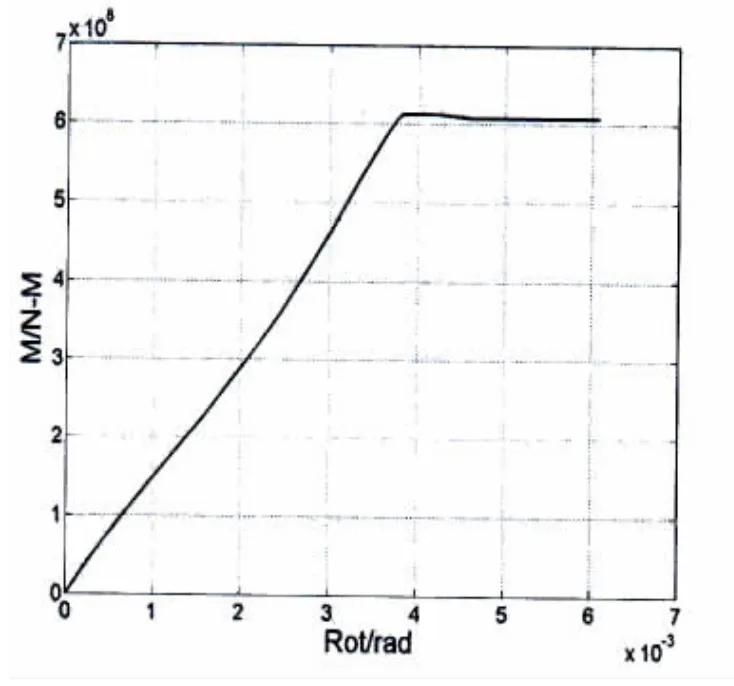
图8 关键构件无损受弯极限强度Fig.8 Moment-curvature relationship of key component on the whole

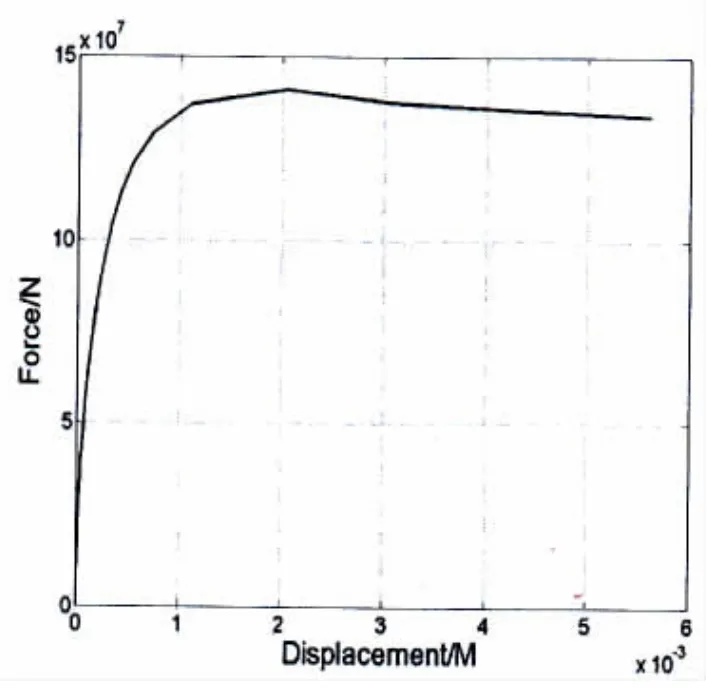
图9 关键节点无损受剪极限强度Fig.9 Moment-curvature relationship of key joint on the whole

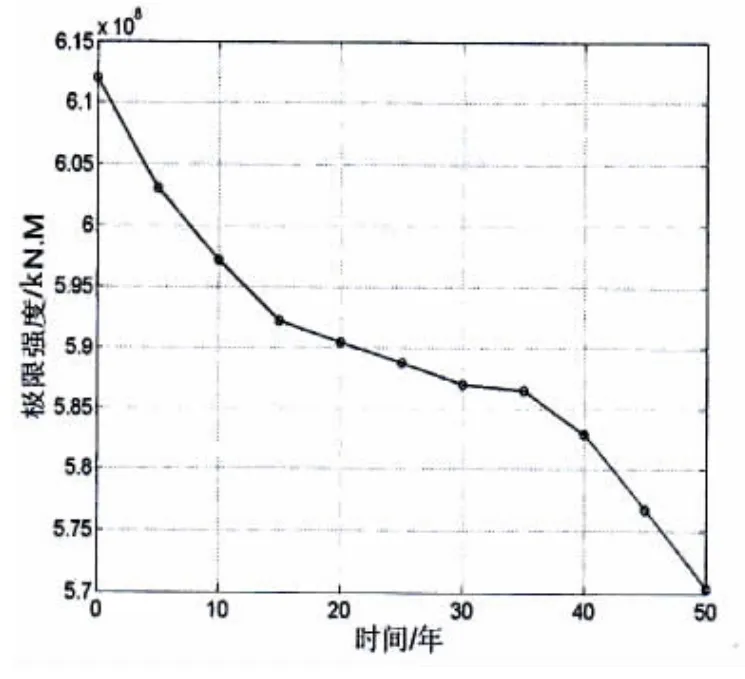
图10 关键构件在裂纹损伤下极限强度随服役年龄的变化Fig.10 The ultimate strength of key component varying with time in the crack-damage

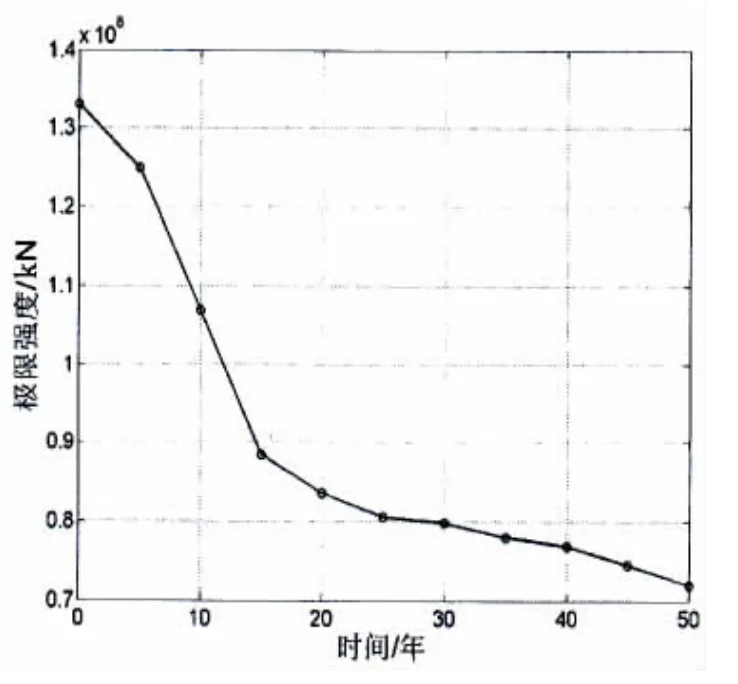
图11 关键节点在裂纹损伤下极限强度随服役年龄的变化Fig.11 The ultimate strength of key joint varying with time in the crack-damage

图12 关键构件在腐蚀损伤下极限强度随服役年龄的变化Fig.12 The ultimate strength of key component varying with time in the corrosion-damage

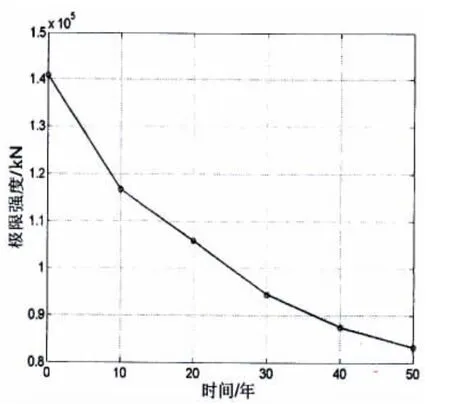
图13 关键节点在腐蚀损伤下极限强度随服役年龄的变化Fig.13 The ultimate strength of key joint varying with time in the corrosion-damage

3.5.2 不同服役期极限承载力

本文分别研究了裂纹损伤和腐蚀损伤对结构极限承载力的影响。根据本文所建立的全寿期极限强度计算方法以及关键构件和节点的参数化模型，通过计算可获得不同服役年限下极限承载力。图10-11给出了平台在裂纹损伤下的每个服役期的极限强度，图12-13给出了平台在腐蚀影响下的每个服役期内的极限强度。上述计算结果表明半潜式平台的极限强度随役龄的增加呈递减趋势，但结构腐蚀损伤和裂纹损伤对结构的极限承载力的影响程度和趋势有所不同。在结构腐蚀影响下，不同位置结构极限承载力的降低程度较为一致，服役50年后，关键构件和关键节点极限强度分别降了41.1%和37.5%；而裂纹损伤对不同构件的结构极限承载力的影响程度差别较大，服役50年后，平台关键构件的极限强度下降了6.9%；平台关键节点的极限强度下降了45.9%。

3.6 腐蚀，裂纹共同作用下的极限强度预报

为了分析裂纹和腐蚀共同作用下对结构极限承载力的影响，本文选取平台服役30年时进行研究。表1给出了腐蚀、裂纹单独作用下与共同作用下，平台关键节点和关键构件极限力计算结果。

表1 服役30年腐蚀和裂纹单独和共同作用下的结构极限承载力Tab.1 The ultimate strength on cooperation of corrosion and crack damage when service 30 years

比较腐蚀和裂纹对极限强度的影响，对于关键构件受弯状态而言，材料腐蚀较疲劳裂纹对关键构件极限强度的影响更大；对于关键节点受剪状态而言，疲劳裂纹较材料腐蚀对关键节点的极限强度影响更大。

4 结论

本文开展了第六代半潜式钻井平台全寿命期关键部位极限强度预报方法研究，针对半潜式平台局部结构，考虑不同服役年限材料腐蚀、疲劳裂纹的影响，建立了局部参数化有限元模型，发展了一种适用于平台结构全寿期极限强度的预报方法，并应用于深水半潜式钻井平台关键节点和关键构件极限强度分析，得到如下结论：

（1）结构腐蚀会使平台结构极限承载力随服役年限的增加呈近线性递减的趋势，而且对不同位置结构极限承载力的影响程度较为一致。服役50年后，关键构件和关键节点极限强度分别降了41.1%和37.5%，说明腐蚀对平台的极限强度产生了重要的影响，在平台结构全寿命期安全性评估中应予以考虑；

（2）疲劳裂纹对不同位置结构极限承载力的影响程度变化较大，如服役50年后，在疲劳裂纹影响下，关键构件和关键节点极限强度分别下降6.9%和45.9%，因此疲劳裂纹对关键节点极限承载力的影响更为显著。同时由于疲劳裂纹随服役年限增加而逐渐扩展，平台结构极限承载力也随服役年限的增加呈递减趋势，但在不同服役阶段递减速率有所不同，在服役期前15年和服役后期35-50年内极限强度递减速度较快，在服役中期极限强度递减速度较慢。

（3）比较腐蚀和裂纹对极限强度的影响，对于关键构件受弯状态而言，材料腐蚀较疲劳裂纹对关键构件极限强度的影响更大；对于关键节点受剪状态而言，疲劳裂纹较材料腐蚀对关键节点极限强度影响更大。

（4）本文在计算疲劳裂纹长度和腐蚀厚度时，把腐蚀和裂纹作为相互独立的变量考虑，在实际情况中，腐蚀和裂纹相互影响，对结构的极限强度有一定的影响，因此应予进一步研究分析。

[1]Petrusja D J,Berek E P,Ingerollrw,Valdivieso J B.Assessment of vermillion 46-A platform[C]//Offshore Technology Conference 7474.Houston,Texas,1994.

[2]Nie Binglin.How to evaluate the safety of jacket platform in chendao oilfield[J].China Offshore Platform,2005,20(4): 44-47.

[3]Xie Wenhui,Xie Bin.Local strength analysis for typical joints of deepwater semi-submersible rig[J].China Offshore Oil and Gas,2010,22(4):265-269.(in Chinese)

[4]Wang Shengnan,Yu Hongyan.Application of limit analysis to the determination of load-carrying capacity of structures with cracks[J].Mechanical Science and Technology,2004,23(7):863-866.(in Chinese)

[5]Paik J K,Anil K,Thayamballi P.Ultimate strength of ship hulls under torsion[J].Ocean Engineering,2001,28(8):1097-1133.

[6]Paik J K.Residual ultimate strength of steel plates with longitudinal cracks under axial compression-nonlinear finite element method investigations[J].Ocean Engineering,2009,36(3-4):266-276.

[7]Paik J K.Residual ultimate strength of steel plates with longitudinal cracks under axial compression-experiments[J].O-cean Engineering,2008,35(17-18):1775-1783.

[8]Ji Chunyan,Li Shanshan,Cheng Minglu.A global reliability assessment method on aging offshore platforms with corrosion and cracks[J].China Ocean Engineering,2009,23(2):211-220.

[9]刘相新,孟宪颐.ANSYS基础与应用教程[M].北京:科学出版社,2006.

[10]Zhang Jianbo,Zeng Changke,Xiao Xi.Ultimate strength analysis of semisubmersible platform[J].China Offshore Platform, 2005,20(3):19-22.(in Chinese)

[11]Melchers R E.Corrosion uncertainty modeling for steel structures[J].Journal of Constructional Steel Research,1999,52 (1):3-19.

[12]陈传尧.疲劳与断裂[M].武汉:华中科技大学出版社,2002.

A prediction method of the ultimate strength of key components of semi-submersible platforms in total life cycle

JI Chun-yan1,YU Wen1,HUANG Shan2,ZHANG Jian1
(1.Jiangsu University of Science and Technology,Zhenjiang 212003,China;2.University of Strathclyde, the City of Glasgow,UK)

Based on the progressive collapse analysis method and finite element method,a calculation method of the ultimate strength of Key Component and Key Joints of semi-submersible platform in total life-cycle was developed,which considered the structural damage such as material corrosion and fatigue cracks.Selecting the cross brace and stand column of 3 000 m semi-submersible platform as a computational model,combining ANSYS software to establish a parametric finite element model by taking corrosion thickness,crack size as the variational parameters,the ultimate bearing capacity of key structure of semi-submersible platform in different service lives was calculated.On this base,the injury factors in total life cycle such as corrosion and fatigue cracks,and so on were considered,and the ultimate bearing capacity of key structure changing with platform age in total life cycle was given.

semi-submersible platform;Key Component;Key Joints;ultimate strength;fatigue crack;corrosion

P75

A

10.3969/j.issn.1007-7294.2015.05.011

1007-7294（2015）05-0566-08

2014-07-25

嵇春艳（1976-），女，教授，E-mail：jichunyan.jkd@163.com；于雯（1989-），女，硕士。