基于功率流法的振动与声辐射研究
李广,吴文伟
(中国船舶科学研究中心,江苏无锡214082)
基于功率流法的振动与声辐射研究
李广,吴文伟
(中国船舶科学研究中心,江苏无锡214082)
文章以水中有限长加肋圆柱壳为研究对象,利用模态叠加法导出了在点激励作用下壳体中传播的功率流表达式,以及辐射声功率的表达式,提出了辐射因子,通过数值算例探索了三种振动波功率流在不同频段及不同位置的传播特性,并在不同频段对传播功率流作了一定简化,进一步分析了其能量传播规律。
模态叠加法;功率流;声辐射
0 引言
有限长弹性圆柱壳被广泛应用于船舶、航空及石油工程等各个工程领域,因此研究其振动与声辐射特性对工程实际应用具有重要指导意义。国内外学者对有限长圆柱壳结构的振动与声辐射进行过大量的研究:Harari等[1]研究了具有任意边界条件的水下有限长加肋圆柱壳体的振动与声辐射;汤渭霖等[2]得到了有限长加肋圆柱壳的振动与声辐射的近似解析解,并研究了肋骨对声辐射的影响。
自Goyder和White[3-5]于1980年创建功率流理论以来,功率流方法作为一种结构振动的分析方法,被越来越广泛地应用在振动分析中[6-9]。由于功率流既包含力和速度的幅值大小,也考虑了它们之间的相位关系,从而避免了单纯使用速度或加速度有效值表示的振级落差带来的一些问题,并且功率流反映了振动能量的传递,可以获得系统中能量的传递规律。而辐射声可以以声功率的形式来表达,因此,振动与声辐射可以从能量的角度来统一进行研究。
本文旨在以水中有限长加肋圆柱壳为研究对象,以振动功率流与辐射声功率来分别研究振动与噪声,分别得到壳体中弯曲波、纵波、扭转波的振动功率流及其与辐射声功率的关系,以及不同功率流之间的相互影响,为工程中类似结构的减振降噪及测试技术提供一定的指导依据。
1 水中有限长加肋圆柱壳的近似解析解
1.1 计算模型
如下图所示的浸入在水中长为2L的弹性加肋圆柱薄壳,半径为R,壳体厚度为h,h/a<<1,材料密度ρp,杨氏模量E,损耗因子η,泊松比μ,周围流体介质密度ρ0,声速c0,肋骨高度为hr,厚度为dr,间距为d,第j根肋骨位置为xj,薄壳振动可以用中面在x、θ、r方向的位移u、v、w来表示,其中u为轴向位移分量,v为圆周切向位移分量,w为圆周径向位移分量,两端边界条件为简支,即:

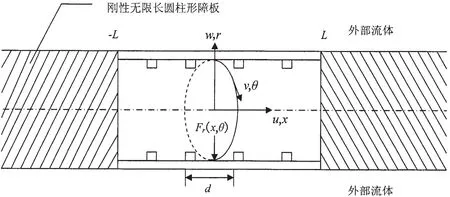
图1 水中简支有限长圆柱壳模型Fig.1 Simply supported finite cylindrical shell immersed in water
1.2 振动方程及其解的形式
假设振动为对称振动,则壳体可以采用Donnell方程来描述:


其解的形式[6]设为:

其中:解的表达式中略去了时间项e-iωt,且该形式解仅适用于对称激励的形式。根据简支边界条件有:

1.3 外部激励力
在这里,只考虑径向激励力,不考虑切向与轴向激励力,将其展开为:

展开系数由下式给出:
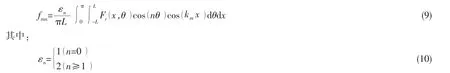
1.4 外部流体介质反作用力
在简谐(e-iωt)情况下,流体介质中的声压p(r,x,θ)满足Helmholtz波动方程及边界条件:

其中:k=ω/c0,同理将圆柱壳表面声压解写为:

文献[6]给出了声辐射负荷引起的表面声压展开系数为:

1.5 肋骨反作用力
肋骨近似为只有径向力g(x,θ)作用,同样地,将g(x,θ)展开为:

高度。
1.6 求解耦合方程
在这里,我们同时略去了方程两端力与位移中的时间项e-iωt,因此对结果并没有影响。将以上驻波形式解、外部径向激励力、流体介质反作用力以及肋骨反作用力代入Donnell方程,得到:
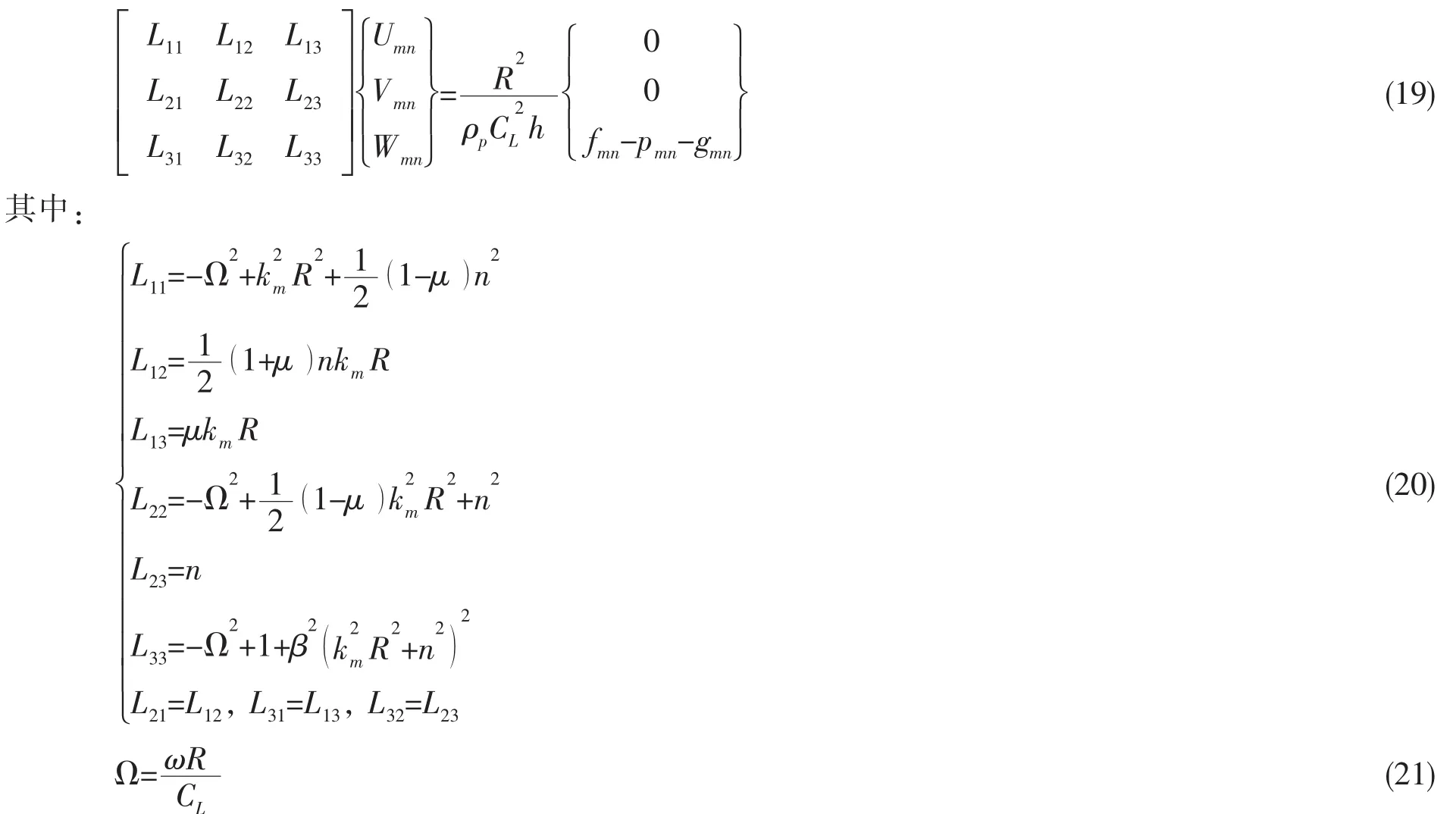
进而得到耦合方程:



以及u(x,θ),v(x,θ),w(x,θ)
2 振动功率流与辐射声功率
2.1 振动功率流
根据壳体微元的应力—应变关系:
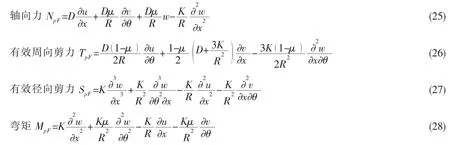
根据振动功率流的定义:

在位于轴向坐标为x的截面上,壳体的各个内力和力矩所传播的功率流分别为:纵波功率流:

扭转波功率流:

弯曲波功率流:
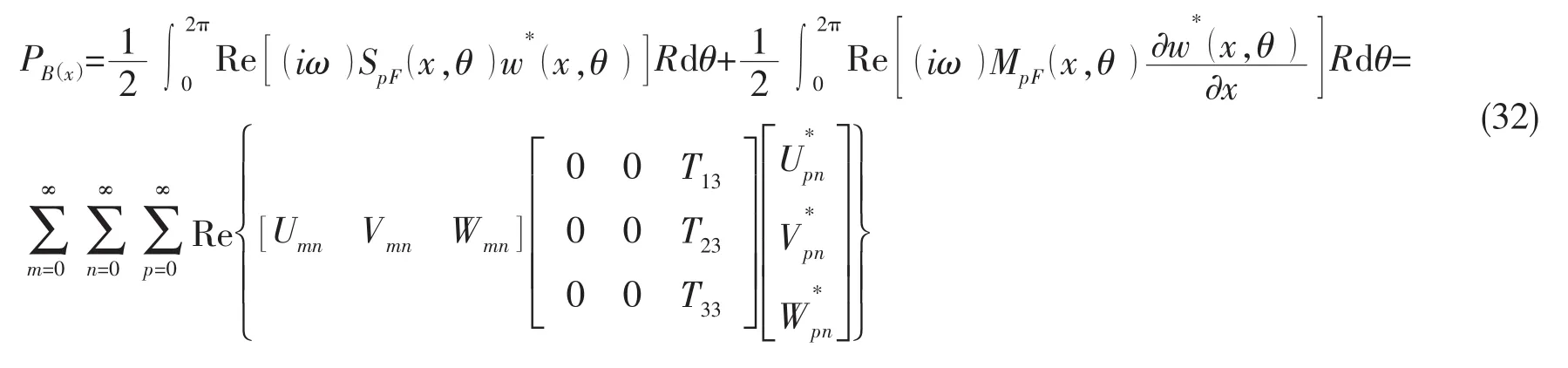
总功率流:

由纵波、扭转波和弯曲波功率流表达式我们可以看出,每一种功率流都包含三部分,而对于纯纵波、纯扭转波以及纯弯曲波功率流而言,它们各自只与相应方向的应力与速度有关,即纯纵波功率流只与轴向速度和轴向力有关,体现在纵波功率流表达式中则只包含项,同理,纯扭转波功率流只与切向速度和切向力有关,体现在扭转波功率流表达式中则只包含项,纯弯曲波功率流只与径向速度和有效径向剪力以及弯矩有关,体现在弯曲波功率流表达式中则只包含项。由此可见,分别表示纵波与扭转波、纵波与弯曲波的耦合作用,其值大小分别通过T21、T31来确定,在确定的模态下,T21和T31随着频率及位置而变化。同理以及也表示相应振动波的耦合作用。
2.2 辐射声功率
根据1.4的壳体表面声压表达式得到辐射声功率为:
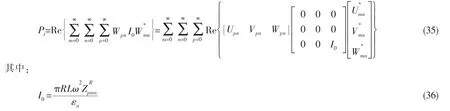
可见三个方向的位移中只有径向位移w可以产生辐射声,对比功率流的表达式,可知在功率流表达式的矩阵T中仅有T33项对声功率产生影响,因此我们可以定义一个辐射因子S(ω),即:

它表示功率流对声功率的影响,其中右端的分母项表示壳体中传播的总纯弯曲波功率流,因此我们就可以通过辐射因子并根据壳体中的纯弯曲波功率流来预报辐射声功率。
3 数值算例及结论
3.1 模型参数
取圆柱壳的基本参数:长度2L=3 m,半径R=0.5 m,厚度h=0.02 m,圆柱壳材料密度ρp=7 800 kg/ m3,杨氏模量E=2.1×1011N/m2,损耗因子η=0.01,泊松比μ=0.3,水的密度ρ0=1 000 kg/m3,水中声速c0=1 500 m/s,肋骨参数:肋骨个数为9个,肋骨间距d=0.3 m,肋骨宽度dr=0.03 m,肋骨高度hr=0.1 m,肋骨材料与壳体材料相同。假设激励力是位于x=0,θ=0处,峰值为1 N的径向集中点激励,方向沿半径指向外部,壳体的环频率约为1 750 Hz。文献[9]表明当L/a>3时,可认为自辐射阻抗远大于互辐射阻抗,忽略互辐射阻抗对计算结果影响不大,因此可令p=m,但忽略互辐射阻抗并不等于忽略流体介质负荷。
3.2 振动功率流的贡献分布
由以上分析可知,每一种功率流分别由三部分构成,一部分是对应方向的力与速度产生的功率流,另外两部分表示其他方向的力产生的耦合作用。取壳体中传播的功率流随位置与频率的变化进行研究。图2~4给出了由激励点向两端传播的纵波、扭转波和弯曲波功率流的贡献分布。
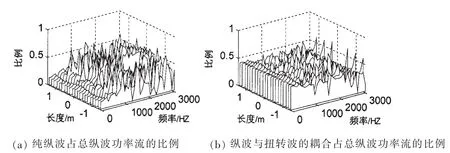
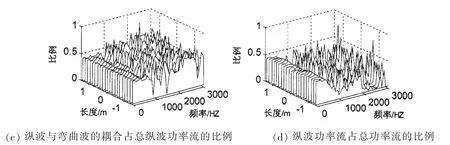
图2 纵波功率流的贡献分布Fig.2 Distribution of longitudinal wave power flow ratio
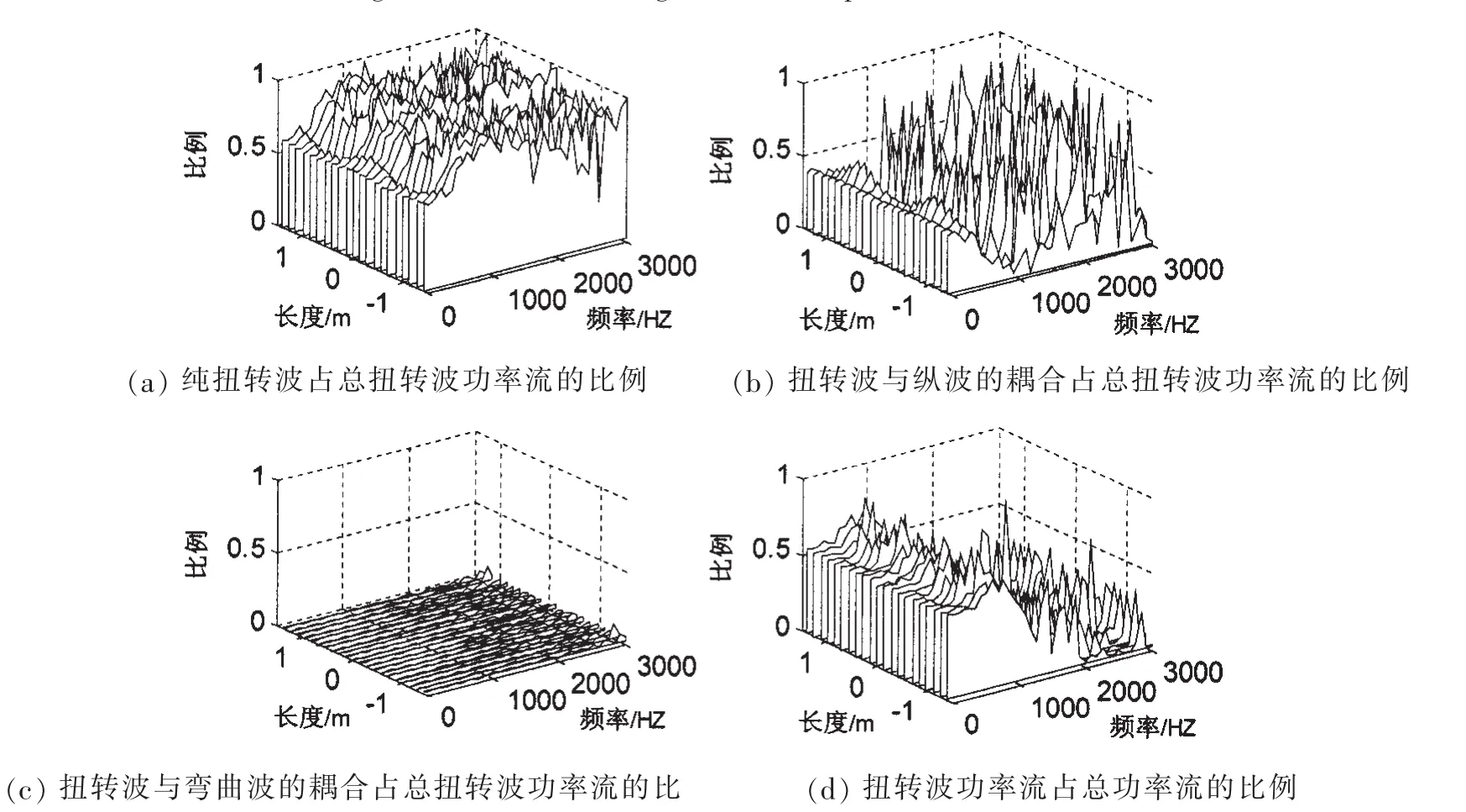
图3 扭转波功率流的贡献分布Fig.3 Distribution of torsional wave power flow ratio

图4 弯曲波功率流的贡献分布Fig.4 Distribution of bending wave power flow ratio
由图2~4我们可以得出以下结论:
(1)在低频段纵波功率流与扭转波功率流占主导,而在中高频段则以弯曲波功率流占主导;
(2)由图2可知,在整个频率范围内,纵波受到其余两种波的影响都较大,尤其是在500 Hz以下的低频段;
(3)由图3可知,不论是在低频段还是高频段,扭转波受弯曲波的影响都很小,可以忽略不计,因此,可以令T32=0;
(4)由图4可知,在超过800 Hz的频段,弯曲波受纵波和扭转波的影响都很小,可以忽略不计,因此,可以令T13=0和T23=0;
(5)对比图2(d)、图3(d)以及图4(d)可知,在500 Hz以下的低频段,弯曲波功率流对总功率流的影响很小,可以忽略不计,而在超过环频率1 750 Hz后,弯曲波功率流成为功率流的主要部分,其次是纵波,扭转波所占的比例最小;
(6)由(2)、(3)和(4)的分析可知,在500 Hz以下的低频段,功率流表达式(33)可以写为:

由(3)和(4)的分析可知,在大于800 Hz且小于环频率的频段内,功率流表达式可写为:
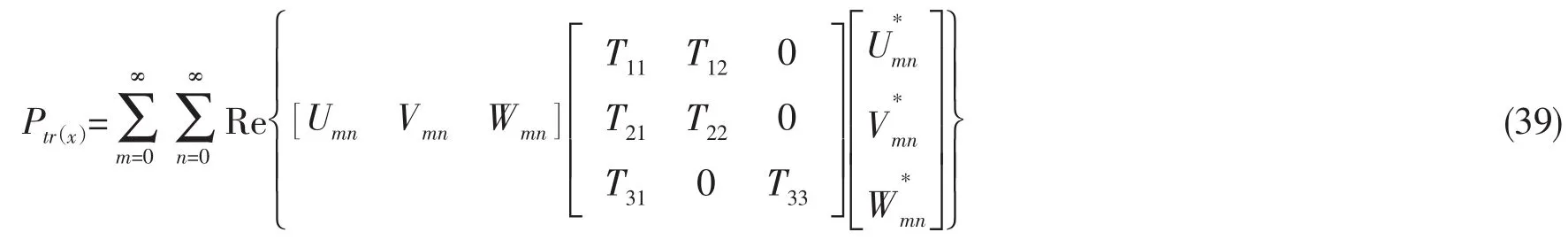
由(5)的分析可知,当频率超过环频率后,功率流表达式可近似写为:
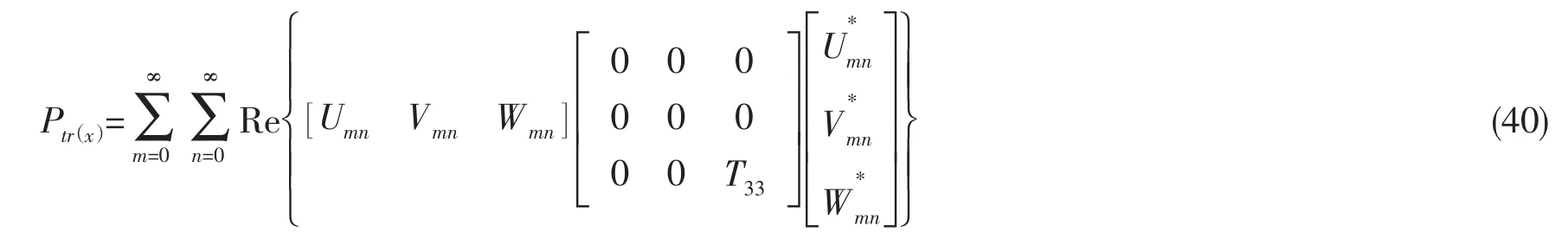
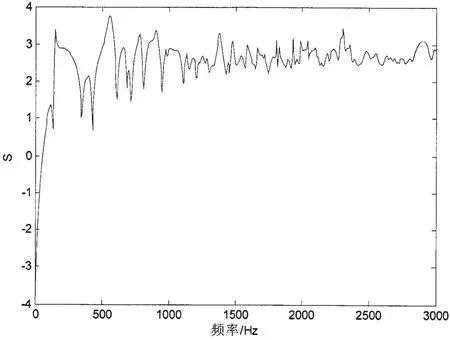
图5 辐射因子Fig.5 Radiation factor
即:

3.3 辐射因子
根据2.2的分析,得到辐射因子随频率的变化曲线,如图5所示。其中,图中的纵坐标取对数。由图中辐射因子随频率的变化曲线,在已知纯弯曲波功率流PB′(ω)后可依据该曲线对辐射声功率进行预报,即:

4 结论
由以上分析可知,在工程实际应用中,若需要测量加肋圆柱壳中功率流的传播,在某些频率范围内可以忽略某些形式的振动波,例如在上述算例中,在500 Hz以下频率范围内,只需测量纵波与扭转波功率流,而在环频率以上范围,如果只需定性分析传播功率流的特性,近似地可以只测量弯曲波功率流。而辐射因子则可以根据壳体中传播的纯弯曲波功率流来预报辐射声功率。因此,本文能够为实际工程测试及噪声预报提供一定的指导依据。
[1]Harari A,Sandman B E.Radiation and vibrational properties of submerged stiffened cylindrical shells[J].J Acoust.Soc. Am.,1990,88(4):1817-1830.
[2]汤渭霖,何兵蓉.水中有限长加肋圆柱壳体振动和声辐射近似解析解[J].声学学报,2001,26(1):1-5. Tang Weilin,He Bingrong.Approximate analytic solution of vibration and sound radiation from stiffened finite cylindrical shells in water[J].Acta Acustica,2001,26(1):1-5.
[3]Goyder H G D,White R G.Vibration power flow from machines into built-up structures,Part I:introduction and approximate analysis of beam and plate-like foundations[J].Journal of Sound and Vibration,1980,68(1):59-75.
[4]Goyder H G D,White R G.Vibration power flow from machines into built-up structures,Part II:wave propagation and power flow in beam-stiffened plates[J].Journal of Sound and Vibration,1980,68(1):77-96.
[5]Goyder H G D,White R G.Vibration power flow from machines into built-up structures,Part III:power flow through isolation systems[J].Journal of Sound and Vibration,1980,68(1):97-117.
[6]朱翔,李天匀,赵耀,刘敬喜.损伤圆柱壳的振动功率流特性研究[J].船舶力学,2007,11(2):284-292. Zhu Xiang,Li Tianyun,Zhao Yao,Liu Jingxi.Vibrational power flow characteristics of damaged circular cylindrical shells [J].Journal of Ship Mechanics,2007,11(2):284-292.
[7]Kudlicka J.Energy flow axisymmetric elastic waves in a three-layered,trans-tropic-isotropic-transtropi,composite cylinder[J].Journal of Sound and Vibration,2004,277:1093-1100.
[8]Choi W J,Xiong Y P,Shenoi R A.Power flow analysis for a floating sandwich raft isolation system using a higher-order theory[J].Journal of Sound and Vibration,2009,319(1-2):228-246.
[9]Liu Chunchuan,Li Fengming,Fang Bo,Zhao Yang,Huang Wenhu.Active control of power flow transmission in finite connected plate[J].Journal of Sound and Vibration,2010,329(20):4142-4135.
[10]刘涛.水中复杂壳体的声-振特性研究[D].上海:上海交通大学,2002. Liu Tao.Research on sound and vibration characteristics of complex cylindrical shell submerged in water[D].Shanghai: Shanghai Jiaotong University,2002.
Vibration and sound radiation research based on power flow method
LI Guang,WU Wen-wei
(China Ship Scientific Research Center,Wuxi 214082,China)
This paper studies stiffened finite cylindrical shells in water based on modal superposition approach.Expressions of vibrational power flow and sound radiation power are obtained and the radiation factor is proposed furthermore when the shell is excited by a point force.The propagation characteristic of three kinds of vibrational power flow in different bands and positions are also explored through a numerical example.In different bands,the expressions of propagation power flow are simplified in order to analyse the propagation regularity of energy furthermore.
modal superposition approach;power flow;sound radiation
TB532
A
10.3969/j.issn.1007-7294.2015.05.016
1007-7294(2015)05-0609-10
2014-12-25
李广(1986-),男,工程师,E-mail:466786274@qq.com;
吴文伟(1969-),男,研究员。

