超大型浮体模块水弹性响应和结构强度分析
杨鹏,顾学康
(中国船舶科学研究中心,江苏无锡214082)
超大型浮体模块水弹性响应和结构强度分析
杨鹏,顾学康
(中国船舶科学研究中心,江苏无锡214082)
水弹性方法针对超大型浮体的刚度特点,充分考虑了结构变形与流体运动的相互作用,是进行结构安全性分析的有效手段。文章采用水弹性分析方法研究了超大型浮体单模块总体波浪载荷以及结构应力响应。首先基于三维有限元方法分析了模块在真空中的总振动模态,然后结合模态叠加法和边界元法计算了模块在流场里面的谐振和模态响应。在此基础上,研究了各模态下结构的应力响应以及总应力响应,并分析了危险载荷工况,评估了超大型浮体单模块的结构强度,研究结果对超大型浮体单模块结构优化设计和安全性评估具有一定的指导意义。
超大型浮体;水弹性;振动模态;波浪载荷;结构强度
0 引言
超大型浮体尺度巨大,可有多个模块拼接而成,作为海上综合补给基地使用,具有飞机起降、燃油补给、后勤保障和旅游等功能,能用于维护国家的深远海海洋权益。世界上一些发达国家对超大型浮体技术十分重视,2014年1月一些媒体报道了日本很可能重启超大型浮体研究项目并实施建造的新闻。我国政府近几年来也越来越重视海洋权益的维护和海洋资源的开发,超大型浮体的研发将为此提供重要的技术保障。超大型浮体(VLFS)的研究起源于二战时期,日本于上世纪八十和九十年代进行了浮体主要关键技术研究,1995-2000年在浮式机场项目的支持下对VLFS开展了系统性的研究,超大型浮体的水弹性基础理论和预报方法得到了较快的发展。1992年美国启动了移动式离岸基地(MOB)的研究计划。1991年举办了首届VLFS国际会议,之后陆续于1996年(日本)、1999(夏威夷),一些国际大型学术会议(例如ISPOE、OMAE、ISSC、ICHMT)均有大量论文对浮体相关技术进行研究。Ohmatsu(2005)[1]对VLFS的研究工作进行了综述,认为VLFS的各种研究主要集中在以下几个方面:(1)概念设计;(2)水弹性响应;(3)连接器设计和载荷响应;(4)系泊系统;(5)设计和建造;(6)可服役性、耐久性和可维护性;(7)事故和风险评估;(8)环境及生态影响,等等。
超大型浮体的水弹性响应和结构安全可靠性是其设计建造的主要关键技术之一。水弹性力学是研究流体水动力和结构弹性响应之间相互耦合作用的学科,与传统刚体理论相比,能够更加准确地考虑浮式结构物的水动力、运动和载荷响应,因而具有很好的工程实用价值和发展前途。目前水弹性理论及其工程应用的研究主要集中在大型船舶和超大型浮式结构物的运动、波浪载荷、应力响应、疲劳损伤和可靠性等研究方面。吴有生和杜双兴(1995)[2]使用三维线性水弹性力学分析了极大型浮式结构物的运动和连接器的应力响应,其计算结果对连接器的设计具有一定的参考价值。崔维成等[3-5]对超大型浮体的关键技术和动力特性进行了研究综述,其中包括VLFS的水弹性响应、非均匀海洋环境的激励、连接构件上的载荷、系泊装置的动力响应计算、带半潜式消波堤的VLFS动力特性、海啸或孤立波下的动响应、快速数值方法和模型试验技术。闫红梅和崔维成(2003)[6]使用Eatock Taylor提出的一种矩形平板格林函数法分析了超大型浮体的水弹性响应,其计算结果与试验相当吻合,证明了此格林函数可以用于超大型浮体的水弹性分析。金晶哲和崔维成(2003)[7]使用模态函数展开方法和特征函数展开法对超大型浮体的水弹性响应进行了分析,分别计算了结构挠曲变形、弯矩和剪力。宋皓和崔维成(2005)[8]对具有缓变地形的超大型浮体响应使用多重尺度法和常规的有限水深格林函数法势流理论进行了分析,其计算结果与试验吻合较好,证明非均匀海洋环境对超大型浮体的响应有一定的影响。Temarel(2008)[9]对水弹性力学进行了展望,提出水弹性理论的发展要特别考虑非线性的影响。Wu和Cui(2009)[10]对三维线性和非线性水弹性的发展以及试验技术进行了综述。Temarel和Hirdaris(2009)[11]在第五届海洋工程技术水弹性国际会议上对水弹性在船舶和海洋结构物设计方面的理论发展和应用进行了总结。另外Hirdaris和Temarel(2009)[12]讨论了近期一些2D和3D水弹性方法在全非线性流固耦合技术上的应用趋势,包括CFD方法。Seto等(2005)[13]使用混合BEM-FEM流固耦合方法分析了VLFS的水弹性响应。Andrianov和Hermans(2003)[14]将VLFS简化为平板分析了其在不同水深下的水弹性响应。Newman(2005)[15]使用P-FFT边界元方法对VLFS的水弹性运动响应和平均漂移力进行了分析。
由前面的综述可知有不少学者对超大型浮体的水弹性响应进行了分析,但是有不少是使用了平板假设,该理论虽然可以用于设计的初级阶段的性能估算,但是对于复杂的构型设计,例如半潜式,在详细结构设计和深入的性能分析阶段该理论无疑无法满足实际需求。另外也有不少学者直接使用模态叠加法的三维水弹性理论用于超大型浮体的理论分析,但是大量的研究仅仅停留在超大型浮体的运动响应、连接器响应和弯曲载荷层次,而对于超大型浮体的危险载荷工况和结构应力响应分布研究较少,而这方面的研究对超大型浮体的结构设计具有重大的指导意义。超大型浮体一旦出现主要结构失效,将会带来非常大的经济损失、人员伤亡和环境污染等,因此需要通过详细的结构应力响应分析和强度校核来保证超大型浮体具有足够的结构安全可靠性。为了适应中国南海特殊的海洋环境,我们进行了新型超大型浮体的设计,该浮体单模块采用横向浮筒半潜式,这种设计形式不同于传统的纵向浮体半潜平台。同时采用柔性连接器的超大型浮体各个模块之间的结构强度影响较小,连接器只是对结构边界条件有一定的影响,因此首先需要将每个模块单独作为一个结构强度评估单元来研究其结构响应和安全性。另外新型半潜式超大型浮体撑杆是较弱的构件,需要在设计和强度评估中重点关注。本文采用三维线性水弹性力学方法就新型超大型浮体的单模块结构开展水弹性和结构应力响应研究。通过系统地开展不同浪向和波长下的单模块结构水弹性响应研究,获得不同工况下浮体的结构应力分布,识别危险的结构区域和载荷工况,结合危险工况下的结构应力响应校核超大型浮体单模块的结构安全可靠性,这对超大型浮体的设计具有一定的指导意义。
1 水弹性理论基础
假设浮体在波浪载荷作用下的运动和弹性变形较小,而且整个响应系统是线性的,那么基于叠加原理,浮体结构相对其平衡位置的运动和弹性变形可以表示为:

式中:pr(r=1,2,…,m)表示相对于第r阶浮体干模态位移的主坐标分量。
上式中的结构变形响应主坐标pr满足广义线性水弹性力学运动方程[16]:
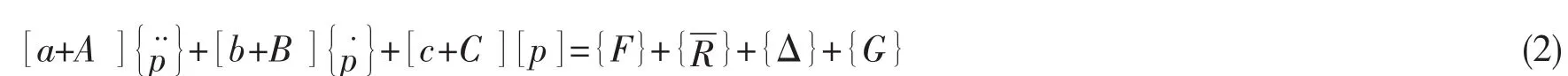
式中:{p}={p1(t),p1(t),…,pm(t)}为广义主坐标向量;[a]、[b]和[c]分别为结构广义质量矩阵、阻尼矩阵和刚度矩阵;[A]、[B]和[C]分别为广义流体附加质量矩阵、附加阻尼矩阵和流体恢复力矩阵;{F}、、{Δ}和{G}分别为广义波浪激励力、广义静态力、广义集中力和广义体积力向量。在研究浮体在波浪中的响应时一般没有广义静态力、广义集中力和广义体积力。
由于以上理论均是基于线性响应系统,因此规则波中的各类响应均可以使用模态叠加法求取[17],例如纵向应力σx:

2 超大型浮体单模块主要参数及生存海况
2.1 浮体单模块主要参数
超大型浮体单个模块的总长为300 m,总宽为100 m,每个单模块浮体均由上部甲板、立柱与下部浮箱组成。图1(a)与图1(b)所示为超大型浮体单模块构型图及水动力模型,整个水动力模型网格约4 000个,以浮体长度方向为x轴,y轴朝左舷,z轴朝上,原点在浮体尾部基线处。

图1 超大型浮体单模块图Fig.1 Single module of VLFS
浮体组成部分的上部甲板、下部浮箱与立柱的尺寸如表1所示,单模块浮体主要参数的数值大小如表2所示。

表1 单模块浮体主要参数Tab.1 Main parameters of single module of VLFS

表2 浮体组成部分尺寸Tab.2 Component scales of VLFS
图2给出了超大型浮体的分段示意图,图中共分为10段,站距为30 m。
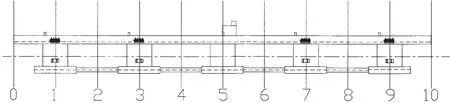
图2 浮体分段示意图Fig.2 Segment draft of VLFS
2.2 生存海况
在超大型浮体概念设计阶段,初步确定将超大型浮体布放于开阔深水海域,选用Jonswap谱,同时设定生存海况的波高、平均跨零周期和谱峰提升因子为(Hs=9.0 m,Tz=12 s,r=2.0)。

图3 短期海浪谱Fig.3 Wave spectrum in short term
3 结构模态分析和主坐标响应
3.1 干模态结果
在使用模态叠加法进行水弹性响应分析时,首先需要正确地建立结构有限元模型,计算获得正确的结构固有频率和相应振型,固有频率从低到高分别为:一节点扭转、二节点垂向弯曲、三节点垂向弯曲和二节点扭转。下图给出了超大型浮体单模块的前4阶弹性模态,其固有频率从2.677~4.957 rad/s。从图中可以看出一节点扭转和二节点垂向弯曲的固有频率非常接近,同时三节点垂向弯矩和二节点扭转的固有频率非常接近,这必然容易产生耦合振动。


图4 单模块结构的干模态振型Fig.4 Dry modal shapes of single module of VLFS
3.2 固有频率和谐振频率
由于结构在流体介质中有附加质量,这会导致结构在流体介质中的固有振动频率发生变化。下表给出了结构在真空中的干结构固有频率和结构在流体介质中的湿结构谐振频率,从图中可以发现谐振频率较固有频率变小了很多,这是因为结构周围附加质量的缘故。浮式结构在流体中的谐振频率对其在波浪作用下的响应十分重要,在谐振频率附近结构响应可能会发生谐振,这对浮体的运动和结构应力响应非常不利。一般来说,在进行浮式结构物的设计时需要将结构谐振频率与海洋波浪能量集中区错开。从图3中可以看出生存工况下的波浪能量主要集中在0.06 Hz附近,超过0.20 Hz后基本没有能量,下表中的结构谐振频率数据显示其最小的谐振频率为0.259 Hz(二节点垂向弯曲),这说明波浪的能量很难直接激起结构谐振。
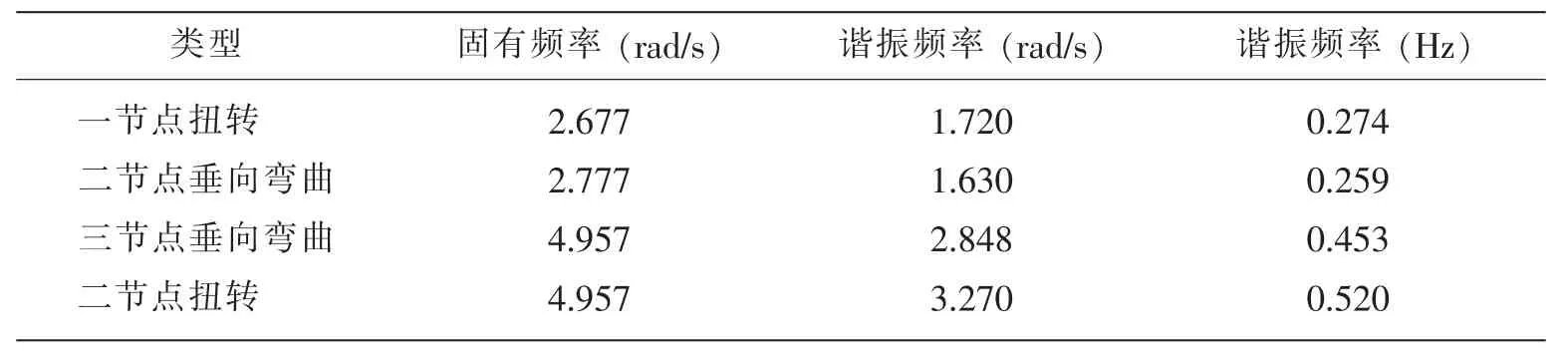
表3 固有频率和谐振频率Tab.3 Natural frequency and harmonic frequency
3.3 主坐标响应
本文利用三维频域水弹性软件THAFTS[16]计算了不同浪向下的结构水弹性响应,其中添加了5%的人工粘性阻尼,使用了前10阶模态,即6个刚体模态和4个弹性模态。图5给出了顶浪无限水深下的计算结果,同时与AQWA的刚体计算结果进行了前六阶运动的比较。
从图5可以看出本文水弹性程序的计算结果在刚体运动部分与AQWA非常吻合,这验证了本文水弹性程序的正确性。从图5(c)中可以发现浮体的Pitch运动在0.385 rad/s(即波长比1.4左右)最大。图5(d)和5(e)中的S1和S2分别代表波浪激励力达到最大和结构谐振频率处谐振响应。


图5 水弹性主坐标响应(顶浪)Fig.5 Principal coordinate responses of VLFS(head sea)

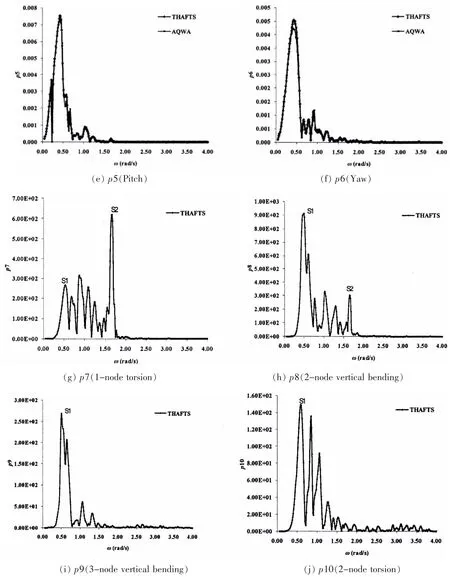
图6 水弹性主坐标响应(40度浪向)Fig.6 Principle coordinate responses of VLFS(40 Deg.)
为了研究结构弹性对浮体位移的影响,图5(f)给出了浮体中纵剖面和中横剖面在上甲板处N3(150,0,27)的垂向位移传递函数。从图中可以看出THAFTS计算得到的刚体结果与AQWA的结果非常吻合,而THAFTS计算的刚体加弹性位移结果与纯刚体结果有一定的差别,弹性位移增加了浮体的总垂向位移,比较明显的差别发生在频率如S1、S2和S3附近,可见在某些波浪频率下,结构弹性变形对结构总垂向位移的影响不可忽略,结构物的位移响应需要在柔性体假设下采用水弹性理论来进行相关分析。
图6给出了40度浪向下各主坐标的响应传递函数,p1~p6代表刚体运动,其与AQWA结果非常吻合。p7和p10代表了斜浪时的浮体结构扭转响应,p8和p9代表了浮体结构的垂向弯矩响应。从p7和p8中发现这些响应均存在多个明显的峰值点,除了在波浪激励力比较大的低频附近(S1点)和结构共振点(S2)外,在两者之间还存在多个峰值。另外在p9(2.848 rad/s附近)和p10(3.270 rad/s附近)中峰值较小,没有明显的共振响应。
4 结构应力响应
由于每个弹性模态反应了该模态的结构位移或应力响应,因此通过公式(3)可以得到结构在外载荷作用下的结构应力响应。图7给出了对每个弹性模态进行质量归一化后的结构应力云图。
选取4#站处上甲板靠舷侧位置N1(120,-42,27)和撑杆底部位置N2(120,-29,1)、5#站处上甲板中纵剖面位置N3(150,0,27)和浮体底部位置N4(150,0,0)作为四个典型位置来考察它们的应力水平。表4给出了归一化弹性模态下各位置应力分布,从表中可以发现z,yz,xz方向的应力响应为0,这是因为所选取的四个位置为shell单元,且单元位于xy平面内。另外p7(1-node torsion)和p10(2-node torsion)模态下N1点的xy向切应力较大,而N3点的为0。对于p8模态,N1和N2点处x与y方向的应力差别较大,而N3和N4点处x与y方向的应力差别较小。

图7 弹性模态下的结构应力分布(Von Mises)Fig.7 Structural stress contours of elastic modals(Von Mises)

表4 质量归一化弹性模态下的各位置应力(Pa)Tab.4 Nodal stress of mass generalized elastic modals(Pa)

续表4

图8 弹性模态下的结构应力分布(顶浪)Fig.8 Structural stress contours of elastic modals(head sea)


图9 弹性模态下的结构应力分布(40度浪向)Fig.9 Structural stress contours of elastic modals(40 Deg.)
图8~9给出了这四个典型位置的应力传递函数,图8(d)和图9(d)中显示当波长平台长度比在1.0左右时Von Mises应力达到最大值。图8和图9中均显示N2、N1、N3和N4的x方向和Von Mises应力依次减小,即撑杆上位置N2的应力最大,浮筒上位置N4的应力最小。图8和图9中结果还显示x方向的应力对Von Mises应力起主导作用。
另外对于0度浪向工况,由于p7和p10的响应为零,因此可以不考虑两个模态下的应力响应,图10给出了0度浪向下N1点和N2点的x向应力合成情况,从图中可以发现对于选取的这两个位置该工况下p8模态下的应力远大于p9模态下的应力,合成的应力基本为p8模态下的应力,可见该浪向下对于这两个位置只需要考虑两节点垂向弯曲模态下的应力分布就可以代表这两个典型结构处的总体结构应力响应。

图10 典型位置的x方向应力传递函数(顶浪)Fig.10 Structural stress RAO of elastic modals in x direction(head sea)
图11(a)中给出了不同浪向下N1点的结构应力传递函数,图中显示0度浪向时的结构应力响应峰值最大(S1点),随着浪向的增加,峰值点对应的波长比逐渐减小,峰值点值也是逐渐减小,除了70度浪向时峰值(S2点)有所增大。图9(b)、(c)和(d)分别给出了不同浪向下N2、N3和N4点的结构应力传递函数,图中显示0度浪向时的结构应力响应峰值最大(S1点),随着浪向的增加,峰值点对应的波长平台长度比逐渐减小,峰值点值也是逐渐减小,除了90度浪向时峰值(S2点)有所增大。

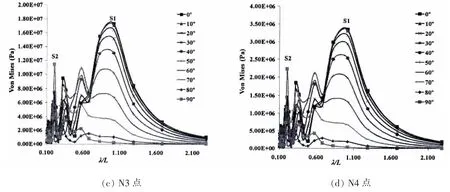
图11 不同浪向下的结构应力传递函数(Von Mises)Fig.11 Structural stress RAO with different wave directions(Von Mises)
图12给出了波长平台长比1.0(波浪周期13.86 s,频率0.072 rad/s)时Von Mises应力随浪向的变化规律,从图中可以看出在同一浪向下N2、N1、N3、N4的应力逐渐减小,同时各点的应力水平从0度到90度逐渐减小。

图12 应力与浪向的关系(波长平台长比1.0)Fig.12 Relationship between stress and wave direction (the ratio of wave length and platform length is 1.0)
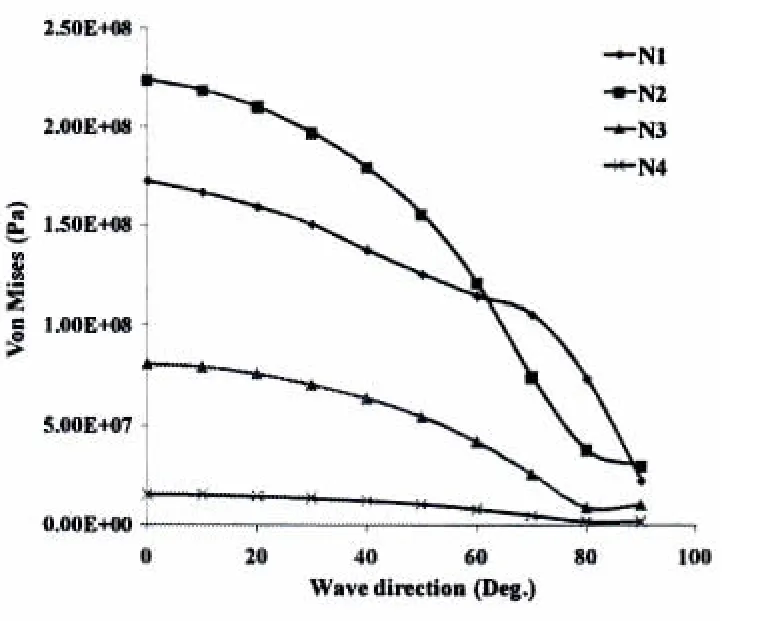
图13 不同浪向的结构应力短期极值Fig.13 Extreme value of structural stress with different wave directions in short-term

表5 不同浪向的结构应力短期极值Tab.5 Extreme value of structural stress with different wave directions in short-term
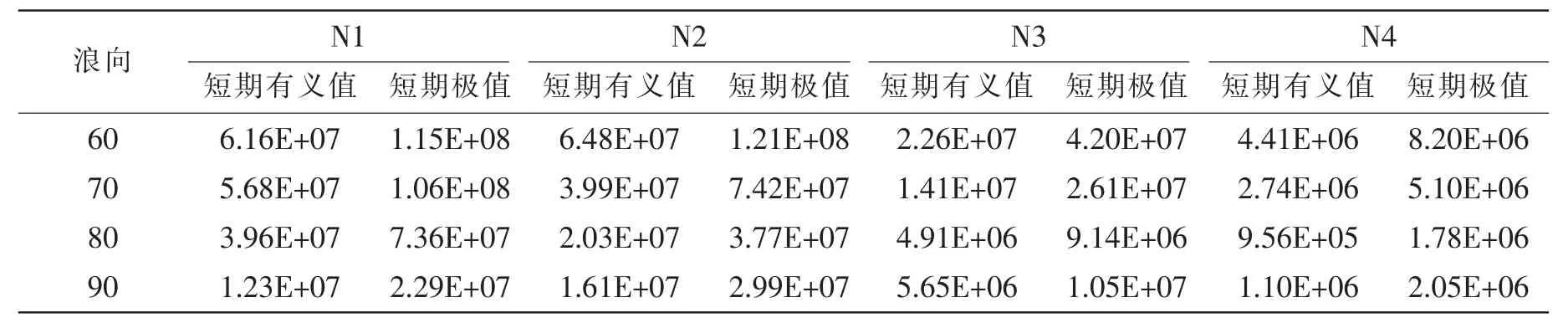
续表5
研究生存海况下浮体结构的应力响应情况对浮体的安全性具有重要意义,本文使用生存海况对典型位置的应力响应做了短期预报,假设短期应力响应幅值服从Rayleigh分布,得到了不同浪向下的短期预报有义值和最可能极值,如图13和表5所示。结果显示0度浪向下结构的应力响应最大,90度最小,随着浪向角增大应力响应逐渐减小。0度浪向下N1、N2、N3和N4的应力极值分别为:173 MPa、224 MPa、80 MPa和16 MPa,这可以看出撑杆上点(N2)应力水平最大,是最危险的结构热点部位。
DNV(2011)[18]的海洋平台规范中给出了如下的许用应力的校核公式:

其中:σeqv为外载荷作用下的结构等效应力响应,σy为材料屈服应力,组合载荷下γm取1.15。本文中撑杆上点(N2)的应力水平σeqv=224 MPa,σy=390 MPa,那么σy/γm=355 MPa,可见文中生存海况下浮体结构拉伸强度满足强度规范要求。
5 结论
本文采用三维线性水弹性力学理论研究了超大型浮体单模块的波浪载荷和结构应力响应。在分析单模块结构干、湿振动模态的固有频率谐振基础上,计算了不同浪向下单模块结构的主坐标响应传递函数和结构总体应力响应特征。通过研究得到以下结论:
(1)超大浮体单模块的弹性响应部分对浮体总位移存在一定的贡献,为了更加真实地获得结构的位移响应,需要在柔性体假设下采用水弹性理论来进行相关分析;
(2)对于文中选取的四个典型位置,不同浪向下的应力响应差别很大,0度浪向(顶浪或随浪)下结构的应力响应最大;
(3)在生存海况下,单模块浮体的结构极值应力响应水平满足船级社相关规范的要求。
综上,本文对一种新型超大型海洋浮式结构物模块的三维水弹性响应进行了分析,研究了其结构应力分布水平和结构强度,这为超大型浮体的设计提供了一定的指导意义。
[1]Ohmatsu S.Overview:Research on wave loading and responses of VLFS[J].Marine Structures.2005,18:149-168.
[2]吴有生,杜双兴.极大型海洋浮体结构的流固耦合分析[J].舰船科学技术,1995,139(1):1-9. Wu Y S,Du S X.Analysis of fluid-structure interaction of VLFS[J].Ship Science and Technology,1995,139(1):1-9.
[3]崔维成,吴有生,李润培.超大型海洋浮式结构物开发过程中需要解决的关键技术问题[J].海洋工程,2000,18(3):1-7. Cui W C,Wu Y S,Li R P.Technical problems in the development of very large floating structures[J].The Ocean Engineering,2000,18(3):1-7.
[4]崔维成,吴有生,李润培.超大型海洋浮式结构物动力特性研究综述[J].船舶力学,2001,5(1):73-81. Cui W C,Wu Y S,Li R P.Recent researches on dynamic performances of very large floating structures[J].Journal of Ship Mechanics,2001,5(1):73-81.
[5]崔维成.超大型海洋浮式结构水弹性响应预报的研究现状和发展方向[J].船舶力学,2002,6(1):73-90. Cui W C.Current status and future directions in predicting the hydroelastic response of very large floating structures[J]. Journal of Ship Mechanics,2002,6(1):73-90.
[6]闫红梅,崔维成,刘应中.超大型浮体水弹性分析的平板格林函数方法[J].海洋工程,2003,21(4):8-22. Yan H M,Cui W C,Liu Y Z.Hydroelastic analysis of VLFS using plate green function method[J].The Ocean Engineering,2003,21(4):8-22.
[7]金晶哲,崔维成,刘应中.预报超大型浮体水弹性响应的模态函数展开方法和特征函数展开方法比较[J].船舶力学, 2003,7(4):86-98. Jin J Z,Cui W C,Liu Y Z.Comparison of modal function expansion method with eigenfunction expansion method for prediction of hydroelastic responses of VLFS[J].Journal of Ship Mechanics,2003,7(4):86-98.
[8]宋皓,崔维成,刘应中.底部呈二维缓变情况下超大型浮体水弹性响应的两种计算方法比较[J].海洋工程,2005, 23(4):1-8. Song H,Cui W C,Liu Y Z.Comparison of two numerical methods for prediction of hydroelastic responses of VLFS on 2D mild variable bottom[J].The Ocean Engineering,2005,23(4):1-8.
[9]Temarel P.Hydroelasticity of ships:Taking stock and moving forward[C]//The 22nd Asian-Pacific Technical Exchange and Advisory Meeting on Marine Structures.Istanbul,Turkey,2008:12-21..
[10]Wu Y S,Cui W C.Advances in the three dimensional hydroelasticity of ships[J].Proc.of the IMechE,Part M Journal of Engineering for the Maritime Environment,2009,223:331-348.
[11]Temarel P,Hirdaris S E(Eds.).Proceedings of the 5th Int.Conference on Hydroelasticity in Marine Technology[C].ISBN: 9780854329045,Southampton,UK,2009.
[12]Hirdaris S E,Temarel P.Hydroelasticity of ships[J].Recent advances and future trends.Proc.IMechE,Part M:Engineering for the Maritime Environment,2009,223:305-330.
[13]Seto H,Ohta M,Ochi M,Kawakado S.Integrated hydrodynamic-structural analysis of very large floating structures(VLFS) [J].Marine Structures,2005,18:181-120.
[14]Andrianov A I,Hermans A J.The influence of water depth on the hydroelastic response of a very large floating platform [J].Marine Structures,2003,16:355-371.
[15]Newman J N.Efficient hydrodynamic analysis of very large floating structures[J].Marine Structures,2005,18:169-180.
[16]Wu Y S.Hydroelasticity of floating bodies[D].Brunel University,U.K.,1984.
[17]Harding R D,Hirdaris S E,Miao S H,Pittilp M,Temarel P.Use of hydroelasticity analysis in design[C]//Hydroelasticity in Marine Technology.Wuxi,China,2006:1-12.
[18]DNV.Design of offshore steel structures,general(LRFD method)[S].DNV-OS-C101,2011.
Analysis on the hydroelastic responses and structural strength of VLFS module
YANG Peng,GU Xue-kang
(China Ship Scientific Research Center,Wuxi 214082,China)
The method of hydro-elasticity considering the fluid and structure interaction could calculate structural safety of floating structures effectively based on the rigid characteristics of very large floating structures(VLFS),which is used here to analyze the global wave loading and structural stress responses of single module of VLFS.In this paper,the natural mode and shape of vibration and intrinsic frequency are calculated by 3D FEM for single module.Then the harmonic frequency and principal coordinate responses of single module are obtained by mode superposition method and BEM method.Forwards,the structural stress responses of each mode and global stress responses are investigated;meanwhile the dangerous loading cases and the structural strength of single module are assessed.The results provide a certain guiding meanings for structural optimized design and safety assessment of VLFS.
very large floating structures(VLFS);hydro-elasticity;vibration modal; wave loading;structural strength
U661.43
A
10.3969/j.issn.1007-7294.2015.05.010
1007-7294(2015)05-0553-13
2014-12-07
国家973基础研究课题(2013CB036105)
杨鹏(1988-),男,博士研究生,E-mail:yangpeng@cssrc.com.cn;
顾学康(1963-),男,研究员,博士生导师。

