一种复杂载荷作用下船舶结构疲劳裂纹扩展预报方法

张鼎，黄小平，崔维成

（1中国船舶及海洋工程设计研究院，上海200011；2上海交通大学海洋工程国家重点实验室，上海200240；3上海海洋大学深渊科学技术研究中心，上海201306）

一种复杂载荷作用下船舶结构疲劳裂纹扩展预报方法

张鼎1，黄小平2，崔维成3

（1中国船舶及海洋工程设计研究院，上海200011；2上海交通大学海洋工程国家重点实验室，上海200240；3上海海洋大学深渊科学技术研究中心，上海201306）

风暴模型是Tomita等提出的用来评估船舶结构疲劳强度的一种随机波浪载荷简化模型，它能表达波浪载荷是与时间相关的随机过程。文中介绍了风暴模型及波浪诱导应力短期分布的基本特征。将风暴模型和裂纹扩展率单一曲线模型及焊趾表面裂纹应力强度因子的计算方法结合起来，探讨了复杂载荷作用下船舶结构疲劳裂纹扩展预报方法。并用权函数法计算了给定残余应力分布的表面裂纹应力强度因子。预报了对接焊接接头焊趾处表面裂纹在风暴波浪载荷作用下的疲劳裂纹扩展行为，结果表明风暴的大小、顺序，初始裂纹尺寸及残余应力对裂纹扩展行为影响明显。合理的风暴模型参数及初始裂纹尺寸的确定对船舶结构的疲劳寿命预报是非常重要的。

风暴模型；波浪诱导应力；单一曲线模型；焊接残余应力；表面裂纹；疲劳裂纹扩展预报

0 引言

船舶在海上航行时，其结构受到波浪载荷作用，受载情况经常变化。若一艘船舶的服役期为20年到25年，那么结构内因波浪作用引起的交变应力的循环次数可达108次之多，这将造成结构的疲劳损伤。常规的疲劳设计过程将波浪载荷视为与时间无关的随机过程。各国船级社提出了疲劳评估简化算法，认为线性波浪载荷产生的应力范围长期分布为Weibull分布，给出了结构不同位置处的Weibull分布形状参数的经验公式[1-3]。然而，波浪载荷的真实序列，应该是一个与时间相关的随机过程[4]。Lin等[5]研究了近海结构宽带谱疲劳应力的时间序列模拟方法。Tomita等[6-8]将船舶在海上航行遇到的波浪情况分为两种：平静海况（calm sea condition）和风暴海况（storm condition），提出了一种随机波浪载荷简化模型—风暴模型，用来表达这种与时间相关的随机过程。风暴的平均浪高，平均持续时间，最大浪高及船舶在服役期间所遇到风暴的数量取决于具体的航线并结合Paris公式进行了船舶节点的疲劳寿命评估。因Paris公式没有考虑裂纹扩展门槛值和平均应力等因素的影响，故不能有效预测复杂载荷作用下结构的疲劳裂纹扩展行为。而黄小平等[9-12]提出的裂纹扩展率单一曲线模型能考虑这些因素的影响并且可直接使用Paris公式中的材料常数，有较好的工程适用性。本文将以裂纹扩展率单一曲线模型结合风暴波浪载荷模型来预报船舶节点的疲劳寿命。主要内容包括：（1）介绍了风暴模型及波浪诱导应力短期分布的基本特征；（2）以风暴模型表述的波浪诱导应力为疲劳载荷，裂纹扩展率采用单一曲线模型，结合焊趾表面裂纹应力强度因子及残余应力引起的应力强度因子的计算方法，给出了一种复杂载荷作用下船舶结构疲劳裂纹扩展预报方法；（3）对一船舶甲板焊接接头焊趾处表面裂纹在风暴波浪载荷作用下的疲劳裂纹扩展行为进行了预报。

1 风暴模型及波浪诱导应力短期分布

1.1 风暴模型简介

Tomita等[6-8]分析了航行于北太平洋航线的38艘船舶及日本—印度航线的11艘船舶在14年间（1976-1989）的航行资料，以及在日本附近的北太平洋海域航行的6艘军舰在3年间（1987-1989）的航行记录，认为船舶在海上航行时遇到的波浪情况可以分为两种：（1）平静海况(calm sea condition)：浪高相对较小，且浪高分布是与时间无关的随机过程；（2）风暴海况（storm condition）：浪高随时间增大，达到最大之后逐渐变小，且浪高分布与时间有关。在实际海况中，以上两种情况随机交替出现，并认为波浪载荷是浪高的线性响应。提出了一种评估船体结构疲劳强度的随机波浪载荷模型—风暴模型，图1为船体结构疲劳强度分析的波浪载荷简化模型—风暴模型。

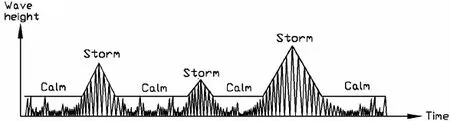
图1 船体结构疲劳强度分析的简化波浪载荷模型—风暴模型Fig.1 Simplified storm model of ship structural fatigue strength analysis

1.2 波浪诱导应力短期分布

在船舶与海洋工程结构中，海洋波浪的长期状态通常看成是由许多短期海况的序列所组成的。每一海况由表征波浪特性的参数以及该海况出现的频率来描述。船舶结构因波浪引起的交变应力过程也可以看成是许多短期海况的序列所组成的。实际应用中，一般是将某一海况中在给定航向下的交变应力过程作为均值为零的窄带平稳随机过程，则根据随机过程理论可知，其应力峰值服从Rayleigh分布。当交变应力过程为窄带时，应力每跨越零均值一次就出现一个峰值，可以假设应力范围Δσ和应力峰值σ之间有以下关系：Δσ=2σ，则应力范围的概率密度函数为[4]：

式中：m0为交变应力过程的功率谱密度GXX（ωe）的零阶矩。对于船舶结构疲劳评估的谱分析方法，波浪的功率谱密度可采用两参数的Pierson-Moskowitz谱（简称P-M谱）。P-M谱用有义波高Hs和平均跨零周期TZ两个参数来表示的表达式为：

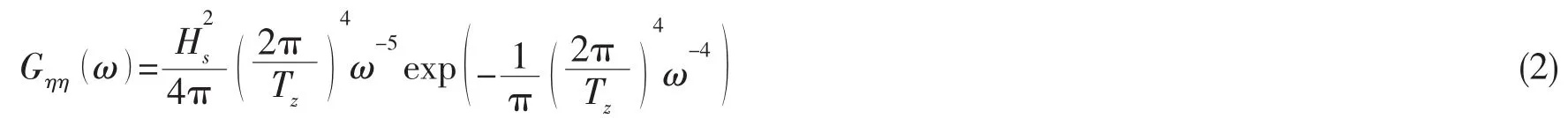
在分析中，实际的响应频率应是遭遇频率ωe，故应力的响应谱为：

式中：Hσ（ωe）为应力响应传递函数，U为航速，θ为航向角，ω为波浪频率。则m0的计算公式为：

2 船舶结构疲劳裂纹扩展预报方法

2.1 裂纹扩展率单一曲线模型

黄小平等[9-12]对变幅载荷作用下结构钢的疲劳裂纹扩展寿命预测时所用到的裂纹扩展率模型中的材料参数的选取进行了研究，提出了等效应力强度因子和单一裂纹扩展率曲线模型，已得到了大量实验数据的验证。其计算公式为：

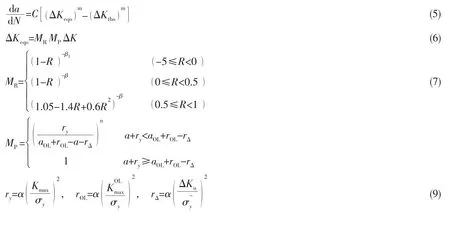
其中：ΔKeqo、ΔKtho是等效于应力比R=0时的等效应力强度因子幅和应力强度因子幅门槛值，（MPa）；C是Paris系数，m是裂纹扩展指数。MR是载荷比的修正因子，MP是载荷次序的修正因子，不考虑超载的影响时MP=1；β，β1是形状系数；ΔKu是低载—过载引起的应力强度因子幅，和是当前循环和前一循环的最小应力强度因子，（是裂纹半长或裂纹深度，（m）；aOL是过载时的裂纹半长或裂纹深度，（m）；ry是裂纹尖端塑性区大小，（m）；rOL是过载时裂纹尖端塑性区大小，（m）；rΔ是低载—过载引起的裂纹尖端塑性区大小的增量，（m）；α是塑性区大小修正系数；n是载荷效应指数。

2.2 焊接接头焊趾表面裂纹应力强度因子

2.2.1 典型焊接接头焊趾表面裂纹应力强度因子计算

当引入应力强度因子放大系数MK来表示焊接缺口应力集中引起的应力强度因子的增加以及考虑焊接残余应力的影响时，焊趾表面裂纹应力强度因子的一般形式可写成如下形式[13]：

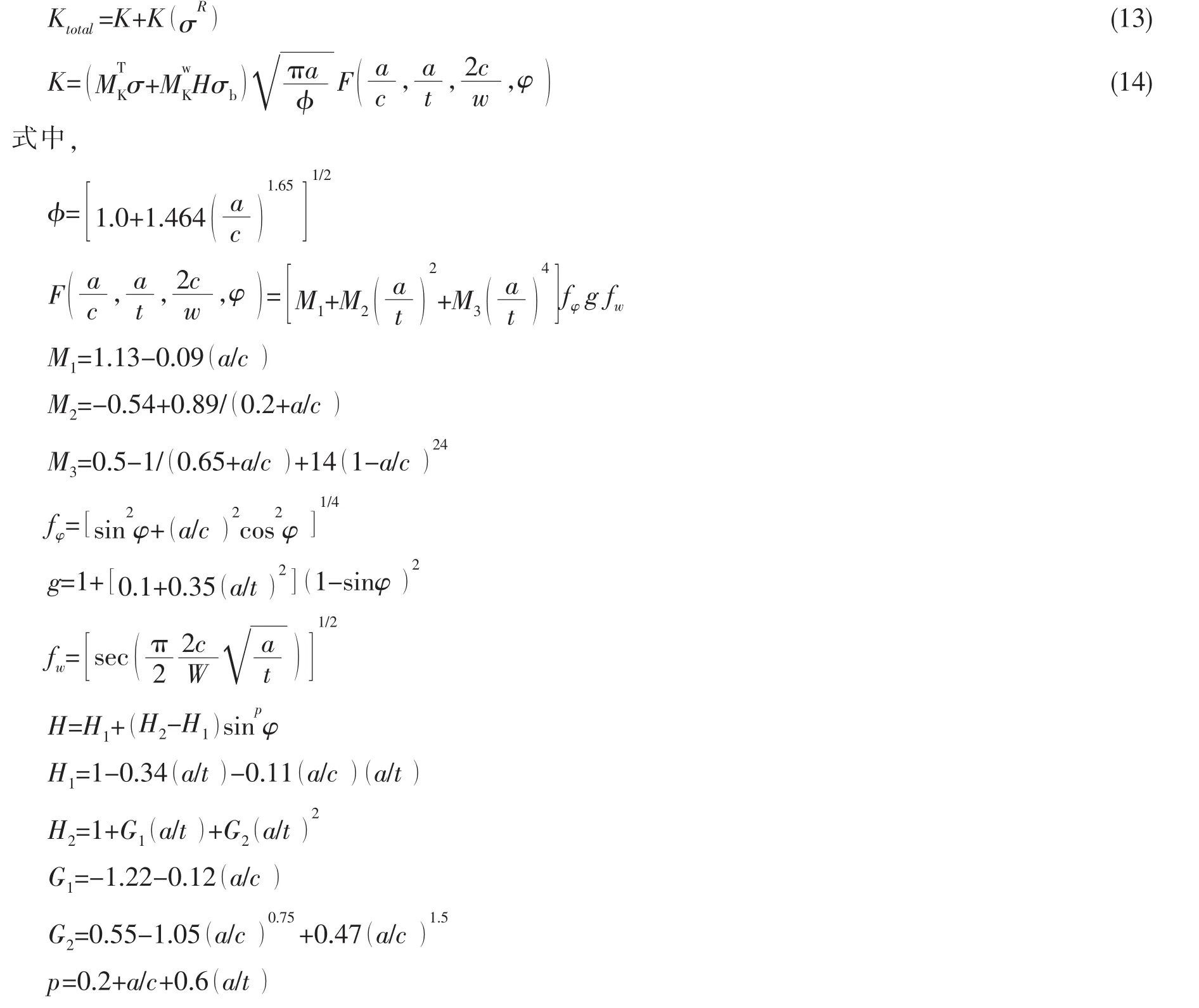
其中：Ktotal，K为总应力强度因子和外载荷引起的应力强度因子；σ为拉（压）应力；σb为弯曲应力；a为裂纹深度；c为裂纹半长；t为板厚；w为板宽；为拉伸应力下焊接结构应力强度因子增大正系数；为弯曲应力下焊接结构应力强度因子增大正系数；K（σR）为残余应力引起的应力强度因子；适用范围：0＜a/c≤1.0，0＜a/t≤1.0，2c/w≤0.5，0≤φ≤π。

当缺陷或裂纹位于局部应力集中区时，在计算K时必须考虑应力集中场的影响，对于焊趾表面裂纹来说，应力强度因子放大系数MK是裂纹尺寸，接头的几何参数以及载荷的函数。对于很浅的表面裂纹，可以认为MK=Kt（应力集中系数）。当裂纹深度增加时，裂纹尖端就逐渐远离应力集中区域，MK随裂纹深度的增加而减小，在厚度为t的平板上的焊接接头，对于对接焊缝，当a/ t=0.1时，MK可认为减小到1.0[14]。对于突出成圆弧形的双面加强高对接接头，其结构简图如图2所示，在MK＞1.0的范围内，这里采用文献[15]给出的对接接头的，计算方法：

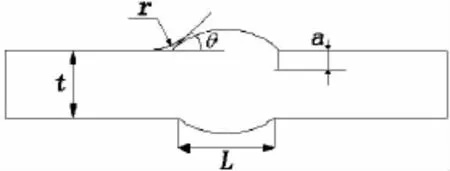
图2 对接接头简图Fig.2 Sketch of weld joint

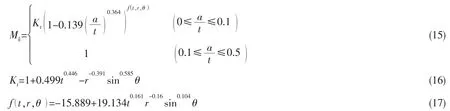
2.2.2 焊接残余应力的分布及其应力强度因子计算

对于平行于焊缝的焊趾表面裂纹，应当考虑垂直裂纹面的焊接残余应力的影响。文献[13]建议垂直焊缝方向的焊接残余应力在焊趾处表面的取值为：

式中：σR为残余应力；σY为材料的屈服强度。

文献[16]给出的焊接残余应力沿板厚度及宽度方向的分布规律的简化形式如图3所示，其中残余应力沿壁厚的分布可表示为：

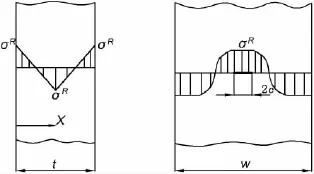
图3 焊接残余应力沿板厚及板宽方向的分布Fig.3 The distribution of welded residual stress along the direction of thickness and width

权函数法是求解任意分布载荷条件下裂纹应力强度因子的一种有效方法，它是由Bueckner[17]和Rice[18]提出的，其求解公式为：

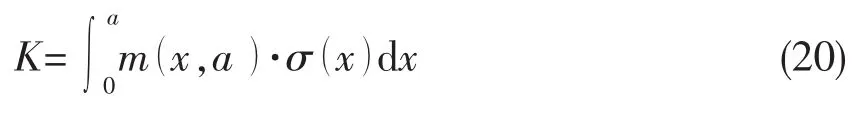
式中：σ（x）为无裂纹体假想裂纹处的应力分布，m（x，a）为裂纹体的权函数。残余应力引起的应力强度因子可根据上述分布按照权函数计算，表达式为：

半椭圆表面裂纹是船舶结构中常见的裂纹形式，对于半椭圆表面裂纹，关心的只是裂纹前沿的扩展速率。因此，为简化计算，只考虑最深点和表面点处的应力强度因子。Wang等[19]利用三维有限元方法计算了深长比（即a/c）小的半椭圆表面裂纹的应力强度因子，并结合Shiratori等[20]给出的深长比大的半椭圆表面裂纹应力强度因子的有限元分析数据及文献[21，22]介绍的边缘裂纹应力强度因子计算方法，给出了半椭圆表面裂纹最深点和表面点处的权函数，其适用范围为0＜a/c≤1.0，0＜a/t≤0.8。具体表达式如下所示：

半椭圆最深点：

半椭圆表面点：

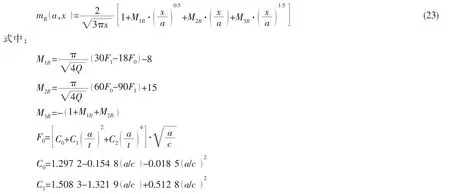
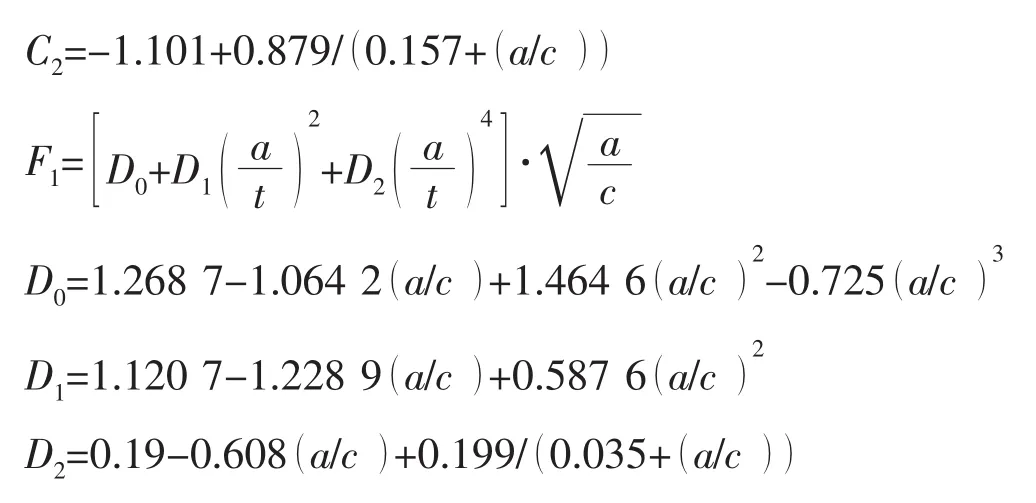
3 实例计算

船舶结构大多为焊接结构，其疲劳裂纹大多起源于焊接接头表面几何非连续性引起的应力集中处，少数起源于焊缝内部较大的焊接缺陷。相关研究和检测表明大多数船舶结构的疲劳热点部位是在构件相互连接的焊缝焊趾处。某船中甲板上有一对接焊接头，其焊缝焊趾处存在表面裂纹，该结构受到用风暴模型表示的波浪随机载荷作用。

3.1 波浪诱导应力分布及应力强度因子计算

根据参考文献[7]，风暴等级按照最大有义波高的大小分为六个等级，如表1所示。平均波浪周期约为6.3 s，每个风暴的持续时间是3.5天（每个风暴有48 000个波浪）。

表1 风暴等级Tab.1 Storm levels

本文旨在给出风暴模型下基于断裂力学的适用于船舶结构疲劳强度评估的方法，这里假定应力响应传递函数为常数，即Hσ（ωe）=30，且取航速U=0，航向角θ=0°。在此基础上本文主要分析了风暴A-风暴E的特征。每个风暴内波浪诱导应力的交变过程可看作是均值为零的窄带平稳随机过程，其应力范围服从Rayleigh分布。根据上文介绍的应力范围短期分布特征，可以得到每种风暴等级的应力范围概率分布函数表达式，如公式（24）-（28）。基于这些函数表达式，在每种风暴情况下，分别利用数学软件工具Matlab产生48 000个服从Rayleigh分布的数据，每个数值即为每个波浪对应的波浪诱导应力范围Δσ，其概率分布如图4所示，循环应力中的最大波浪诱导应力最小波浪诱导应力σwmin以风暴E为例，由于数量较多，只列举了前200个波浪诱导应力范围的分布情况，如图5所示。

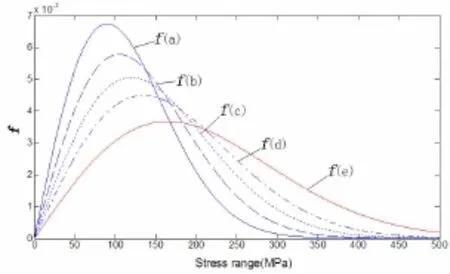
图4 应力范围概率分布图Fig.4 Probability distribution of stress range

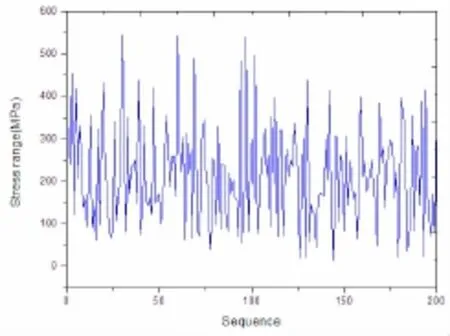
图5 波浪诱导应力范围分布（风暴E）Fig.5 Distribution of wave-induced stress range

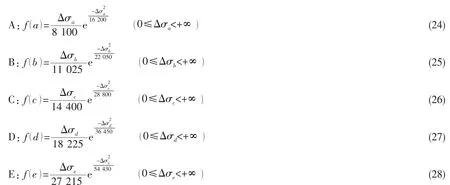
本文选取的结构材料为360 MPa级船舶用钢。其屈服强度为375 MPa，极限强度为491 MPa，应力比R=0时的应力强度因子幅门槛值为单一曲线模型中取C=2.71×10-11，m=3.35， n=0.5。计算应力强度因子时，应考虑两部分应力的合成：波浪诱导应力和焊接残余应力。对于残余应力的处理，目前有两种方法：一种是将残余应力叠加到外载引起的应力上，然后以此计算应力强度因子值；另一种是分别计算由残余应力和外载荷产生的应力强度因子，然后再将两者叠加，本文采用第二种方法。

本文分析的甲板对接接头处受到波浪诱导引起的拉伸应力和弯曲应力的联合作用，但是由于此处的弯曲应力很小，对此处疲劳裂纹扩展的影响很小，可以忽略不计，故本文只考虑拉伸应力的作用。根据（14）式计算由波浪诱导应力引起的最大应力强度因子Kmax及最小应力强度因子Kmin，其中，最大拉伸应力σmax取最大波浪诱导应力σwmax，最小拉伸应力σmin取最小波浪诱导应力σwmin。由上文可知σmax=-σmin，则根据（14）式可以得到Kmax=-Kmin。再按照上文介绍的权函数法计算焊接残余应力引起的应力强度因子K（σR），则载荷比不考虑残余应力的影响时，载荷比R=-1。

3.2 预报结果分析

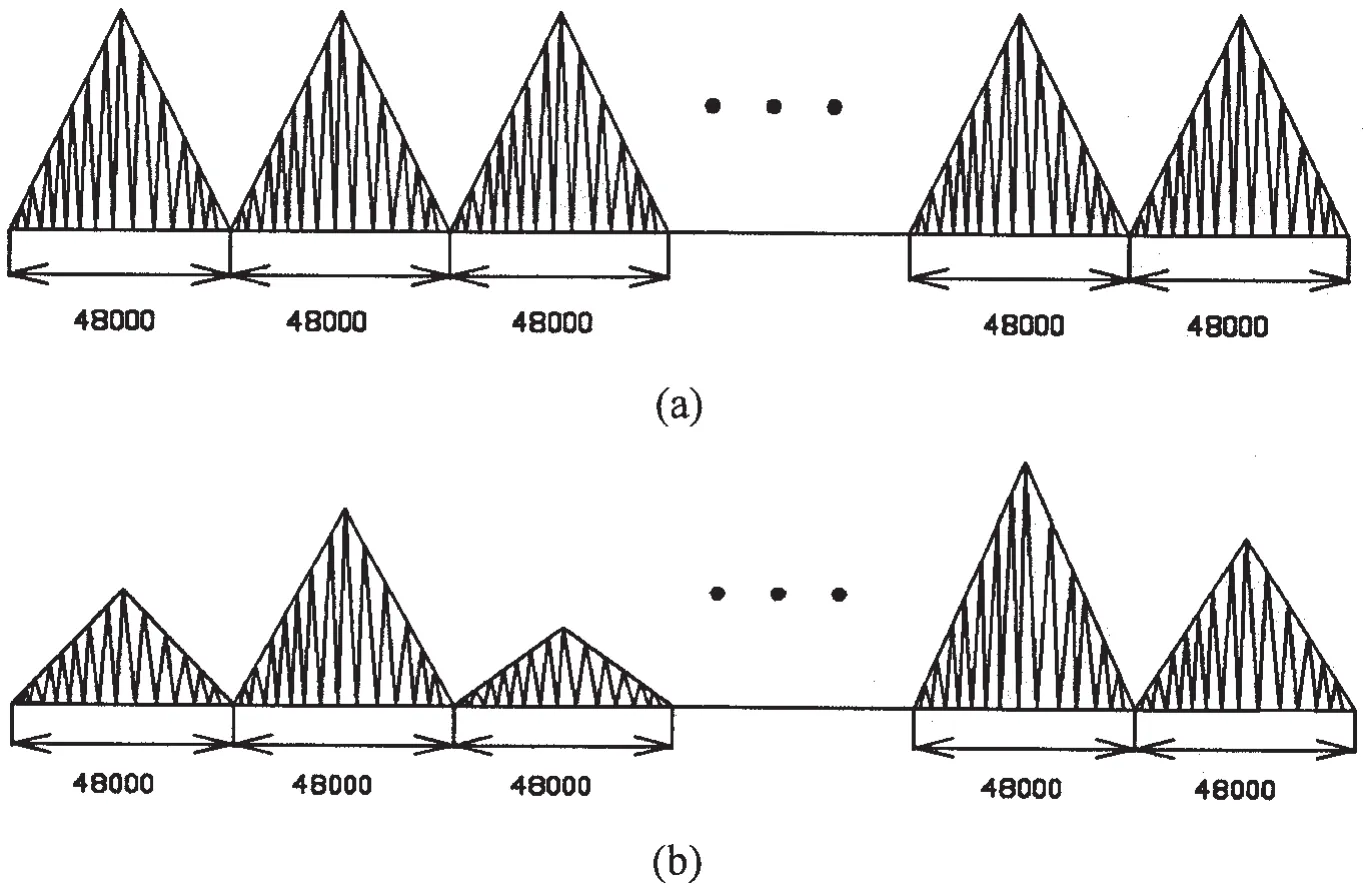
图6 风暴组合示意图Fig.6 Schematic diagram of storm group

为了分析连续风暴情况下对接接头焊缝焊趾处表面裂纹的疲劳裂纹扩展情况，本文选取了四种典型风暴组合。其中，Model 1表示风暴类型相同，Model 2表示风暴等级越来越高，Model 3表示风暴等级越来越低，Model 4表示风暴随机排列。图6为风暴组合示意图，其中：（a）表示风暴组合由相同等级的风暴组成；（b）表示风暴组合由不同等级的风暴组成。具体情况为：

（1）Storm Model 1：Storm C—Storm C—Storm C—Storm C—Storm C

（2）Storm Model 2：Storm A—Storm B—Storm C—Storm D—Storm E

（3）Storm Model 3：Storm E—Storm D—Storm C—Storm B—Storm A

（4）Storm Model 4：Storm A—Storm C—Storm E—Storm B—Storm D

对于初始裂纹的状态，由一般工业上无损探伤可以检测到的裂纹的大小或允许最大的缺陷尺寸的大者作为初始裂纹的尺寸：a0＞0.05 mm，c0＞0.5 mm，且由于焊趾表面裂纹多为同时多处萌生，初始裂纹长度c0应该取得较长。本文选取的初始裂纹长度c0=5 mm，初始裂纹深度a0分别取0.6 mm、0.8 mm和1 mm。四种风暴组合的循环次数均为2.4×105次。在这四种情况下，Model 2、Model 3和Model 4包含相同的风暴等级类型，但是由于风暴排列顺序不同，其对应的最终裂纹长度和深度均不相同，且在Model 2情况下最终裂纹长度和深度均最大，如图7-9所示。原因可以归结为：在Model 2情况下，风暴等级越来越高，载荷越来越大，故裂纹扩展速率越来越大。在Model 1、Model 2和Model 4情况下，当循环次数达到一个较大的值时，裂纹长度才开始变化。而在Model 3情况下，裂纹长度在最初阶段即开始变长。相对于其它三种风暴组合，Model 3情况下开始阶段的风暴等级最高，载荷较大，故裂纹增长速度较快。结果表明风暴的大小、顺序对裂纹扩展行为有明显的影响。

从图7-9可以看到，初始裂纹深度a0的取值越大，Model 4对应的最终裂纹深度和长度与Model 1情况下对应的值越接近。同时，在上述四种风暴组合下，如图10所示，均有a0/c0=0.20时对应的最终裂纹长度最长，a0/c0=0.16时次之，a0/c0=0.12时长度最短。原因为：由于以上情况选取的初始裂纹长度c0相同，当初始裂纹深度a0的取值较大时，由上文裂纹扩展率公式可知，裂纹长度和深度方向的扩展速率均较大，故当循环次数相同时，a0越大，最终裂纹长度越长。初始裂纹的尺寸大小对裂纹扩展影响显著，可见合理地确定初始裂纹尺寸是分析裂纹扩展非常关键的一步。

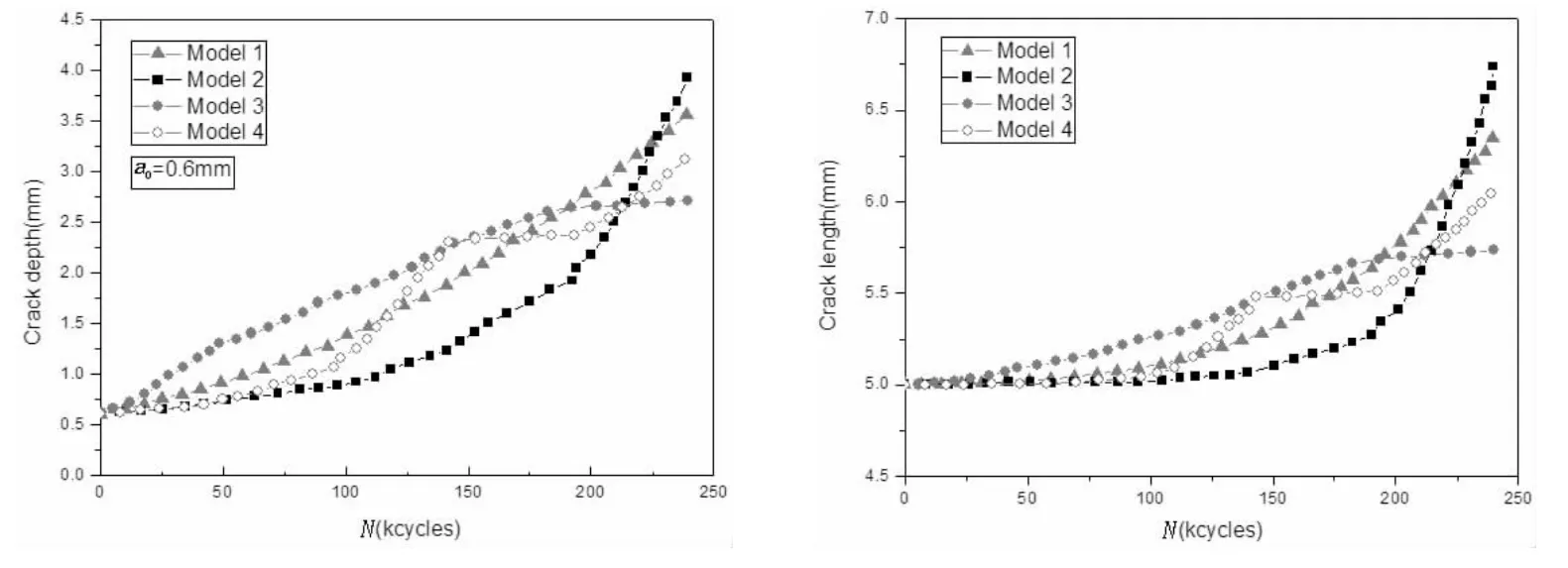
图7 裂纹大小随循环次数的变化（a0=0.6 mm，c0=5 mm）Fig.7 Variation of crack size during cycles

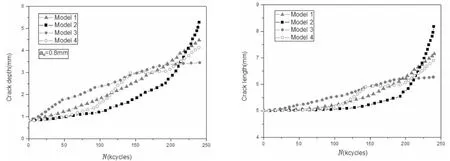
图8 裂纹大小随循环次数的变化（a0=0.8 mm，c0=5 mm）Fig.8 Variation of crack size during cycles

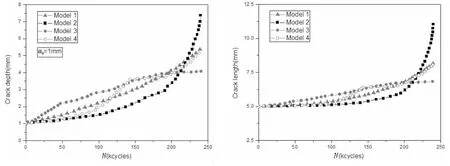
图9 裂纹大小随循环次数的变化（a0=1 mm，c0=5 mm）Fig.9 Variation of crack size during cycles

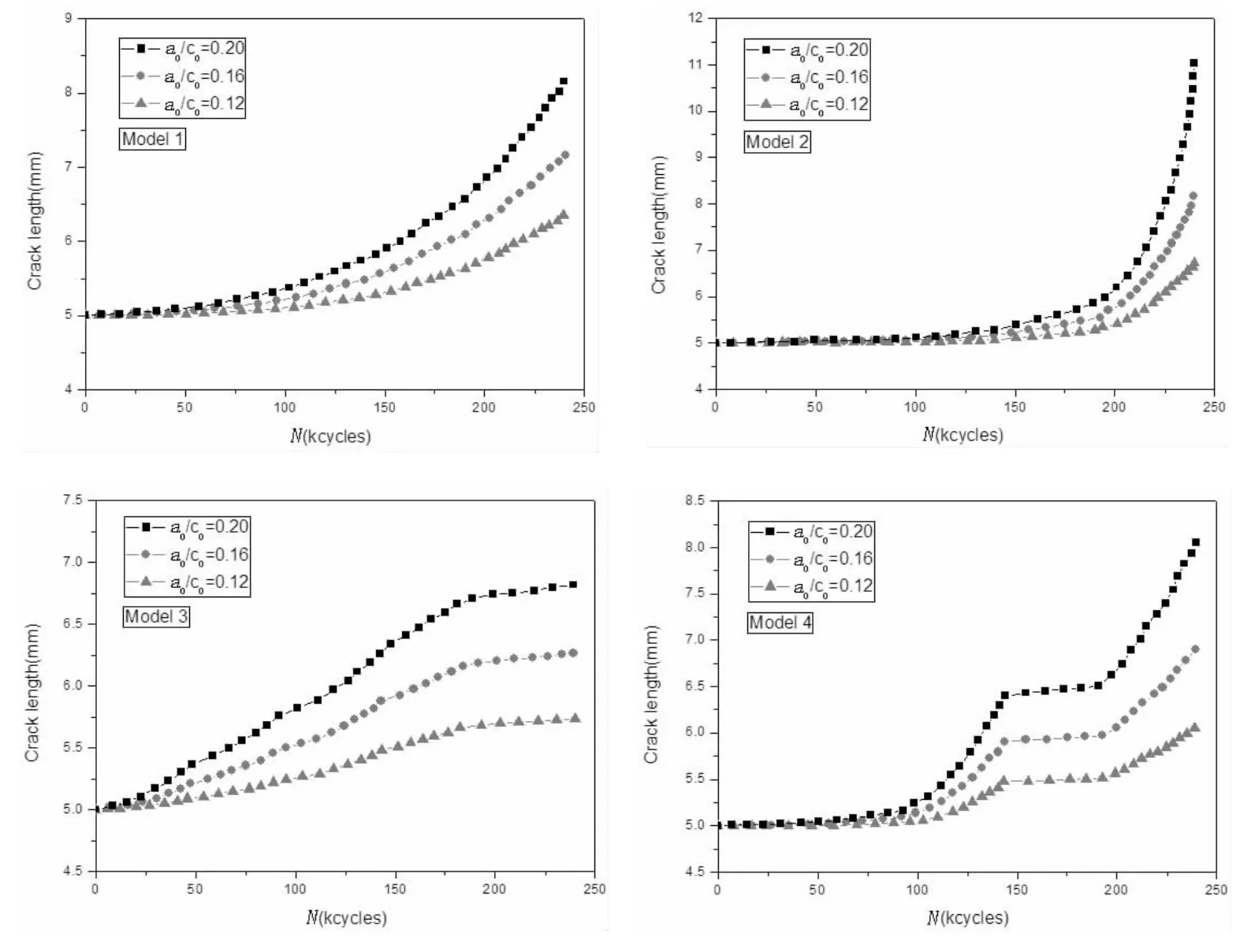
图10 在不同a0/c0情况下裂纹长度随循环次数的变化对比Fig.10 Comparison of variation of crack length during cycles under different ratios of a0/c0

从图7-10中可以看到，在Model 4情况下，裂纹深度方向和长度方向的扩展曲线均出现了很明显的裂纹迟滞现象。由于Model 4情况下最中间的风暴Storm E比第二个风暴Storm C高两个等级，比第四个风暴Storm B高三个等级，因此遭遇到Storm E时，会发生明显的过载。同时，如图11所示，当风暴类型、初始裂纹尺寸等均相同时，考虑残余应力影响时的裂纹扩展速率比不考虑残余应力时要大，残余应力对疲劳裂纹扩展行为的影响很明显。原因为：由于本文考虑的残余应力K（σR）＞0，此时载荷比R＞-1，而未考虑残余应力时，应力比R=-1，故由上文裂纹扩展率公式可知，考虑残余应力时的裂纹扩展速率较大。因此预报船舶结构的疲劳寿命时，应考虑残余应力的影响。

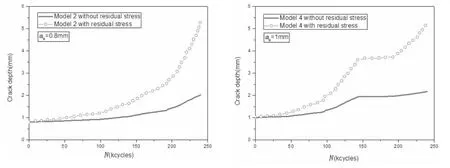
图11 残余应力对疲劳寿命的影响Fig.11 Effect of residual stress on fatigue life

4 结论

本文介绍了风暴模型及波浪诱导应力短期分布的基本特征，同时将风暴模型和裂纹扩展率单一曲线模型，焊趾表面裂纹应力强度因子计算方法以及残余应力引起的应力强度因子的计算方法结合起来，预报了对接焊接接头焊趾在几种典型风暴组合下的疲劳扩展行为，得到了以下结论：

（1）疲劳裂纹扩展预报方法中考虑了残余应力，焊趾放大系数，过载效应，应力比和门槛值等因素的影响，结合以风暴模型表示的随机波浪载荷，能有效预报船舶结构在复杂载荷作用下的疲劳裂纹扩展行为。

（2）船舶结构在连续风暴海况下的疲劳裂纹扩展预报结果表明，风暴的大小、顺序对裂纹扩展行为影响较大。

（3）船舶疲劳裂纹扩展寿命分析中确定合理的初始裂纹尺寸非常重要。

（4）船舶结构在两种情况下（即考虑残余应力影响和不考虑残余应力影响）的疲劳寿命预报结果表明，残余应力对疲劳寿命的影响很明显，因此预报船舶结构的疲劳寿命时，应考虑残余应力的影响。

本文使用的风暴模型是在连续风暴海况下，而实际上风暴模型是由平静海况和风暴海况随机交替组合的。为了更加真实地模拟实际海况，需要得到平静海况的平均浪高，平均持续时间等相关信息。同时本文将应力响应传递函数假定为常数，而实际上应力响应传递函数与波浪频率有关，随着频率的变化而变化，因此在这些方面有待于进一步研究和探讨。

[1]DNV.Fatigue assessment of ship structures[Z].HØvik:Det Norske Veritas Classification Notes No.30.7,January 2001.

[2]ABS.Rules for building and classing steel vessels[S].Houston:American Bureau of Shipping,2002.

[3]中国船级社.船体结构疲劳强度指南[M].北京:人民交通出版社,2001.

[4]冯国庆.船舶结构疲劳强度评估方法研究[D].哈尔滨:哈尔滨工程大学,2006.

[5]Lin N K,Hartt W H.Time series simulations of wide-band spectra for fatigue tests of offshore structures[J].Journal of Energy Resources Technology,1984,106(11):466-472.

[6]Tomita Y,Kawabe H,Fukuoka T.Statistical characteristics of wave-induced load and simulation method of wave loading pattern for fatigue desig[C]//Proceedings of the Third International Offshore and Polar Engineering Conference Stavanger, June 6-11,1993.Singapore,1993.

[7]Tomita Y,Matoba M,Kawabe H.Fatigue crack growth behavior under random loading model simulating real encountered wave condition[J].Marine Structures,1995,8:407-422.

[8]Terai K,Tomita Y,Hashimoto K,Osawa N.Fatigue design methold of ship structural members based on fatigue crack growth analysis[C]//Proceedings of the Eleventh International Offshore and Polar Engineering Conference Stavanger,June 17-22,2001.Norway,2001.

[9]Huang X P,Moan T.Improved modeling of the effect of R-ratio on crack growth rate[J].Int.J Fatigue,2007,29:591-602.

[10]Huang X P.Fatigue crack growth rate recommended in BS7910 and an unique crack growth rate curve under different load ratios[C]//ASME PVP 2007/CREEP 8 Conference,July 22-26,2007.San Antonio,Texas,USA,2007.

[11]Huang X P,Moan T,Cui W C.An engineering model of fatigue crack growth under variable ampiltude loading[J].Int.J Fatigue,2008,30:2-10.

[12]Huang X P,Moan T,Cui W C.A unique crack growth rate curve method for fatigue life prediction of steel structures[J]. Ships and Offshore Structures,2009,4(2):165-73.

[13]黄小平,韩芸,崔维成等.变幅载荷作用下焊接接头疲劳寿命预测方法[J].船舶力学,2005,9(1):89-97. Huang Xiaoping,Han Yun,Cui Weicheng,et al.Fatigue life prediction of weld-joint under variable amplitude fatigue load[J].Journal of Ship Mechanics,2005,9(1):89-97.

[14]BS7910.Guide on methods for assessing the acceptability of flaws in structures[M].British Standard Institution,1999.

[15]张毅,黄小平,崔维成,卞如冈等.对接接头焊趾应力集中有限元分析[J].船舶力学,2004,8(5):91-99. Zhang Yi,Huang Xiaoping,Cui Weicheng,et al.Finite element analysis on stress concentration at weld toe of butt-welded joints[J].Journal of Ship Mechanics,2004,8(5):91-99.

[16]Miki C,Mori T,Desvigns M,et al.Effect of stress ration and tensile residual stress on near threshold fatigue crack growth [J].Structure Engineering and Earthquake Engineering,1986,3(1):175-182.

[17]Bueckner H F.A novel principle for the computation of stress intensity factors[J].ZAMM,1970,50:529-546.

[18]Rice R J.Some remarks on elastic crack-tip stress fields[J].Int.J Solids Structure,1972,8:751-758.

[19]Wang X,Lambert S B.Stress intensity factors for low aspect ratio semi-elliptical surface cracks in finite-thickness plates subjected to nonuniform stresses[J].Engineering Fracture Mechanics,1995,51(4):517-532.

[20]Shiratori M,Miyoshi T,Tanikawa K.Analysis of stress intensity factors for surface cracks subjected to arbitrarily distributed surface stresses,in Stress Intensity Factors Handbook(Editor-in-Chief Murakami Y)[M].Oxford:Pergamon Press,1987,2:725-727.

[21]Brown W F,Srawley J E.Plane strain crack toughness testing of high strength metallic material[Z].ASTM STP 410, 1966.

[22]Gross B,Srawley J E.Stress intensity factor for single-edge-notch specimens in bending or combined bending and tension by boundary collocation of a stress function[Z].NASA TN,D-2603,1965.

A procedure to predict fatigue crack growth of ship structures under complex loading condition

ZHANG Ding1,HUANG Xiao-ping2,CUI Wei-cheng3
(1.Marine Design&Research Institute of China,Shanghai 200011,China;2.State Key Lab of Ocean Engineering, Shanghai Jiao Tong University,Shanghai 200240,China;3.Hadal Science and Technology Research Center,Shanghai Ocean University,Shanghai 201306,China)

Storm model proposed by Tomita and coworkers is a simplified random loading model for fatigue strength assessment of ship structures.The time dependent random wave loading can be expressed by the storm model.The basic characteristics of storm model and short-term distribution situation of wave-induced stress are described.Storm model is combined with a unique crack growth rate curve and SIF calculation equations for surface crack in the weld toe,and the procedure to predict the fatigue crack growth behavior of ship structures under complex loading conditions is discussed.Weight function is used to calculate SIF of surface crack under given residual stress distribution.Fatigue crack growth behavior of surface crack at weld toe of butt welded joint in ship hull under storm wave loading condition is predicted.The results show that the size and order of storms,the initial size of crack and residual stress have significant effect oncrack growth behavior.Reasonable storm model parameters and initial crack size are very important for fatigue life prediction of ship structures.

storm model;wave-induced stress;unique curve model;residual stress;surface crack; fatigue crack growth predication

U661.4

A

10.3969/j.issn.1007-7294.2015.05.009

1007-7294（2015）05-0541-12

2014-05-15

上海市自然基金项目（08ZZR1410000）；江苏省创新学者基金项目（BK2008004）资助项目

张鼎（1986-），男，硕士，E-mail：zhangding@stju.edu.cn；

黄小平（1964-），男，副教授，E-mail：xphuang@stju.edu.cn。