计入船体变形激励的大型船舶推进轴系振动性能研究
田哲,张聪,严新平,熊冶平
(1武汉理工大学,武汉430063;2船舶动力工程技术交通行业重点实验室,武汉430063;3国家水运安全工程技术研究中心,武汉430063;4南安普顿大学,南安普顿SO16 7QF)
计入船体变形激励的大型船舶推进轴系振动性能研究
田哲1,2,3,4,张聪1,2,3,严新平1,2,3,熊冶平1,4
(1武汉理工大学,武汉430063;2船舶动力工程技术交通行业重点实验室,武汉430063;3国家水运安全工程技术研究中心,武汉430063;4南安普顿大学,南安普顿SO16 7QF)
大型船舶的船体变形与其推进系统之间的耦合影响成为船舶领域的研究热点,开展船体变形激励下的推进轴系振动性能的研究对保证船舶可靠运行十分必要。文章以船舶轴系动力学方程为研究基础,建立其计入船体变形激励的大型船舶推进轴系的动力学模型并通过解析解与数值解的对比验证了方法的可靠性。依据此模型,以某大型集装箱船舶为研究对象,分别探索了船体变形激励不确定方向下以及变尺寸参数下轴系振动的影响规律,为大型船舶船体变形激励下的轴系振动问题提供了理论基础。
船体变形;轴系;不确定性;变参数;振动特性
0 引言
船舶是实施航运与海洋开发战略的重要载体,是保障我国海洋权益和海洋资源安全的有效装备。船舶轴系是船舶动力系统的重要组成部分,承担了将船舶主机动力传递到螺旋桨、产生推力实现船舶推进的重要功能。随着船舶大型化趋势的出现,船体主参数明显增大,船舶轴系的输出功率、传递推力、结构尺度等参数不断增大。由于船体在不同工况下与波浪相互作用发生剧烈的动态变形,变形激励通过船体—轴承—轴系传递作用于推进轴系,引起轴系振动加剧,当船舶推进系统的振动超过允许的幅值时,极易引起推进系统故障,威胁船舶运行安全。由于船体的板壳结构与轴承基座相比,相对柔软,轴系振动激励也会通过轴系—轴承—船体传递作用于船体[1]。激励极易引起船体尾部强烈振动,影响船舶疲劳寿命[2]。
在水环境中,大型船舶的船体变形与其推进系统之间的耦合影响已成为船舶领域的研究热点,引起世界上相关的专家学者及各国船级社的高度重视。日本船级社ClassNK较早地开展了将船体变形纳入船舶轴系计算校核的研究并提出了Prime Ship计划[3],来研究船体变形下轴系校中、轴系扭振和船舶运行状态评估。美国船级社ABS开发出一套新的考虑船体影响的ABS SHAFT轴系校中分析系统[4]。中国船级社CCS近些年才将船体变形因素对轴系的影响纳入COMPASS轴系计算软件系统[5]。王宏志等人[6]针对船体变形对轴系状态的影响,从中间轴承入手研究不同位置情况下轴系布置以适应船体的变形。周春良等人[7]运用Ansys软件的谱分析法分析了船体激振下轴系振动响应。宋希庚等人[8]利用有限元仿真分析出船体变形并通过拟合曲线的形式求解轴承变位进行了轴系校中研究。耿厚才等人[9]通过有限元模拟来研究考虑船体变形下的中间轴承布置方案。Murawski[10]运用有限元软件Nastran考虑了船体柔性结构和变形的轴系校中做了相关的仿真研究。Roemen和Grevink[11]用有限元建立了一个包含轴承的轴系模型来分析一种规避轴系共振的方法。从上述可以看出运用有限元软件仿真的方法是研究船体变形对船舶轴系影响一种普遍适用的手段,并且考虑船体变形的影响的研究多集中在轴系校中方向,在轴系振动方向还鲜有报道。故本研究从船舶轴系运动方程出发,在理论层面建立轴系动力学模型,通过计入船体变形激励的形式研究轴系振动情况,以某大型集装箱船舶为算例,结合一海况下的船体变形激励来求解轴系的振动响应。
1 推进系统模型
为分析问题的方便,取推进轴系的中间轴、尾轴及多个中间弹性支承轴承的二维简化模型来分析船体变形下轴系振动情况。如图1受力图所示,波浪载荷作用于船体上,引起船体的变形,在轴承弹性支撑轴承处承受船体变形力,传递到轴系,引起轴系振动。

图1 船体变形作用下的船舶推进轴系分析模型Fig.1 The analysis model of propulsion under the hull deformation load
1.1 推进轴系理论建模
在图1所示的坐标系x-o-y中,假如某船舶拥有n个弹性支承轴承,其位置分别为B1,B2,…,Bn,其轴承的刚度分别为K1,K2,…,Kn,则n个支撑轴承将长度为L的轴系分成跨度分别为L1,L2,...,Ln+1的n+1段。船舶轴系在简化理论模型中为均质梁,各段的横截面积为Si,及各段质量密度为ρi。将轴系各段的位移用Ui(x,t)表示,其中Bi-1<x<Bi,i=1,2,…,n+1(i表示第i段轴)。不考虑轴承与轴系之间油膜力及轴承本身阻尼的非线性作用,运用Euler-Bernoulli梁理论,各轴段的振动方程为[12]:

式中:EiIi为第i轴段的弯曲刚度,t为时间。
利用分离变量法易知该振动方程的解的一种形式为:

式中:Zi(t)为各轴段的广义坐标,Φi(x)为各轴段的模态函数。
由此可知,各轴段的振动形式是幅值按Zi(t)随时间变化、按指定形状Φi(x)进行的运动。用撇表示对x的导数,用圆点表示对t的导数,利用(2)式代入(1)式可导出



式中:Ai,Bi,Ci,Di为第i轴段的实常数。
1.2 连续条件和边界条件
在自由振动条件下,因为有多个支承轴承的存在,故每一段的轴在弹性支承轴承处位移、斜率、弯矩和剪力的连续条件分别为:
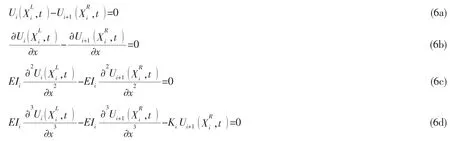
推进轴系取中间轴及尾轴,暂不考虑螺旋桨、法兰盘及主机端的影响,故推进轴系以自由—自由梁的形式出现在模型中。自由—自由梁两端的边界条件如下所示:

以某大型集装箱船舶推进轴系为例验证模型。推进轴共含有四个支承轴承,因支承轴承都安装在中间轴承及尾轴上,故为方便描述,以中间轴承为临界点将轴系从尾轴端至主机端重新划分为L1、L2、L3、L4和L5五段。推进轴系及轴承参数如表1所示。

表1 推进轴系及轴承参数Tab.1 Parameters of the shaft and bearings
轴系各段的弹性模量均为Ei=2.11×1011Pa/m2,惯性矩将(5)式代入(6a)、(6b)、(6c)、(6d)、(7)式和(8)式得出等式,连立可得如公式(9)所示的矩阵形式。


将表1中的推进轴系与轴承数据代入对应矩阵项,得到该集箱船舶推进轴系的固有频率的解析解,将其与Ansys建模得到的数值解对比如图2所示。从图中可以看出,解析解与数值解结果基本一致。由此可利用已建立的模型来模拟船体变形激励情况下的轴系振动分析。

图2 加入支承轴承的轴系自由振动固有频率解析解与数值解的比较Fig.2 Comparison of the analytical and numerical results for shaft’s free frequencies adding supports
1.3 计入船体变形激励的理论模型
由图1的受力图可知,船体变形激励分别作用于各个轴承位置处,在此引入狄拉克δ函数,来表示在第i个轴承处的受到的船体变形的激励力为

引入船体变形激励力以后,连续条件中的方程(6d)则变为

2 算例分析
以表1所示某大型集装箱船舶为例,在波长319.98 m,波向180°,波高10 m时,四个轴承B1-B4所受船体激励幅值分别为:548 170 N,1 375 600 N,1 187 400 N,1 634 900 N,方向均向下。取频率范围1-60 Hz,频率间隔1 Hz,位移参考值为1e-12 m),则主机端的振动响应如图3所示,尾轴端的振动响应如图4所示。从图中可以看出解析法与数值法计算的船体激励下轴系响应位移曲线趋势一致,波峰位置相同,峰值大小虽然有一定偏差,这主要是由于取值精度导致的。总体来说,偏差范围不大,两条曲线吻合情况较好。由此可以得出,本文中采用的计算船体在轴承处激励作用下轴系位移响应的方法是正确有效的。

图3 主机端振动响应Fig.3 The response of vibration on the main engine end

图4 尾轴端振动响应Fig.4 The response of vibration on the stern shaft end
2.1 不同船体变形激励方向对轴系振动响应的影响
因波浪引起的船体变形具有不确定性,本部分着重研究了船体变形激励力在施加方向上的不确定性。依次单独改变B1、B2、B3和B4支承轴承处船体激励力的方向,使之向上,其它支承轴承处船体激励力方向保持向下,则由此得到四组轴系振动响应数据,与初始模型轴承处船体激励力均向下,即图3所示的主机端振动响应和图4所示的尾轴端振动响应为参考值做对比,得到不同激励方向下两端的响应曲线如图5和图6所示。

图5 主机端不同船体变形激励方向下的轴系振动响应Fig.5 The response of shaft vibration in different direction of ship hull deformations(The main engine end)
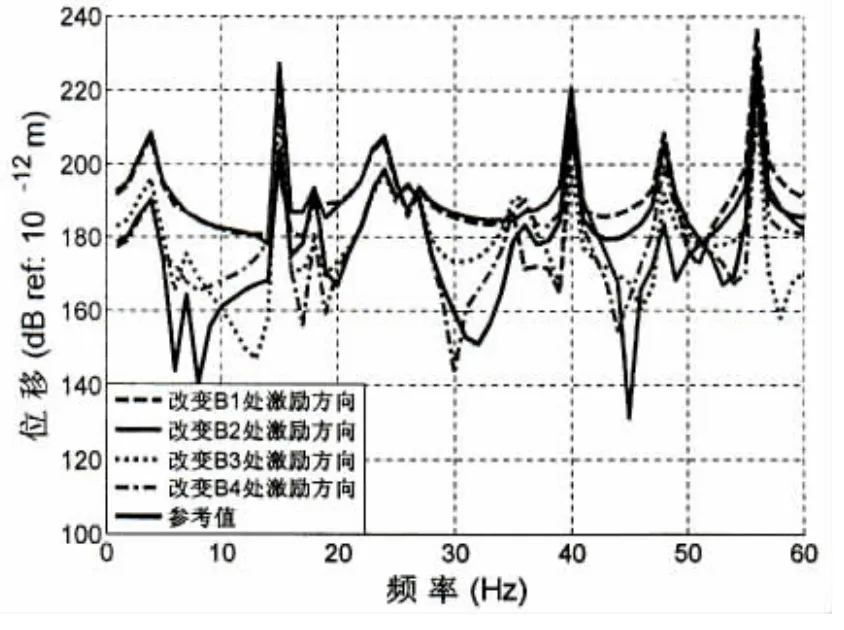
图6 尾轴端不同船体变形激励方向下的轴系振动响应Fig.6 The response of shaft vibration in different direction of ship hull deformations(The stern shaft end)
从图中可以看出,船体变形激励力的方向对推进轴系的振动幅值影响明显。改变激励力方向的振动比参考值的振动从波峰到波谷的振动衰减率明显增大,说明混合振动方向下的振动持续时间长,对推进轴系的危害更大。
2.2 船体变形激励对不同尺寸的轴系振动响应影响
以上文所述的某大型船舶推进轴系模型为初始模型。引入参数η=L1/L来表征推进轴系的长度比,λ=D1/D来表征推进轴系的直径比,ε=η/λ来表征推进轴系的自身的尺寸比。以上文所述的某大型船舶推进轴系模型为初始模型即η=1,λ=1,ε=1。图7为在直径相同的情况下,不同长度推进轴系受到相同船体变形激励下的主机端轴系振动响应情况。图中1、2、3、4点分别是不同长度推进轴系的一阶共振点,据此分析得到轴系越长,在低频下越容易引起轴系的振动,所以长轴系船舶要注意低频范围内振动损害。

图7 相同直径、不同长度下推进轴系受到相同船体变形激励下的振动响应Fig.7 The response of vibration for different lengths of shafts excited by the same hull deformations
图8为长度相同的情况下,不同直径的推进轴系受到相同船体变形激励下的主机端轴系振动响应情况。图中1、2、3、4点分别是不同直径的推进轴系的一阶共振点,通过不同λ下的波峰比较分析得出轴系直径越小,共振频率越低,并且振动幅值相对较大。

图8 相同长度、不同直径下推进轴系受到相同船体变形激励下的振动响应Fig.8 The response of vibration for different diameters of shafts excited by the same hull deformations
当同时改变η、λ值,并保证ε保持不变的情况下,在相同船体变形激励下的轴系振动情况如图9所示。运用前文所述船体激励,改变其大小,轴系其他参数保持不变,轴系振动情况如图10所示。
由图9曲线结果可以看出,虽然ε保持不变,但是同时改变η、λ,振动曲线形状和波峰位置均发生了较大改变。由图10曲线结果可知,船体变形激励力大小仅仅影响的是轴系的幅值,而对轴系振动频率、振动衰减率没有影响。由此可知推进轴系振动分析的一般性规律,大型船舶推进轴系越粗长更易发生低频振动,并且振动持续时间也越长,同时,随着激振幅值增大,其振动幅值也将增大,当长时间运行在低频共振频率附近时,其振动损害将严重影响运行可靠性。在分析船体激励下轴系响应的问题上,相似性原理并不适用。

图9 按比例缩放的推进轴系受到相同船体变形激励下的振动响应Fig.9 The response of vibration for scale shafts excited by the same hull deformations

图10 不同船体激励大小下轴系振动响应Fig.10 The response of shaft vibration under different kinds of hull deformations
3 结论
本文基于船舶轴系动力学方程,建立了计入船体变形激励的推进轴系振动模型,其中船体变形激励视作加载在支承轴承处的外部载荷,通过改变轴承处的连续条件实现。文中将该解析法计算所得的船舶轴系自由振动结果及某一海况下船体变形激励下的轴系振动响应结果分别与数值法计算结果进行了对比,验证了该方法的正确性。以此为基础,讨论了不确定性引起的不同方向船体变形激励对轴系振动影响及船体变形激励对不同轴系尺寸的推进轴系振动响应影响,得到了以下结论:
(1)船体变形激励方向的不确定性会引起轴系振动幅值、频率和衰减时间的变化。对比单一方向的船体变形激励,混合方向的船体变形激励下的振动持续时间更长,对推进轴系的危害更大。
(2)船舶轴系尺寸参数对轴系振动有一定影响。直径相同时,长度越长的轴系更易发生低频振动,而长度相同时,直径越细的轴系更易发生低频振动。
(3)船体变形激励力大小仅仅影响的是轴系的幅值,而对轴系振动频率、振动衰减率没有影响。因此在分析船体激励下轴系响应的问题上,相似性原理并不适用。
[1]严新平,李志雄,刘正林,杨平,朱汉华,杨忠民.大型船舶推进系统与船体耦合动力学研究综述[J].船舶力学, 2013,17(4):439-449. Yan Xinping,Li Zhixiong,Liu Zhenglin,Yang Ping,Zhu Hanhua,Yang Zhongmin.Study on coupling dynamical theory for interaction of propulsion system and hull of large ships:a review[J].Journal of Ship Mechanics,2013,17(4):439-449.
[2]吴晞,韩晓光,李宇辰.水深对船舶摇荡运动影响的数值方法研究[J].交通信息与安全,2013,31(4):4 5-48. Wu Xi,Han Xiaoguang,Li Chenyu.Numerical methods for impact of water depth on ship swaying motions[J].Journal of Transport Information,2013,31(4):45-48.
[3]CLASS NK-PrimeShip[OL].http://www.classnk.or.jp/hp/en/activities/primeship/index.html.
[4]Editorial of MER.An aligned view on shafts[J].MER-Marine Engineers Review,2006(5):44-47.
[5]董恒健,张建军.对轴系校中影响的船体变形研究[J].船舶工程,2009,31(5):8-11. Dong Hengjian,Zhang Jianjun.Study on the hull deflection for the effect of shafting alignment[J].Ship Engineering,2009, 31(5):8-11.
[6]王宏志,魏海军,关德林,陈椿芳.中间轴承对船舶轴系力学状态影响的数字模拟[J].船舶力学,2006,10(1):98-105. Wang Hongzhi,Wei Haijun,Guang Delin,Chen Chunfang.Numerical simulation on ship shafting mechanics condition of intermediate bearing[J].Journal of Ship Mechanics,2006,10(1):98-105.
[7]周春良.船舶轴系振动研究[D].哈尔滨:哈尔滨工程大学,2006. Zhou Chunliang.Vibration research on ship shafting system[D].Harbin:Harbin Engineering University,2006
[8]石磊,薛冬新,宋希庚.计入船体变形影响的轴系动态校中研究[J].大连理工大学学报,2011,51(3):375-380. Shi Lei,Xue Dongxin,Song Xigeng.Study of dynamic shafting alignment considering ship hull deformations[J].Journal of Dalian University of Technology,2011,51(3):375-380
[9]耿厚才,郑双燕,陈建.大型船舶船体变形对轴系校中的影响分析[J].船舶工程,2010,32(5):7-9. Geng Houcai,Zheng Shuangyan,Chen Jian.Influence analysis of large vessel hull deformation on shafting alignment[J]. Ship Engineering,2010,32(5):7-9
[10]Murawski L.Shaft line alignment analysis taking ship construction flexibility and deformations into consideration[J].Marine Structures,2005,18:62-84.
[11]Roemen R,Grevink J.An advanced approach to the design of shaftlines and bearing arrangements for fast ferries[J].Wartsilia Technical Journal,2009,1:47-53.
[12]Clough R,Penzien J.Dynamics of structures.Computers&Structures[M].Inc,University Ave.Berkeley,USA,2005.
Vibration characteristic study of large vessel’s shaft system taking into account the ship hull deformation excitations
TIAN Zhe1,2,3,4,ZHANG Cong1,2,3,YAN Xin-ping1,2,3,XIONG Ye-ping1,4
(1.Wuhan University of Technology,Wuhan 430063,China;2.Key Laboratory of Marine Power Engineering&Technology (Ministry of Communications),Wuhan 430063,China;3.National Engineering Research Center for Water Transport Safety, Wuhan 430063,China;4.University of Southampton,Southampton,Boldrewood Campus,SO16 7QF,United Kingdom)
As the effect on the interaction between the large vessel’s hull deformation and propulsion system becomes a research hotspot,it is necessary to research the vibration characteristics of the shaft excited by the ship hull deformation to guarantee the reliable operation in the sea.Based on the dynamic equations, this paper aims to establish the dynamic model of the propulsion shaft taking into account the ship hull deformation excitations.The analytical results of the model are compared with the numerical results to confirm that the model is reliable.Based on one typical large container vessel,the shaft vibration characteristics are studied under ship hull deformation excitations with different directions and parameters respectively. Groundwork is made for further research in shaft vibration problem considering ship hull deformation.
ship hull deformation;shaft;uncertainty;variable parameter;vibration characteristics
U661.44
A
10.3969/j.issn.1007-7294.2015.11.010
1007-7294(2015)11-1368-09
2015-06-24
国家自然科学基金重点项目(No.51139005);中央高校基本科研业务费专项资金(2014-JL-006)
田哲(1988-),男,博士生;
张聪(1986-),女,讲师,E-mail:zhangcong@whut.edu.cn。

