深水耐压壳仿生设计与分析

张建，王纬波，高杰，王明禄，唐文献，吴文伟

（1中国船舶科学研究中心，江苏无锡214082；2江苏科技大学，江苏镇江212003）

深水耐压壳仿生设计与分析

张建1，2，王纬波1，高杰2，王明禄2，唐文献2，吴文伟1

（1中国船舶科学研究中心，江苏无锡214082；2江苏科技大学，江苏镇江212003）

文章研究了千米水深蛋壳仿生耐压壳的设计理论与分析方法，首先采用Upadhyaya方程、N-R方程，分别建立了鸡蛋壳、鹅蛋壳形状函数；其次，设计了6 km水深鸡蛋壳、鹅蛋壳仿生耐压壳，并基于解析法和数值法，对这两种结构进行强度和稳定性研究；最后，建立了球形、抛物线形、柱形、椭球形等4种典型耐压壳的数值模型，与仿生耐压壳作对比分析。结果表明：解析法和数值法所得的经向应力、纬向应力、临界屈曲应力吻合良好，鹅蛋壳仿生耐压壳的强度和稳定性优于鸡蛋壳仿生耐压壳，具有较好的耐压特性；球形耐压壳储备浮力能力最优，鹅蛋形、鸡蛋形、柱形、椭球形、抛物线形耐压壳的储备浮力能力分别是球的87%、82%、68%、67%、66%；从储备浮力、壳内空间利用率、流线型、乘员舒适性等方面综合比较可知，鹅蛋壳仿生耐压壳可为深水耐压壳设计提供有效参考。

深水耐压壳；鸡蛋壳；鹅蛋壳；仿生设计

Key words:deepwater pressure hull;chicken eggshell;goose eggshell;bionic design

0 引言

人类开发海洋的速度不断加快，从近海到远海深度不断增加。各种作业目的的潜水器种类繁多，发展迅速，主要应用于石油勘探与开发、科学研究、矿物资源开采、军事探测和打捞等方面。作为潜水器浮力的主要提供者，耐压壳组成一个水密空间，保证在下潜过程中内部具有相对恒定的压力，耐压壳重量占潜水器总重量的1/4-1/2[1]。耐压设计需要考虑浮力系数（重量与排水量比值）、壳内空间利用率、水动力学特性、乘员舒适性等因素[2-3]。

现役耐压壳可分为球形结构、柱形结构以及椭球结构。其中，球形壳具有强度高、稳定性好、浮力系数低、材料利用率高等优点，但空间利用率低、水动力学特性差，在深水潜水器中广泛应用；柱形壳具有加工容易、空间利用率高、水动力学特性好等特点，但浮力系数大、材料利用率低、弯曲应力高，且需要内部加强，一般应用于潜水潜水器；椭球壳则是球形壳和柱形壳的折中方案。此外，耐压壳还包括具有良好水动力学特性的水滴结构，以及具有较强耐压特性的环形结构，但均严重牺牲了耐压壳的其它性能，没有得到广泛应用[4-8]。

自然界生物不断进化，壳类结构具有良好的耐压特性，满足生物生存需求，如蛋壳、头颅、贝壳、螺壳等。其中，蛋壳是一种满足正高斯曲线的多焦点、回转型薄壁结构，具有良好的重量/强度比、跨距/厚度比、美学特性以及合理的材料分布。蛋壳满足圆顶原理，无需额外加强支撑，利用最少材料就可以获得足够的强度和稳定性，是一种优异的仿生模型，建筑领域广泛采用蛋壳形仿生结构。在均布压力作用下，蛋壳可通过面内压力抵抗外载荷，此时壳体表现出超强的耐压特性。耐压壳是承受静水压力的薄壳结构，要求其具有良好的强度、稳定性、储备浮力能力、水动力学特性、壳内空间利用率以及乘员舒适性。显然，蛋壳可为深海耐压壳设计提供有效的生物信息[9-11]。

为此，本文根据鸡蛋壳、鹅蛋壳的生物学特性，建立其形状分布函数；以此为信息源，分别设计了鸡蛋壳、鹅蛋壳仿生耐压壳结构，并建立了这两种结构的解析模型和数值模型，研究其强度和稳定性；同时，建立了球形、椭球形、抛物线形、柱形等4种典型耐压壳的数值模型，与仿生耐压壳性能作对比分析。

1 蛋壳仿生耐压壳设计及解析模型推导

根据鸡蛋壳、鹅蛋壳的生物学特性，设计蛋壳仿生耐压壳结构，在此基础上，推导其强度和弹性屈曲方程。

1.1 仿生耐压壳设计

以鸡蛋蛋壳为生物原型，进行6 km水深耐压壳设计，根据CCS《潜水系统和潜水器入级与建造规范》，计算载荷取98 MPa。鸡蛋壳为轴对称旋转薄壳结构，子午面曲线方程采用Upadhyaya方程[12]表述（（1）式），该方程的系数由姜松、崔志平对300枚鸡蛋进行几何参数测试并取均值获取[13]，其中，长轴2a、短轴2b、蛋形角θ的均值分别为58.35 mm、43.74 mm、10°，蛋壳厚度t的均值为0.35 mm。根据鸡蛋的生物学信息，设计出的鸡蛋壳仿生耐压壳（图1），其截面参数为：长轴2.42 m、短轴1.84 m、蛋形角10°、厚度75 mm；材料选取钛合金Ti-6Al-4V（TC4），其力学参数为：弹性模量E=110 GPa，泊松比μ=0.3，屈服强度σy=830 MPa，密度ρ=4.5 g/cm3。

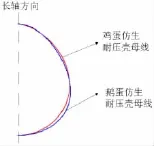
图1 2种蛋壳仿生耐压壳母线对比图Fig.1 Comparison between two bus lines of bionic pressure hulls

同理，以鹅蛋蛋壳为生物原型，进行6km水深耐压壳设计，计算载荷取98 MPa。鹅蛋壳也为轴对称旋转薄壳结构，子午面曲线方程采用N-R方程表述[14]（（2）式），设计出仿生耐压壳与鸡蛋壳仿生耐压壳体积相等，其截面参数为：长轴2.453 m、短轴1.836 m、厚度75 mm，材料仍然为钛合金Ti-6Al-4V（TC4），如图1所示。

1.2 仿生耐压壳强度及稳定性的解析模型

两种蛋壳仿生耐压壳均为轴对称薄壳结构，故采用薄壳理论[15]进行理论推导，首先推导鸡蛋壳仿生耐压壳的强度及稳定性方程（图2），由（1）式可得（3）式。

图2 鸡蛋壳子午线示意图Fig.2 Schematic of the chicken eggshell meridian

该曲线关于x轴对称，故取y为正，对其分别求一阶、二阶导函数：

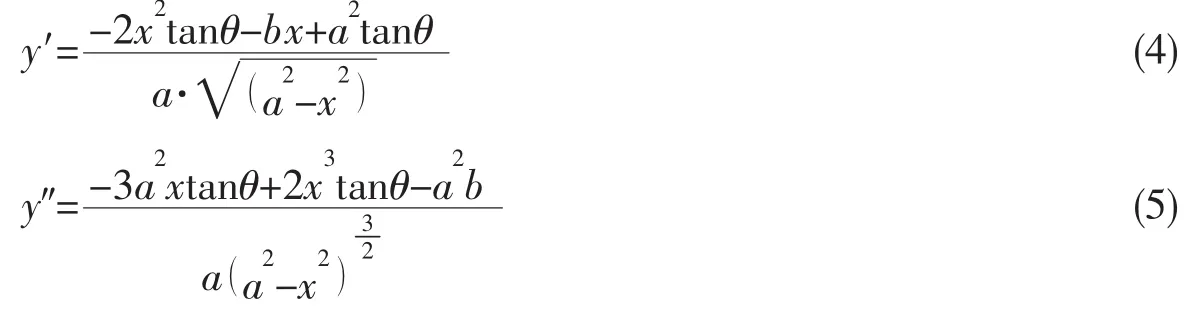
如图2所示，直角三角形MNP中存在如下三角函数关系：

由勾股定理可得第二曲率半径（（7）式），运用弧微分方程得第一曲率半径（（8）式）：

根据微体平衡方程，可以推得鸡蛋壳的经向应力δφ和纬向应力δθ：

其中：p为仿生耐压壳所受外压力，t为仿生耐压壳厚度。

鸡蛋壳仿生耐压壳的屈曲临界应力，采用Mushtri方程[16]求得：

其中：t为厚度，R1，R2为壳上主要曲率半径的平均值。

同理，可推导鹅蛋壳仿生耐压壳的经向应力和纬向应力及屈曲临界应力，对鹅蛋的方程（2）分别求y的一阶，二阶导函数：

其余计算过程与（6）式—（11）式相同。

2 耐压壳数值模型

2.1 蛋壳仿生耐压壳数值模型

采用pro/e软件，进行三维CAD建模，并抽取中面，采用ANSA前处理软件，进行网格划分，网格的划分形式参照的是网球画法，将壳体等分成6块，单元类型为线性四边形单元S4，鸡蛋壳仿生耐压壳共6 534个单元、7 866个节点；鹅蛋壳仿生耐压壳共6 654个单元、7 965个节点。计算载荷以均布压力形式施加在耐压壳表面；理论上是耐压壳不受任何约束，为了消除模型的刚性位移，选择三个点限制其六个方向位移。所求得各约束反力接近0，说明所施加的约束为虚约束，仅限制了模型的刚体位移。定义2种工况进行分析：（1）线性准静态分析；（2）线性屈曲分析。采用ABAQUS/Standard对该模型（图3）进行求解计算，最后，运用ABAQUS/Viewer进行后处理。

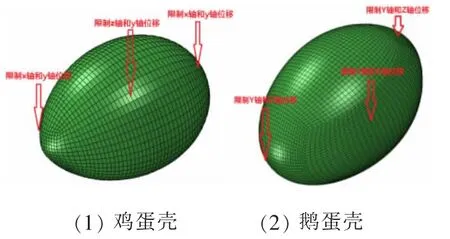
图3 仿生耐压壳数值模型Fig.3 Numerical models of bionic pressure hulls

2.2 4种典型耐压壳数值模型

为了验证蛋壳仿生耐压壳的有效性，参考CCS《潜水系统和潜水器入级与建造规范》规范和相关论文资料，分别设计了球形耐压壳[17]、抛物线性耐压壳[18]、椭球形耐压壳[18]、柱形耐压壳[19]等4种典型结构（图4、表2），其材料均为钛合金Ti-6Al-4V（TC4）。在设计过程中，满足如下条件：（1）耐压壳最大等效应力≤0.79σy；（2）弹性屈曲特征值≥3.00；（3）耐压壳内部体积为4.2 m3。在此基础上，分别建立了球形耐压壳、抛物线形耐压壳、椭球形耐压壳、柱形耐压壳的数值模型，如图4、表1所示，其离散思想、边界条件、载荷、分析工况、求解过程和结果分析方法均与蛋壳仿生耐压壳一致。

图4 4种典型耐压壳数值模型Fig.4 Numerical models of the four classical pressure hulls

表1 4种典型耐压壳结构及模型参数Tab.1 Structure and model parameters of the four classical pressure hulls

3 结果分析与讨论

由解析法和数值法，均可计算出鸡蛋壳仿生耐压壳的经向应力、纬向应力，在其危险区域依次取10个点进行比较分析，如图5（1）所示，可见，两种方法所得的纬向应力结果基本一样，经向应力结果具有良好的一致性，最大误差为3.2%，证明鸡蛋壳仿生耐压壳强度分析模型是正确的；由解析法计算所得的鸡蛋壳仿生耐压壳屈曲应力为357.00 MPa，数值法计算所得的屈曲应力为341.04 MPa，两者相差4.4%，证明鸡蛋壳仿生耐压壳屈曲分析模型是正确的。

两种方法计算所得的鹅蛋壳仿生耐压壳的经向应力、纬向应力如图5（2）所示，解析法和数值法所得的经向应力结果基本一样，纬向应力结果具有良好的一致性，最大误差为2.7%，证明鹅蛋壳仿生耐压壳强度分析模型是正确的；由解析法计算所得的鸡蛋壳仿生耐压壳屈曲应力为433.00 MPa，数值法计算所得的屈曲应力为418.46 MPa，两者相差3.5%，证明鹅蛋壳仿生耐压壳屈曲分析模型是正确的。

此外，球形耐压壳、椭球形耐压壳、柱形耐压壳、抛物线形耐压壳的数值建模方法与蛋壳仿生耐压壳一致，因此，也可以认为这4种典型耐压壳的数值计算结果是正确的。

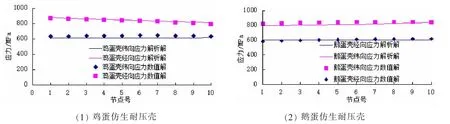
图5 仿生耐压壳理论计算与数值分析结果比较Fig.5 Comparison between theoretical and numerical results of bionic pressure hulls

3.1 蛋壳仿生耐压壳的强度和稳定性分析

图6和图7为鸡蛋壳和鹅蛋壳仿生耐压壳应力和屈曲分析结果，其中图6（2）和图7（2）分别为沿着蛋壳子午线从小端到大端的应力曲线。由图可知，由于蛋壳为轴对称结构，仿生耐压壳应力分布在绕着蛋壳长轴呈现高度对称性，仿生耐压壳应力从小端到大端先逐渐增大再逐渐减小，最小应力位于小端；蛋壳腰部位置应力较大，为结构薄弱区域，该处恰好为雏鸡和雏鹅破壳位置，现有研究表明，若禽蛋胚胎头部远离蛋壳腰部，雏禽很难破壳而出，孵化率大大降低[20]，与数值结果相互佐证。在进行蛋壳仿生耐压壳设计时，可以通过优化蛋壳厚分布、曲率半径或者采取加肋设计等方式来提高该处强度。

图6 鸡蛋壳仿生耐压壳应力及屈曲分布Fig.6 Stress and buckling distributions for the chicken pressure hull

由图6、图7可知，鸡蛋壳仿生耐压壳最大应力靠近蛋壳大端，鹅蛋壳仿生耐压壳最大应力则靠近蛋壳小端，鸡蛋壳仿生耐压壳所受最大应力比鹅蛋壳仿生耐压壳所受最大应力高7.4%；鸡蛋壳仿生耐压壳最大最小应力差值比鹅蛋壳仿生耐压壳高14.2%，说明鹅蛋壳仿生耐压壳的应力分布均匀性更好；可见，鹅蛋壳仿生耐压壳的强度特性优于鸡蛋壳仿生耐压壳。如图6（3）、图7（3）所示，鸡蛋壳仿生耐压壳的1阶屈曲特征值为3.49，具有波浪形失稳形态，失稳位置在腰部区域，波峰数n为4；鹅蛋壳仿生耐压壳的1阶屈曲特征值为4.27，也具有波浪形失稳形态，失稳位置仍然在腰部区域，波峰数n为5；鹅蛋壳仿生耐压壳的临界屈曲应力比鸡蛋壳仿生耐压壳高22.3%，证明鹅蛋壳仿生耐压壳稳定性也比鸡蛋壳仿生耐压壳好。综上所述，鹅蛋壳仿生耐压壳强度和稳定性优于鸡蛋壳仿生耐压壳，具有较好的耐压特性。

图7 鹅蛋壳仿生耐压壳应力及屈曲分布Fig.7 Stress and buckling distributions for the goose pressure hull

3.2 仿生耐压壳与4种典型耐压壳比较分析

图8为4种典型耐压壳的应力及屈曲分析结果。如图8所示，由于球形耐压壳为等强度结构，应力分布均匀性最好，在每一处基本相等，最大最小应力相差0.4%,平均应力与球形薄壳结构的理论值相差0.76%[21]。抛物线形耐压壳、椭球形耐压壳应力分布趋势与蛋壳仿生耐压壳类似，即应力从中部向两侧递减；由于结构两端也是对称的，应力分布在长轴方向也具有对称性，最大应力位于中间其对称部位，最小应力位于其两端。柱形耐压壳两半球形端所受应力最小，向柱形和半球接头处区域应力递增，柱形区域应力基本相等。球形耐压壳的屈曲特征值为7.5，屈曲特性成完全对称分布；抛物线形和柱形耐压壳屈曲特征值均为3.00，屈曲特性为沿着长轴方向半波分布的总体失稳（m=1）；椭球形耐压壳特征值3.47，波峰数n为4，屈曲特性和蛋壳仿生耐压壳类似。

为了考察仿生耐压壳的有效性，从浮力系数、壳内空间利用率、流线型、舒适性等4个方面，进行仿生耐压壳与典型耐压壳对比分析，这些耐压壳同时满足如下条件：（1）耐压壳最大等效应力≤0.79σy；（2）弹性屈曲特征值≥3.00；（3）耐压壳内部体积为4.2 m3。结果如表2所示，在设计过程中，对于鸡蛋形、鹅蛋形、球形、椭球形耐压壳，需要重点关注其强度特性，而对于抛物线形、柱形耐压壳，则需要重点关注其稳定性；球形耐压壳浮力系数最小，储备浮力能力最优，其次是鹅蛋形、鸡蛋形、柱形、椭球形、抛物线形耐压壳，其储备浮力能力分别是球的87%、82%、68%、67%和66%；从浮力系数、壳内空间利用率、流线型、舒适性方面综合比较可知，鹅蛋形仿生耐压壳是千米水深耐压设计的有效选择。

图8 4种典型耐压壳的应力及屈曲结果Fig.8 Stress and buckling results for the four classical pressure hulls

表2 仿生耐压壳与4种典型耐压壳性能比较Tab.2 Comparision between bionic pressure hulls and four classical pressure hulls

4 结论

（1）根据鸡蛋壳、鹅蛋壳的生物学特性，设计了鸡蛋壳、鹅蛋壳仿生耐压壳结构，并分别建立了这两种结构的解析模型和数值模型，研究其强度和稳定性；解析法和数值法所得的经向应力、纬向应力和临界屈曲应力基本吻合，证明鸡蛋壳、鹅蛋壳仿生耐压壳强度和屈曲分析模型是正确的。

（2）仿生耐压壳应力分布在绕着蛋壳长轴呈现高度对称性，仿生耐压壳应力从小端到大端先逐渐增大再逐渐减小，最小应力位于小端；蛋壳腰部位置应力较大，为结构薄弱区域，该处恰好为雏鸡和雏鹅破壳位置，在进行蛋壳仿生耐压壳设计时，可以通过优化蛋壳厚、曲率半径或者采取加肋设计等方式来提高该处强度。

（3）鸡蛋仿生耐压壳所受最大应力比鹅蛋仿生耐压壳所受最大应力高7.4%，鸡蛋壳仿生耐压壳最大最小应力差值比鹅蛋壳仿生耐压壳高14.2%，鹅蛋仿生耐压壳的临界屈曲应力比鸡蛋仿生耐压壳高22.3%，鹅蛋壳仿生耐压壳强度和稳定性优于鸡蛋壳仿生耐压壳，具有较好的耐压特性。

（4）对于鸡蛋形、鹅蛋形、球形和椭球形耐压壳，需要重点关注强度特性，而对于抛物线形、柱形耐压壳，则需要重点关注稳定性；球形耐压壳浮力系数最小，储备浮力能力最优，鹅蛋形、鸡蛋形、柱形、椭球形、抛物线形耐压壳的储备浮力能力分别是球的87%、82%、68%、67%和66%；综合比较可知，鹅蛋壳仿生耐压壳可为千米水深耐压设计提供有效参考。

参考文献：

[1]Reynolds T,Lomacky O,Krenzke M.Design and analysis of small submersible pressure hulls[J].Computers and Structures,1973,3(5):1125-1143.

[2]Ma L,Cui W C.Path following control of a deep-sea manned submersible based upon NTSM[J].China Ocean Engineering,2005,19(4):625-636.

[3]Liang C C,Shiah S W,Jen C Y,Chen H W.Optimum design of multiple intersecting spheres deep-submerged pressure hull[J].Ocean Engineering,2004,31(2):177-199.

[4]梁学先.潜艇耐压船体特殊问题的研究[D].哈尔滨:哈尔滨工程大学,2006. Liang X X.Study on special problem of submarine pressure hull[D].Harbin:Harbin Engineering University,2006.

[5]苏玉民,庞永杰.潜艇原理[M].哈尔滨:哈尔滨工程大学出版社,2013.

[6]Ness C C,Simpson WM.A new submarine paradigm[J].Naval Engineers Journal,2000,112(4):143-152.

[7]Blachut J,Smith P.Buckling of multisegment underwater pressure hull[J].Ocean Engineering,2008,35(2):247-260.

[8]Blachut J,Jaiswal O R.On buckling of toroidal shells under external pressure[J].Comput Struct,2000,77(3):233-251.

[9]Babich D V.Stability of shells of revolution with multifocal with multifocal surfaces[J].International Applied Mechanics, 1993,29(11):68-72.

[10]Wong H T.Behaviour and modelling of steel-concrete composite shell roofs[D].The Hong Kong:The Hong Kong Polytechnic University,2005.

[11]Pawel Woelke.Computational model for elasto-plastic and damage analysis of plates and shells[D].Baton Rouge:Louisiana State University,2005.

[12]Upadhyaya S K,Cooke J R,Gates R S,et al.A finite element analysis of the mechanical and thermal strength of avian eggs[J].Journal of Agricultural Engineering Research,1986,33(1):57-78.

[13]姜松,崔志平.不同加载方式下的鸡蛋静力学特性和有限元分析[J].食品科学,2009,30(21):90-93. Jiang S,Cui Z P.Static properties and finite element analysis of chicken eggs under different loading modes[J].Food Science,2009,30(21):90-93.

[14]Narushin V G.Shape geometry of the avian egg[J].Journal of Agricultural Engineering Research,2001,79(4):441-448.

[15]喻九阳.压力容器与过程设备[M].北京:化学工业出版社,2011.

[16]Babich D V.Stability of shells of revolution with multifocal with multifocal surfaces[J].International Applied Mechanics, 1993,29(11):68-72.

[17]中国船级社.潜水系统和潜水器入级与制造规范[M].北京:人民交通出版社,1996.

[18]Wong S I.Department of precision and microsystems engineering on lightweight design of submarine pressure hulls[M]. Holland:Structural Optimization and Computational Mechanics,2012.

[19]Liang C C,Shiah S W,Jen C Y,Chen H W.Optimum design of multiple intersecting spheres deep-submerged pressure hull[J].Ocean Engineering,2004,31(2):177-199.

[20]Narushin V G,Romanov M N.Egg physical characteristics and hatchability[J].World’s Poultry Science Journal,2002,58 (3):297-303.

[21]Ventsel E,Krauthammer T.Thin plates and shells theory,analysis,and applications[M].Boca Raton:The Chemical Rubber Company Press,2001.

Bionic design and analysis of deepwater pressure hull

ZHANG Jian1,2,WANG Wei-bo1,GAO Jie2,WANG Ming-lu2,TANG Wen-xian2,WU Wen-wei1
(1.China Ship Scientific Research Center,Wuxi 214082,China;2.Jiangsu University of Science and Technology, Zhenjiang 212003,China)

The design theory and analysis method of kilometer water-depth bionic pressure hull for eggshell were presented.Shape function for chicken eggshell and goose eggshells was proposed,using Upadhyaya equation and N-R equation,respectively.Secondly,bionic pressure hulls of the chicken eggshell and goose eggshell with the water depth of 6 km were designed,and strength and stability of the two hulls were investigated based on analytical method and numerical method.Finally,numerical models of four classical pressure hulls,including spherical hull,parabolic hull,cylindrical hull and ellipsoidal hull,were employed for comparison with the two bionic pressure hulls.The results showed that,meridional stress,zonal stresses and critical buckling stresses from the numerical method agreed well with the analytical method.The goose pressure hull has perfect pressure resistance,whose strength and stability were better than the chicken pressure hull.Spherical pressure hull has the most buoyancy reserve capacity.Buoyancy reserve capacity for goose pressure hull,chicken pressure hull,cylindrical pressure hull,ellipsoidal pressure hull,parabolic pressure hull was respectively 87%,82%,68%,67%,66%of the spherical pressure hull.Goose pressure hull could provide effective guide for the design of deepwater pressure hull,considering buoyancy reserve, interior layout and hydrodynamics.

U661.4TE58

A

10.3969/j.issn.1007-7294.2015.11.009

1007-7294（2015）11-1360-08

2015-07-31

国家自然科学基金项目（51205173）；江苏省基础研究计划（自然科学基金）—青年基金项目（BK20150469）

张建（1984-），男，博士后，E-mail：zhjian127@163.com；

王纬波（1969-），男，研究员。