铰连接在深水S型铺管中的应用

宋林峰，孙丽萍，钱佳煜，武春霖

（哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001）

铰连接在深水S型铺管中的应用

宋林峰，孙丽萍，钱佳煜，武春霖

（哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001）

为了能够在S型铺管过程中将管线、船体和托管架三者作为一个整体进行耦合分析，使用势流理论用于计算船体受到的波浪力，广义弹性接触面法模拟托辊与管线之间的接触，采用带有铰接刚度的铰连接来模拟管线的上弯段，集中质量法用于模拟管线的中垂段和下弯段。通过时域全耦合方程将整个系统联立求解，并将这种方法的结果和未考虑上弯段管线接触的结果与实验值进行了对比发现：新计算方法能够使管线受力和船体运动都更为接近于实际值。对管线张力进行了谱密度分析，得到了对管线张力作用较大的频谱范围，为其在不同海况下的适应性提供了技术参数。

铰连接；S型铺管；弹性面接触；集中质量法

0 引言

随着海洋石油天然气开发的水深不断加深，海洋管道的作用显得越来越重要。由于使用铺管船铺设海底管道相对于其它方法来说具有更强的抗风浪能力、更广的适用性、更加机动灵活和更高的作业效率等优点，它已成为铺设海底管道最主要的方法之一。

目前铺管方法主要有S形铺管法、J形铺管法、卷筒式铺管法以及垂直铺管法。最深的铺管水深已达到3 000 m左右。在S型铺设时，管线在铺管船托管架的支撑下，自然弯曲成S型，因而得名。采用S型铺设的铺管船，一般都具有较多的管线焊接站，往往具有较高的管线预制速率[1]。管道部分一般分为三个部分：上弯段，中垂段和下弯段。S型铺管由于其焊接速度快，铺设速度快的原因在深水区域小管径铺设通常选用S型铺管来降低铺设造价[2]。

随着S型铺管铺设的深度不断加深，技术上遇到了很多挑战，铺设过程中管线承受重力、拉力、水动力、扭转、弯曲、内部和外部流体静压力、海底摩擦力等综合作用，并且恶劣的海况和复杂的海底条件都给深水铺设带来更大的挑战。目前对S型铺设中对管道的分析通常是将船体与管道进行解耦分析，主要是由于托管架上管道的上弯段不能用常用的系泊锚缆方法进行分析。并且在管道铺设过程中需要考虑管线与支撑结构之间的接触机理，特别是托管架的支撑托辊与管线的接触。

为了解决深海铺设带来的困难，国内外学者在原有理论的基础上不断地提出新的研究方法。Riaan[3]针对带有水下托管架的铺管船，提出将船体和托管架作为一个整体进行分析，得到了船体具有托管架载荷影响的运动响应。Silva[4]使用SITUA-Prosim软件模拟了铺管船铺管过程。托管架上托辊与管线之间的接触通过基于方位和接触面的接触刚度来实现。Martinez和Goncalves[5]使用弹簧边界条件模拟了托辊以及管土耦合部分，并建立数学模型分析了管线应力。Jensen[6]考虑了系泊作用对船体的影响，但文中针对的是J型铺管船，无托管架对船体的影响。李金玉[7]通过实验证明，铺管船管线张力主要由垂荡和纵摇导致，并且通过离散管线与连续管线两种实验模拟方法得到了不同水深的张力结果。宋林峰[8]考虑了托管架对管线的影响作用，并对船体—托管架—管线三者之间的耦合关系进行了模拟，而且还考虑了动力定位这种新型的系泊方式。

铰连接在海洋工程中目前已经得到了广泛的应用，Newman，Sun，勾莹[9-11]分别使用不同的方法对2个铰连漂浮方箱进行了水动力计算。沈庆[12]使用多刚体力学的凯恩方法对浮基多刚体系统进行动力分析，并应用于计算浮基系统。江召兵[13]使用齐次矩阵法计算多刚体系统，用于求解浮基的动力特性。Ranney[14]使用铰接方法在频域内计算了FPSO外输旁靠系统。Sun Liping[15]用铰接模拟软钢臂在时域内得到了安全外输工况。

本文在文献[8]的基础上对铰接模型进行了完善，将托辊上的管线弯矩进行了考虑，将其模拟为铰接刚度，并与实验结果进行了对比。上弯段的管线被离散成多个相互铰接且具有铰接刚度的莫里森杆元，托管架与管线接触分析方法使用弹性面接触算法，整个系统考虑了船体和管线之间动力和非线性影响。

1 理论研究

1.1 时域运动耦合

三维势流理论用于计算浮体的水动力系数以及波浪力。为了能够分析铺管船受到的低频和高频波浪力，QTF用于计算得到平台的二阶波浪力。计及势流阻尼的记忆延时效应，卷积积分用于计算平台的辐射力。铺管船时域耦合方程为：

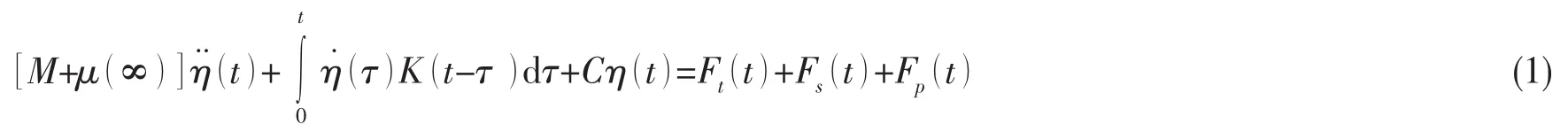
其中：Ft（t）是风、浪、流对船体随时间变化的作用力，并且包括托管架所受到的波浪力；Fs为托辊接触模型对船体的反作用力；Fp为管线对船体的作用力。

公式（1）能够对船体运动和管线结构响应进行联立求解，并能够考虑船体和管线之间的动力和非线性影响。托管架与管线接触通过基于方位和接触面的接触刚度的总的刚度矩阵来模拟。

1.2 管线力学方法

管线上弯段的拱形形状是因为有托管架上托辊的支撑作用，在面元法中很难模拟。在设计托管架时通常使用线性弹簧来模拟两个节点之间的接触。在本文中使用了广义弹性面接触方法，根据两个面的方位和接触面的刚度来模拟接触[16-17]。

将托管架上的管线模拟为由Morison杆组成的多刚体系统，每一个分段为一个独立刚体，彼此间运动约束关系抽象为铰接，通过铰接来传递力与弯矩。根据彼此间相对运动的特征定义其铰接的自由度。本文将托管架上的管线定义为万向铰[18]模式，能考虑管线的弯曲但忽略管线的扭转作用。

每两个结构之间的铰接点通过角加速度和线加速度来组成控制方程：

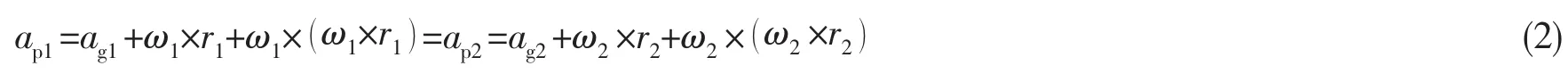
其中：api为结构i上铰接点的平移加速度，agi为i结构上重心的平移加速度，ωi为结构i的转角加速度，ri为结构i的重心至铰接点的向量。

多根Morison杆彼此铰接，并计及铰接刚度。在原有的铰接传递方程的基础上加入了铰接刚度的影响，用以模拟管线的弯曲刚度。公式（3）用于描述管线上弯段受到的弯矩。

式中：M为管线的弯矩，EI为管线的弯曲刚度，K为铰接刚度，C为铰接阻尼，α1为管线弯曲曲率，α2为铰连接的相对转角。

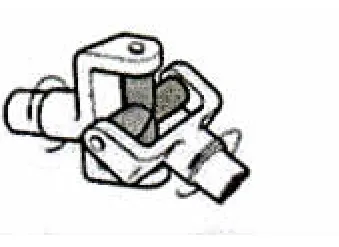
图1 a万向铰Fig.1a Universal joint

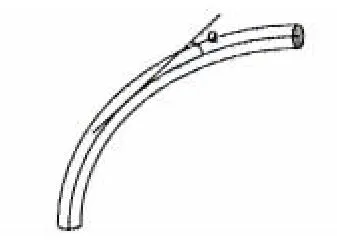
图1 b管弯曲曲率Fig.1b Bending curvature of tube

图1 c铰接相对转角Fig.1c Hinged rotation

为了能够考虑管线的弯曲应力以及轴向应力，管线的中垂段和下弯段使用了集中质量法[19]来计算得到管线的弯曲应力和轴向应力。

通过将集中质量法得到的管线张力加入时域全耦合方程（1）中使整个模拟过程较为完整。整个模拟过程考虑了管线、托管架、船体以及彼此之间的相互作用力，是一个完整的全耦合分析。使用Newmark-β法以及Newton-Rapson迭代对时域耦合方程求解可以得到系统各部分的运动以及受到的力。

2 数值模拟

本文使用中海油在役的深海起重铺管船201为计算模型，在水深为2 000 m的深水区作业。深海起重铺管船的船型参数如表1所示。

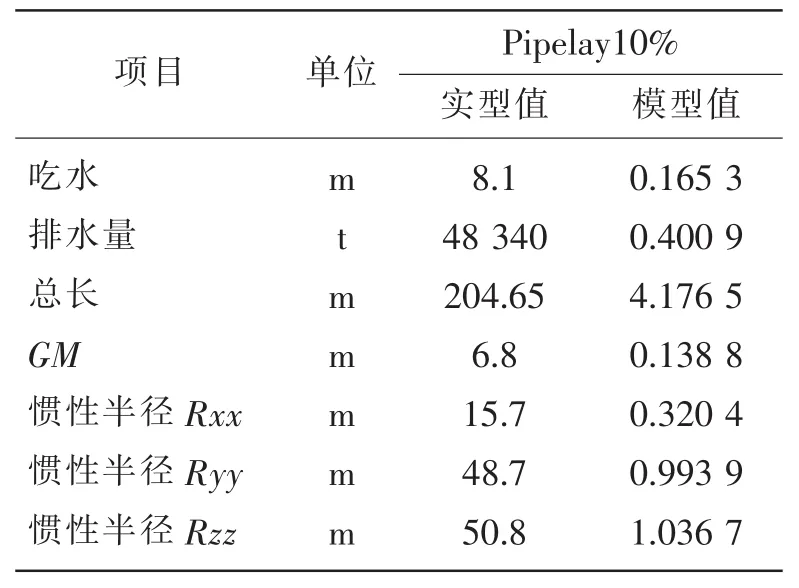
表1 铺管船主要参数Tab.1 Pricipal dimension of lay barge

建立船体面元网格如图2所示。托管架采用三段式桁架式铰接托管架，通过调整各段之间的相对角度以及托辊支撑的高度，实现一定范围内的半径变化。

在图3中，托管架上模拟托管的U型支撑。托辊对管线的支撑作用通过图4可以有较为直观的了解。托管架为3段式连接，滑道半径为73 m，三段托管架分别长33 m，27 m和29，m。为了能够更加准确地模拟托辊对管线的反作用力，将文献[8]中的垂直向上的托辊改为实际托辊支撑方向，这在一定程度上更接近于实际情况，并且可通过调节托辊角度来得到不同的托辊倾斜角度对上弯段的弯矩的影响如图5（左）所示。图5（右）为数学模型。

图2 船体模型Fig.2 Model of ship

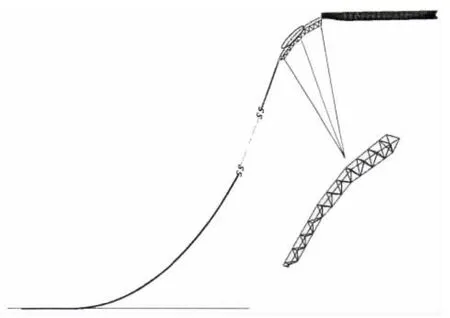
图3 铺管状态下铺管船总体示意图Fig.3 Diagram of lay barge in the process of pipelaying

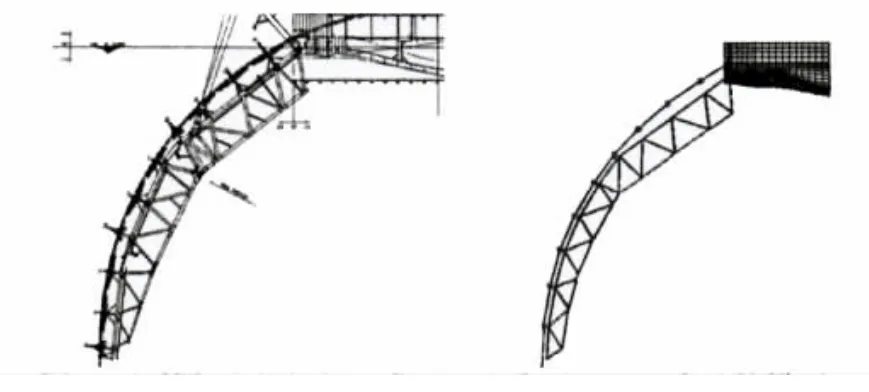
图4 托管架上的托辊示意图（左为图纸，右为计算模型）Fig.4 The diagram of roller on stinger

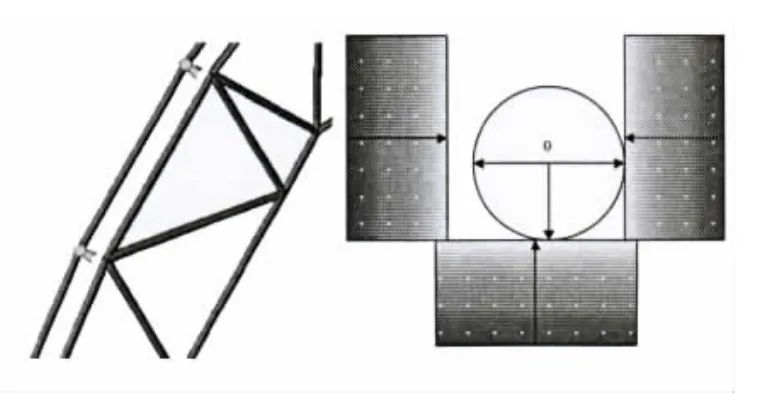
图5 接触模型Fig.5 The contact model

3 结果与讨论

采用Jonswap谱模拟随机波浪载荷，恒定风速产生的载荷使用Oil Companies International Marine Forum（OCIMF）推荐的系数及公式进行计算。铺设水深为2 000 m，管线外径0.324 m。

实验与数值模拟的环境条件如表2所示。

表2 环境条件Tab.2 The environment condition

3.1 时域运动响应分析

铺管船的运动对管线的轴向张力影响主要体现在垂荡与横/纵摇方向。本文主要针对垂荡、纵摇两个方向上的船体运动进行分析，并将该结果与未考虑非弹性接触以及托管架上管线受力的传统计算方法的结果进行了对比。为了阐述方便，我们把将管线考虑为系泊线系于托管架末端的方式记为方法1，将考虑了管线与托辊间的非线性接触计为方法2，将既考虑了管线与托辊之间的非线性接触也考虑了上弯段管线的弯曲刚度记为方法3。值得注意的是，方法3中上弯段管线的弯曲刚度使用带有铰接刚度的铰接形式来模拟。表3和表4分别为环境力为船首入射的角度下三种方法的垂荡与纵摇方向的运动统计分析与实验值[7]的对比。

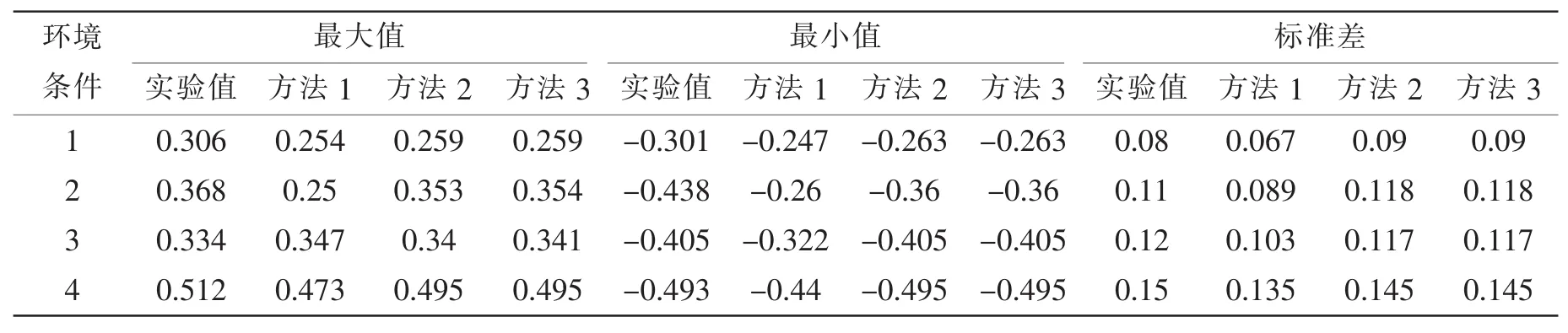
表3 垂荡方向不同的计算方法与实验对比Tab.3 Heave motion of ship with different methods comparing to model test

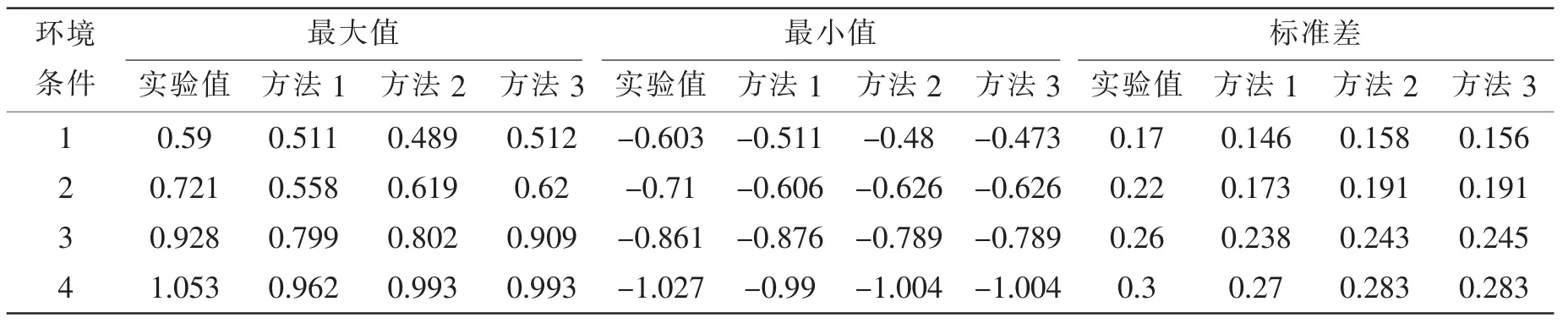
表4 纵摇方向不同的计算方法与实验对比Tab.4 Pitch motion of ship with different methods comparing to model test

分析表3-4可以发现，随着波浪周期的增加垂荡和纵摇的最大值也随之增加。分析不同工况下标准差发现，随着波浪周期的增大船体的振荡值也随之增大，尤其是在垂荡方向上，标准差的增幅达到了46%。这也说明了波浪周期对铺管船的操作影响较大。

根据不同的分析方法发现：在垂荡和纵摇方向上，与方法1、2相比，通过方法3得到的结果大多数情况下都更为接近于实验值，且方法2，3值较为接近，方法3介于方法1与实验值之间。通过对数据的分析，我们发现，方法1会低估环境条件对船体运动幅值的影响。尤其是在初始设计阶段，对船体运动幅值的低估也会造成绞车能力或推进器推力的低估。

3.2 管线张力动态分析

铺管过程中，管线上弯段受力最大的部分通常在管线脱离托管架的部分。由于模型试验较难捕捉到管线的弯曲应力，所以本文仅对使用三种方法对管线脱离托管架部分的张力进行了分析，并与实验值进行了对比。表5详细列出了不同的计算方法在环境力为船首入射的角度下的张力统计值。

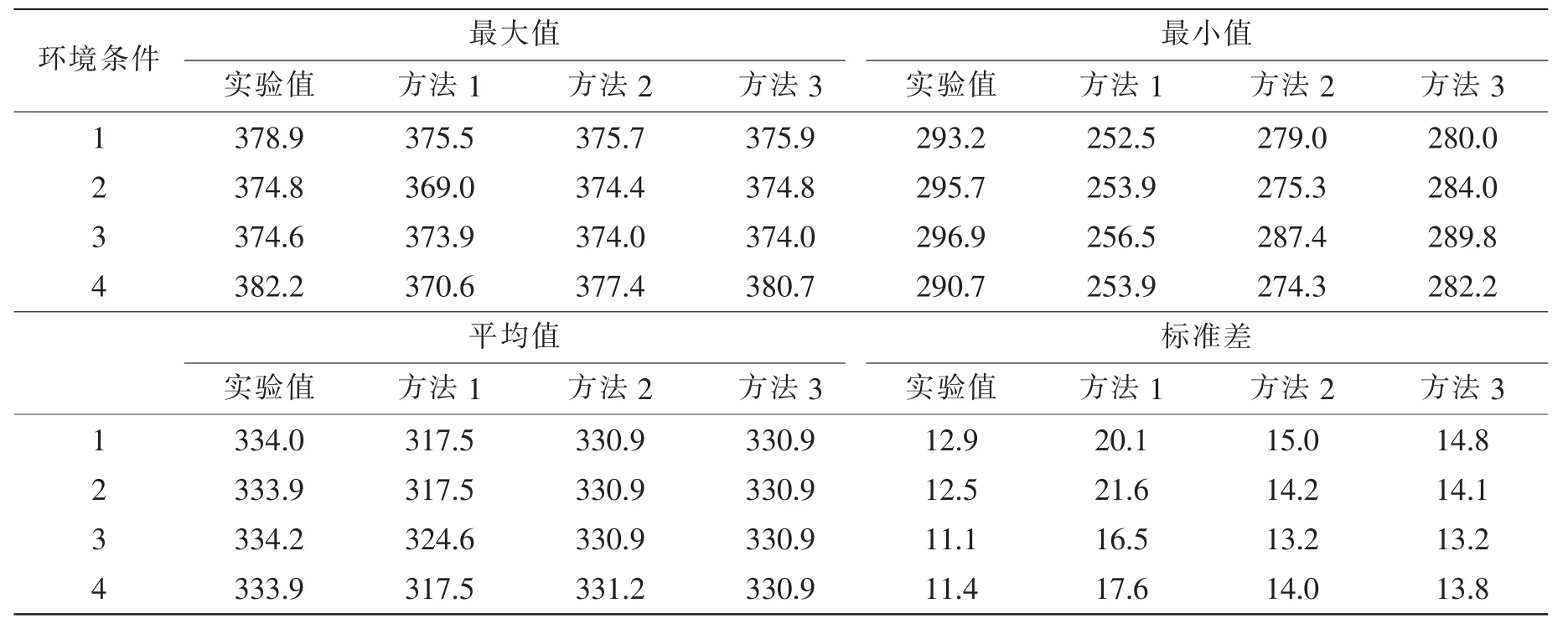
表5 管线张力基于不同的计算方法与实验对比Tab.5 The tension of pipe with different methods comparing to model test

通过对比表5中的三种方法与实验值对比可以发现，方法3的最小值，均值以及标准差皆介于方法1与实验值之间，但是最大值皆超过实验值与方法1。以环境条件4为例，方法3的最大值，最小值，均值和标准差与实验值对比偏差分别为0.39%，2.92%，0.9%和21.05%；方法2分别为1.26%，5.46%，0.81%和22.81%；方法1分别为3.04%，12.66%，4.91%和54.39%。由此可见方法3这种新计算方法考虑得更全面且在计算管道张力方面具有一定的优越性。而方法2与方法3之间相差较小，且方法2由于未考虑上弯段的管道弯矩的影响而计算速度相对方法3更快，所以为了能够节省计算耗时可以使用方法2来提高计算效率。方法1和方法2与实验值的对比可以发现，接触模型对船体运动和管线张力的计算精度提高十分明显，说明管线受到环境载荷的作用对船体和托管架有较大作用力。通过对方法2和方法3与实验值的对比发现，考虑管线上弯段弯曲刚度对船体运动以及管线张力的计算精度略有提高，但计算耗时明显增加。

3.3 管线张力对波浪的敏感性分析

铺管船在铺管工况下，铺管船运动对波浪敏感性分析具有较为重要的意义，同样，管线的波浪敏感性分析同样重要。用全QTF矩阵计算波浪的和、差频对船体的二阶力，从而分析管线对应不同波浪频率的敏感性。

以环境条件1为例，通过对其管线张力进行谱密度曲线分析可以得到的谱密度曲线如图6所示。其中低频定义为小于0.2 rad/s，波频定义为0.2 rad/s至1.5 rad/s。功率谱密度值—频率值的关系曲线下的面积就是方差，即响应标准差的平方值。所以根据频谱密度曲线我们可以统计出低频以及波频对铺管船两种工况的影响。从曲线峰值所在的区域很容易发现，管线张力集中于波频范围，从而确定波频是管线张力的主要原因。并且在0.7 rad/s至0.9 rad/s波浪频率内管线张力较大。

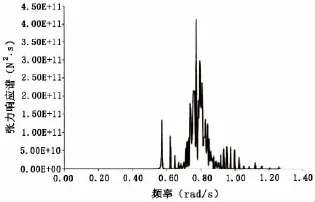
图6 环境条件1下管线张力响应谱Fig.6 The tension spectrum of pipe under the sea state 1

4 结论

为了能够完整地模拟S型铺管过程中上弯段复杂的接触模型对整个铺管过程的影响，本文对托辊与管线之间的接触使用广义弹性接触面法来模拟，采用带有铰接刚度的铰连接来模拟管线的上弯段，通过时域全耦合方程将整个系统联立求解，对计算结果的分析可以得到以下结论：

（1）通过与实验值对比发现，考虑管线上弯段的接触模型以及弯曲刚度能够更好模拟船体的运动以及管线张力。

（2）方法1和方法2与实验值的对比发现：接触模型对船体运动和管线张力的计算精度提高十分明显，说明管线受到环境载荷的作用对船体和托管架有较大作用力，建议在实际工程中将接触模型考虑在内。

（3）方法2和方法3与实验值的对比发现：考虑管线上弯段弯曲刚度对船体运动以及管线张力的计算精度略有提高，但计算耗时明显增加。

（4）通过对管线张力的谱分析可知，管线张力受波频影响较大，并且在0.7 rad/s至0.9 rad/s波浪频率内管线张力较大。

在模拟铺管船铺管工况时应考虑管线—托管架—船体三者与波浪的耦合作用，传统的计算方法并不能真实地反应铺管船的运动，而铰连接这种模拟上弯段的方式具有数据可靠性，可应用于S型铺管的数值模拟。

托管架上托辊的布置角度对管线的整体形态和受力皆有较大影响，所以托管架和托辊的布置是需要进一步研究的目标。

[1]曲俊生,刘文利,蔡连博.我国海底管道铺设及铺管船的发展[J].中国水运,2013,13(9):311-313. Qu Junsheng,Liu Wenli,Cai Lianbo.The development of submarine pipeline laying and laying ship in China[J].China Water Transport,2013,13(9):311-313.

[2]宋儒鑫.深水开发中的海底管道和海洋立管[J].船舶工业技术经济信息,2003,06:31-42. Song Ruxin.The deep sea development of submarine pipeline and the riser[J].China Academic Journal Electronic Publishing House,2003,06:31-42.

[3]Veer R V.Application of linearized Morison load in pipe lay stinger design[C]//Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering.Estoril,Portugal,2008:247-256.

[4]Silva L D,Lima H M,Jacob B P.Pipeline-lay barge interaction model for the simulation model for the simulation of S-lay installation procedures[C]//Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering.Estoril,Portugal,2008-58487.

[5]Martinez C E.Laying modeling of submarine pipelines using contact elements into a corotational formulation[J].Journal of Offshore Mechanics and Arctic Engineering Copyright,2003:125,145-152.

[6]Jensen G A.Modeling and control of offshore marine pipeline during pipelay[C]//17th World Congress,International Federation of Automatic Control.Seoul,Korea.2008:15034-15039.

[7]李金玉.起重铺管船水动力性能研究[D].上海:上海交通大学,2010:86-90. Li Jinyu.Study on pipelay derrick vessel hydrodynamics[D].Shanghai:Shanghai Jiao Tong University,2010:86-90.

[8]宋林峰,孙丽萍,王德军.深水S型铺管托管架-船体-管线耦合分析[J].哈尔滨工程大学学报,2013,34(4):415-420. Song Linfeng,Sun Liping,Wang Dejun.Coupling analysis of stinger-lay barge-pipeline of S-lay installation in deep water[J].Journal of Harbin Engineering University,2013,34(4):415-420.

[9]Sun L.Response of interconnected floating bodies[J].Civil&Structural Engineering,2011,4(3):143-156.

[10]Newman J N.Wave effects on deformable bodies[J].Applied Ocean Research,1994,16:47-59.

[11]勾莹,滕斌,宁德志.波浪与两相连浮体的相互作用[J].中国科学工程,2004,6(7):75-80. Gou Ying,Teng Bin,Ning Dezhi.Interaction effects between wave and two connected floating bodies[J].Engineering Science,2004,6(7):75-80.

[12]陈徐均,沈庆,崔维成.浮基多刚体系统动力分析[J].工程力学,2002,19(5):139-143. Chen Xujun,Shen Qing,Cui Weicheng.Analysis of dynamic behavior of a multi-rigid-body system with a floating base [J].Engineering Mechanics,2002,19(5):139-143.

[13]江召兵,杜乃娟,陈徐均等.浮基多体系统在波浪中展开的数值模拟[J].海洋工程,2011,29(4):114-118. Jiang Zhaobing,Du Naijuan,Chen Xujun.Numerical simulation for the expansion of floating-base multibody system excited by wave[J].Ocean Engineering,2011,29(4):114-118.

[14]Ranney R S.Random dynamic analysis of multi-body offshore structures[J].Ocean Engineering,1984,11(4):381-401.

[15]Sun L P,He Q,Ai S M.Safety assessment for a side-by-side offloading mooring system[J].Journal of Marine Science and Application,2011,10:315-320.

[16]Silva D M L,Pereira A C P,Jacob B P.A contact model for the simulation of line collision in offshore oil exploitation[C] //Procs of the XXVIII Latin American Congress on Computational Methods in Engineering.Port,Portugal,2007:22-35.

[17]Silva D M L,Corrêa F N,Jacob B P.A generalized contact model for nonlinear dynamic analysis of floating offshore systems[C]//Procs of the 25th Int.Conf.on Offshore Mechanics and Arctic Engineering.Hamburg,Germany,2006-92155.

[18]沈庆,陈徐军,江召兵.浮体和浮式多体系统流固耦合动力分析[M].第1版.北京:科学出版社,2001:155-157. Shen Qing,Chen Xujun,Jiang Zhaobing.Floating body and floating multi-body system of fluid-solid coupling dynamic analysis[M].1st edition,Beijing:Science Press,2001:155-157.

[19]Low Y M,Langley R S.Time and frequency domain coupled analysis of deepwater floating production systems[J].Applied Ocean Research,2006,28:371-385.

[20]朱晓环,李丽娜,罗超.新型深水立管提升系统设计及展望[J].中国造船,2013,54(1):181-188. Zhu Xiaohuan,Li Lina,Luo Chao.Development of a new type of deeper water risers lifting system[J].Shipbuilding of China,2013,54(1):181-188.

Application of hinged connection in deep water S-lay installation

SONG Lin-feng,SUN Li-ping,QIAN Jia-yu,WU Chun-lin
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)

In order to take the pipeline,lay barge and stinger as a coupled system in the S-lay process,the potential flow theory was used to calculate the wave forces acting on the hull.A method utilizing a generalized elastic surface contact algorithm was used to simulate the contact between pipeline and roller.The upper curved section of pipeline was connected by hinged with considering the hinged stiffness and the sagging,and lower horizontal section of pipeline was calculated by lumped mass method.The line tension and hull motion results were obtained by the full-coupled time domain equations of the whole system,and the results were compared to experiment results and the statistics without considering the contact of the pipeline and hull.It is found that pipeline tension and hull motion results are closer to the actual values by hinged method with considering the hinged stiffness.The spectral density analysis was carried out on the line tension and acquired the frequency range in which occur the larger line tensions,and it can provide technical parameters for the adaptability of lay barge in different sea condition.

hinged connection;S-Lay method;elastic surface contact;lumped mass method

P75

A

10.3969/j.issn.1007-7294.2015.11.007

1007-7294（2015）11-1344-08

2015-02-27

国家高等学校学科创新引智计划基金资助（B07019）；工业和信息化部高技术船舶科研计划重点项目“3 000 m水深大型起重铺管船自主研发”。

宋林峰（1988-），男，博士生，E-mail：7781902@163.com；

孙丽萍（1962-），女，教授，博士生导师。