船用气囊隔振系统的非线性动力学特性

刘渊博，李明，何琳

（1西安科技大学理学院力学系，西安710054；2海军工程大学振动与噪声研究所，武汉430033）

船用气囊隔振系统的非线性动力学特性

刘渊博1，李明1，何琳2

（1西安科技大学理学院力学系，西安710054；2海军工程大学振动与噪声研究所，武汉430033）

气囊隔振系统通常被广泛应用于对舰船或潜艇上的大型旋转机械实施隔振控制。然而，船舶在航行时，隔振系统有时会产生过大的位移，会呈现出一些非线性动力学现象。文中以带间隙的线性弹簧限位器的隔振系统为研究对象，考虑了垂直和偏转两个方向的运动，基于分析力学的相关理论建立了具有旋转偏心质量的气囊隔振系统非线性动力学模型，并且采用数值方法重点分析了该系统的非线性动力学行为以及参数变化对系统动力学特性的影响。结果显示在低转速时，系统呈现出准周期运动特性；随着转速的增大，系统运动中出现混沌、周期3、5、7及准周期运动等一系列的非线性动力学现象。

气囊隔振器；限位器；分段线性；非线性动力学

0 引言

舰船在航行时，船上设备工作而产生的机械振动是噪声的主要来源之一。对于军用舰艇，动力系统的机械振动噪声严重影响其隐蔽性，因此研究船舶机械系统的减振降噪对舰艇的安全性具有重要意义[1-2]。

船舶的机械系统的隔振技术经过了多次技术跨越，其隔振效果不断提升[3-4]。目前常用隔振系统主要有单层、双层及浮筏隔振系统等。单层隔振装置其主要用于隔振要求不高的舰船设备，以及有严格对中要求的推进动力系统[5]。双层隔振是在设备和基座之间安装两层隔振器，并在两层隔振器之间插入中间质量块，利用中间质量衰减隔振器传递来的振动，从而提高隔振效果[6-7]。浮筏隔振系统是在单层和双层隔振系统的基础上发展起来的一种新型隔振装置，能够更好地抑制振动能量在系统中的传递[8]。

一般而言，气囊隔振系统是一种具有非线性振动特性的隔振装置[9]，可以将其力学特性按照实际需要进行理想设计，以满足现实减振需求[10]。而含限位器的气囊隔振装置由于具有分段弹性特征，因此涉及到非线性动力学系统建模，多刚体动力学计算仿真和优化等多学科大型分析计算问题[11]。文献[12]对具有主动隔装置的浮筏系统进行动力学建模，采用了一种新型手段分析了系统的隔振特性；文献[11-13]则采用伪力法讨论了带有限位器的浮筏隔振系统的冲击响应，分析了限位器参数对冲击响应的影响；文献[14]建立了多自由度弹性限位浮筏隔振系统的线性动力学模型，并通过人工神经网络算法用于判别限位器之间存在最优间隙；而文献[15]则基于有限元方法研究了囊式空气弹簧隔振器的隔振特性，并对舰用气囊隔振器隔振特性进行了评估；文献[16]通过考虑到筏体的刚体运动和弹性变形的耦合，讨论了弹性浮筏隔振系统进行动力学建模并分析了其动力学特性。

以上研究主要针对浮筏隔振系统的线性问题开展研究工作，主要讨论了系统的减振特性、冲击响应、结构优化等。本文重点研究含有限位器的船用隔振系统的非线性动力学模型，分析了该系统的非线性动力学特性和参数变化对系统动力学特性的影响。

1 气囊隔振系统动力学模型

图1所示为支承在气囊上的旋转机械系统示意图，其中的浮筏和机械设备看作是一个质量单元，气囊隔振系统的限位器安装在基础部位。旋转部件的质量偏心所产生的离心力为该系统的主要激振力，设气囊的总质量为m，转子的偏心质量为me，偏心距为e，转子的角速度为ω。

图1 气囊隔振系统模型Fig.1 The model of air-bag vibration isolation system

图2 分段线性弹性力Fig.2 Piecewise linear elastic force

对上述系统本文主要考虑系统随质心平动位移xO和绕质心的θ方向的运动，因此可以简化为两自由度系统。如果隔振器和限位器的弹性力为线性时，则系统的弹性恢复力具有分段线性特性，如图2所示。

2 气囊隔振系统运动方程

以气囊未变形位置为坐标原点，则可知偏心质量的垂直方向上的位移为xO+esin（ωt+θ），水平方向上的位移为e-ecos（ωt+θ）。

设坐标xA，xB，分别为气囊的变形，如图3所示，则坐标转换关系为

图3 变形后的气囊隔振系统Fig.3 Isolation system of deformed air-bag

设气囊隔振系统所受的是线性阻尼，并只考虑到系统垂直振动方向的阻尼，则线性阻尼力，因此，系统的Rayleigh耗散函数可表示为

此时，具有Rayleigh耗散函数的Lagrange方程为

则采用Rayleigh耗散函数获得Lagrange振动微分方程为

式中明显具有非线性特性，其中包含了系统的结构参数和运动参数。其中δA和δB函数分别表示气囊受到较大冲击力时，限位器所产生的变形，

3 无量纲化方程

为使所研究的内容具有更广泛的适用性，引入限位器间隙δ作为振动微分方程的特征长度，以δ、m和JO作为基本量纲，并为了简化模型、方便计算暂不考虑限位器的影响，而对方程中各物理量进行无量纲化，为此引出如表1中所示的无量纲量。

表1 系统各物理量的量纲化处理Tab.1 Dimensionless processing of the system physical parameters

通过无量纲化后，得到振动微分方程为

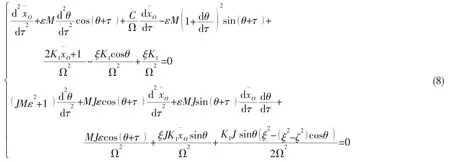
振动微分方程式变形后为

由此可以写成一阶的状态方程式，在此从略。

4 系统的非线性动力学特性

表2 系统各参数的取值Tab.2 Values of the system parameters

4.1 转速对气囊隔振系统的影响

式中具有sin（θ+τ）与cos（θ+τ）项，是典型的非线性函数，为此获得方程的解析解及近似解显得十分困难，本文采用数值方法进行求解。四阶-五阶Runge-Kutta算法通过4阶方法提供候选解，5阶方法控制误差，是一种自适应步长（变步长）的常微分方程数值解法，其整体截断误差为（Δx）5。

图4为采用45阶变步长Runge-Kutta法进行数值求解所得的位移随无量纲转速的分岔图，其中的无量纲位移O为经过充分衰减后得到的气囊隔振系统稳态响应。从图中可以看出，在低转速下系统做准周期运动。随着转速的增大，系统进入短暂的周期状态，并做周期3的运动。继续增大转速，系统则由周期3的状态进入混沌运动状态。进一步增大转速，周期—准周期—周期—准周期—…，其中出现的周期态有周期7，周期8，周期5等。

图4 稳态响应转速变化分岔图Fig.4 The bifurcation diagram of steady-state response with the parameter Ω=2.11→4.23

图5 Ω=2.224 9的准周期状态：（a）位移响应；（b)）相位图；（c）Poincaré截面Fig.5 The quasi periodic state when Ω=2.224 9:(a)Displacement response;(b)The phase orbits of vertical direction; (c)Poincaré section

图5为Ω=2.224 9时的位移响应、相位图和Poincaré截面图，从图中可以明显看出Poincaré截面图为一封闭曲线，可判断运动时准周期运动。图6是Ω=2.603 3时的运动状态，可以观察到截面图上出现成片密集点，且具有层次结构，可判定运动处于混沌状态。图7为Ω=2.784 5时的运动情况，从中可见Poincaré截面中仅出现离散的三个孤立点，即周期3的运动，系统将处于周期运动状态。

图6 Ω=2.603 3的准周期状态：（a）位移响应；（b)）相位图；（c）Poincaré截面Fig.6 The quasi periodic state when Ω=2.603 3:(a)Displacement response;(b)The phase orbits of vertical direction; (c)Poincaré section

图7 Ω=2.784 5的准周期状态：（a）位移响应；（b)）相位图；（c）Poincaré截面Fig.7 The quasi periodic state when Ω=2.784 5:(a)Displacement response;(b)The phase orbits of vertical direction; (c)Poincaré section

4.2 质量比对系统动力学特性的影响

上面考虑了无量纲转速变化时对系统的影响，下面主要讨论偏心质量比对气囊隔振系统的影响。选取系统的转速ω=1 500 r/min，考虑系统偏心质量变化范围为2 000-8 000 kg的变化。图8为Ω=3.173 4时，气囊隔振系统随质量比变化的分岔图。从图中可以看出当偏心量较小时系统处于准周期运动状态，随着偏心转速的增大，系统相继呈现出各种倍周期和准周期的非线性运动状态；当偏心质量比较大时，系统将出现周期2的稳态运动。与此同时，系统在该转速下的振幅也随着偏心质量比的增加而增加。

图8 稳态响应随质量比变化的分岔图：（a）M=0.007 142→0.010 0；（b）M=0.010 0→0.028 571Fig.8 The bifurcation diagram of steady-state response with the mass ratio change: (a)M=0.007 142→0.010 0;(b)M=0.010 0→0.028 571

5 结论

船舶在航行中由于受到多种复杂动载荷的作用，因此研究含限位器的气囊隔振系统的动力学行为具有重要的理论意义和工程实用价值。本文通过采用带间隙的线性弹簧来模拟气囊的变形，考虑了质量系统垂直和偏转两个方向上的运动，基于分析力学中Lagrange方程，建立了具有限位器的大变形气囊隔振系统的非线性动力学模型。采用45阶变步长Runge-Kutta法对非线性运动方程进行数值求解，分析了气囊隔振系统随转速和质量比变化时的非线性动力学特性。结果表明：在低转速变化情况下，系统运动状态以准周期运动为主；在中等速情况下，系统运动出现混沌态，且混沌情形保持在较宽的转速变化范围之内；在较高转速时，系统重复显现周期—准周期—周期—准周期—…的运动态，出现周期5，周期7，周期8等动力学特征。

[1]何琳,徐伟.舰船隔振装置技术及其进展[J].声学学报,2013,28(2):128-130. He Lin,Xu Wei.Naval vessel machinery mounting technology and its recent advances[J].Acta Aacustica,2013,28(2): 128-130.(in Chiniese)

[2]杨本磊.船舶浮筏隔振系统振动特性分析[D].大连:大连海事大学,2011. Yang Benlei.Research on the vibration characteristics of marine floating raft vibration isolation system[D].Dalian:Dalian Maritime University,2011.(in Chinese)

[3]吕志强,施亮等.气囊浮筏隔振装置姿态控制问题[J].噪声与振动控制,2013(1):40-44. Lü Zhiqiang,Shi Liang.Attitude control of air spring raft isolation system[J].Noise and Vibration Control,2013(1):40-44.(in Chinese)

[4]徐伟,何琳,吕志强等.船舶主机气囊隔振系统动态特性分析[J].振动与冲击,2007,26(7):122-124. Xu Wei,He Lin,Lv Zhiqiang,et,al.Dynamic analysis of an air spring mounting system for marine main engine[J].Journal of Vibration and Shock,2007,26(7):122-124.(in Chinese)

[5]朱石坚,何琳.船舶机械振动控制[M].北京:国防工业出版社,2006. Zhu Shijian,He Lin.Vibration control of onboard machinery[M].Beijing:National Defense Industry Press,2006.(in Chinese)

[6]张克国,杜清府.复杂激励下双层隔振系统的主动控制研究[J].中国机械工程,2006,17(2):134-136. Zhang Keguo,Du Qingfu.Study on active control of vibration in two-layer isolation system with multiple excitations[J]. China Mechanical Engineering,2006,17(2):134-136.(in Chinese)

[7]夏任红.某型舰船双层隔振装置的应用研究[J].船舶,2006(6):12-18. Xia Renhong.Application of double-stage vibration isolation onboard a certain naval ship[J].Ship&Boat,2006(6):12-18.(in Chinese)

[8]王久远.船舶动力系统隔振技术研究[D].武汉:武汉理工大学,2008. Wang Jiuyuan.Study of ship power system isolation technology[D].Wuhan:Wuhan University of Technology,2008.(in Chinese)

[9]Chang F,Lu Z H.Dynamic model of an air spring and integration into a vehicle dynamics model[J].Journal of Automobile Engineering,2008,222(10):1813-1825.

[10]楼京俊,朱石坚.空气弹簧特性研究[J].噪声与振动控制,2000(5):18-20. Lou Jingjun,Zhu Shijian.A study on the performance of air spring[J].Noise and Vibration Control,2000(5):18-20.(in Chinese)

[11]Jiang Guohe,Shen Rongying,Yin Liguo.Non-linear shock response calculation of shipboard equipment with displacement restrictor using pseudo-force approach[J].Journal of Ship Mechanics,2006,10(6):138-150.

[12]Niu Junchuan,Song Kongjie,Lim C W.On active vibration isolation of floating raft system[J].Journal of Sound and Vibration,2005,285(1-2):391-406.

[13]林道福,余永丰,华宏星.带限位器的浮筏隔振系统的冲击响应分析[J].噪声与振动控制,2004(1):6-9. Lin Daofu,Yu Yongfeng,Hua Hongxing.The shock response analysis of a raft isolation system with restrictors[J].Noise and Vibration Control,2004(1):6-9.

[14]温建明,冯奇.弹性限位浮筏隔振系统的动力学建模与算法[J].船舶力学,2010,14(5):449-555. Wen Jianming,Fen Qi.Model and algorithm for floating raft with elastic limiters[J].Journal of Ship Mechanics,2010,14 (5):449-555.

[15]张平豪,吴新跃.基于接触算法的气囊隔振特性分析及简化[J].船舶力学,2011,15(7):799-805. Zhang Pinghao,Wu Xinyue.Vibrating characteristic analysis and model simplification of air bag based on contact algorithm[J].Journal of Ship Mechanics,2011,15(7):799-805.

[16]王志刚,冯奇,汪玉.弹性浮筏隔振系统动力学特性及冲击响应分析[J].动力学与控制学报,2004,2(2):73-76. Wang Zhigang,Feng Qi,Wang Yu.The dynamic characteristics of a elastic raft system and its response to impact[J]. Journal of Dynamics and Control,2004,2(2):73-76.(in Chinese)

Nonlinear dynamics of the marine air-bag vibration isolation system

LIU Yuan-bo1,LI Ming2,HE Lin2
(1.Department of Mechanics,Xi’an University of Science and Technology,Xi’an 710054,China;2.Institute of Noise& Vibration,Naval University of Engineering,Wuhan 430033,China)

The air-bag vibration isolation system is widely used for suppressing the vibration of rotating machinery of a surface ship or submarine.However,when the ship is moving,this system may produce a large displacement and a nonlinear motion.In this paper,the motions of the air-bag vibration isolation system with a clearance are considered in the vertical and angular directions,and its mathematic model is developed based on the theory of analytical mechanics.Then its nonlinear dynamical behaviors are analyzed mainly by the numerical method,as well as the attention is paid to parametric effects of dynamic characteristics.The results show that there exists a quasi periodic motion at low speeds,and with increasing the rotating speed,the responses present a series of nonlinear phenomena such as periods 3,5,7,quasi periodic motion and the chaotic oscillations,etc.

air-bag vibration isolation;elastic constrain;piecewise linear;nonlinear dynamics

O322

A

10.3969/j.issn.1007-7294.2015.11.012

1007-7294（2015）11-1385-08

2015-02-28

国家自然科学基金项目（11372245）；陕西省自然科学基金项目（2014JM1015）

刘渊博（1989-）男，博士研究生，E-mail：liuyuanb0@163.com；

李明（1963-）男，教授，博士生导师，E-mail：Limingnuaa@hotmail.com。