谐振面力作用下的无穷大双周期加筋板的振动响应分析

周海安，王晓明，宋凤敏，梅玉林

（1山东理工大学机械工程学院，山东淄博255049；2大连理工大学a.机械工程学院；b.汽车工程学院，辽宁大连116024；3山东水利职业学院，山东日照276826）

谐振面力作用下的无穷大双周期加筋板的振动响应分析

周海安1，王晓明2a，宋凤敏3，梅玉林2b

（1山东理工大学机械工程学院，山东淄博255049；2大连理工大学a.机械工程学院；b.汽车工程学院，辽宁大连116024；3山东水利职业学院，山东日照276826）

文章主要研究了流体负载下的无穷大双周期加筋薄板，在周期谐振力作用下的振动响应。假设薄板和加强筋只存在法向力的作用，通过薄板和加强筋的位移连续条件，以及格林函数及傅立叶变换公式的应用，建立了频域内双周期加筋薄板的振动位移方程。利用空间波数法，将加筋薄板的振动位移表达为波数分量的迭加形式。通过数值计算的方法对波数分量进行求解，最后通过方程的傅立叶逆变换，得到了加筋薄板的振动方程。数值计算的结果表明文中的计算方法收敛速度快。

振动响应；加筋板；格林函数；空间波数法

0 引言

加筋板是许多工程结构的组成部分，在工程界得到了广泛的应用，尤其在机械，船舶和航天领域，加筋板的应用更为常见。到目前为止，许多学者对加筋板的振动特性进行过研究，并且提出了许多不同的求解方法[1-8]。然而大部分的科研工作主要集中在有限尺寸或单周期无穷大加筋板的振动研究上，而对于水下无穷大双周期加筋薄板振动响应的研究则要少得多。本文的主要目的是寻求一种合适的数学方法以便对双周期加筋薄板结构进行振动分析。但是由于加筋薄板的周期性以及流固耦合问题的复杂性，几种重要的数学方法如Rayleigh-Ritz能量法﹑有限差分法﹑传递矩阵法﹑模态法等并不能很好地解决无穷大周期结构的振动问题。由Mead和Pujara[9]提出的空间波数法在处理流固耦合的周期结构振动问题上体现出了明显的优势：Mace[1]在空间波数法的基础上，推导出流体作用下双周期加筋薄板的振动和辐射声压方程，并且分析了点力作用下的水中远场辐射声压。Lee和Kim[10]等亦通过空间波数法对单周期加筋薄板的振动响应及声透射系数进行了理论分析与计算。此外，傅里叶变换的方法也是研究结构振动和声辐射的一种有力工具。吴文伟等[11]曾经采用傅里叶变换的方法对单周期加筋薄板的声辐射进行过研究。

本文对水下无穷大双周期加筋薄板的振动响应进行了分析，并且根据格林函数与空间波数法以及傅里叶变换法，建立了加筋薄板的振动方程，并最终通过数值计算的方法得到了方程的解。在计算结果中，本文重点分析了加强筋横截面尺寸以及周期间距等几个主要物理参数对薄板振动响应带来的影响。

1 加筋薄板的振动方程

1.1 数学模型

无穷大双周期加筋薄板的上表面空间充满水流体，薄板的下表面空间是空气。在x轴方向的加强筋沿x=mLx周期排列，在y轴方向的加强筋沿y=nLy（m，n=0，±1，…，±∞）周期排列，周期加筋薄板的局部结构示意图如图1所示。

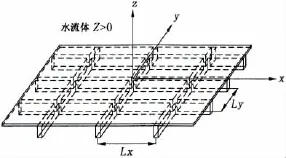
图1 双周期加筋薄板Fig.1 Diagram of the two-dimensional beam-stiffened plate

双周期加筋薄板受到随时间t周期变化的谐振面力f（x，y）exp（jωt）的作用，其方程表达式是[1]

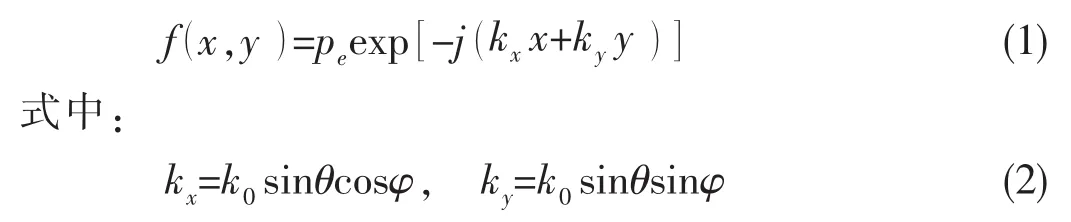
pe是谐振力的幅值，ω是圆频率，k0是谐振力波数，θ是谐振力与z轴方向的夹角，φ是谐振力在水平面上的分量与x轴方向的夹角。

对双周期加筋薄板进行振动响应分析，假设加筋薄板的振动位移是w（x，y）exp（jωt），加强筋与板的相互作用力仅考虑法向力的作用，则周期加筋板的振动方程是（为了公式的简洁，在以下所有方程中都将省略时间因子exp（jωt））

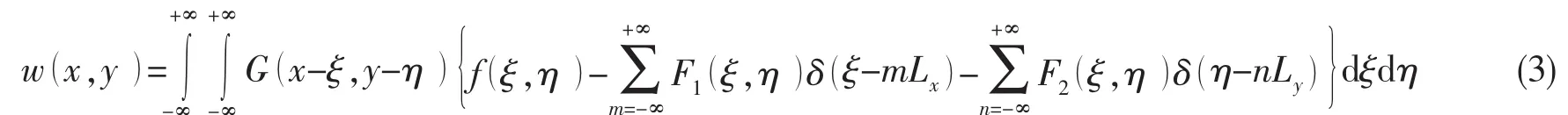
式中：G（x-ξ，y-η）是格林函数，其物理含义是：薄板由于受到作用在（ξ，η）点的单位激励力而在（x，y）位置处的振动位移。F1（ξ，η）δ（ξ-mLx）和F2（ξ，η）δ（η-nLy）是加强筋沿直线ξ=mLx和η=nLy作用于薄板的法向力。这里假设两组加强筋是完全相同的，利用薄板和加强筋的位移连续条件可以得到

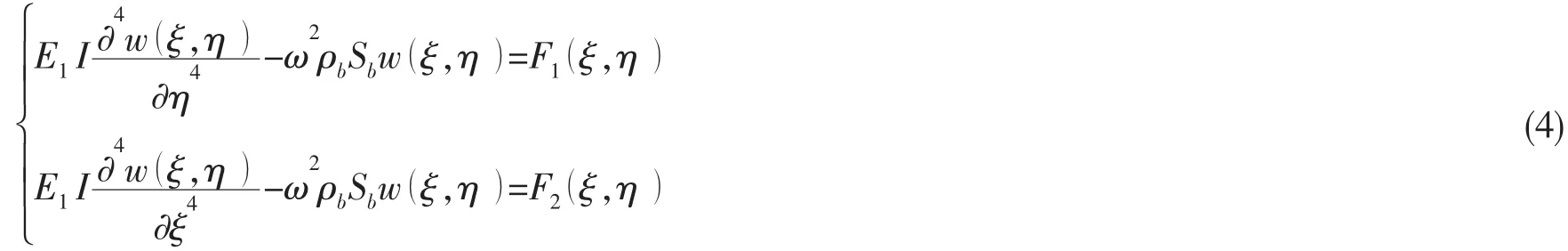
式中：E1，I，ρb，Sb分别是加强筋的杨氏模量，惯性矩，质量密度和横截面面积。

1.2 振动方程的傅里叶变换

要求解方程（3），需要对方程进行傅里叶变换。对任意满足要求的函数g（x，y），其傅里叶变换是

傅里叶逆变换是

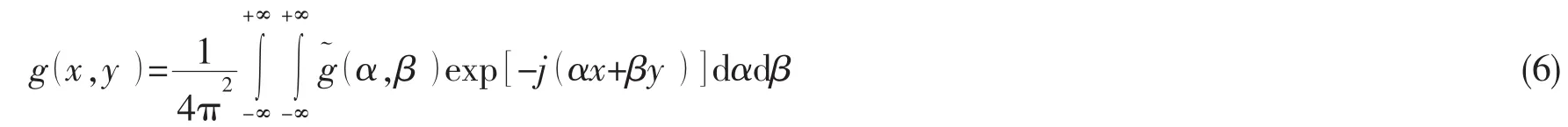
对于满足傅里叶积分定理的任意函数g1（x，y）和g2（x，y），根据函数卷积的傅里叶变换等于函数的傅里叶变换的乘积的性质可知

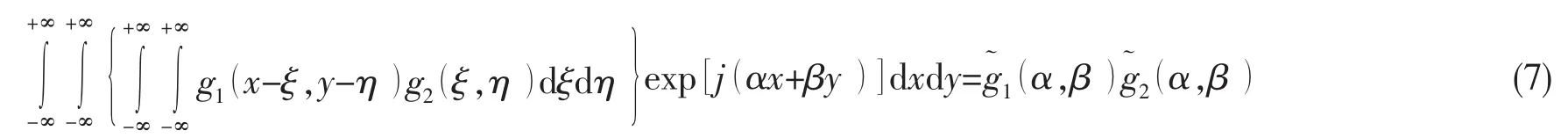
将（4）式代入（3）式中，对（3）式进行傅里叶变换，并根据（7）式的积分性质可得

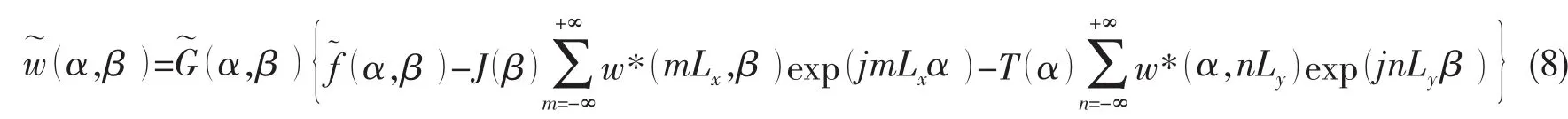
式中：w*（α，nLy），w*（mLx，β）分别是w（x，nLy），w（mLx，y）关于x轴和y轴的单重傅里叶变换，并且

流体负载下薄板的格林函数满足方程

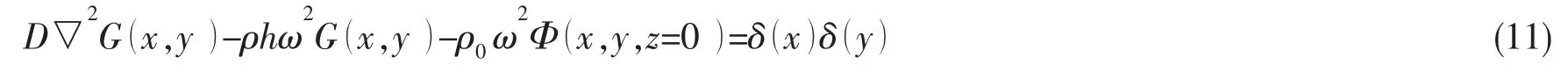
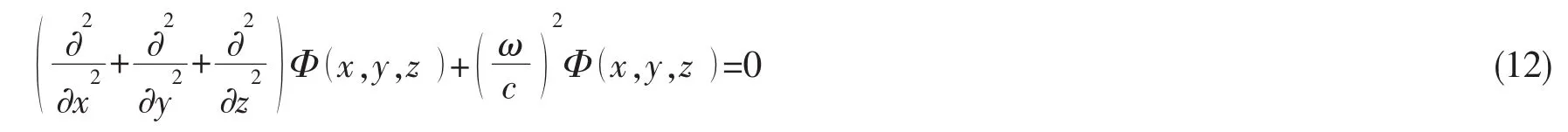
式中：c是水流体中的声速。

薄板和水流体接触面的位移边界条件是

对（12）式和（13）式进行傅里叶变换，求解得到

对（11）式进行傅里叶变换，结合（14）式可以得到频域内流固耦合的薄板阻抗

2 振动方程的求解

按照空间波数法理论[9]可知，二维周期加筋薄板的振动位移可以表达为如下形式[1]

式中：Wmn是（m，n）th谐振分量振幅，且kx，mx=kx+2mπ/Lx，ky，n=ky+2nπ/Ly。

由（16）式可以得到振动位移的周期条件

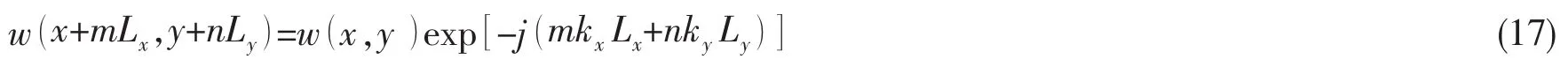
根据（17）式加筋薄板的周期条件，可知

将（18）式代入（8）式中，可得

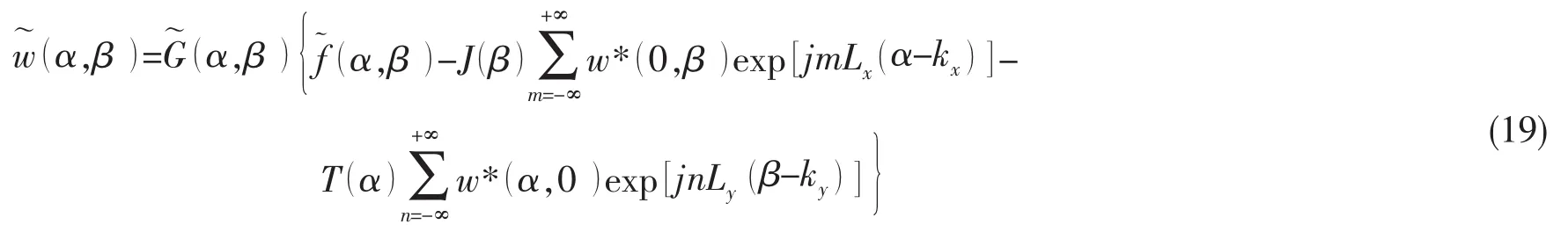
双周期加筋薄板在原点处的振动位移分别可以表达为

根据（16）式和（20）式可知，加筋薄板沿x=0和y=0直线上的振动位移分别是

对（21a）式和（21b）式分别进行关于y轴和x轴的单重傅立叶变换，得到：

由泊松迭加公式可知

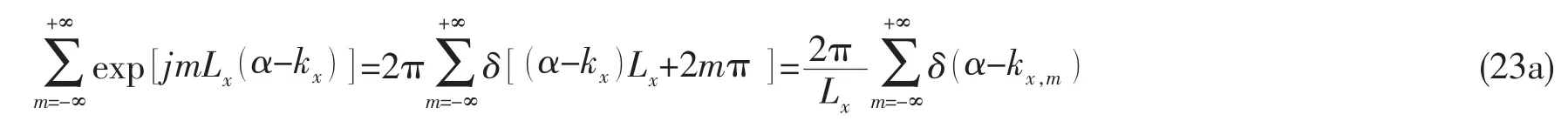
同理可得

将（9）、（22a）、（22b）式和（23a）、（23b）式代入（19）式中，可以得到频域内加筋薄板关于未知量Vn和Nm的振动方程

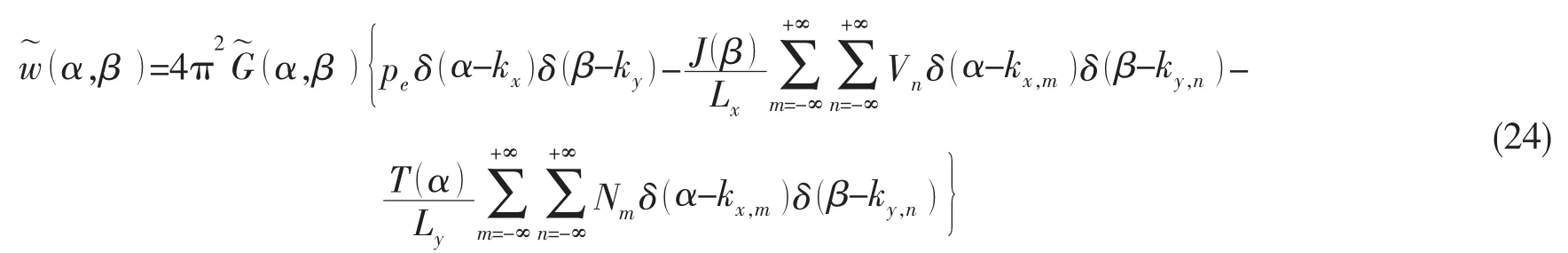
对（24）式进行关于α的单重傅立叶逆变换，并且令变量x=0以及β=ky，n，根据（22a）式得到方程[1]

同理，对（24）式进行关于β的单重傅立叶逆变换，并令变量y=0以及α=kx，m，根据（22b）式得到方程?

对（24）式进行傅立叶逆变换，最终得到时域内加筋薄板的振动方程

本文提出了无穷大双周期加筋板振动响应的格林函数法，通过比较可以发现，虽然本文与文献[1]采用的方法不同，但是本文最终求解的振动位移表达式（方程（28））和文献[1]中的表达式（方程（34））和实际物理含义是相同的，从而证明了本文方法的正确性。相对于文献[1]本文方法的优点在于：格林函数的方法不仅可以用来计算谐振面力的作用，而且可以计算包括点力激励在内的任何作用力形式；通过格林函数的应用，得到了频域内流固耦合的薄板阻抗，揭示了加强筋作用力与薄板振动位移的周期关系（（8）式）；本文中将加强筋的作用力表达为薄板振动位移的分量形式，其求解方法也与文献[1]不同。

3 计算分析

下面将利用推导的公式来计算薄板和加筋薄板的振动，并且分析加强筋对薄板振动的影响。计算中用到的部分物理参数如下：E=E1=2.01×1011×（1+0.02j），v=0.2，h=0.005，ρ=ρb=7 850，ρ0=1 000，c=1 500，pe=1 000，θ=φ=π/4，k0=ω/c。加强筋的横截面面积是Sb=0.005×0.05，短边与薄板相接。所有的单位均采用国际标准单位。本文在下面的算例分析中，通过计算发现当Q=10时，已经得到满足收敛性要求的计算精度。

图2是薄板在频率为2 000 Hz谐振力作用下，角度分别为φ=π/4和φ=π/6，在-1≤x，y≤1且时间t=0的振动响应。

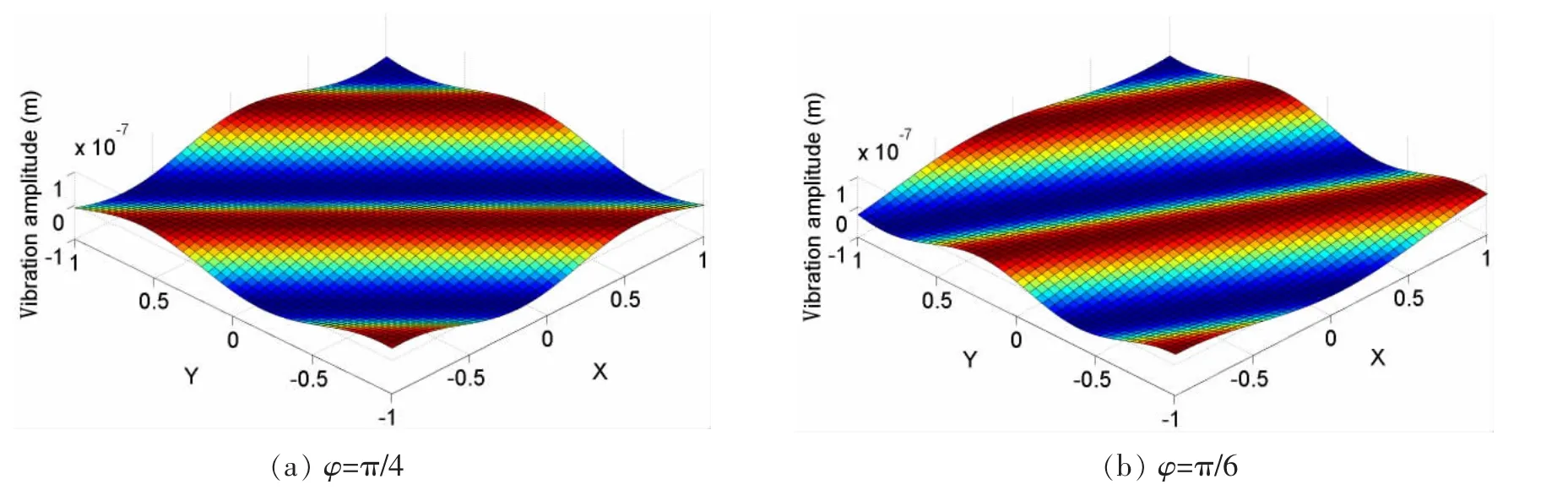
图2 薄板的振动响应Fig.2 The vibration responses of the unstiffened plate

薄板的振动特性主要取决于它的振动相位角和幅值大小。薄板的振动相位角变化方向由φ决定。从图中可以看出，当φ=π/4时，振动相位沿与x轴成45°的直线方向变化；如果改变φ的大小，如图所示，振动相位角变化方向将会随之改变。与φ不同，θ并不改变相位角变化方向，但是可以改变薄板的振动幅值大小。

图3是不同周期间距的加筋薄板在频率为2 000 Hz谐振力作用下，在-1≤x，y≤1且时间t=0的振动响应。

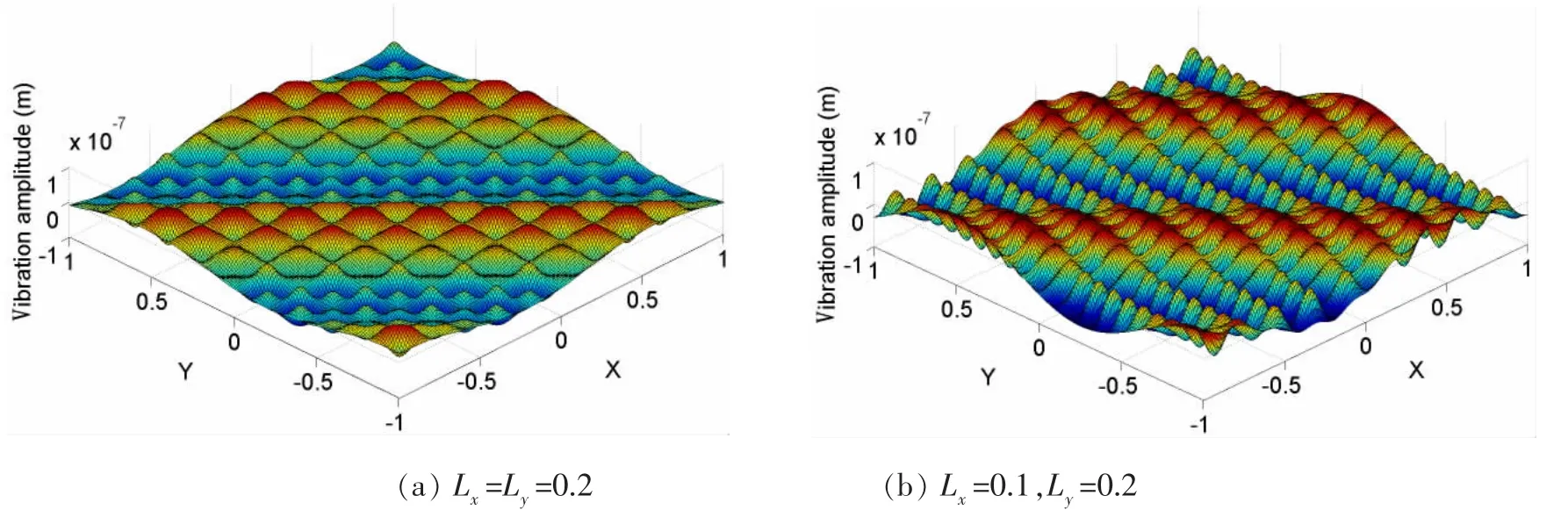
图3 加筋薄板的振动响应Fig.3 The vibration responses of the beam-stiffened plate

对比图2和图3可以发现，相对于薄板结构，双周期加筋薄板的振动具有二维周期性质，而且加筋薄板的振幅变化比较明显。从图3（a）中可以看出，加筋薄板的振动沿x轴和y轴方向上是完全一致的，这是由于沿两个轴方向的周期间距相等而且压力角φ=π/4。如果改变两轴的周期间距或压力角φ，如图3（b）所示，加筋薄板沿x轴和y轴方向的振动将不再具有对称性。

图4给出了薄板和不同周期间距加筋薄板在谐振力频率为50～2 500 Hz范围内分别在（0，0）点和（0.4，0.4）点处的振幅。周期间距分别是Lx=Ly=0.2和Lx=Ly=0.4。

从图4中可以发现，薄板在（0，0）点的振幅几乎为0，且随频率的增加不发生改变，表明在薄板中传播的振动弯曲波在通过原点位置时受到阻抑作用；在（0.4，0.4）点薄板的振幅随频率的增加而变化，振动波的传播可以顺利通过。加强筋对薄板振动的影响在100～1 300 Hz赫兹范围内作用明显，相对于薄板，加筋薄板的振幅振荡较大。随着频率的进一步增加，从整体分析，加强筋的作用减弱，加筋薄板振幅的振荡峰值减小，振幅的变化随频率的增加趋于平缓。当周期间距增大后，加筋薄板在更多的频率位置出现共振现象，表明适当增大周期间距可以增强加筋薄板的振荡效果，从而在较多的频率范围内影响薄板的振动。而且由于加强筋周期间距的增大，使得加筋薄板的共振频率向低频范围偏移，因此可以通过调节周期间距的方法改变加筋薄板的共振频率。

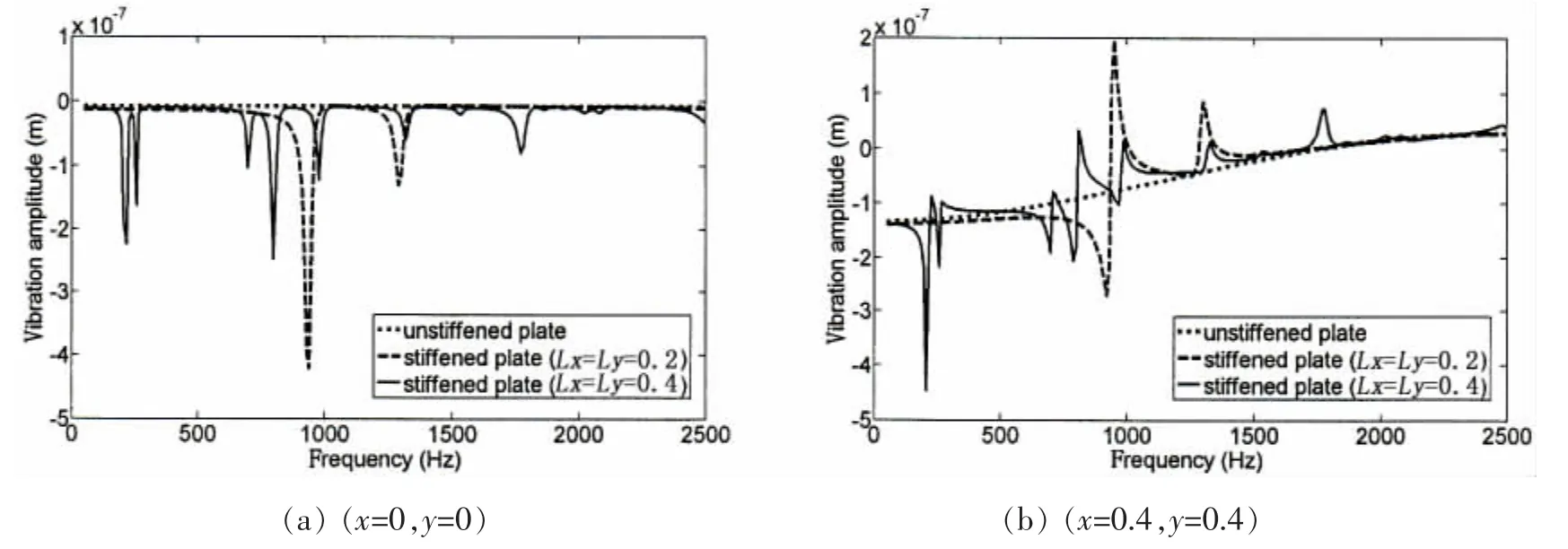
图4 在不同位置点的振动响应Fig.4 The vibration responses at different points

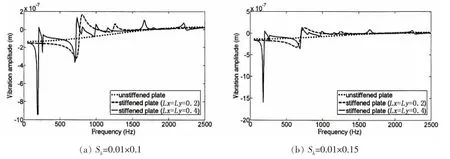
图5 不同加强筋对振幅的影响Fig.5 The influence of different beam-stiffeners on the vibration amplitudes of the stiffened plate

为了分析不同尺寸的加强筋对薄板的影响，图5给出了加强筋横截面面积分别为0.01×0.1和0.01× 0.15的周期加筋薄板在（0.4，0.4）点随频率变化的振幅曲线。

对比图5（a）和5（b）发现，增加加强筋的横截面高度对加筋薄板在200 Hz频率处的振幅影响比较明显，但对其它频率振幅的影响相对较小，而且振幅曲线在400 Hz之后随频率的增加其变化趋势是相似的。当同时改变加强筋横截面的宽度和高度尺寸后，通过对比图4（b）和5（a）可以发现，周期间距为Lx=Ly=0.4的加筋薄板的振幅曲线发生变化。从总体上分析，加强筋横截面尺寸的变化对1 000 Hz以内振动响应的作用较为显著，而对较高频率振动响应的影响较弱。

4 结论

根据格林函数和空间波数法以及傅立叶变换的应用，本文提出了一种求解受谐振力作用的流体加载下的无穷大双周期加筋薄板振动方程的方法。通过将加筋薄板的振动位移展开为波数分量迭加的形式，并采用数值计算的方法求解分量的值，从而得到了加筋薄板的振动方程表达式。在计算结果中，本文详细分析了加强筋对薄板振动响应的作用，结果表明周期加强筋对薄板的低频振动影响较大。

参考文献：

[1]Mace B R.Sound radiation from fluid loaded orthogonally stiffened plates[J].Journal of Sound and Vibration,1981,71(3): 435-441.

[2]Alain Berry.A new formulation for the vibrations and sound radiation of fluid-loaded plates with elastic boundary conditions[J].Journal of the Acoustical Society of America,1994,96(2):889-901.

[3]洪明,孙盈盈.船上含敷料板与加筋结构的固有振动特性研究[J].船舶力学,2008,12(2):311-318. Hong Ming,Sun Yingying.Natural vibration characteristics of stiffened plates and plates with covering layer in ships[J]. Journal of Ship Mechanics,2008,12(2):311-318.

[4]Lin T R,Pan J.A closed form solution for the dynamic response of finite ribbed plates[J].Journal of the Acoustical Society of America,2006,119(2):917-925.

[5]黎胜,杨婧媛.水下加筋板振动声辐射的代理模型研究[J].声学学报,2010,35(6):659-664. Li Sheng,Yang Jingyuan.Research on surrogate models for structural vibration and acoustic radiation of underwater stiffened plates[J].Acta Acustica,2010,35(6):659-664.

[6]Maxit L.Wavenumber space and physical space responses of a periodically ribbed plate to a point drive:A discrete approach[J].Applied Acoustics,2009,70(4):563-578.

[7]Mace B R.Sound radiation from a plate reinforced by two sets of parallel stiffeners[J].Journal of Sound and Vibration, 1980,71(3):435-441.

[8]陈海龙,金叶青,庞福振.一种分析单向加筋板隔声性能的解析—数值耦合法[J].船舶力学,2013,17(8):952-959. Chen Hailong,Jin Yeqing,pang Fuzhen.Sound insulation performance analysis of single stiffened plate by a combined analytical-numerical method[J].Journal of Ship Mechanics,2013,17(8):952-959.

[9]Mead D J,Pujara K K.Space harmonic analysis of periodically supported beams:Response to convected random loading [J].Journal of Sound and Vibration,1971,14(2):525-532.

[10]Lee J H,Kim J.Analysis of sound transmission through periodically stiffened panels by space-harmonic expansion method [J].Journal of Sound and Vibration,2002,251(3):349-366.

[11]吴文伟,冷文浩,沈顺根.具有等间距相同加强筋板的声辐射[J].中国造船,1999,146(3):72-81. Wu Wenwei,Leng Wenhao,Shen Shungen.Sound radiation of plate with equidistant reinforced ribs[J].Shipbuilding of China,1999,146(3):72-81.

Investigation of the vibration response of an infinite two-dimensional rib-stiffened plate under a harmonic plane pressure

ZHOU Hai-an1,WANG Xiao-ming2a,SONG Feng-min3,MEI Yu-lin2b
(1.School of Mechanical Engineering,Shandong University of Technology,Zibo 255049,China;2a.School of Mechanical Engineering;b.School of Automotive Engineering,Dalian University of Technology,Dalian 116024,China;3.Shandong Water Polytechnic,Rizhao 276826,China)

The vibration response of an infinite fluid-loaded plate,reinforced with two sets of orthogonal rib stiffeners,is investigated.The stiffeners are assumed to exert only forces on the plate.With the displacement continuity condition of the plate and the stiffeners,the vibration response of the rib-stiffened plate to a harmonic pressure in the wavenumber space is established by using the Green function and Fourier transforms.Applying the space harmonic method,the vibration displacement of the stiffened plate is then expressed as infinite sets of space harmonic amplitudes.After having a numerical solution for these amplitudes,the Fourier inverse transform is employed to find an expression for the vibration response of the stiffened plate in the physical space.Numerical results show that this method converges rapidly.

vibration response;rib-stiffened plate;Green function;space harmonic method

U661.4

A

10.3969/j.issn.1007-7294.2015.11.008

1007-7294（2015）11-1352-08

2015-07-15

国家自然科学基金资助（51405276，50875030）

周海安（1981-)，男，博士，讲师，通讯作者，E-mail：zhouhaian1981@163.com；

王晓明（1965-），男，教授，博士生导师，E-mail：xiaoming@dlut.edu.cn；

宋凤敏（1978-），女，讲师，E-mail：stj08@163.com；

梅玉林（1969-），女，副教授，E-mail：meiyulin@dlut.edu.cn。