一般边界条件下矩形薄板振动声辐射特性分析

朱理，范鑫，庞福振，缪旭弘

（1.哈尔滨工程大学船舶工程学院，哈尔滨150001；2.海军装备采购中心，北京100071；3.大连理工大学运载工程与力学学部，辽宁大连116024；4.中国人民解放军92857部队，北京100007）

一般边界条件下矩形薄板振动声辐射特性分析

朱理1，2，范鑫3，庞福振1，4，缪旭弘4

（1.哈尔滨工程大学船舶工程学院，哈尔滨150001；2.海军装备采购中心，北京100071；3.大连理工大学运载工程与力学学部，辽宁大连116024；4.中国人民解放军92857部队，北京100007）

基于改进傅立叶级数方法，将矩形板振型函数表示为包含正弦三角级数的改进傅立叶级数，从而有效地克服结构在边界处存在的不连续性，建立了一般边界条件下矩形薄板结构振动声辐射的分析方法，并对薄板结构的振动声辐射特性进行了研究。文中还建立了薄板结构的位移容许函数，然后基于最小势能原理求解了系统的Lagrange函数，最后利用Rayleigh-Ritz法对方程求解从而获得薄板自由振动的模态信息；在此基础上，基于Rayleigh积分公式推导出了薄板振动、辐射声压和声功率的表达式，研究了结构特性参数及边界条件对薄板振动声辐射的影响，通过有限元软件和参考文献的比对分析，验证了改进方法的正确性和有效性。

改进傅立叶级数；矩形薄板；振动；声辐射；容许函数

0 引言

板结构作为常见的基本结构单元，在船舶、航天等国防工业中具有广泛的应用，其动力学性能一直是研究的热点。

关于矩形薄板结构振动声辐射研究，目前已有大量研究成果，并形成了较为系统的分析方法。对于矩形薄板的动力学问题而言，归根结底就是对其控制方程和边界条件所构成的方程进行求解[1]，目前常见的分析方法有幂级数法[2]、有限板条法[3]、能量法[4]、离散奇异卷积法[5]、微分求积法[6]和Green函数法[7]。但上述研究多采用了理想边界条件[8-11]，如固支、简支、自由等典型边界条件形式进行分析的，而在实际结构工程中，结构的边界条件通常较为复杂，可能是上述典型边界条件的组合，因此，开展一般边界条件下矩形薄板结构的振动声辐射研究具有重要的现实意义。且现有文献在对矩形薄板振动声辐射的研究也大都集中于经典边界的情形[12-15]。当矩形薄板结构的边界为弹性情形时其声辐射计算要复杂得多，虽然人们在研究探索中提出了很多新的求解方法，如：Ritz法、Galerkin法、级数法和有限元法等，但是上述方法均存在各自的缺陷，如有限元法在解决结构高频振动时会出现较大误差，且结构形式或边界条件等改变时需要重新建模计算，耗时耗力。

针对现有研究存在的不足，本文基于改进傅立叶级数方法，建立了一般边界条件下矩形薄板结构的振动声辐射分析的统一模型，提出了一般边界条件下矩形薄板结构振动声辐射的快速分析方法。本文首先基于改进傅立叶级数方法建立了薄板结构横向位移容许函数，同时对系统进行能量描述；针对Lagrange函数中未知的傅立叶系数求极值得到结构振动的标准特征值方程，通过简单的数学求解得到结构的动力学特性；在此基础上，推导了矩形薄板空中辐射声压和声功率表达式，研究了在不同结构参数与边界条件下结构的振动声辐射特性；最后通过大量数值算例对所提方法进行验证，说明本文方法的正确性、合理性及有效性。

1 矩形薄板弯曲振动理论

1.1 薄板结构物理模型

本文所研究模型为一长为a，宽为b，厚为h的矩形薄板，如图1所示。板的一般边界条件可采用沿各边均匀分布的线性位移（kil，i取值为x、y，l的取值为0、a、b，在后面不再进行描述）和旋转约束弹簧（kil）来模拟。事实上，经典边界可以通过将kil和Kil设置为0或∞来模拟，例如：当将两类约束弹簧刚度值设置为∞时，则为固支边界条件；而为弹性边界时，其值可取为两极限值之间的任意值。对于边界上的线位移和旋转约束弹簧刚度的单位分别为N/m和N·m/rad。

图1 任意弹性边界下的薄板结构示意图Fig.1 Schematic of thin plate with arbitrary boundary conditions

1.2 结构控制方程的建立

由结构力学可知，法向载荷q（x，y，t）作用下薄板运动微分方程可表示为：

矩形薄板自由振动时，q（x，y，t）=0，则（1）式可简化为：

1.3 位移容许函数

在本文方法中，构造合适的位移容许函数对研究结果具有重要影响。为克服传统傅立叶级数在边界处的不连续性，一种改进的傅立叶级数表达被提了出来，并且被应用到一般弹性边界下正交各向异性矩形薄板[16]的弯曲自由振动和环扇形板[17]的面内振动分析中；本文进一步将该方法扩展到矩形薄板结构的振动与声辐射特性分析中去。

对于一般边界条件下矩形薄板结构，采用本文方法其振型函数可表示为：

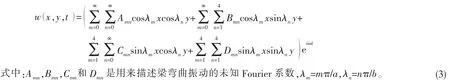
简谐时间因子eiωt的引入是为了表述薄板在不同时刻的位移函数。从上式可以看出，在求解域内，位移函数除了二维傅立叶余弦级数外还包含三项辅助傅立叶级数形式，这是由于矩形薄板的振动控制微分方程是四阶偏微分方程，因此要求它的位移容许函数要在整个求解域内三阶导数连续而且四阶导数在各点均存在。通过在传统傅立叶级数方法的基础上引入三项辅助傅立叶级数的方法使得现有的位移容许函数三阶导数在整个求解域内是连续的并且四阶导数在各点均存在，这就可有效地克服边界处可能存在的不连续性。

1.4 结构能量泛函的建立

通过对位移函数逐次求导就可以得到速度、加速度等参数，因此，整个求解过程的主要任务就是求解未知的傅立叶展开系数。在求解未知傅立叶系数时，首先对结构的能量进行描述，其具体过程如下：

矩形薄板的弯曲应变能：

储存在边界的弹簧势能可以表示为：

相应地，一般弹性边界条件下，将弹簧考虑为无质量质点，结构的整体动能为：

外载荷所做的功可以表示为：

于是，系统的Lagrange能量泛函可以表示为：

1.5 振动响应的求解

将（4）-（7）式代入（8）式，并对未知傅立叶展开系数求极值：

从而可将结构的振动问题转成了一个求解特征值方程的简单数学问题，具体表示成以下形式：

式中：［K］=［Ks］+［Kp］，［Ks］是弹簧势能刚度矩阵，［Kp］是结构应变势能刚度矩阵，［M］是结构的质量矩阵。A和F分别为相同维数的未知Fourier系数和外载荷向量。当｛F｝=｛0｝时，结构就退化为自由振动特征值方程：

当｛F｝≠｛0｝时，即任意圆频率ω激励下，结构受迫振动时的未知傅立叶系数向量可表示为：

通过将上式代入（3）式，即可得到薄板结构的受迫振动响应。

1.6 结构的声辐射

在求得薄板位移响应表达式后，声场中任意一点的声压可以通过Rayleigh积分求得：

式中：X为场点，Y为源点，ω为激励圆频率，ρ0为空气密度，c为空气中的声速，代表场点与源点间的距离。

为便于计算，将结构划分为N个有限单元，这样被离散后的结构中每个小单元都可以视为一个独立向外辐射噪声的点声源。这样（13）式可表示为：

式中：vn（Y）可以通过对位移函数wp（x，y，t）求导得到，ΔS为单元面积。

同理，借助于声强和声功率的表达式可以推导出矩形板的总辐射声功率；且当结构辐射表面与观测点所在表面重合时，可以表示成如下形式：

采用上述方法将板结构离散后，上式变为：

各离散单元中心点速度v可以表示成列向量的形式，即v=（v1，v2，v3，…，vN）T，这样辐射功率Wp可以简化为：

其中：Z为阻抗矩阵，其具体表达式如下所示，H表示共轭转置。

最终，矩形板辐射声功率级为：

2 数值计算与分析

2.1 方法的收敛性分析

因本方法在计算过程中，位移展开截断值M、N对结果具有重要影响，为此，本节首先对改进傅立叶级数方法的收敛性进行验证。

以四边固支（即C-C-C-C支撑方式）矩形薄板的自由振动为例，本节研究了截断值对无量纲固有频率的影响，计算如表1所示，其中Ω=ωa2（ρh/D）1/2。不难发现，当M=N=10时，其频率参数基本不发生变化，因此可以认为在此截断值下，改进傅立叶级数方法已收敛在后续数值计算中截断值M、N可取为10。从表中亦可看出，随着截断数的增大，薄板固有频率的计算结果趋于一致，从而证明了本文方法的数值稳定性。

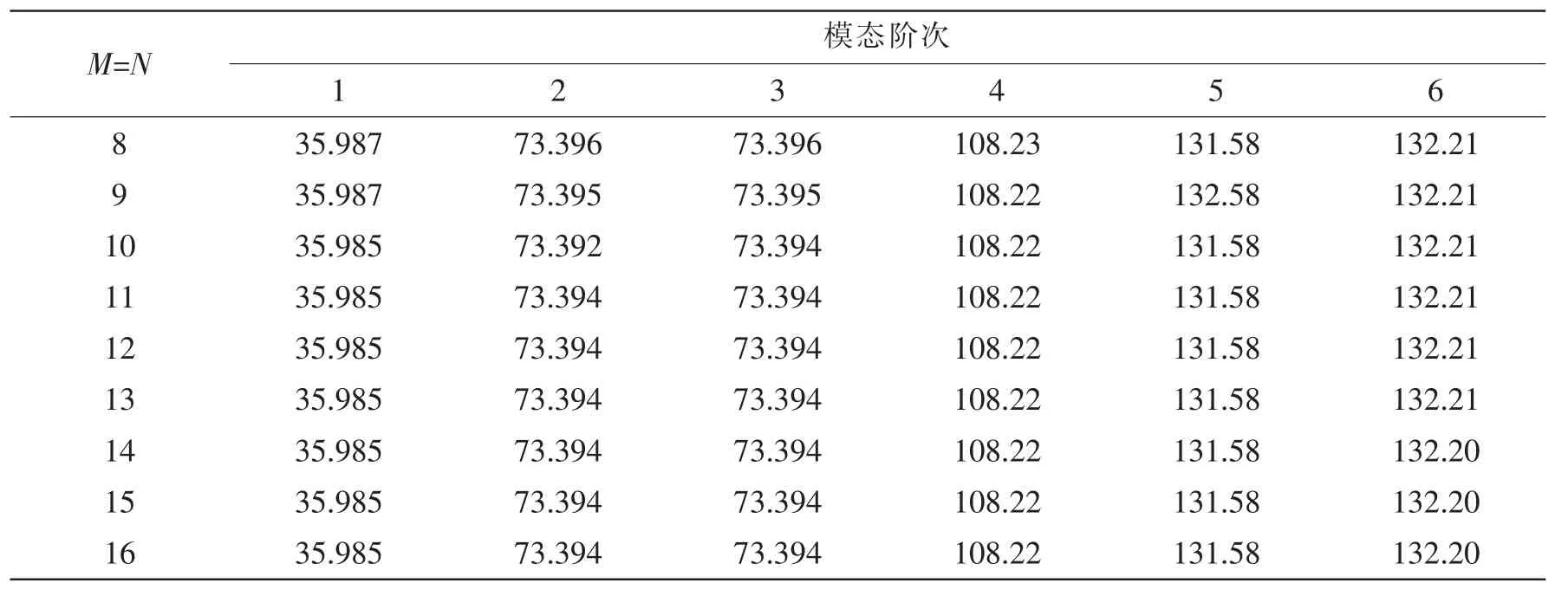
表1 不同的截断值M、N下C-C-C-C板结构无量纲频率参数ΩTab.1 Non-dimensional frequency Ω of plate with different M and N under C-C-C-C BCS

2.2 结构动力学特性分析

为了证明本方法的正确性以及对于一般边界条件的适用性，本小节对矩形薄板结构在任意边界条件下的自由振动特性进行了分析。本节选取了四种经典边界条件，即C-C-C-C、C-F-F-F、S-S-F-F和C-S-S-F，将薄板在这些条件下计算所得的无量纲频率参数Ω与有限元仿真和文献[18]计算结果进行对比，如表2至表5所示。同时，本文还列出了在C-C-C-C边界和长宽比r=2时本文方法与有限元方法计算所得的前6阶固有模态振型。通过图表数据对比可知，本文方法计算所得计算结果与现有文献解及有限元仿真结果吻合得很好，从而验证了本文方法的正确性，并且可以看出该方法具有较高的计算精度。

表2 不同的长宽比C-C-C-C板结构无量纲频率参数ΩTab.2 Non-dimensional frequency Ω of plate with different length/breadth ration with C-C-C-C BCS

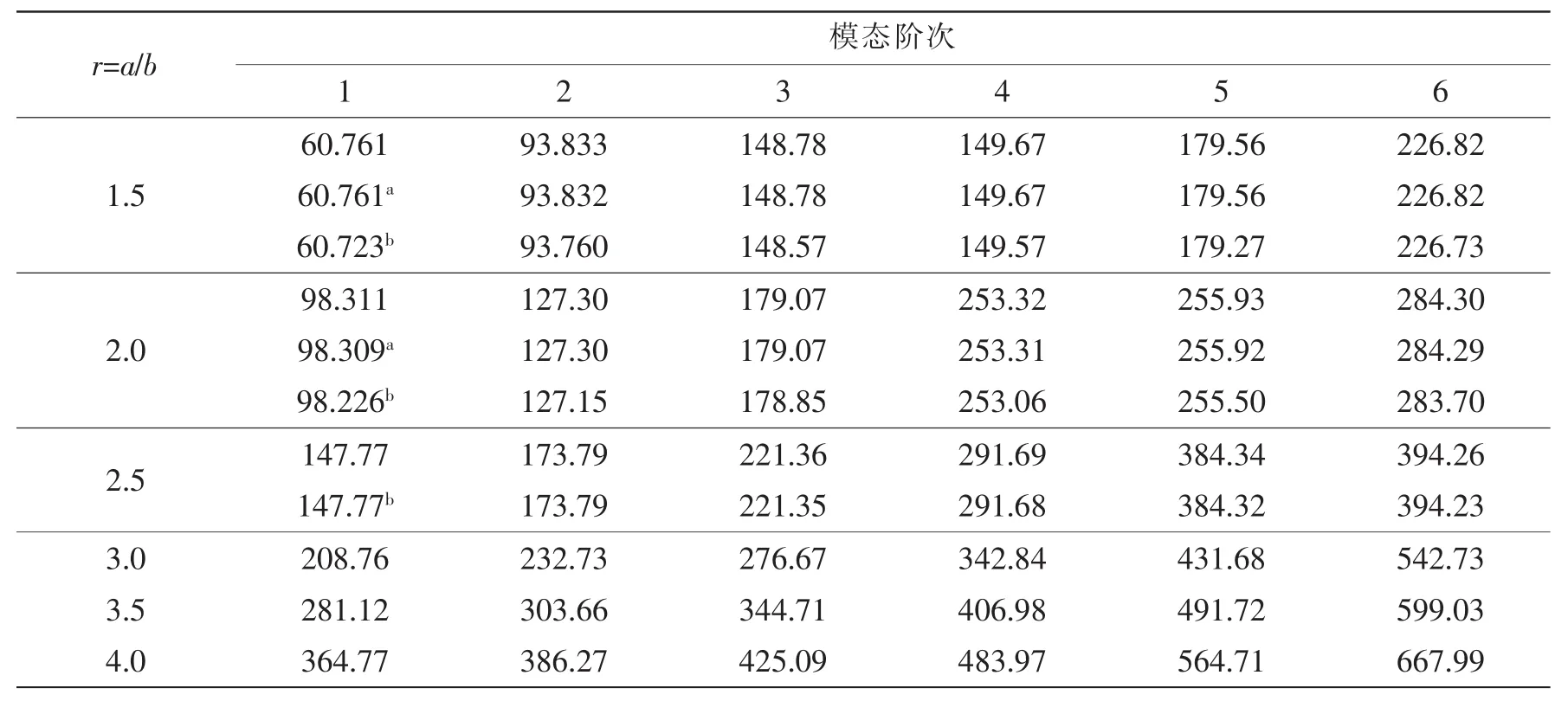
续表2

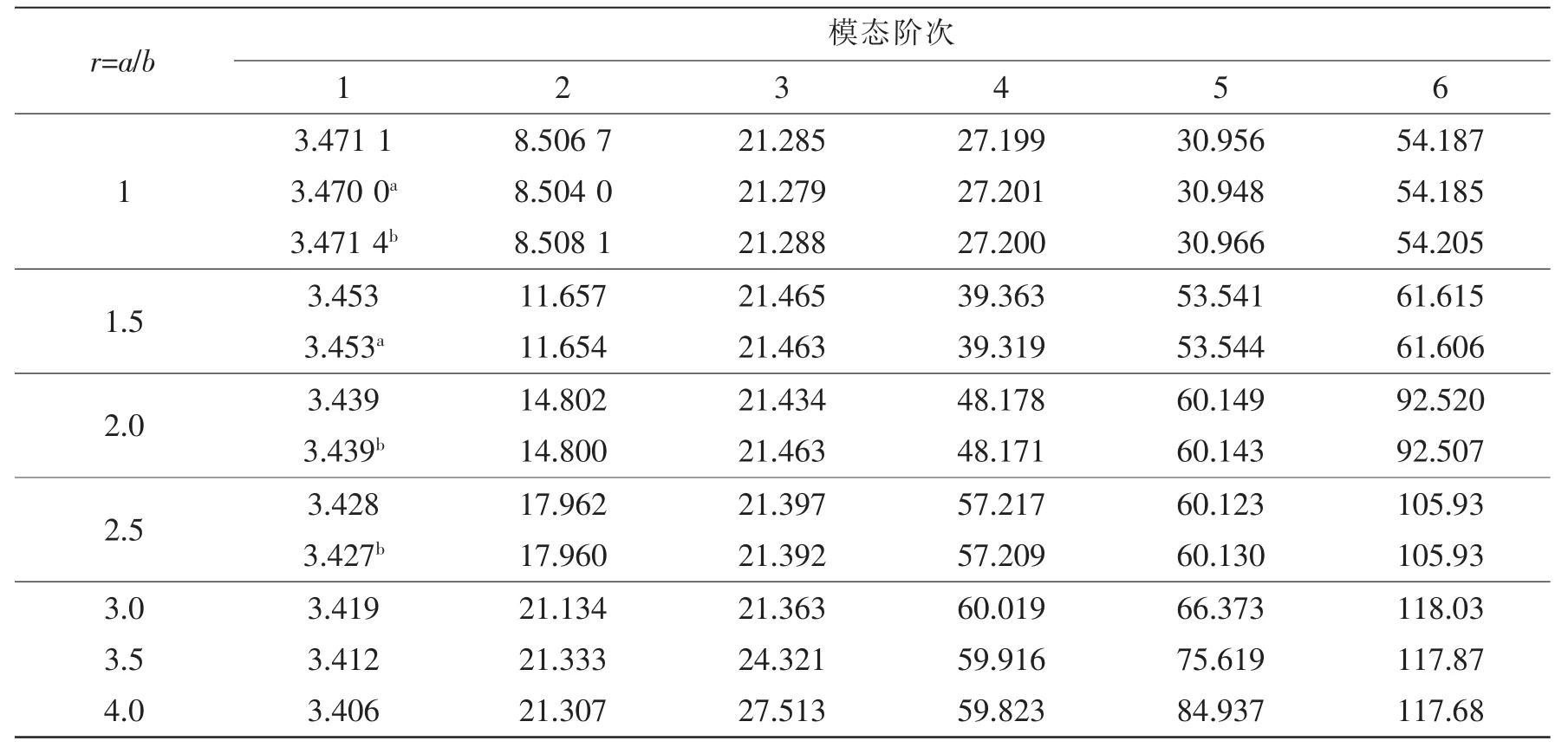
表3 不同的长宽比下C-F-F-F板结构无量纲频率参数ΩTab.3 Non-dimensional frequency Ω of plate with different length/breadth ration with C-F-F-F BCS

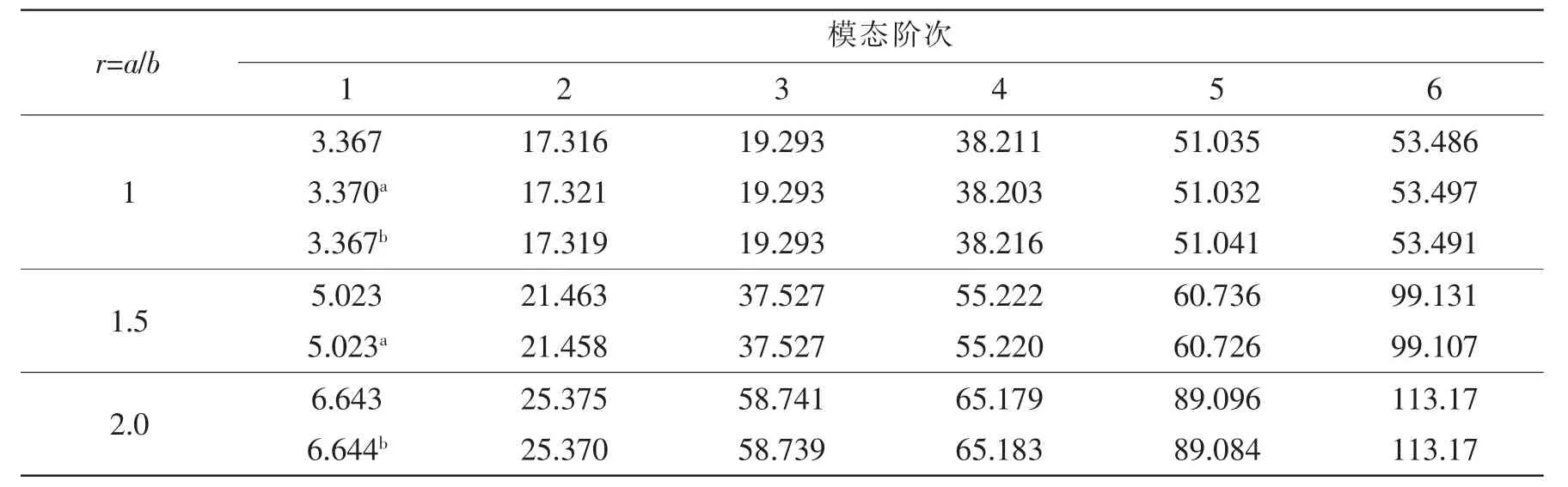
表4 不同的长宽比下S-S-F-F板结构无量纲频率参数ΩTab.4 Non-dimensional frequency Ω of plate with different length/breadth ration with S-S-F-F BCS

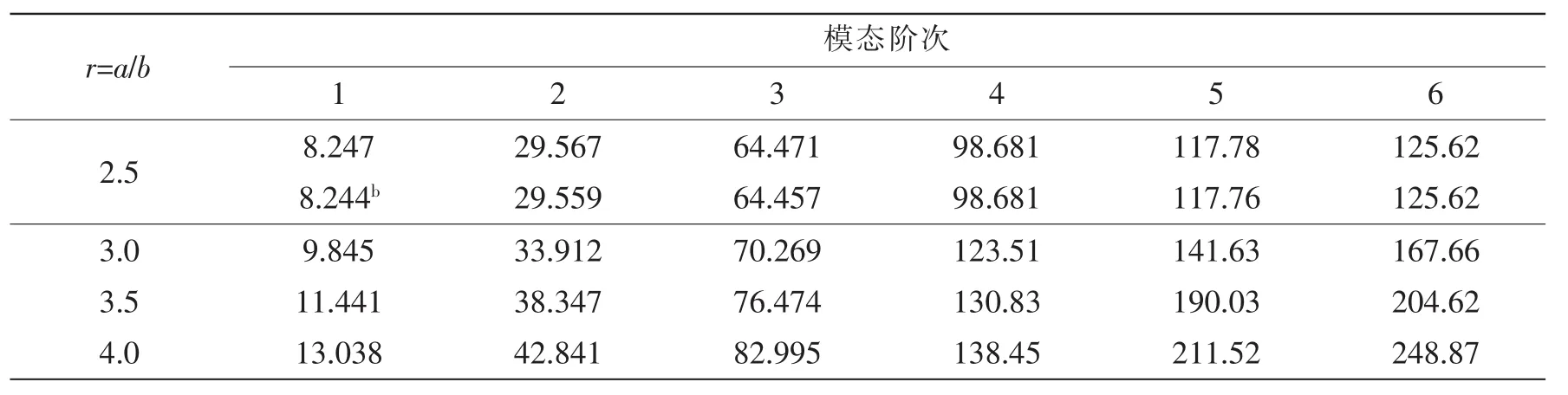
续表4

表5 不同的长宽比下C-S-S-F板结构无量纲频率参数ΩTab.5 Non-dimensional frequency Ω of plate with different length/breadth ration with C-S-S-F BCS

图2 在C-C-C-C边界下r=2时本文方法计算所得前6阶固有模态振型Fig.2 The first 6 modes of plate under C-C-C-C BCS when r=2 with proposed method

图3 在C-C-C-C边界下r=2时有限元计算所得前6阶固有模态振型Fig.3 The first 6 modes of plate under C-C-C-C BCS when r=2 with FEM

表6 S-S-S-S边界下方板在不同的旋转弹簧刚度下前6阶无量纲频率参数ΩTab.6 The first 6 Non-dimensional frequency Ω of plate with different rotating stiffness with S-S-S-S BCS

在此基础上，本文研究了一般弹性边界条件下结构的自由振动特性。表6给出了四边简支条件下同时改变四边旋转弹簧刚度值时的前6阶无量纲固有频率参数，为便于对比验证，表6同时列出了部分有限元仿真结果作为参照。从表中可以看出，本文方法计算结果与有限元仿真结果吻合得很好，这就验证了本文方法对于弹性边界的适用性。从表中还可以看出，弹性边界下的刚度值的变化对于结构的振动特性影响较大，当K的值在1×104～1×108N·m/rad区间时，结构固有频率发生剧烈变化，当K低于104N·m/rad或大于108N·m/rad时平板结构固有频率变化较小，此时结构已经退化为经典边界条件。

图4给出了C-C-C-F边界下逐渐改变F边的线性弹簧刚度k和旋转弹簧刚度K时平板结构第1阶固有频率的变化图。可以看出，当k保持不变而K在逐渐增加时，系统固有频率的曲率变化相对较小；而当K保持不变而k在逐渐增加时，图形的曲率却变化很大，由此可以断定横向约束弹簧对结构固有频率的影响比旋转弹簧大。

图4 C-C-C-F下k和K影响程度比较Fig.4 Influence of k and K with C-C-C-F BCS

2.3 平板结构振动声辐射特性研究

由于平板结构声辐射的关键在于求解给定激励下平板的速度响应，因此，对本文方法的验证最终可归结为平板结构给定激励载荷下的振动速度响应的验证上。为此，本文首先对平板结构的受迫振动响应进行分析，并通过与有限元对比验证本文方法的正确性，在此基础上，通过Rayleigh积分对平板结构在空气中的振动声辐射进行了求解，分别从边界条件、结构尺寸、板厚以及激励点位置四个方面对平板结构声辐射特性进行研究。

2.3.1 平板结构受迫振动响应分析

本节对矩形薄板结构的受迫振动速度响应进行研究。为便于分析，薄板基本参数设置如下：a=1 m，b=1 m，h=0.01 m，杨氏模量E=2.07×1011Pa，质量密度ρ=7 800 kg/m3，泊松比μ=0.3，空气中的声速c=323 m/s，空气密度ρ0=1.225 kg/m3，激励幅值为100 N，计算频率为2 Hz～1 kHz，扫频间隔为△f=2 Hz。

图5（a）和5（b）分别是在四边固支和四边简支且激励点为板中心的情况下，分别利用本方法和有限元软件计算所得的中心点和（0.2，0.3）点处的速度响应级对比图。由图可知，本文方法求解得到的速度响应与有限元软件计算结果吻合得很好，只是在两个共振的峰值点上出现了部分的差异，这是由于不同方法对于同一结构共振峰的测定有一定的差异。因而，可以断定：本文方法在对结构声辐射方面的计算结果是正确可靠的。

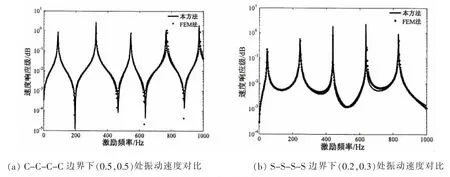
图5 平板振动速度响应对比图Fig.5 Vibration velocity of plate with different BCS

2.3.2 平板结构声辐射研究

下面将分别从边界条件、结构尺寸、板厚以及激励点位置四个方面因素对薄板结构振动声辐射的影响进行研究。

（1）边界条件对结构声辐射的影响

图6给出了C-C-C-C﹑C-F-F-C和C-S-S-F三种不同边界条件下平板结构辐射声压级与声功率级比较图，其中声压级监测点位于平板中心上方0.1 m处的位置。

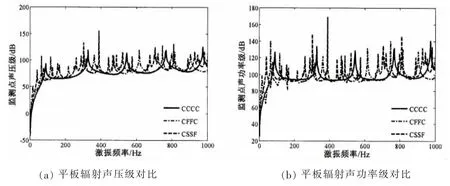
图6 典型界条件下结构声压与声功率对比Fig.6 Comparison of sound pressure and power of plate with different BCS

由图6可以看出，一方面，在共振频率处，不论是平板的辐射声压还是辐射声功率均呈现出了峰值，这说明无论边界条件如何变化，只要激励频率与结构固有频率相等，均会有共振的情形出现；另一方面，对比不同边界条件下平板辐射声压级与辐射声功率级曲线可以看出，C-C-C-C边界条件时平板结构声辐射共振峰最少，C-F-F-C边界条件次之，C-S-S-F边界条件时最为密集，由此可见，随着结构边界约束条件的减弱，结构声压级与辐射声功率级共振峰也更为密集，辐射能量也更大，可见，边界条件对结构声辐射的影响较大，增强结构的边界约束条件可有效降低结构的声辐射。

图7给出了旋转约束弹簧刚度值K＝1×105N·m/rad不变而横向约束弹簧刚度值k分别为2×104N/m、2×105N/m和2×106N/m时平板结构辐射声压级与声功率级的对比曲线。可以看出，随着横向约束弹簧刚度k的增加，其结构声辐射响应峰值点在向高频移动，而且从第一个峰值点的对比可以看出，横向约束弹簧刚度k越大，其响应峰值点也越高。此外，对比图6与图7可知，与经典边界不同的是：①弹性边界下高频峰值点趋于相同位置只是峰值点的值有所不同；②弹性边界下平板结构辐射声功率除峰值点外还会出现一段平稳过程，而经典条件下几乎不会出现或者说出现的频率段范围很小。

图7 典型横向约束刚度下结构声压与声功率对比Fig.7 Comparison of sound pressure and power of plate with typical transverse constraint stiffness

（2）结构长宽比对声辐射的影响

图8给出了a/b=1﹑1.5和2等三种不同长宽比下四边固支时平板结构辐射声压级与声功率级的对比曲线。

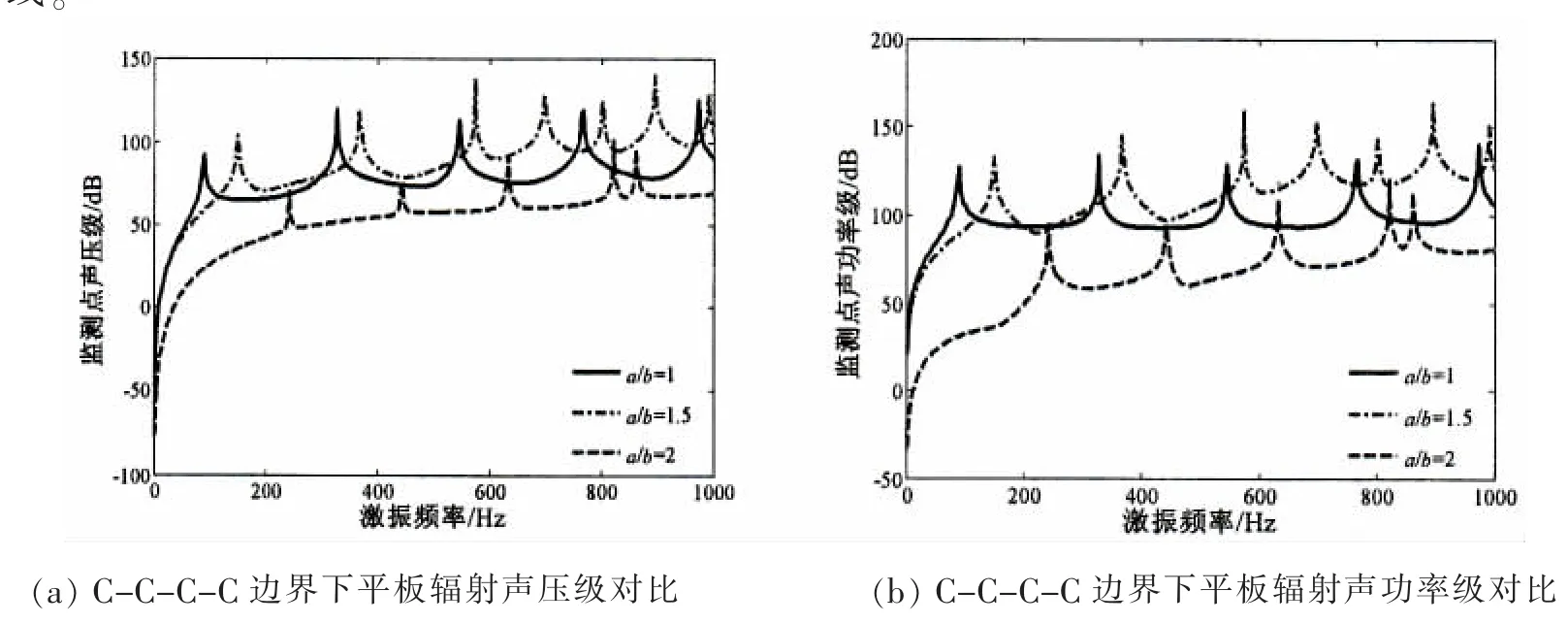
图8 典型尺寸下结构声压与声功率对比Fig.8 Comparison of sound pressure and power of plate with different size of plate

可以看出，一方面，随着长宽比的增加，平板结构声辐射共振峰值将逐渐向高频段偏移，且共振峰数量也将存在较大差异，a/b=1.5时，结构声辐射共振峰最多，a/b=1时次之，a/b=2时最少；另一方面，随着长宽比的增加，结构辐射声压和辐射声功率也将发生改变，对于本文研究的平板结构而言，a/b=1.5时平板结构辐射噪声最大，a/b=1时次之，a/b=2时平板结构振动声辐射水平最低。

（3）板厚对结构声辐射的影响

图9分别给出了h=0.005 m﹑0.01 m和0.015 m三种不同板厚下四边固支板结构振动声压级与声功率级比较曲线。从图中可以看出，随着板厚的增加，一方面第1阶声辐射共振峰频率在逐渐提高，且其1阶共振时峰值也在增大；另一方面，随着结构板厚的增加，平板结构声辐射共振峰数量在逐渐减少。

图9 典型板厚下结构声压与声功率对比Fig.9 Comparison of sound pressure and power of plate with different thickness of plate

（4）激励点位置的影响

图10给出了激励点在（0.3，0.3）﹑（0.4，0.4）和（0.5，0.5）三种不同位置下四边固支板结构振动声压级与声功率级的比较曲线。可以看出，激励点位置的改变对平板结构声辐射的影响相对较小，且由于此时结构自身的动力学特性不发生变化，而激励作用点位置的改变仅会引起结构被激励模态的变化，因此其声辐射响应变化不大。对于本次研究的平板结构而言，无论激励点在何处，其首阶共振峰位置是相同的；但当激励点作用于结构中心位置时，结构的反对称模态将无法被激起，故其声辐射共振峰值数目较少；而当激励点不再对称中心时，结构的反对称模态也将被激起，故此时结构的辐射声压和声功率会不断增大，且其共振峰数量也相对较多。

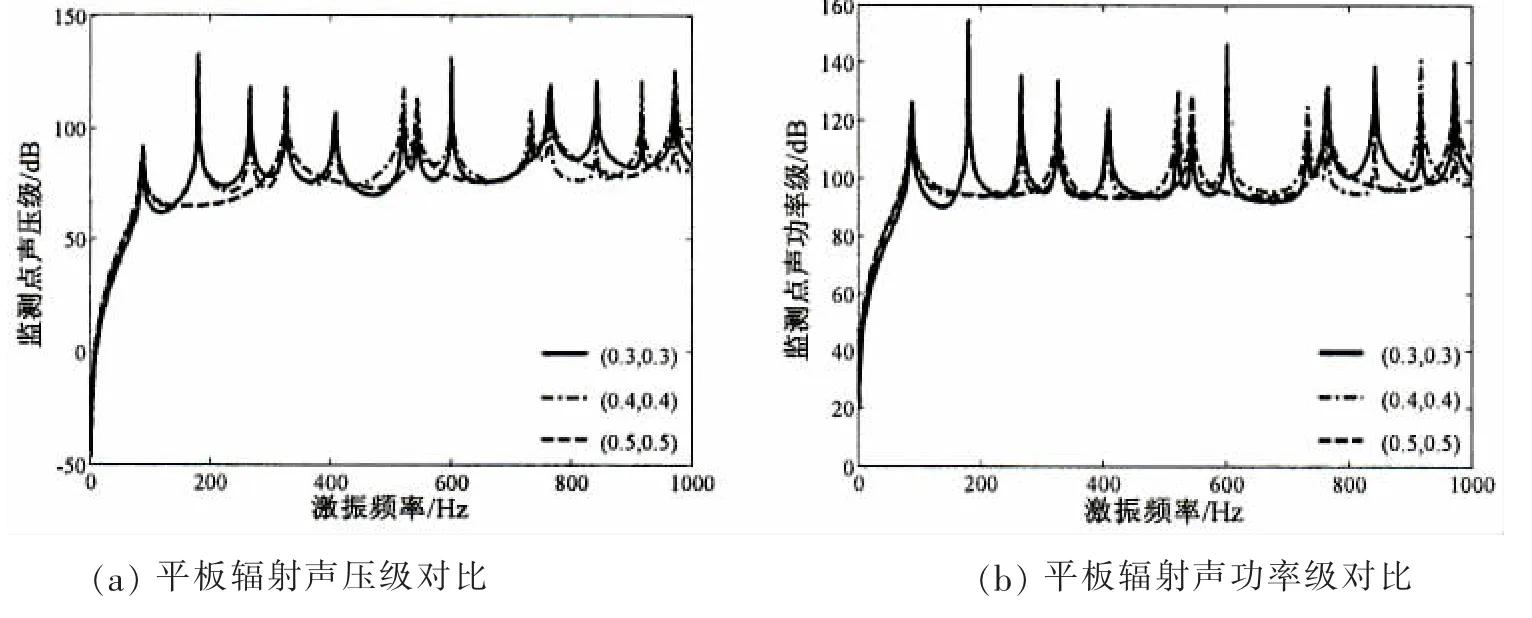
图10 典型激励位置下结构声压与声功率对比Fig.10 Comparison of sound pressure and power of plate with different size of plate

3 结论

本文基于改进傅立叶级数方法建立了一般边界条件下矩形板振动声辐射的分析模型。在对结构进行能量描述的基础上建立了Lagrange函数，通过将未知傅立叶系数作为广义变量，结合Rayleigh-Ritz法将结构振动问题转化为求解标准特征值方程的问题；在此基础上，结合Rayleigh积分进一步导出了任意边界下薄板结构的辐射声压和声功率表达式，并讨论了不同参量对于结构声辐射的具体影响。通过上述研究可以得出如下结论：

（1）改进傅立叶级数方法分析平板结构振动声辐射问题是可行的，且具有计算精度高、数值稳定性好等优点。

（2）薄板结构动力学特性分析表明，横向约束弹簧对结构固有频率的影响比旋转弹簧大。

（3）薄板结构声辐射特性研究表明，边界条件、长宽比、板厚、激励点位置等会对结构声辐射产生影响：当激励频率与结构第1阶固有频率相等时，一般会引起结构共振声辐射情形的出现，且随着边界约束条件的减弱，共振声辐射逐渐增多且峰值越来越大；随着长宽比和板厚的增加，结构振动首个共振峰的位置在逐渐向高频范围移动，结构共振峰数量在逐渐减少；激励点位置不改变结构共振频率，但可能因无法激励结构局部共振模态而导致其声辐射共振峰的减少。

[1]薛开,王久法,王威远.变厚度薄板在任意弹性边界条件下的自由振动分析[J].振动与冲击,2013,32(21):131-135. Xue Kai,Wang Jiufa,Wang Weiyuan,Li Qiuhong，Wang Ping.Free vibration analysis of tapered plates with arbitrary elastic boundary condition[J].Journal of Vibration and shock,2013,32(21):131-135.

[2]Sakiyama T,Huang M.Free vibration analysis of rectangular plates with variable thickness[J].Journal of Sound and Vibration,1998,216(3):379-397.

[3]苏淑兰,饶秋华,王银邦.单向变厚度Levy型薄板的自由振动分析[J].中南大学学报(自然科学版),2011,42(5): 1413-1418. Su Shulan,Rao Qiuhua,Wang Yinbang.Free vibration of Levy-plate with uni-directionally varying thickness[J].Journal of Central South University(Science and Technology),2011,42(5):1413-1418.

[4]Cheung Y K,Zhou D.The free vibration of tapered rectangular plates using a new set of beam with the Rayleigh-Ritz method [J].Journal of Sound and Vibration,1999,223(5):703-722.

[5]Malekzadeh P,Karami G.Large amplitude flexural vibration analysis of tapered plates with edges elastically restrained against rotation using DQM[J].Engineering Structures,2008,30(10):2850-2858.

[6]Bert C W,Malik M.Free vibration analysis of tapered rectangular plates by differential quadrature method:A semi-analytical approach[J].Journal of Sound and Vibration,1996,190(1):41-63.

[7]Kobayashi H,Sonoda K.Vibration and buckling of tapered rectangular plates with two edges simply supported and the other two edges elastically restrained against rotation[J].Journal of Sound and Vibration,1991,146(2):323-337.

[8]Leissa A W.The free vibration of rectangular plates[J].Journal of Sound and Vibration,1973,31,257-293.

[9]Bhat R B.Natural frequencies of rectangular plates are obtained by employing a set of beam characteristic orthogonal polynomials in the Rayleigh-Ritz method[J].Journal of Sound and Vibration,1985,102(4):493-499.

[10]Chen H L.Exact solutions for free-vibration analysis of rectangular plates using bessel function[J].Journal of Applied Mechanics,2007,74(2):1247-1251.

[11]Zhou Ding.Natural frequencies of rectangular plates using a set of static beam functions in rayleigh-ritz method[J].Journal of Sound and Vibration,1996,189(1):81-87.

[12]任惠娟,盛美萍.矩形薄板的模态声辐射效率[J].机械科学与技术,2010,29(10):1397-1400. Ren Huijuan,Sheng Meiping.A thin rectangular plate’s modal radiation efficiency[J].Mechanical Science and Technology for Aerospace Engineering,2010,29(10):1397-1400.

[13]尹岗,陈花玲,陈天宁.薄板低频声辐射效率的研究[J].西安交通大学学报,1999,33(3):108-110. Yin Gang,Chen Hualing,Chen Tian ning.Acoustic radiation efficiency of thin plate at low frequency band[J].Journal of Xi’an Jiaotong University,1999,33(3):108-110.

[14]Graham R.High frequency vibration and acoustic radiation of fluid loaded plates[J].Transactions of Royal Society,London,1995,A 352:1-43.

[15]Li W L,Gibelings H J.Determination of the mutual radiation resistances of a rectangular plate and their impact on the radiated sound power[J].Journal of Sound and Vibration,2000,229(5),1213-1233.

[16]史冬岩,王青山,石先杰,庄重.任意边界条件下正交各向异性薄板自由振动特性分析[J].上海交通大学学报, 2014,48(3):434-438. Shi Dongyan,Wang Qingshan,Shi Xianjie,Zhuang Zhong.Free vibration analysis of orthoropic think plates in general boundary condictions[J]Journal of Shanghai Jiaotong University,2014,48(3):434-438.

[17]史冬岩,石先杰,李文龙.任意边界条件下环扇形板面内振动特性分析[J].振动工程学报,2014,27(2):1-8. Shi Dongyan,Shi Xianjie,Li Wenlong.In-plane vibration analysis of annular sector plates with arbitrary boundary supports [J].Journal of Vibration Engineering,2014,27(2):1-8.

[18]Li Wenglong,Zhang Xuefeng,Du Jingtao,Liu Zhigang.An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports[J].Journal of Sound and Vibration,2009,321(1-2):254-269.

Analysis of vibration and acoustic radiation characteristics for rectangular plates with general boundary conditions

ZHU Li1,2,FAN Xin3,PANF Fu-zhen1,4,MIAO Xu-hong4
(1.College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China;2.Navy Armament Merchant Center,Beijing 100071,China;3.Faculty of Vehicle Engineering and Mechanics,Dalian University of Technology,Dalian 116024,China；4.92857Army of PLA,Beijing 100007,China)

Based on the theory of plates,a new method called Improved Fourier Series Method(IFSM)is presented to study the vibration and acoustic characteristics of rectangular plates with arbitrary boundary conditions.The plate admissible functions is presented,which is invariantly sought as an improved Fourier cosine series,and a sine series is introduced to overcome the discontinuities of the structure.And then the Lagrange equation is established according to the principle of the minimum potential energy.Finally,by using the Rayleigh-Ritz technique the vibration characteristics can be easily acquired.Under these circumstances,with the help of Rayleigh integral formula,the expressions of sound pressure and acoustic power are derived.The effects of structural parameters and boundary conditions that have great impact on the acoustic radiation are also studied.The comparisons among numerical simulation results,which obtained with FEM and reposed in literatures,validate the correctness of the method．

improved Fourier series;rectangular plates;vibration;acoustic radiation;admissible function

O342TB532

A

10.3969/j.issn.1007-7294.2015.11.014

1007-7294（2015）11-1409-13

2015-05-12

国家自然科学基金项目（51209052）；黑龙江省青年科学基金资助项目（QC2011C013）；哈尔滨市科技创新人才研究专项资金项目（2011RFQXG021）；上海交通大学海洋工程国家重点实验室基金（1307）；中国博士后基金（2014M552661）

朱理（1983-），男，博士研究生；

范鑫（1991―），男，本科生；

庞福振（1980―），男，博士后，副教授，E-mail：pangfuzhen@hrbeu.edu.cn。